基于Exp-ln模型与广义黏弹性理论的橡胶本构模型及其应用研究

基于Exp-ln模型与广义黏弹性理论的橡胶本构模型及其应用研究

仲健林，任杰,马大为

(南京理工大学机械工程学院，南京210094)

摘要：提出了一种描述橡胶材料不同应变率下力学响应的黏超弹本构模型。首先，利用Instron实验机和SHTB实验装置，开展橡胶材料单轴拉伸实验；其次，结合Exp-ln超弹性本构模型和广义黏弹性方法，建立了橡胶材料黏超弹本构模型；再次，推导本构模型三维增量格式，编写了用户子程序(VUMAT)，验证了本构模型的一维和三维有效性；最后，建立橡胶底座冲击附加载荷计算数值模型，并将冲击附加载荷实验与数值仿真进行对比验证。结果表明：单轴拉伸实验与数值解吻合较好，冲击附加载荷实验值与仿真值误差约为7%，验证了黏超弹本构模型的正确性。

关键词：橡胶材料；热黏超弹性；拉伸实验；材料子程序(VUMAT);橡胶底座

中图分类号:TJ762.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.024

Abstract:A visco-hyperelastic constitutive model was proposed to describe mechanical responses of rubber material under different strain rates. Firstly, the uniaxial tensile tests for rubber material were conducted with Instron testing machines and SHTB testing devices. Secondly, combined with Exp-ln hyperelastic constitutive model and the generalized viscoelastic method, the visco-hyperelastic constitutive model for rubber material was built. Thirdly, the three-dimensional incremental format of the visco-hyperelastic constitutive model was deduced, the user subroutine VUMAT was written, the one-dimensional effectiveness and three-dimensional one were verified. Finally, the impact additional load numerical simulation model of a rubber base was established, the results of impact additional load tests were compared with those of the numerical simulation. The results showed that the numerical results agree well with the uniaxial tensile test data, the error between the impact additional load test value and the simulation one is approximately 7%, the correctness of the visco-hyperelastic constitutive model is verified.

Constitutive model and its application for rubber material based on Exp-ln model and generalized viscoelastic theory

ZHONGJian-lin,RENJie,MADa-wei(School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094, China)

Key words:rubber material; visco-hyperelastic constitutive model; tensile test; VUMAT; rubber base

橡胶是由重复单元(链节)构成的长链分子，常用作橡胶底座等复合材料制品的基体材料[1]。从本质上说橡胶是一种黏弹性材料，力学特性与应变率有关[2-3]。在准静态条件下，橡胶的蠕变柔量或松弛模量为常数，橡胶表现为超弹特性，因此，橡胶材料的本构研究包括超弹性和黏弹性。Yang等[4-6]基于Yeoh函数提出了橡胶类材料的黏超弹本构模型并将其应用于冲击仿真。Antoun[7-9]将本构方程表示为与坐标系无关的形式，提出了描述橡胶类材料黏弹性的本构模型。在小应变范围内(<30%)，上述本构模型的预测结果与实验数据吻合较好，但由于本构建模过程中引入了由应变不变量组成的多项式，参数较多且物理含义不明确，可能会出现多解状况[10]。因此，构建一种预测应变范围大、参数少且物理含义明确的黏超弹本构模型其意义显而易见。

文中利用Instron实验机和SHTB实验装置，获得了不同应变率下的橡胶材料拉伸应力-应变曲线；建立了橡胶材料黏超弹本构模型，超弹性本构采用参数较少且物理意义明确Exp-ln应变能函数描述，黏弹性本构建立在应变、时间效应解耦的基础上，避免了引入应变不变量多项式；拟合了黏超弹本构相关参数，推导了本构模型的三维增量格式，编写了本构模型的用户子程序，将单轴拉伸、圆筒扭转实验分别与数值解进行对比验证；应用该本构模型的用户子程序完成橡胶底座冲击附加载荷计算数值模型的建立，并将冲击附加载荷实验与数值仿真结果进行对比验证。研究方法可为橡胶材料力学特性研究提供参考。

1不同应变率下的拉伸实验

常见的获取材料参数的实验方法包括:单轴拉伸(压缩)、双轴拉伸和平面剪切等，单轴拉伸实验方法简单、满足理论研究需要。针对橡胶材料，开展不同应变率下的单轴拉伸实验，获得应力-应变曲线，为黏超弹本构的参数拟合提供依据。

1.1橡胶材料单轴拉伸实验

图1　橡胶试件 Fig.1 rubbertest specimen

1.2实验结果与分析

整理数据采集系统得到的信号，得到不同应变率下的工程应力P11-工程应变ξ11，见图2。

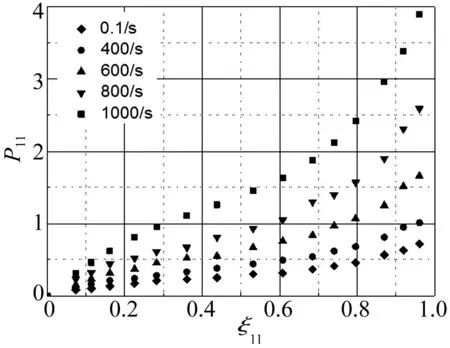
图2　不同应变率下拉伸实验应力-应变曲线 Fig.2 Stress-strain curves of the tensile test under strain rate

由图2可知，橡胶试件的应力随应变的增大而增大；随应变率的增大，橡胶试件的应力增大。橡胶材料的力学响应表现出明显的应变率敏感性。

2橡胶材料黏超弹本构模型

橡胶材料黏超弹本构关系中包含率无关的超弹性应力σe和率相关的黏弹性应力σv。将超弹性本构模型与黏弹性本构模型进行组合，建立了橡胶材料黏超弹本构模型。

2.1Exp-ln超弹性本构模型

(1)

超弹性材料的应力应变关系可以用应变能函数W来度量，根据能量守恒可得，各向同性不可压缩橡胶材料的本构方程为

(2)

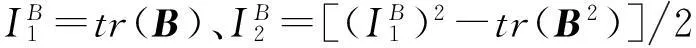
常见的应变能函数W有：Yeoh应变能函数、Mooney-Rivilin应变能函数等。文献[4]结合Mooney-Rivilin应变能函数给出橡胶材料的黏超弹本构模型，但是该模型需拟合的参数较多且预测的应变范围有限。采用参数具有实际物理意义且适用应变范围较广的Exp-ln应变能函数，该应变能函数[11]为

(3)

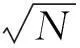
(4)

(5)

(6)

2.2基于广义黏弹性方法的黏超弹本构模型

目前，常见的黏弹性本构描述是将其表示为与坐标系无关的形式，使用应变不变量的多项式表示应变历史对应力影响的张量泛函，多项式参数较多，物理意义不明确。本文结合Gamonpilas[12]给出的广义黏弹性本构模型的描述方法，将应变ξ和时间t对应力的影响效应进行解耦，避免了引入多项式，黏超弹本构模型为

σ(ξ,t)=σ0(ξ)g(t)=σe+σv=

(7)

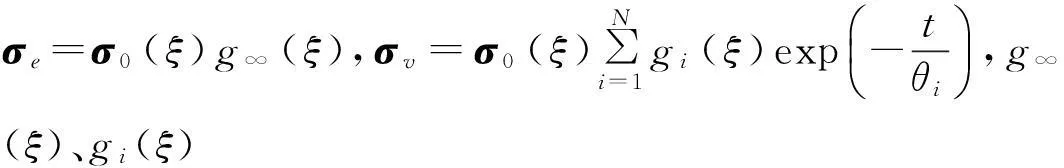
积分形式的本构方程能直接反映黏弹性材料的记忆特性，结合Leaderman卷积积分[13]和式(7)，橡胶材料黏超弹性本构为

(8)

将式(8)分解为超弹性应力部分和黏弹性应力部分，三维全量格式黏超弹本构模型为

σ=σe+σv=σ0(ξ)g∞(ξ)+

(9)

(10)

假设加载前材料的应力状态不影响加载后的应力状态，即时间积分下限为零，为减少模型参数数量，取一个松弛时间(N=1)，联立式(9)、(10)可得

(11)

(12)

(13)

(14)

b′ln(λ2+2λ-1-2)]

(15)

通过式(15)结合动态单轴拉伸实验数据，在求得两个超弹性参数a,b的值的基础上，利用最小二乘法拟合确定三个黏弹性参数A′,a′,b′和松弛时间θ1的值。文中橡胶的应变率跨越3个数量级，而橡胶的力学行为与高应变率、低应变率有关。本研究中取N=1，仅通过一个松弛时间来描述橡胶材料在整个应变率范围的力学行为，可能会造成描述的误差，有待进一步考证。

3本构模型的数值验证

3.1黏超弹本构的参数拟合

将橡胶材料单轴拉伸实验数据代入黏超弹本构模型中，进行最小二乘法拟合，即可获得本构模型的6个待定参数，参数拟合步骤为

步骤1 根据准静态加载条件下橡胶材料单轴拉伸实验数据，结合式(6)并采用最小二乘法确定两个超弹性参数a,b的值。

步骤2 将a,b代入式(15)中，选取应变率为1000s-1的曲线进行非线性拟合，确定三个黏弹性参数A′,a′,b′和松弛时间θ1的值。至此橡胶材料黏超弹本构模型中所有参数全部求得，见表1。

表1　黏超弹本构模型参数值

3.2本构模型三维增量格式与VUMAT开发

为进行VUMAT子程序开发，需对式(9)三维全量格式本构进行有限元离散，建立三维应力增量与应变增量之间的关系。

(17)

(18)

又

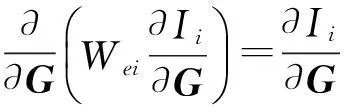
(19)

由式(17)得

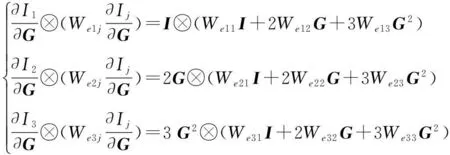
dS=DijkldE

(21)

结合式(18)和式(20)，即可给出

Dijkl=4[We11δjiδlk+2We12δjigkl+3We13δjigkmgml+

2We21gijδlk+4We22gijgkl+6We23gijgkmgml+3We31gimgmjδlk+

6We32gimgmjδlk+6We32gimgmjgkl+9We33gimgmjgkngnl+

2We2δkiδlj+3We3(δkiglj+gikδli)]

(22)

将式(3)应变能函数We代入式(22)求得切线本构张量Dijklei，通过编制VUMAT子程序获得Kirchhoff应力张量S和Green应变张量E的更新，对于不可压缩橡胶有σe=FSFT、E=1/2(FTF-ξ)，即可获得超弹本构模型σe的应力更新。

(23)

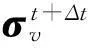
(24)

对于式(24)采用分步积分，第一部分积分起止时间为(0，t)，第二部分积分起止时间为(t，Δt)，当Δt很小时，近似认为t和Δt时刻的应变率相等，则式(24)可化简为

(25)

至此，将超弹本构模型、黏弹本构模型的应力更新进行叠加，即获得了进行子程序开发所需的本构方程三维增量格式，子程序开发的任务就是在材料积分点上完成上式的应力计算，并对主程序进行应力更新。针对式(21)、式(25)和VUMAT所提供的数据接口，制定黏超弹本构模型子程序开发实施步骤为：

步骤1从ABAQUS主程序中读入增量步开始时刻材料属性：abA′a′b′θ1；变形梯度Ft、Ft+Δt；时间增量Δt等；

步骤2从用户自定义状态变量载入Green应变张量E,根据E=1/2(FTF-ξ)求解Green应变增量dE；

步骤3由式(21)计算Kirchhoff应力增量dS，根据σe=FSFT求解获得超弹本构模型σe的应力更新；

步骤4由式(25)计算获得粘弹本构模型σv应力更新

步骤5将超弹本构模型σe的应力更新和粘弹本构模型σv应力更新进行叠加，并返回增量步结束时刻的应力；

步骤6更新状态变量。

根据以上步骤，用FORTRAN语言编写子程序，从而将橡胶黏超弹本构模型嵌入到ABAQUS中。

3.3本构模型的一维有效性验证

为验证本构模型的一维有效性，将3.2节中开发的橡胶黏超弹本构模型的VUMAT子程序用于模拟单轴拉伸实验。见图3橡胶试件有限元模型所示，采用C3D8R单元进行网格划分，共计1866个单元，冲击加载以实验实测的入射杆应力波加载与入射杆端部，材料性能参数取表1中的数据。

图3　橡胶试件有限元模型 Fig.3 Finite element model of the rubber test specimen

通过数值模拟，获得了不同应变率下单轴拉伸实验的数值解。将实验数据与黏超弹本构的数值解进行对比验证。给出不同应变率下的工程应力P11-工程应变ξ11对比曲线。见图4，在工程应变ξ11<0.9范围内，工程应力数值解与单轴拉伸实验解符合较好，表明文中提出的黏超弹本构模型能够在较大范围内预测橡胶材料的单轴加载方向力学响应，验证了黏超弹本构模型的一维有效性。

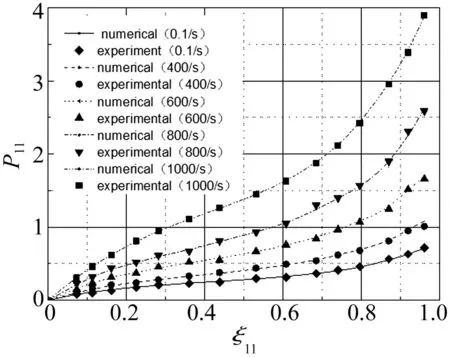
图4　不同应变率下应力-应变曲线对比 Fig.4 Stress-strain curves under different strain rate

3.4本构模型的三维有效性验证

为验证本构模型的三维有效性，将3.2节中开发的橡胶黏超弹本构模型的VUMAT子程序用于模拟文献[16]中橡胶衬套内表面扭转过程。见图6(a)橡胶衬套有限元模型所示，采用C3D8R单元进行网格划分，共计5760个单元，橡胶衬套内径9.85mm，外径18.2mm，轴向长度60mm。橡胶衬套外圈固定，分别以30°/s、15°/s、7.5°/s、3.75°/s、1.875°/s的加载率在内圈上施加15°的角位移，然后保持角位移不变。橡胶黏超弹本构模型的超弹性参数利用文献[16]中的单轴静态拉伸实验数据进行拟合，黏弹性参数和松弛时间则利用文献[16]中加载率为0.25mm/s的位移加载实验数据进行拟合，获得文献[16]中橡胶材料黏超弹本构模型的参数拟合值，见表2。

表2　文献[16]中黏超弹本构模型参数值

图6　橡胶衬套有限元模型和松弛状态应力云图 Fig.6 Finite element model bushing and stress nephogram in relaxed state of the rubber

图7　橡胶衬套内表面扭矩时程曲线数值解与实验解 [16] Fig.7 Numerical and experimental [16] results of the moment history curve for the inner surface of the rubber bushing

通过数值计算，获得橡胶衬套松弛状态下的应力云图和内表面的扭矩时程响应。不同角位移加载率下橡胶衬套松弛状态下的应力云图均见图6(b)，这是由于橡胶材料的记忆衰退特性，在角位移加载保持恒定一段时间后，不同加载率下的橡胶衬套进入同一稳定状态；见图7，将橡胶衬套内表面受到的扭矩时程响应数值解和文献[16]中实验值进行对比，扭矩时程响应数值解和实验解符合较好，验证了橡胶黏超弹本构模型的三维有效性。

4本构模型的应用

为表明黏超弹本构模型描述高应变率效应的实用性，建立两种选用不同本构模型(M-R超弹性本构、黏超弹性本构)的橡胶底座冲击附加载荷计算模型，并将冲击附加载荷实验值与数值仿真进行对比验证。

4.1冲击附加载荷计算数值模型

橡胶底座常用于文献[1]中所述的导弹悬垂弹射系统。见图8中橡胶底座冲击附加载荷计算数值模型所示，弹射冲击瞬间，高压气体充入橡胶底座内部，底座发生膨胀变形，最后与地面接触，释放压力达到平衡状态，作用在底座上的气体压力不能全部传递到地面，底座对初容室底部形成“附加载荷”。

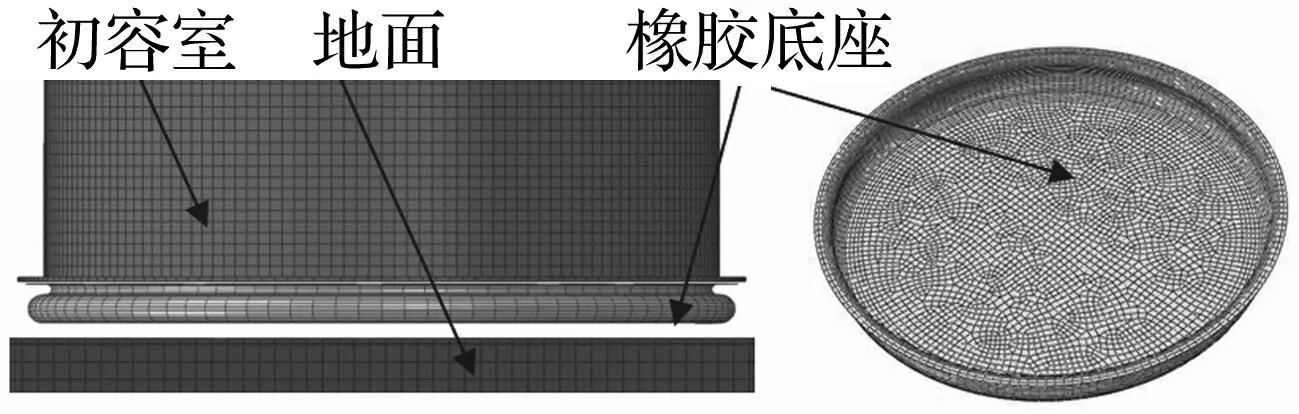
图8　冲击附加载荷计算数值模型 Fig.8 Numerical calculation model for the impact additional load

橡胶底座由橡胶层和帘子布多层粘接热压而成，采用S4R单元对底座结构进行离散。采用Rebar单元模拟帘子布增强相；为对比应变率效应，分别采用M-R超弹性本构模型和本文提出的黏超弹本构模型用户子程序来模拟橡胶材料；初容室和地面分别赋予相应的材料属性。在数值模型中定义橡胶底座上端面和初容室底部固连，底座底面与地面之间建立接触关系，在初容室与底座的连接界面上提取冲击附加载荷作用力。

4.2附加载荷实验与分析

见图9，附加载荷测量实验平台由底座、初容室、测力传感器、支撑台架等部件构成。通过进气阀在底座内部进行加压，底座膨胀与地面接触后对初容室产生附加载荷。冲击附加载荷通过初容室上端面传递至支撑台架，利用周向均布的三个测力传感器测量初容室上端面与支撑台架之间的作用力，冲击附加载荷值远大于初容室的自身重力，该作用力可视为冲击附加载荷。

图9　实验平台示意图 Fig.9 Schematic diagram of experimental platform

针对实验模型，将三个测点的作用力曲线叠加得到冲击附加载荷曲线，在橡胶材料参数不同的两类中数值模型中分别提取附加载荷。对计算结果进行无量纲化处理，将附加载荷除以底座内部压强峰值p与底座上端面的面积S的乘积，图10给出了冲击附加载荷随无量纲化时间变化曲线。

图10　冲击附加载荷对比 Fig.10 Comparison of additional impact load

由图7可知，两类橡胶材料参数不同的数值模型附加载荷数值解与实验值变化规律一致，但M-R超弹性本构模型的计算结果与实验存在明显的相位差，而文中提出的黏超弹本构模型计算结果与实验符合较好，附加载荷峰值的相对误差约为7%，满足工程精度要求，表明了黏超弹本构模型描述高应变率效应的实用性。

5结论

本文结合Exp-ln超弹性本构模型、广义黏弹性方法，建立了橡胶材料黏超弹本构模型；通过用户子程序验证了其有效性；将黏超弹本构模型应用于橡胶底座的建模。得到了一些结论：

(1) 随应变率的增大，橡胶材料单轴拉伸的应力增大，橡胶材料表现出应变率硬化效应。橡胶材料的力学响应与应变率密切相关。

(2) 黏超弹本构模型的超弹性部分采用参数少且物理意义明确的Exp-ln本构模型，黏弹性部分则建立在应变、时间效应解耦的基础上。本文提出的黏超弹本构模型预测应变范围大、参数少且物理意义明确。

(3) 在工程应变ξ11<0.9范围内，工程应力数值解与单轴拉伸实验解符合较好；橡胶衬套松弛状态下的应力云图和内表面的扭矩时程响应与文献中实验符合较好，验证了文中提出的黏超弹本构模型及其用户子程序的一维和三维有效性。

(4)相较于传统的超弹性本构模型，采用黏超弹性本构模型的底座数值模型仿真结果与冲击附加载荷的实验曲线符合较好，峰值误差约为7%，表明了文中黏超弹本构模型及用户子程序描述高应变率效应的实用性。

文中研究方法和结论能够为橡胶材料的力学响应预测提供技术支撑。

参考文献

[1]仲健林,任杰,马大为,等. 基于细观力学精确建模方法的自适应底座力学性能研究[J]. 固体火箭技术,2014,3:400-407.

ZHONG Jian-lin,REN Jie,MA Da-wei,et al. Mechanical properties research on adaptive base based on micromechanics accurate modeling method[J]. Journal of Solid Rocket Technology,2014,3: 400-407.

[2]Drozdov A D, deC Christiansen J. Consti-tutive equations in finite elasticity of swollen elastomers [J]. International Journal of Solids and Structures, 2013, 50(9):1494-1504.

[3]Kovalev V A, Radaev Y N. Three-dimensional constitutive relations of ideal plasticity and the flow on the coulomb-trescaprism edge[J]. Mechanics of Solids, 2010, 45 (2):295-308.

[4]Yang L M, Shim V P W, Lim C T. A visco-hyperelastic approach to modeling the constitutive behavior of rubber[J]. International Journal of Impact Engineering, 2000, 24(6): 545-560.

[5]Yang L M, Shim V P W. A visco-hyperelastic constitutive description of elastomeric foam[J]. International Journal of Impact Engineering, 2004, 30(8):1099-1110.

[6]周相荣,王强,王宝珍,等.一种基于Yeoh函数的非线性黏超弹本构模型及其在冲击仿真中的应用[J].振动与冲击,2007,26(5):33-37.

ZHOU Xinag-rong, WANG Qiang, WANG Bao-zhen, et al. A nonlinear visco-hyperelastic constitutive model based on Yeoh strain energy function with its application to impact simulation[J]. Journal of Vibration and Shock, 2007,26(5):33-37.

[7]Pouriayevali H, Guo Y B, Shim V P W. A viscohyperelastic constitutive description of elastomer behavior at high strain rates [J]. Procedia Engineering, 2011, 10: 2280-2285.

[8]常新龙,赖建伟,张晓军,等.HTPB推进剂高应变率黏弹性本构模型研究[J].推进技术, 2014, 35(1):123-127.

CHANG Xin-long, LAI Jian-wei, ZHANG Xiao-jun, et al.High strain rate visco-elastic constitutive model for HTPB propellant[J]. Journal of Propulsion Technology, 2014,35(1):123-127.

[9]Chen X H. Nonlinear electro-thermo-visco-elasticity [J]. Acta Mechanica,2010,211 (1/2): 49-59.

[10]胡少青，鞠玉涛，常武军，等. NEPE固体推进剂粘一超弹性本构模型研究[J].兵工学报,2013,34(2):168-173.

HU Shao-qin, JU Yu-tao,CHANG Wu-jun, et al. A visco-hyperelastic constitutive behaviour of NEPE propellant[J]. Acta ArmamentarII, 2013,34 (2):168-173.

[11]Khajehsaeid H, Arghavani J, Naghdabadi R. A hyperelastic constitutive model for rubber-like materials[J]. European Journal of Mech-anics/A Solids, 2013,38: 144-151.

[12]Gamonpilas C,McCuiston R. A nonlinear viscoelastic material constitutive model for polyurea[J]. Polymer,2012,53(17):3655-3658.

[13]Li Shao-hua, Yang shao-pu,Chen Li-qun, et al.A nonlinear vehicle-road coupled model for dynamics research[J].Journal of Computational and Nonlinear Dynamics,2013, 8(2): 1-14.

[14]Anani Y, Alizadeh Y. Visco-hyperelastic consti-tutive law for modeling of foam’s behavior[J]. Materials and Design, 2011,32:2940-2948.

[15]张伟, 魏刚, 肖新科,等.2A12铝合金本构关系和失效模型[J].兵工学报,2013,34(3):276-282.

ZHANG Wei, WEI Gang, XIAO Xin-ke, et al. Constitutive relation and fracture criterion of 2A12 aluminum alloy[J]. Acta ArmamentarII, 2013,34(3):276-282.

[16]Kadlowec J, Wineman A, Hulbert G. Elastomer bushing response: experiments and finite element modeling[J]. Acta Mechanica, 2003, 163(1/2): 25-38.