基于MIMO信号降噪的模态参数识别研究

基于MIMO信号降噪的模态参数识别研究

包兴先1，熊丛博2，李翠琳3，田玉芹4

(1.中国石油大学(华东) 石油工程学院，山东青岛266580； 2.国家海洋局第一海洋研究所，山东青岛266061；3.中国科学院海洋研究所中国科学院海洋地质与环境重点实验室，山东青岛266071； 4.青岛黄海学院交通与船舶工程学院,山东青岛266427)

摘要：发展了一种基于多输入多输出(MIMO)信号降噪的模态参数识别方法。首先对实测的MIMO脉冲响应数据构建block-Hankel矩阵，然后通过模型阶次指标确定矩阵的秩，进而基于结构矩阵低秩逼近(SLRA)计算得到降噪后的信号，最后通过多参考点复指数法(PRCE)识别结构的模态参数。数值算例和模型实验结果表明，该方法对实测MIMO信号有很好的降噪作用，识别效果较好。

关键词：多输入多输出；模型阶次；低秩逼近；block-Hankel矩阵；模态参数识别

中图分类号:TU317

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.025

Abstract:A modal identification scheme based on denoising MIMO signals was proposed here. With this scheme, the measured MIMO impulse response data were firstly used to construct a block-Hankel matrix, and the rank of the matrix was determined based on the model order indicator, then the structured low rank approximation (SLRA) method was implemented to achieve the denoised data. Finally, the modal parameters were estimated by using the PRCE method from the denoised MIMO signals. The effectiveness of the proposed scheme was verified with numerical examples and model test results.

基金项目：国家自然基金项目(41272321);乌鲁木齐市应用开发研究计划(Y131320008) 国家高技术研究发展计划(2008AA05A302)

收稿日期：2014-12-03修改稿收到日期：2015-04-17 2015-02-15修改稿收到日期：2015-04-23

Modal parameters identification based on denoising MIMO signals

BAOXing-xian1,XIONGCong-bo2,LICui-lin3,TIANYu-qin4(1. School of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China；2. The First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China；3. CAS Key Laboratory of Marine Geology and Environment, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China；4. School of Commumications and Ship Engineering, Qingdao Huanghai University, Qingdao 266427, China)

Key words:MIMO; model order; low rank approximation; block-Hankel matrix; modal parameters identification

对于大型复杂结构的模态测试，如桥梁、海洋平台等，单点激励往往能量不够，且在传递过程中损耗很大，离激励点较远的地方，响应信号较弱，信噪比较小。若加大激励力，则容易产生局部响应过大，造成非线性现象。若激励点正好处于某阶模态的节点位置，对该阶模态来说，系统将成为不可控和不可观的，就会发生漏失模态的现象。20世纪80年代起，陆续出现了一些多输入多输出(MIMO)的模态参数辨识方法，以弥补单点激励的缺点，如多参考点复指数法(PRCE)、特征系统实现算法(ERA)等[1]。然而，由于实测信号不可避免地受到测试环境、电子设备等背景噪声的干扰，因此识别结果通常包含虚假模态[2-3]。

为了区分真实模态和虚假模态,目前大多采用稳定图方法。由于计算采用的模型阶次高于真实的模型阶次，从而容许了噪声模态的存在[1]。而通过稳定图法并不能完全排除噪声模态，特别是随着模型阶次的升高，一些虚假模态往往容易趋于稳定，用稳定图很难正确识别出结构的真实模态参数[4-5]。而且稳定图法在很大程度上依赖于使用者的经验判断，当信号的信噪比低的时候，如何区分大量的虚假模态和真实模态将变得很困难。近年来，有学者发展了基于信号降噪的模态参数识别方法，即对响应信号先进行降噪处理，然后再进行模态参数识别，该方法能够提高模态参数的识别效率和精度。信号降噪的方法一般分为两类：一类是小波去噪方法，如陆秋海等[6]采用小波去噪方法来提高ERA/DC的识别精度，汤宝平等[7]基于小波去噪和HHT进行模态参数识别，以改善模态参数识别的精度等。但小波函数及其阈值的选取对模态参数识别的效果影响较大。另一类是奇异值分解(SVD)的方法，如练继建等[8]对时域振动响应信号采用奇异熵定阶降噪的方法对水工结构进行模态识别，Sanliturk等[9]对频响函数首先进行SVD降噪，然后再进行模态识别等。而通常采用的SVD降噪的方法，只对原始信号进行一次“分解-重构”，导致降噪效果没有达到最优。近年来，线性数学中的结构矩阵低秩逼近(Structured Low Rank Approximation，SLRA)方法被引入到模态参数识别中[3,10-11]。该方法基于SVD对脉冲响应函数进行迭代降噪，可以优化降噪效果，目前主要针对单点响应信号，若应用于多点响应信号，就需要对每一信号分别进行降噪，这显然会降低计算效率。

本文将单点响应信号的SLRA降噪方法扩展到MIMO信号统一降噪，然后进行模态参数识别。与传统的MIMO模态参数识别方法直接采用实测信号进行模态分析不同，该方法首先采用实测的MIMO脉冲响应信号构建block-Hankel矩阵，然后进行模型定阶及SLRA计算，以获得降噪信号，最后利用PRCE法对降噪信号进行模态参数识别。文中将通过质量-弹簧-阻尼系统的数值算例和导管架式海洋平台的物理模型实验验证该方法的有效性。

1基于MIMO信号降噪的模态参数识别

1.1构建block-Hankel矩阵

一个N自由度的动力系统在p点施加脉冲激励得到q点的脉冲响应函数可以表示为：

(1)

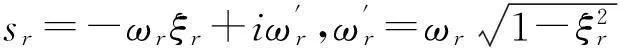
当实测结构的脉冲响应函数hpq(t)中包含未知的M阶模态，并以采样间隔Δt表示成离散形式时，则tk=kΔt时刻的脉冲响应函数矩阵可表示为：

hk=WZkΦT

(2)

式中，hk∈RNin×Nout，W∈RNin×2M ，Φ∈RNout×2M ，Z=diag{es1Δt ,…,es2MΔt }为对角矩阵，k=0,1,2,…。R代表实数矩阵，其上标代表矩阵维数。

基于hk构建mNin×nNout维的block-Hankel矩阵HmNin×nNout。其中，矩阵HmNin×nNout中每一个独立的块(block，即hk)都是由tk时刻对应Nin个激励点Nout个响应点的脉冲响应信号构建成的Nin×Nout维的矩阵，mNin,nNout≥2M，x=m+n-2。

(3)

1.2模型定阶

应用SVD确定矩阵HmNin×nNout的秩，即

HmNin×nNout=UΣVT

(4)

式中，U∈RmNin×mNin，VT∈RnNout×nNout是正交矩阵，其上标T代表矩阵的转置，Σ∈RmNin×nNout是对角矩阵，其对角元素为降序排列的奇异值。而Σ可分解为g个非零奇异值子矩阵Σg和几个零子矩阵：

(5)

这一分解表明矩阵HmNin×nNout的秩是g。

1.3SLRA

理论上，对于本文脉冲响应信号的降噪技术，属于线性数学中的SLRA范畴，即通过获得Frobenius范数意义下的最佳逼近结构矩阵来降低噪声[13]。

当hpq受到随机噪声的干扰时，可以写成：

(6)

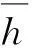
(7)

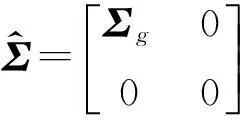
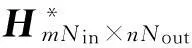
步骤(1)和(2)交替迭代，直到满足收敛标准。

1.4模态参数识别

基于上述步骤确定的模型阶次以及降噪后的MIMO脉冲响应信号，采用PRCE法进行模态参数识别。PRCE法是近年来广泛应用的MIMO模态参数识别方法，该方法的理论推导过程在此不再赘述，读者可参阅相关文献[1]等。综上，基于MIMO信号降噪的模态参数识别方法的流程图如下：

图1　基于MIMO信号降噪的模态参数识别方法流程图 Fig.1 The flow chart of MIMO modal parameters identification method based on noise rejection

2数值算例

2.1数据的模拟

建立一个五自由度的质量-弹簧-阻尼系统的数值模型见图2。单元的质量、刚度和阻尼系数分别为mn=50 kg、kn=2.9×107N/m、cn=1000 N·s/m。通过特征值分析，得到模态频率的理论值为：34.499 Hz、100.70 Hz、158.730 Hz、203.880 Hz、232.520 Hz；模态阻尼比的理论值为：0.0037374、0.010909、0.017197、0.022092、0.025198。

图2五自由度质量-弹簧-阻尼系统
Fig.2 A 5-DOF mass-spring-dashpot system

采用Matlab编制程序，分别在m1、m2两处施加脉冲激励，采样频率500 Hz，各得到m1、m2、m3、m4、m5五处脉冲响应信号，共10个。每个响应信号包含1024个采样点，取前500个采样点进行后续分析。脉冲响应函数经傅里叶变换可得到频率响应函数。

通过对10个精确的(不含噪声的)响应信号统一叠加10%的高斯白噪声来模拟含噪声的响应信号。噪声水平10%，代表白噪声的标准差和精确信号的标准差之比为10%。以m1处激励，m1处响应的信号为例，精确信号和含噪信号的频率响应函数图见图3。

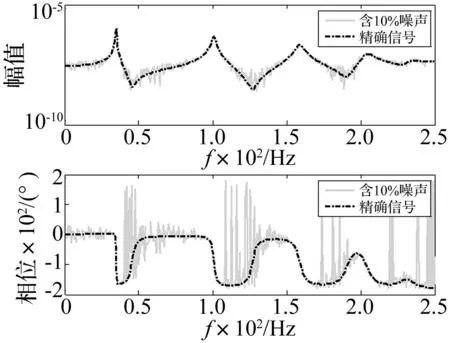
图3　m 1处激励，m 1处响应的精确信号和 含10%噪声信号对比 Fig.3 The comparison of noise free signal and signal with 10% noise with respect to input m 1 and output m 1

2.2模型定阶和信号降噪

分别对精确信号和含噪信号构建block-Hankel矩阵H40×2405(即HmNin×nNout，m=20，n=481，Nin=2，Nout=5),对其进行SVD计算，得模型阶次指标MOI，见图4。可以看出，受噪声的影响，MOI最大值由精确信号的7500，减小到含噪信号的2.7，而对应的模型阶次都为10，说明信号中都包含5阶模态。模型定阶后，对含噪信号构建的block-Hankel矩阵进行SLRA降噪计算。

图4　精确信号和含10%噪声信号的模型阶次指标 Fig.4 Model order indicators of noise free signal and signal with 10% noise

2.3模态参数识别

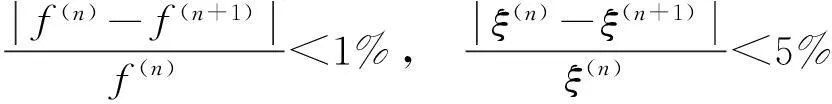
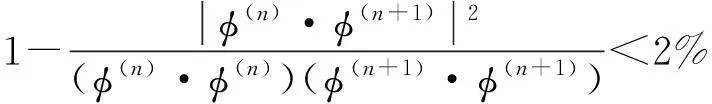
式中，f(n)，ξ(n)和φ(n)分别代表阶次为n时识别的频率、阻尼比和模态向量。当由相邻阶次识别的频率、阻尼比和模态向量同时满足上式时，可认为识别结果为稳定的，否则为不稳定。

从图5可以看出，由于噪声的干扰，传统的PRCE方法未能识别出稳定的第一阶模态。而且随着阶次的增大，在170Hz和240Hz附近有趋于稳定的虚假模态出现。从图6可以看出，采用本文方法能够很好地识别出稳定的5阶模态。基于含噪及降噪信号的识别结果见表1和表2。通过与理论值对比发现，由降噪信号识别的频率和阻尼比的误差范围分别为0～0.90%和0.06%～5.73%，均小于由含10%噪声识别的频率和阻尼比的误差。

图5　传统的PRCE方法识别结果的稳定图 (*：稳定，°：不稳定) Fig.5 Stability diagram obtained from implementing the traditional PRCE method (*: stable, °: unstable)

模态理论含噪误差/%降噪误差/%134.499--34.5400.902100.70100.790.09100.7003158.73158.870.09158.750.014203.88203.960.04203.920.025232.52232.690.07232.560.02

表2　采用含10%噪声信号和降噪信号识别的阻尼比(%)

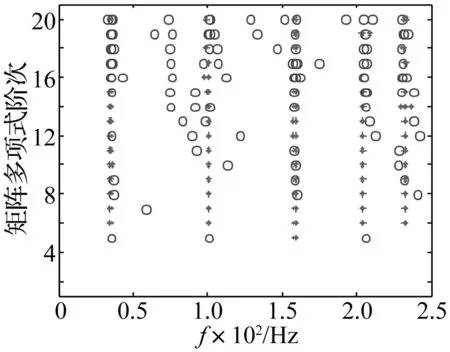
图6　基于MIMO信号降噪的PRCE方法识别 结果的稳定图(*：稳定，°：不稳定) Fig.6 Stability diagram obtained from implementing the proposed method (*: stable, °: unstable)

2.4不同激励组合下的模态参数识别

在不同激励组合情况下验证本文方法的有效性。组合1：如前所述，m1、m22处激励，各5处响应；组合2：m3、m42处激励，各5处响应；组合3：m1、m2、m33处激励，各5处响应；组合4：m1、m2、m3、m44处激励，各5处响应。组合2、3、4的分析步骤同组合1。各组合的含噪信号经模型定阶确定阶次均为10。对含噪信号构建的block-Hankel矩阵进行SLRA降噪计算。采用传统的PRCE法(基于含噪信号)及基于MIMO信号降噪的PRCE法分别进行模态参数识别，组合2的识别结果的稳定图见图7和图8，组合3的识别结果的稳定图见图9和图10，组合4的识别结果的稳定图见图11和图12。

从图7、图9、图11可以看出，由于噪声的干扰，各组合情况下，传统的PRCE方法均未能识别出稳定的第一阶模态。而且随着阶次的增大，在170Hz和240Hz附近均有趋于稳定的虚假模态出现。从图8、图10、图12可以看出，采用本文方法能够很好地识别出稳定的5阶模态。篇幅所限，识别的频率和阻尼比值从略。同样，从组合1、2、3、4的传统方法的识别结果(图5、7、9、11)可以发现，要获得稳定的识别结果(第一阶除外)，需要的最小矩阵多项式阶次分别为：10、9、6、4，而采用本文方法各组合(图6、8、10、12)要获得稳定的5阶识别结果，需要的最小矩阵多项式阶次分别为：6、6、5、3。这表明，随着组合中响应数据增多，要获得稳定的识别结果，需要的最小矩阵多项式阶次也减少。对同一组合，要获得稳定的识别结果，本文方法所需的最小矩阵多项式阶次小于传统方法。

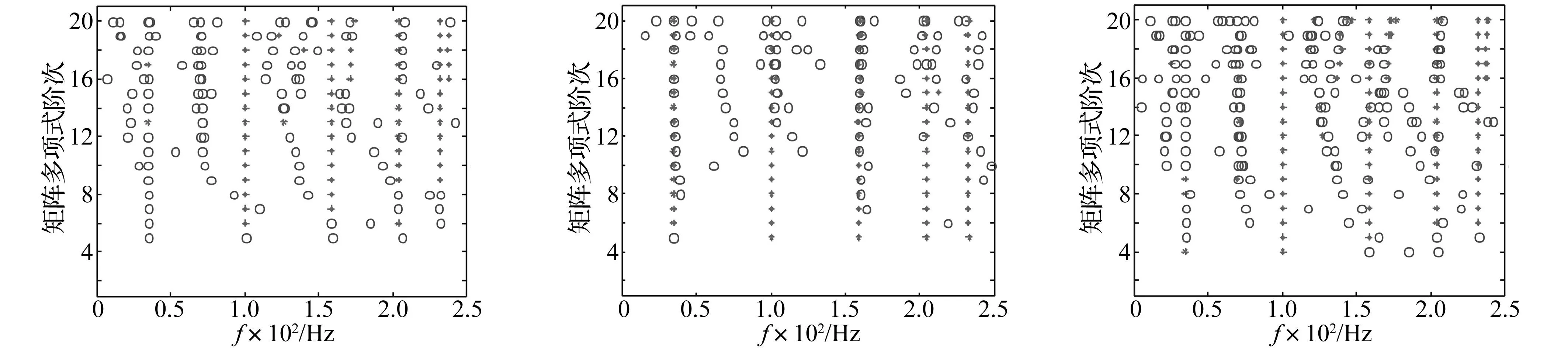
图7 组合2:传统的PRCE方法识别结果的稳定图(*:稳定,°:不稳定)Fig.7Case2:stabilitydiagramobtainedfromimplementingthetraditionalPRCEmethod(*:stable,°:unstable)图8 组合2:基于MIMO信号降噪的PRCE方法识别结果的稳定图(*:稳定,°:不稳定)Fig.8Case2:stabilitydiagramobtainedfromimplementingtheproposedmethod(*:stable,°:unstable)图9 组合3:传统的PRCE方法识别结果的稳定图(*:稳定,°:不稳定)Fig.9Case3:stabilitydiagramobtainedfromimplementingthetraditionalPRCEmethod(*:stable,°:unstable)

图10 组合3:基于MIMO信号降噪的PRCE方法识别结果的稳定图(*:稳定,°:不稳定)Fig.10Case3:stabilitydiagramobtainedfromimplementingtheproposedmethod(*:stable,°:unstable)图11 组合4:传统的PRCE方法识别结果的稳定图(*:稳定,°:不稳定)Fig.11Case4:stabilitydiagramobtainedfromimplementingthetraditionalPRCEmethod(*:stable,°:unstable)图12 组合4:基于MIMO信号降噪的PRCE方法识别结果的稳定图(*:稳定,°:不稳定)Fig.12Case4:stabilitydiagramobtainedfromimplementingtheproposedmethod(*:stable,°:unstable)

3模型实验

一钢质导管架式海洋平台物理模型见图13，主腿尺寸为Φ25mm×2.5mm，横撑及斜撑尺寸均为Φ15mm×1.5mm。将模型底部固定，在各层关键节点(如点1、2)布置各向加速度传感器，采用力锤在甲板角(点3、4)处分别施加X向和Y向的脉冲激励，采样频率200 Hz，得到两节点(点1、2)处的X、Y向响应信号，约45s。后续分析取各信号的一段，512个数据点。基于m=20，n=493，Nin=2，Nout=4构建block-Hankel矩阵H40×1972。由模型阶次指标MOI(见图14)确定模型阶次为6，说明信号中包含3阶模态。由于激励位置位于甲板角，因此模型的X、Y向平动模态和扭转模态都可能被激励出来。确定模型阶次后，对由实测信号构建的block-Hankel矩阵H40×1972进行SLRA降噪计算。

图13　导管架式海洋平台模型 Fig.13 Jacket offshore platform model

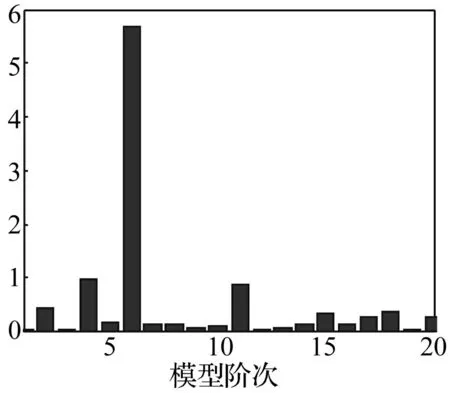
图14　实测信号的模型阶次指标 Fig.14 Model order indicators of measured signal

采用传统的PRCE法(基于实测信号)及基于MIMO信号降噪的PRCE法分别进行模态参数识别，识别结果的稳定图见图15和图16。可以看出，基于实测信号只能识别出稳定的第一阶模态。第二、三阶模态因为受噪声影响未识别出稳定的结果。采用本文方法能够很好地识别出信号中包含的3阶模态。基于实测及降噪信号的识别结果见表3。尽管无法得到物理模型的真实模态参数，但是可以通过比较两种方法识别结果的稳定图，以及有限元模型的频率参考值来评价识别效果。结果表明，与传统的PRCE法相比，本文方法识别效果较好。

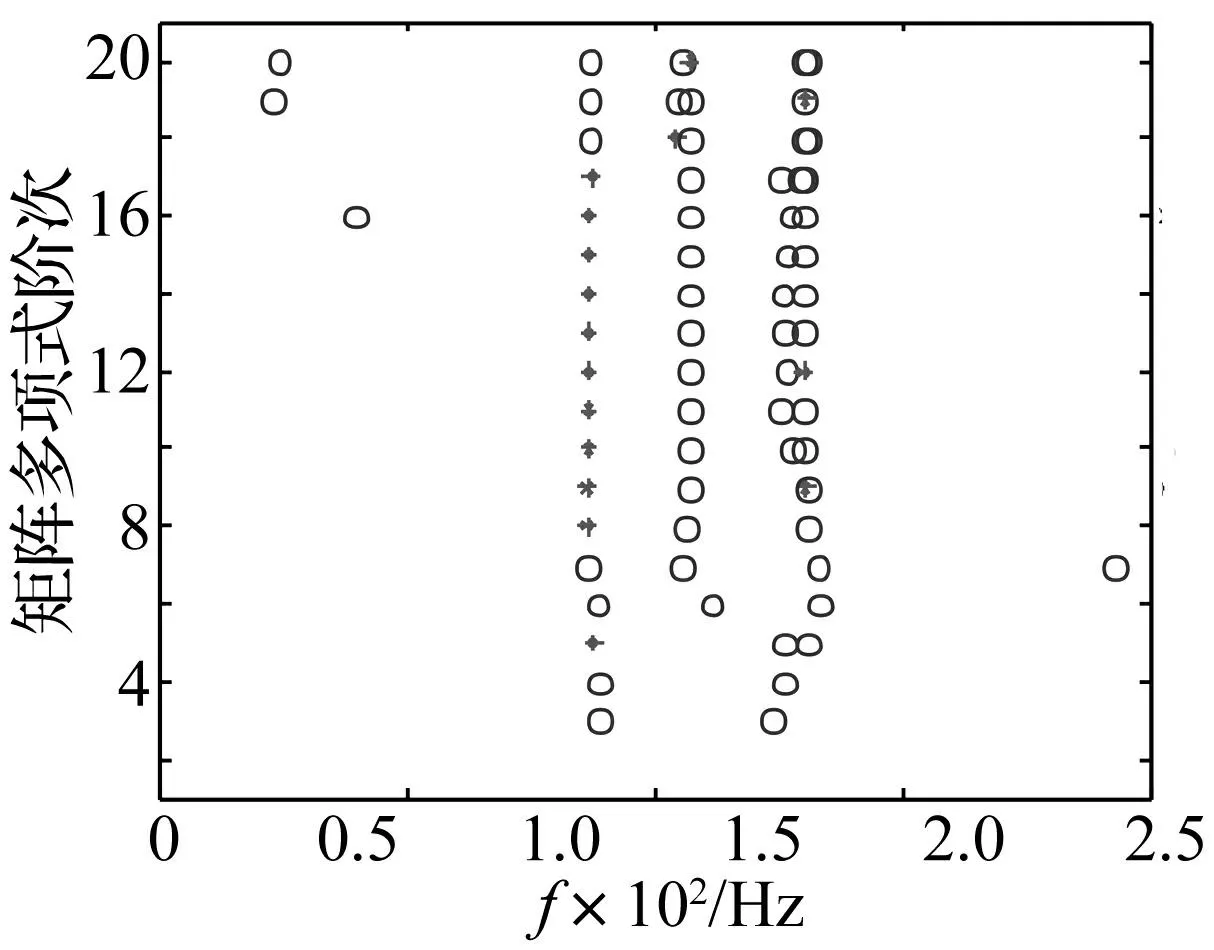
图15　传统的PRCE方法识别结果的稳定图 (※：稳定，○：不稳定) Fig.15 Stability diagram obtained from implementing the traditional PRCE method (※: stable, ○: unstable)

图16　基于MIMO信号降噪的PRCE方法识别结果的 稳定图(※：稳定，○：不稳定) Fig.16 Stability diagram obtained from implementing the proposed method (※: stable, ○: unstable)

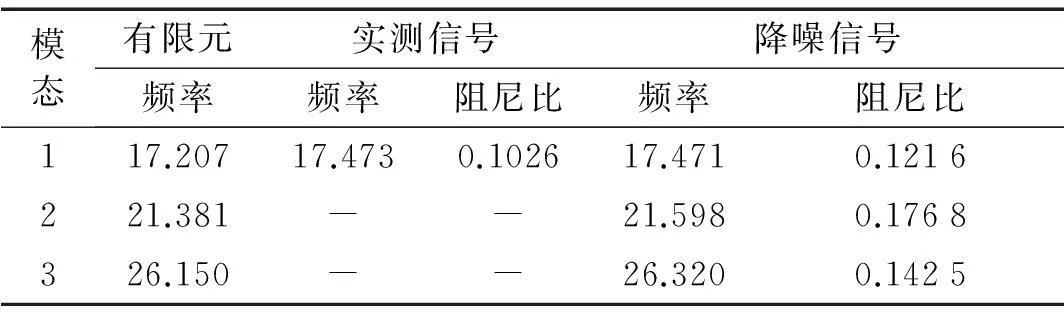
模态有限元实测信号降噪信号频率频率阻尼比频率阻尼比117.20717.4730.102617.4710.1216221.381--21.5980.1768326.150--26.3200.1425

4结论

(1)本文发展了一种基于MIMO测试信号统一降噪的模态参数识别方法。该方法首先对测试的MIMO响应数据构建block-Hankel矩阵，通过模型阶次指标确定矩阵的秩，进而基于SLRA方法得到降噪后的信号，最后通过PRCE方法识别结构的模态参数。

(2)5自由度质量-弹簧-阻尼系统数值算例的结果表明，与传统的直接采用实测信号进行MIMO模态参数识别的方法相比，本文方法的识别精度较高，而且能识别出传统方法遗漏的第一阶模态。此外，随着模态识别中采用的响应数据增多，要获得稳定的识别结果，需要的最小矩阵多项式阶次也减少。对相同的响应数据组合，要获得稳定的识别结果，本文方法所需的最小矩阵多项式阶次也小于传统方法。

(3)通过导管架式海洋平台物理模型实验进一步验证本文方法的有效性。结果表明，与传统方法相比，本文方法的识别效果较好，能够识别出传统方法因噪声影响而遗漏的模态。

参考文献

[1]Ewins D J. Modal Testing: Theory, Practice and applications [M]. 2nd ed, Baldock, Hertfordshire, England: Research Studies Press, 2000.

[2]Wang Shu-qing, Liu Fu-shun. New accuracy indicator to quanfity the true and false modes for eigensystem realization algorithm [J]. Structural Engineering and Mechanics, 2010, 34(5): 625-634.

[3]Hu S L J, Bao X X, Li H J. Model order determination and noise removal for modal parameter estimation[J]. Mechanical Systems and Signal Processing, 2010, 24(6): 1605-1620.

[4]易伟建，刘翔.动力系统模型阶次的确定[J].振动与冲击, 2008, 27(11): 12-16.

YI Wei-jian, LIU Xiang. Order identification of dynamic system model[J]. Journal of Vibration and Shock, 2008,27(11): 12-16.

[5]常军，张启伟，孙利民.稳定图方法在随机子空间识别模态参数中的应用[J].工程力学, 2007, 24(2): 39-44.

CHANG Jun, ZHANG Qi-wei, SUN Li-min. Application of stabilization diagram for modal paramenter identification using stochastic subspace method[J].Engineering Mechanics, 2007, 24(2): 39-44.

[6]林贵斌，陆秋海，郭铁能. 特征系统实现算法的小波去噪方法研究[J]. 工程力学, 2004, 21(6): 91-96.

LIN Gui-bin, LU Qiu-hai, GUO Tie-neng. A study of denoising method for Eigensystem Realization Algorithm based on wavelet analysis[J]. Engineering Mechanics, 2004,21(6): 91-96.

[7]汤宝平，何启源，蒋恒恒，等. 利用小波去噪和HHT的模态参数识别[J]. 振动、测试与诊断, 2009, 29(2): 197-200.

TANG Bao-ping, HE Qi-yuan, JIANG Heng-heng, et al. Modal parameter identification based on Hilbert Huang Transform and wavelet denoising[J]. Journal of Vibration, Measurement & Diagnosis, 2009, 29(2): 197-200.

[8]练继建，李火坤，张建伟. 基于奇异熵定阶降噪的水工结构振动模态ERA识别方法[J]. 中国科学E辑:技术科学, 2008, 38(9): 1398-1413.

LIAN Ji-jian, LI Huo-kun, ZHANG Jian-wei. The ERA modal parameters identification for hydro-structures based on model order determination and noise reduction using singular entropy[J]. Science in China :Series E: Technological Sciences, 2008, 38(9): 1398-1413.

[9]Sanliturk K Y, Cakar O, Noise elimination from measured frequency response functions[J]. Mechanical Systems and Signal Processing, 2005, 19: 615-631.

[10]包兴先，李昌良，刘志慧.基于低秩Hankel矩阵逼近的模态参数识别方法[J].振动与冲击, 2014, 33(20): 57-62.

BAO Xing-xian, LI Chang-liang, LIU Zhi-hui. Modal parameters identification based on low rank approximation of a Hankel Matrix[J]. Journal of Vibration and Shock, 2014,33(20): 57-62.

[11]包兴先，刘福顺，李华军，等. 复指数方法降噪技术及其试验研究[J]. 中国海洋大学学报, 2011, 41(1/2): 155-160.

BAO Xing-xian, LIU Fu-shun, LI Hua-jun, et al. The complex exponential method based on singal-noise separation for modal analysis[J]. Periodical of Ocean University of China, 2011, 41(1/2): 155-160.

[12]王树青，林裕裕，孟元栋，等.一种基于奇异值分解技术的模型定阶方法[J].振动与冲击, 2012, 31(15): 87-91.

WANG Shu-qing, LIN Yu-yu, MENG Yuang-dong, et al. Model order determination based on singular value decomposition[J].Journal of Vibration and Shock, 2012, 31(15): 87-91.

[13]De Moor B. Total least squares for affinely structured matrices and the noisy realization problem[J]. IEEE Trans Signal Process, 1994, 42(11):3104-3113.

第一作者邹新宽男，博士生，1985年生

通信作者张继春男，博士,教授,博士生导师，1963年生

第一作者徐宁男，博士，工程师，1983年生

通信作者刘占生男，教授,博士生导师，1962年生