人字桥梁多维地震作用下振动台试验研究

人字桥梁多维地震作用下振动台试验研究

李青宁1，尹俊红1，闫磊1，程麦理1，廖鑫1，张瑞杰1，李桅2

(1.西安建筑科技大学土木工程学院，西安710055; 2.温州大学建筑工程学院，浙江温州325035)

摘要：按1/20的几何比例制作一典型人字曲线桥梁模型,进行了多维振动台试验，并针对试验模型建立数值分析模型，研究人字曲线桥梁在多维地震作用下的地震响应特点。结果表明，竖向地震分量对桥墩顶纵桥向加速度、主梁分支处两桥墩横桥向相对位移和墩底纵桥向弯矩基本无影响，结构响应与输入地震波的频谱特性和结构形式有关；单向激励下，墩顶纵桥向加速度、分支处桥墩横桥向相对位移和墩底纵桥向弯矩响应都为最大；双向和三向激励都使墩顶纵桥向加速度响应降低，且降低幅度随着墩与直梁正向角度的增加而增加；主梁与分支直梁应设置的初始间隙应大于主梁与分支曲梁。

关键词：人字曲线桥梁；振动台；多维输入；地震响应；数值分析

中图分类号:U442.55文献标志码：A

基金项目：国家自然科学

收稿日期：2014-04-17修改稿收到日期：2014-07-04

基金项目：国家自然科学基金(51175518);湖南省科技型中小企业技术创新基金立项项目(12C26214305029)

收稿日期：2014-04-18修改稿收到日期：2014-07-30

Shaking table tests for a Y-shape bridge under multi-dimensional earthquake excitation

LIQing-ning1,YINJun-hong1,YANLei1,CHENGMai-li1,LIAOXin1,ZHANGRui-jie1,LIWei2(1. College of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China；2. College of Civil Engineering and Architecture, Wenzhou University, Wenzhou 325035, China)

Abstract:A scale 1/20 model of a typical Y-shaped curve bridge was made and its multi-dimensional shaking table tests were conducted. Its numerical analysis model was established, the seismic response characteristics of the Y-shaped curve bridge under multi-dimensional seismic excitation were studied.The results showed that the vertical seismic input has no effects on the vertical seismic input has no effects on the longitudinal acceleration at the pier top, the transverse relative displacement between two piers at the branch of the main beam and the longitudinal bending moment at the pier bottom, the structural response is related to the input seismic spectrum and structure form; the three ones mentioned above reach the maximum under unidirectional excitations; the longitudinal acceleration at the pier top drops under bidirectional excitations and three-dimensional excitations, and the reduction level increases with increase in the angle between pier and straight beam; the initial gap between the main beam and the branch straight beam should be larger than that between the main beam and the branch curve beam.

Key words:Y-Shaped curve bridge; shaking table; multi-dimensional excitation; seismic response; numerical analysis

人字曲线桥梁主要表现为主线桥梁与匝道桥梁的联结结构，一般由直线梁与曲线梁组成，被广泛用于城市高架和立交中。地震是一种破坏极大的自然灾害，因此有必要研究人字曲线桥梁在地震作用下的抗震性能。对于人字桥梁这种异形桥梁结构形式，研究者主要进行了模型的静力试验和数值分析[1]，还鲜有进行人字桥梁振动台试验。

在以往的振动台试验研究中，主要进行了规则桥梁[2-6]和一般曲线桥梁[7-9]的单向激励振动台试验，由于实际地震是多维的，单向激励并不能完全反映结构的真实响应，但目前对于桥梁多维输入的研究主要集中在理论和数值分析上，桥梁结构的地震反应比较复杂，与输入的地震动场地特性、桥梁结构自身特性有较大关系，因此进行人字桥梁多维振动台试验是研究该类型桥梁性能最有效和直接的方法，对人字桥梁的抗震理论研究和评估很有价值。基于此，本文选取典型人字曲线桥梁作为研究对象，按几何缩尺1/20的比例进行多维激励下的振动台试验，探讨结构在不同地震动输入方向下的地震响应, 为人字桥梁结构多维地震输入的动力响应计算理论和数值模拟提供试验依据。

1试验简介

1.1模型设计

模型为人字曲线桥梁，几何缩尺比为1/20。结构模型见图1，结构形式为一个主梁和两个分支梁，其中1#主梁为异形梁截面，分支梁包括2#简支梁和3#曲线连续梁两种结构形式，制作模型1#梁和2#梁模型每跨1.8 m，3#曲梁单跨跨度1m，曲率半径为40 m，模型墩高1.5 m，截面及配筋布置见图2。

图1　桥梁结构模型 Fig.1 The bridge model

图2　构件截面/cm Fig.2 Member section/cm

模型材料采用微粒混凝土与普通钢筋，采用微粒混凝土MC25模拟实际桥梁的普通混凝土C50。微粒混凝土可达到相同混凝土的强度，弹性模量较普通混凝土小，适宜于比例尺寸结构的振动台试验[10]。配筋采用HRB335级带肋钢筋，梁纵筋直径Φ6 mm，墩纵筋直径为Φ8 mm，箍筋都采用直径Φ6 mm光圆钢筋，钢筋骨架见图3，空心部分填充轻质泡沫板。1#墩和5#墩设置固定支座，其余均为普通橡胶支座，支座尺寸9 cm×9 cm×1.5 cm，水平剪切刚度kx=ky=3.8×106N/m，竖向刚度kz=7.1×107N/m。

图3　钢筋骨架 Fig.3 Framework of steel reinforcement

根据动力相似理论[11]，模型结构动力相似常数见表1。通过施加配重块满足动力质量相似，因墩体部分难以可靠的施加和固定配重块，只在梁体表面施加，采用每个质量为5 kg长方体形金属块，均匀布置于梁体之上，其中1#梁施加1 275 kg，2#梁施加555 kg，3#梁施加650 kg。配重块四周由锚固于梁体的挡板起固定和阻挡作用，质量块之间空隙采用泡沫胶填充以防止相对错动，布置见图4。

表1　模型相似关系

1.2输入地震波

试验在西安建筑科技大学结构与抗震实验室进行，振动台台面尺寸4.1 m×4.1 m，三向六自由度激振方式。模型结构底部通过高强螺栓与振动台台面连接，模拟墩底固结的边界条件，模型台面布置见图5。

图4　模型配重布置 Fig.4 Model artificial mass arrangement

图5　模型在振动台布置 Fig.5 Model on shaking table

激励地震波选用EL-centro波(N-S向和E-W向)和兰州波(N-S向和E-W向)，地震波及频谱曲线见图6。研究八度设防烈度下的结构响应，八度设防实际对应峰值0.2 g，因模型加速度相似系数为2.5，则在输入时的峰值为2.5×0.2 g=0.5 g。

以直梁纵桥向为X输入方向，直梁横桥向为Y输入方向，竖向为Z输入方向。采取3种激励方式: 单向X激励，双向XY激励, 三向XYZ激励，都采用一致激励输入。EL-centro 波(N-S)和兰州波(N-S)作为X向和Z向的激励波，EL-centro波(E-W)和兰州波(E-W)作为Y向激励波，多维输入时，输入地震波峰值之比，水平X向：水平Y向：竖Z向取为1∶0.85∶0.65，工况和峰值见表2。

图6　试验用波 Fig.6 Earthquake wave for test

工况加速度峰值/gX向Y向Z向扫描白噪声---EL-centro波0.5——EL-centro波0.50.425—EL-centro波0.50.4250.325兰州波0.5——兰州波0.50.425—兰州波0.50.4250.325

1.3测点布置

在台面布置三个方向的加速度计和位移计测试台面输出，在各个墩顶布置纵桥向加速度计，各梁跨中布置竖向加速度计和纵桥向位移计，2#墩和4#墩顶布置横桥向位移计。

2试验及结果分析

2.1动力特性

模型加载之前，用持时90s的白噪声对结构模型进行X向、Y向和Z向扫描，得到三向的传递函数。根据所采集到的结构传递函数的共振峰可得到结构的自振频率和动力放大系数，阻尼比通过半功率(带宽)法得到，见表3。该模型结构基频为Z向最大，Y向和X向次之。

表3　动力特性

2.2墩顶动力响应

表4列出了在EL-centro波激励下，不同方向激励下1#-6#墩顶纵桥向加速度及其变化幅度。可知，直线梁桥各墩顶纵桥向加速度响应均比台面输入波峰值有所放大，3#墩顶放大效应最为明显，放大系数为3.27；曲线梁桥各墩顶响应在单向激励下比台面输入波峰值有所放大，在多向激励下除布置稍微不规则的4#墩外，其余墩顶响应比台面输入波峰值都有所降低。

对于三种激励方式，墩顶纵桥向加速度响应不受竖向分量的影响，1#墩、2#墩和3#墩顶纵桥向加速度响应基本没有变化，其余各墩响应都比单向激励有所降低，6#墩顶响应降低幅度最大，为83.1%，5#墩降低幅度次之，为46.7%；其中在增加Y向输入后，3#曲线连续梁的4#墩、5#墩和6#墩墩顶纵桥向加速度降幅较大，主要是由于多维输入使人字桥梁结构产生扭转耦联的空间振动，桥梁振动的方向性减弱；同时，入射波角度发生改变，激发的结构振型也发生改变，当入射波为X向时，桥梁结构主振型为纵向，增加Y向输入后，主振型变为扭转，振型贡献也有不同，最终导致响应的差异。分析表明，多维输入对直线梁桥墩墩顶纵桥向加速度响应基本无影响，双向和三向激励都使曲线梁桥墩墩顶纵桥向加速度响应较单向激励降低，且降低幅度随着墩与台面正向角度的增加而增加，对于曲线桥梁结构，多维地震输入激起的结构反应不能简单分解为单个方向分别激起的结构反应的叠加。

2#墩和4#墩为人字曲线桥梁分支处的直线梁桥墩和曲线梁桥墩，为1#主梁共用，多维输入对 2#墩顶纵桥向加速度响应无影响，但是使 4#墩顶响应降低了12.4%，是因2#墩在振动台台面规则布置，4#墩布置与台面X向角度为6°，且直线梁桥和曲线梁桥动力特性不同，也使2#墩和4#墩响应出现差异。

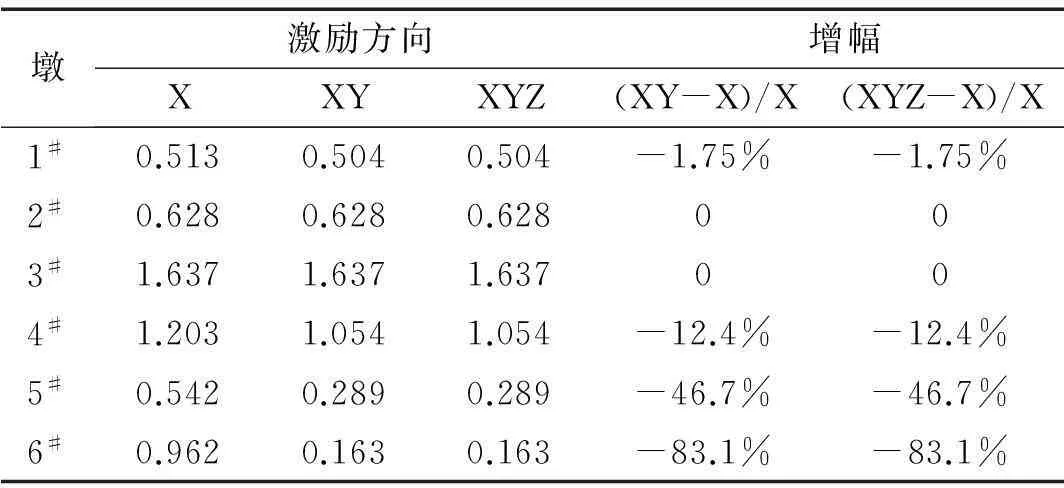
表4　墩顶纵桥向加速度响应(g)

2.3梁跨中动力响应

图7给出EL-centro波激励下，1#梁跨中、2#梁跨中、3#梁左跨跨中竖向加速度响应时程曲线，表5给出EL-centro波和兰州波激励下的竖向加速度响应峰值。可以看出，1#梁跨中、2#梁跨中、3#梁左跨跨中竖向加速度响应在三向和双向输入下都较单向输入有增加，增加幅值有所不同，1#梁跨中在三向和双向输入较单向输入增幅分别为971.2%和208.5%，2#梁跨中增幅分别为1 085%和142.4%，3#梁左跨中增幅分别为676.7%和104.2%，表明竖向地震动的输入对梁跨中竖向加速度响应的影响很大，对直线梁影响尤其显著；沿横桥向的地震输入对跨中响应也有影响，但没有竖向输入产生的影响强烈。

2#梁和3#梁为人字曲线桥梁分支直梁与曲梁，分支直梁跨径大于分支曲梁，在单向和双向激励下，分支曲梁跨中竖向加速度响应总是大于分支直梁，但在三向输入下，分支曲梁跨中竖向加速度响应小于分支直梁，1#主梁跨中响应介于2#梁和3#梁之间，说明人字桥梁分支曲梁跨中响应受水平输入的影响较分支直梁大，总体直线梁部分受竖向地震动分量的影响较为显著。

可以发现，人字桥梁每跨结构形式、质量、地震动特性的敏感带不同，对于输入相同的地震动则表现为不同的动力响应。竖向地震动的输入导致桥墩竖向拉伸及压缩应力的强烈振荡变化，从而使梁体跨中弯矩需求显著增加，可能会引起主梁受力超过其设计承载能力，甚至可能造成主梁钢筋屈服，这一现象与过去研究者的理论分析结果[12-13]相符。

表5　梁跨中竖向加速度响应峰值(g)

2.4邻梁纵向相对位移

为研究多维输入对纵向梁体碰撞的影响，将模型伸缩缝宽度设置为2cm，使结构不发生碰撞，通过研究梁体间的相对位移，分析多维输入使梁与梁发生碰撞的可能性及影响。

表6给出在EL-centro波和兰州波激励下，1#梁和2#梁、1#梁和3#梁之间的相对位移，若相对位移大于结构的伸缩缝宽度时，梁体之间必然发生碰撞。可以看出，在两种波的激励下，双向和三向输入都会使梁体之间的相对位移增大，表明双向输入和三向输入更容易使结构发生碰撞。在EL-centro波激励下，若使梁体间不发生碰撞，三向、双向和单向输入时1#伸缩缝宽度应不小于9.952 6 mm、10.770 8 mm和10.252 27 mm，伸缩缝最小宽度在三向和双向输入时较单向输入增幅为3.01%和8.22%；2#伸缩缝宽度应不小于1.2 mm、1.532 mm和2.433 mm，伸缩缝最小宽度在三向和双向输入时较单向输入增幅为102.75%和27.67%。在兰州波激励下，三向、双向和单向输入时1#伸缩缝宽度应不小于14.544 8 mm、19.347 mm和16.525 mm，伸缩缝宽度在三向和双向输入时较单向输入增幅为13.61%和33.02%；2#伸缩缝宽度最小应不小于1.552 8 mm、2.05 mm和1.67 mm，伸缩缝最小宽度在三向和双向输入时较单向输入增幅为7.55%和32.02%。

在EL-centro波和兰州波激励下，地震动各种输入下为使梁体之间不发生碰撞，1#伸缩缝应设置的最小宽度值大于2#伸缩缝，1#伸缩缝布置在直梁与直梁之间，2#伸缩缝布置在直梁与曲线梁之间，表明碰撞的发生不但与地震的输入有关，还与相邻结构的形式和质量相关。若伸缩缝均按照最小宽度设置，在EL-centro波激励下，双向和三向输入时，1#梁和2#梁发生碰撞的时间延迟；双向输入使1#梁和3#梁发生碰撞的时间延迟，三向输入却使发生碰撞的时间提前。

图7　EL-centro波激励下竖向加速度响应 Fig.7 Vertical acceleration response under EL-centro excitation

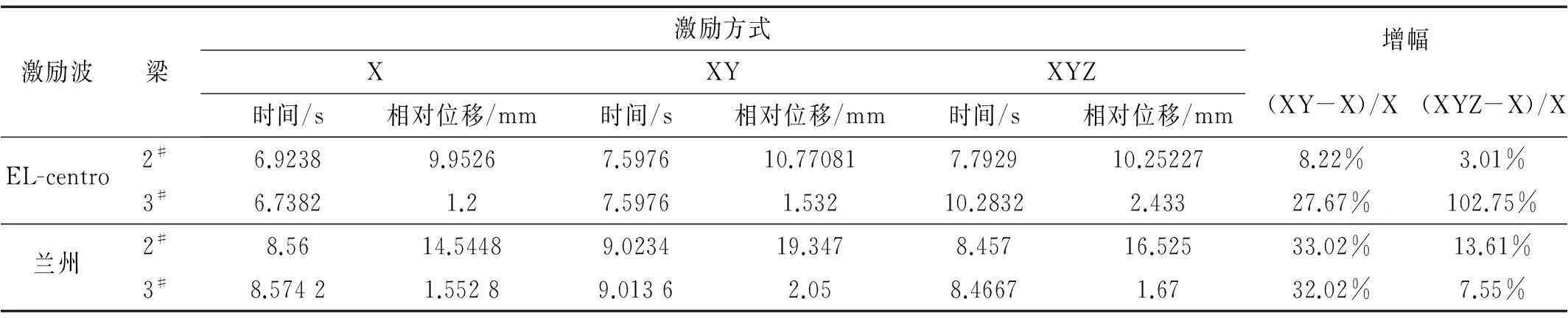
激励波梁激励方式XXYXYZ时间/s相对位移/mm时间/s相对位移/mm时间/s相对位移/mm增幅(XY-X)/X(XYZ-X)/XEL-centro2#6.92389.95267.597610.770817.792910.252278.22%3.01%3#6.73821.27.59761.53210.28322.43327.67%102.75%兰州2#8.5614.54489.023419.3478.45716.52533.02%13.61%3#8.57421.55289.01362.058.46671.6732.02%7.55%

EL-centro波激励下的2#伸缩缝处，三向输入应设置的最小伸缩缝宽度较双向输入增大；其他情况下，双向地震动输入较三向输入使该人字桥梁纵向梁之间更易发生碰撞。

3动力分析

采用通用有限元软件 ANSYS 建立人字曲线桥梁模型，1#异形梁建模采用梁格法，梁格分割箱梁的同时保证荷载的正确传递，分割后构件单元和刚性梁单元分别用Beam188和MPC184单元描述；2#和3#梁采用Beam188单元，墩采用Beam4单元。

3.1墩顶位移响应

图8　4 #墩与2 #墩顶横桥向相对位移 Fig.8 Transverse relative displacement to bridge between 4 #and 2 # pier top

图8给出EL-centro波激励下，主梁分支处4#墩与2#墩顶横桥向相对位移试验结果及数值模拟结果。由图知，数值模拟结果与试验值基本吻合，单向激励下，相对位移最大值为0.033 13 m，双向和三向激励下，相对位移最大值都为0.032 26 m，说明竖向分量输入对两墩横桥向相对位移无影响；单向激励下的相对位移值更大一些，表明人字桥梁分支处两墩设置防止横桥向发生撞击的初始间隙只需考虑直梁纵桥向激励的影响。

3.2桥墩内力响应

表7给出纵桥向墩底弯矩，可以看出，在两种波激励下，单向输入时纵桥向墩底弯矩最小，双向和三向输入使墩底纵桥向墩底弯矩增加；竖向分量输入对纵桥向墩底弯矩基本无影响；兰州波频谱分布对结构的影响和能量都比EL-centro波弱，激励下的墩底弯矩响应总体都比EL-centro波要小。

在单向输入时，6#墩为3#曲线梁的右侧边墩，弯矩最大，3#曲线梁中墩5#墩和另一边墩4#墩纵桥向墩底弯矩依次减小，1#主梁和2#分支直线梁墩底弯矩都相对较小，2#分支直线梁右侧边墩3#墩底弯矩最小。双向和三向输入时，2#墩底弯矩最大，4#墩次之，3#墩底弯矩最小。表明对于人字曲线桥梁，单向输入时曲梁墩底纵桥向墩底产生弯矩比直梁要大；双向和三向输入对分支直梁和分支曲梁的左侧边墩墩底弯矩影响最大，分叉曲梁的右侧边墩和中墩墩底弯矩响应强于分支直梁的右侧边墩。

表7　纵桥向墩底弯矩/kN·m

4结论

设计制作了几何相似比为 1/20 的人字曲线桥梁结构模型，进行了多维振动台试验，通过试验结果和数值计算分析，主要结论如下：

(1)桥墩顶纵桥向加速度响应不受竖向地震分量的影响；双向和三向激励都使分支曲线梁桥墩顶纵桥向加速度响应相对于单向激励降低，且降低幅度随着墩与台面正向角度的增加而增加。

(2)三向地震动输入使各梁跨中产生剧烈竖向加速度响应，分支曲梁跨中响应受水平输入的影响较分支直梁大，直梁部分受竖向地震动分量的影响最显著。

(3)双向和三向激励易使纵向梁体发生碰撞，影响程度视地震波输入及激励方向不同而有差异；主梁与分支直梁应设置的初始间隙应大于主梁与分支曲梁。

(4)主梁分支处的两桥墩，竖向分量地震波输入不影响其横桥向相对位移，横桥向初始间隙的设置只需考虑水平单向激励的影响。

(5)水平单向输入使分支曲线梁纵桥向墩底弯矩比直梁大；双向和三向激励对分支梁的左侧边墩墩底弯矩影响最大，竖向分量输入对纵桥向墩底弯矩无影响。

参考文献

[1]卢彭真，张俊平，赵人达.典型人字形桥梁模型试验研究与分析[J].工程力学,2008,25(3):139-143.

LU Peng-zhen,ZHANG Jun-ping, ZHAO Ren-da.Analysand study on model experiment of typical Y-Shape bridge[J].Engineering Mechanics,2008,25(3):139-143.

[2]Saiidi M S, Vosooghi A, Choi H, et al. Shake table studies and analysis of a two-span RC bridge model subjected to a fault rupture[J]. Journal of Bridge Engineering, 2013.

[3]Saiidi M S, Vosooghi A, Nelson R B. Shake-table studies of a four-span reinforced concrete bridge[J].Journal of Structural Engineering, 2012, 139(8): 1352-1361.

[4]宋旭明,戴公连,方淑君.三汊矶湘江大桥整体模型试验[J]. 中国公路学报,2009,22(1):53-59.

SONG Xu-ming,DAI Gong-lian,FANG Shu-jun.Total bridge model test of sanchaji Xiangjiang bridge[J].China Journal of Highway and Transport,2009,22(1):53-59.

[5]瞿伟廉,孙五一,周强.万州长江大桥欠质量模型振动台试验研究[J]. 武汉理工大学学报,2005,27(8):45-67.

QU Wei-lian,SUN Wu-yi,ZHOU Qiang.Shaking table test research on insufficient-mass model of Wanzhou yangtze river bridg[J].Journal of Wuhan University of Technology,2005,27(8):45-67.

[6]钟栋青,王曙光,刘伟庆.连续梁桥纵向减震性能振动台试验与理论分析[J].土木工程学报,2012,45(11):147-152.

ZHONG Dong-qing,WANG Shu-guang,LIU Wei-qing.Shaking table experimental study and theoretical analysis of the longitudinal seismic-reduced behavior of continuous-beam bridges[J]. China Civil Engineering Journal,2012,45(11):147-152.

[7]Williams D, Godden W. Seismie response of long curved bridge structures[J]. Experimental Model Studies. Earthquake Engineering and Structural Dynamics,1979.7:107-128.

[8]王蕾.大跨度刚构桥地震响应分析及振动台试验研究[D].北京：北京交通大学,2010.

[9]Wieser J, Zaghi A E, Maragakis M, et al. A Methodology for the experimental evaluation of seismic pounding at seat-type abutments of horizontally curved bridges[J]. Bridges, 2014, 10: 9780784412367.055.

[10]沈朝勇,周福霖,黄襄云,等. 动力试验模型用微粒混凝土的初步试验研究[J].广州大学学报:自然科学版,2005,3:249-253.

SHEN Chao-yong,ZHOU Fu-lin,HUANG Xiang-yun,et al. Experimental research on mircroconcrete used in dynamic test model[J].Journal of Guangzhou University:Natural Science Edition,2005,3:249-253.

[11]周颖，吕西林.建筑结构振动台模型试验方法与技术[M].北京：科学出版社，2012.

[12]Papazoglou A J, Elnashai A S. Analytical and field evidence of the damaging effect of vertical earthquake ground motion[J]. Earthquake Engineering and Structural Dynamics, 1996, 25(10): 1109-1138.

[13]Kunnath S K, Erduran E, Chai Y H, et al. Effect of near-fault vertical ground motions on seismic response of highway overcrossings[J]. Journal of Bridge Engineering,2008,13(3):282-290.

第一作者谢伟平男，教授，博士生导师，博士，1965年生

通信作者黄金男，硕士生，1990年生

第一作者胡均平男，博士，教授，博士生导师，1964年7月出生

通信作者李科军男，博士生，1984年4月生

邮箱:likejuncsu@126.com