基于Abaqus的水下结构声辐射仿真方法

吴健++李泽成++熊晨熙

摘要： 提出一种在Abaqus中直接完成辐射声场仿真的方法，该方法可大大减少流场网格层数.利用无限元的计算结果求解任意远处球形声场的声压；结合弹性球壳的解析解算例验证该方法的正确性，并将该方法拓展到细长型结构中.结果表明：基于Abaqus无限元的水下结构声辐射的计算方法简单、可行；采用有限元与无限元相结合的方法可以大幅度缩小流场区域.

关键词： 水下结构； 声学无限元； 声介质； 声辐射； 球壳

中图分类号： TB532文献标志码： B

0引言

随着现代潜艇隐身技术的发展，带肋圆柱壳体作为潜艇的典型结构形式，其在无限介质中的流固耦合振动和声辐射问题日益成为研究的热点.采用仿真分析的方式研究水下结构声辐射问题可节省大量的试验费用，是当前的主要研究方法.

一般来说，水下结构的振动声学分析方法主要有解析法和数值法2类.解析法只适用于计算少数具有正交曲面的弹性结构（如球面和圆柱面等结构）的辐射场.采用解析法求解复杂结构的声学问题很困难，因此对于一般形状的物体应采用数值法进行求解.目前，声辐射的数值法很多基于模态叠加法，由于高频模态较为密集且结构模态阻尼难以准确测量，因此直接法求解结构声辐射有很多优势.商德江[1]提出首先在有限元中计算模型在激励力作用下的流固耦合动力响应，再利用结构表面的位移作为边界元的边界条件，计算声学物理量的计算方法.姚雄亮等[2]将ANSYS与Sysnoise相结合对双层壳体水下振动和声辐射进行仿真分析，认为利用2种软件相结合的方法对水下复杂结构的振动和声辐射进行数值计算完全可行.缪旭弘等[3]通过Abaqus和声固耦合算法对双层圆柱壳的水下噪声辐射特性进行计算和分析，计算值与实验数据吻合较好.以上方法均采用声学无限元或边界阻抗技术的处理方式实现无限大流场，一般需要建立足够大的水体模型来满足声学边界条件，水体单元需要涵盖到声压分析位置，或者使用Sysnoise软件求解任意远场点的声压.

Abaqus具有较强的建模与计算分析能力，但在声学后处理方面稍显薄弱.本文提出一种在Abaqus中直接完成辐射声场仿真的方法，利用弹性球壳的解析解算例验证不同建模方式时声辐射结果的正确性.结果表明：Abaqus中的无限元技术可以采用较小流场进行水下结构振动分析，求解得到的任意远场点的声辐射结果精度满足分析要求.

1理论背景

1.1有限元方程

有限元对模型进行分析是通过对模型进行离散后求解波动方程和运动方程实现的.在流固耦合面上，结构振动会产生流体负载，而声压同时对结构产生附加力，所以必须同时计算结构动力方程和流体域的波动方程，用统一的矩阵形式表示为Ms

ρRf 0

Mf u¨

p¨+ Cs

0 0

Cf u·

p·+ Ks

0 -Rf

Kfu

p=Fs

0（1）式中：Ms为结构质量矩阵；Ks为结构刚度矩阵；Cs为结构阻尼矩阵；Mf为流体质量矩阵；Kf为流体刚度矩阵；Cf为声阻尼矩阵，Rf为流固面上的耦合矩阵；ρ为流体介质密度；u和p为节点的位移和声压向量；Fs为结构的载荷向量.用式（1）可以同时得到流固面上的位移和声压值.

1.2无限流场模拟

声波在有限流场中传播时，由于边界阻抗的存在，在流场的边界必然存在声波的反射.采用声学无限元技术后，由声学介质组成的流场能够满足在流场无穷远边界上的Sommerfield辐射条件lim rr→∞（pr+jkp）=0（2）2有限元建模

2.1网格划分

有限元分析中的网格划分好坏直接关系到模型计算的准确性.根据波动理论，单元长度的细化标准为在一个弯曲波波长内要有4个以上单元.板的弯曲波波长近似计算公式为r=δ212（1-μ2）（3）

λB=2πrCB/f（4）式中：r为板的惯性半径；δ为板厚；μ为泊松比；λB为弯曲波波长；CB为弯曲波波速；f为计算频率上限.为适应计算数据的分布特点，应在结构不同部位采用疏密变化的网格.

流体网格应保证每个声波波长内网格数量大于6个，同时流体与结构耦合面网格尺寸应与结构保持一致，水体单元采用声学单元模拟.

2.2声学无限元技术建模

声学无限元技术要求在结构中设置参考点作为声场分析的原点，一般应将无限元设置成外凸形状.在Abaqus中可以利用“skin”在水体外边界上定义无限元，并赋予“acoustic infinite”属性.在网格划分时采用相应的声学无限元单元，即完成无限元边界定义.结构表面与水体的接触面用关键字“TIE”实现，使用该关键字可以使水体与结构表面始终保持接触状态而不分离.[4]

2.3场点声压计算

通过声场分析插件“acousticVisualization”可将无限元的声压计算结果拓展到任意远球壳声场上[5]，目前仅支持基于直接法的稳态声振耦合计算结果文件，且结果文件中必须包含声学无限单元的法向矢量INFN，基于参考点的无限单元半径INFR和无限单元的压力系数PINF的输出结果.

3仿真方法验证

采用受法向简谐点集中力作用的弹性球壳在无限大流体中的结构声辐射作为考核算例，具体流体结构参数如下：球壳半径为0.5 m；球壳壁厚为0.001 m；球壳体密度为7 800 kg/m3；弹性模量为210 GPa；泊松比为0.3；损耗因子为0.02；流体密度为1 025 kg/m3；流体声速为1 500 m/s.

无限大流体中球壳的声辐射解析式为

p（r，θ，t）=-ρω2∞n=0Unrh（2）n（kr）kdh（2）n（x）dxx=kR·endprint

Pn（cos θ）eiωt（5）

式中：Unr为球壳法向振动位移的n号简正模的振幅；r为球壳半径；Pn（）为n阶勒让德多项式；h（2）n（）为第二类球汉克尔函数.

应用Abaqus程序计算流场辐射声压，两者相比较，考核计算方法和计算程序的正确性.

计算场点处的声源级（换算成距球心1 m处的声压级）Lp=20lgp（r，θ）1×10-6+20lg r（6）式中：（r，θ）为场点在以球心为原点的球坐标系中的坐标，见图1.

图 1球壳和坐标系

Fig.1Spherical shell and coordinate system

对该模型进行有限元建模，采用结构化有限元网格划分方法，结构网格和水体网格分别为四边形和六面体单元.根据式（2）和（3）求得本模型在400 Hz时的弯曲波波长为0.16 m.取一个波长内8个节点，即结构网格尺寸为0.02 m，共9 126个结构单元.水体厚度为0.02 m，网格尺寸为0.02 m，水体为1层单元，共28 087个声学单元和9 360个声学无限元单元，见图2.数值结果与解析结果的声源级比较见图3.各子图中2条曲线均几乎完全重合（微小差异是由于网格划分等数值离散引起的），说明本文所述的有限元加无限元的计算方法和计算程序是正确的.

图 2结构化有限元网格

Fig.2Structured finite element mesh

a）r=100，θ=π/2b）r=100，θ=0c）r=1，θ=π/2d）r=1，θ=0图 3声源级比较

Fig.3Acoustic source level comparisons

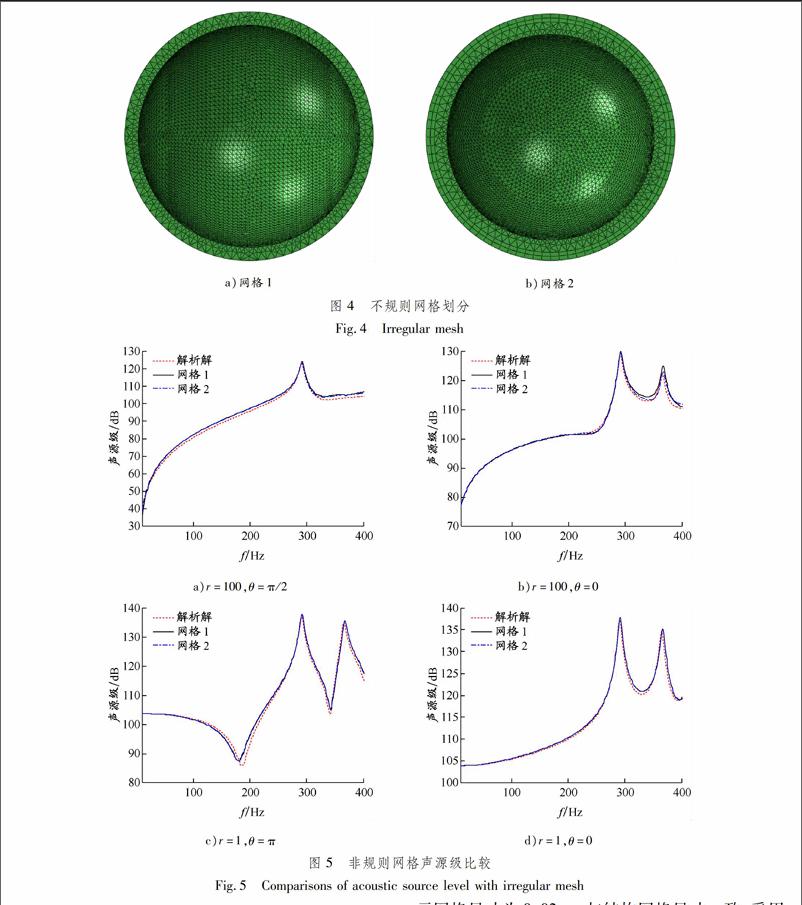
在实际问题仿真过程中，结构和水体模型往往难以划分结构化网格，且在声学无限单元中，无限方向上（参考点与无限元节点射线方向）的声场变化是通过一组包含10个9阶多项式的函数给出的[5]，在水体模型网格缩小后无限单元是影响计算速度的主要因素.对2种不同流场网格划分方式进行结果对比：网格1直接采用四面体网格，由细到粗过渡，内层网格尺寸为0.02 m，外层网格尺寸为0.04 m，共5 320个声学无限元单元；网格2将流体网格分为2部分，与结构接触部分采用四面体网格，在流体边界外侧采用结构化网格，且网格由内至外逐渐变粗，内层网格尺寸为0.02 m，外层网格尺寸为0.04 m，共2 946个声学无限单元.这2种网格划分方式均可明显减少无限元网格的数量.有限元模型见图4，数值仿真结果见图5.由此可知：采用网格1和2的划分方法，计算结果与解析解吻合仍然较好；100 m处声场计算结果中网格2划分方法精度要优于网格1划分方法，且这2种网格划分的计算时间都远低于结构化网格划分方式.因此，在分析复杂结构工程问题时建议采用网格2的网格划分方式.

a）网格1b）网格2图 4不规则网格划分

Fig.4Irregular mesh

a）r=100，θ=π/2b）r=100，θ=0c）r=1，θ=πd）r=1，θ=0图 5非规则网格声源级比较

Fig.5Comparisons of acoustic source level with irregular mesh

4细长结构声辐射分析

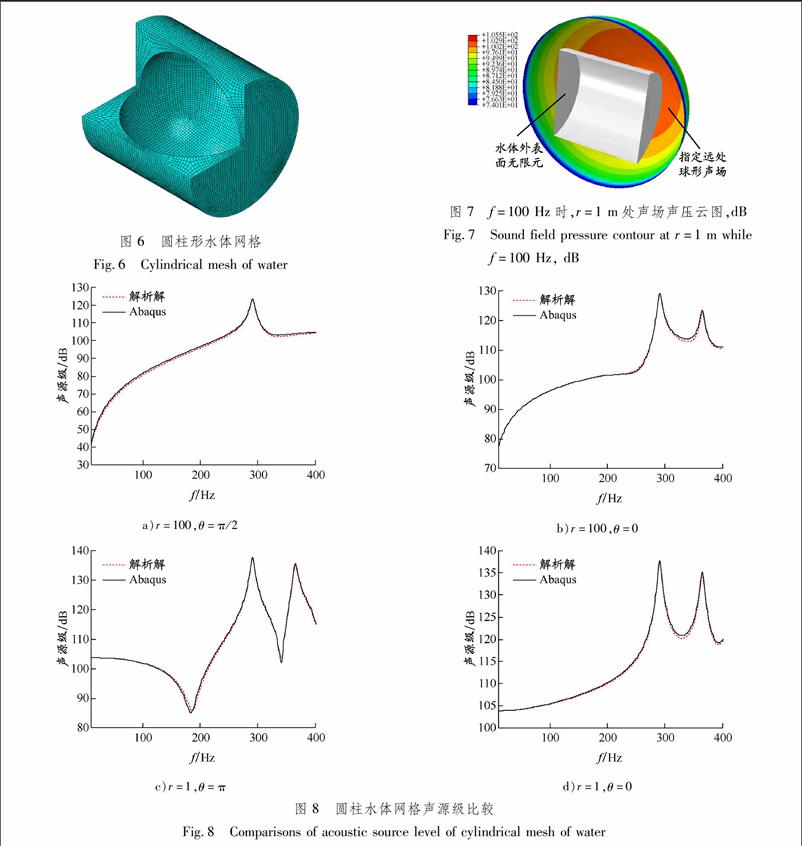
水下潜器如潜艇、鱼雷等一般为细长结构，采用有限元法进行声辐射分析时如果建立球形水体，水体部分会形成大量的网格，导致有限元法对硬件要求极高且计算频率上限较低.采用前文仿真方法，针对球壳结构模型建立圆柱水体求解结构声辐射.

水体边界与结构最小距离为0.04 m，水体有限元网格尺寸为0.02 m，与结构网格尺寸一致，采用结构化网格自动划分方式，网格见图6.根据无限元分析结果进行后处理，进一步拓展到1和100 m处声场声压见图7，分析结果见图8.有限元分析结果与理论结果吻合较好，说明这种求解方法对水体形状无特殊要求，因此计算细长结构声辐射时仅需建立完全包裹结构的圆柱水体单元.图 6圆柱形水体网格

Fig.6Cylindrical mesh of water图 7f=100 Hz时，r=1 m处声场声压云图，dB

Fig.7Sound field pressure contour at r=1 m while

f=100 Hz， dB

a）r=100，θ=π/2b）r=100，θ=0c）r=1，θ=πd）r=1，θ=0图 8圆柱水体网格声源级比较

Fig.8Comparisons of acoustic source level of cylindrical mesh of water

5结论

提出一种在Abaqus中有限元加无限元直接计算流固耦合结构声辐射的仿真方法，采用直接法进行稳态响应计算，能够求解任意距离处的声场分布，通过算例验证计算方法和计算程序的正确性，并给出提高计算效率的网格划分策略，得出以下结论.

1）该法在Abaqus中可完成任意距离的声辐射计算，计算过程简化，结果精度满足分析要求.

2）采用有限元加无限元的方法可以大幅度缩小流场，采用恰当的网格划分方法可以大大提高计算效率，特别有利于细长型水下结构的计算，降低硬件资源需求.参考文献：

[1]商德江. 复杂弹性壳体水下结构振动和声场特性研究[D]. 哈尔滨： 哈尔滨工程大学， 1999.

[2]姚熊亮， 杨娜娜， 陶景桥. 双层壳体水下振动和声辐射的仿真分析[J]. 哈尔滨工程大学学报， 2004， 25（2）： 136140.

YAO Xiongliang， YANG Nana， TAO Jingqiao. Numerical research on vibration and sound radiation of underwater double cylindrical shell[J]. J Harbin Eng Univ， 2004， 25（2）： 136140.（下转第65页）第24卷 第6期2015年12月计 算 机 辅 助 工 程Computer Aided EngineeringVol.24 No.6Dec. 2015endprint