平面应力问题新型广义有限元法
杨璞++牛红攀++肖世富
摘要: 结合广义有限元和理性有限元的优势,针对平面应力问题提出一种新型广义四边形单元.该单元考虑泊松效应,以节点位移自由度约束弹性力学平面应力方程的半解析解,构造单元位移模式的附加项,较准确地反映真实位移场,提高单元的计算精度.推导新型广义单元及其等参单元的形函数公式,设计分片试验和数值算例验证单元的精度.数值算例结果表明:在规则网格和非规则网格下新单元的计算精度均优于传统有限元和广义有限元.新单元具有精度高且易于程序实现的特点,可推广应用到实际工程的结构分析中.
关键词: 平面四边形单元; 等参元; 平面应力; 广义有限元; 形函数; 分片试验
中图分类号: O242.21文献标志码: A
0引言
有限元法的基本思想是在力学模型上将一个原来连续的物体离散为有限个单元,对每个单元选择一种简单的函数来表示单元内位移的分布规律,并按能量原理(变分原理)建立单元节点力和节点位移之间的关系,最后将所有单元集成并求解节点的位移.[1]
传统线性有限元直接以数学为基础采用双线性多项式构造形函数,其位移模式既没有考虑弹性力学控制方程,也不能反映不同自由度间位移的相互影响,单元精度较低.为改善计算精度,20世纪90年代钟万勰院士团队研发理性有限元,核心思想是从弹性力学出发建立位移模式,其插值函数的各项均来源于弹性力学精确解,有着明确的物理意义[27],但理性有限元形函数繁复,给实际操作带来很大困难[89].近年来,张洪武教授团队在理性有限元的基础上发展广义有限元方法,核心思想是改变传统有限元只利用单元节点同方向自由度的位移构造方式,而以单元所有节点自由度来构造单元位移[1011],其位移模式沿用传统有限元的多项式插值函数,未考虑弹性力学控制方程.
本文针对平面应力问题,提出一种新型广义四边形单元,综合考虑理性有限元和广义有限元的优势,从弹性力学平面应力方程出发建立形函数,并在不改变单元自由度的情况下为形函数引入位移附加项,提高单元计算精度.该新单元只在传统有限元形函数基础上增加位移附加项,程序操作简单易于实现.
1平面应力新型广义四边形单元
1.1一般单元
传统平面矩形单元为4个节点八自由度,见图1.
图 1标准的平面四边形单元
Fig.1Standard plane quadrilateral element
用4个节点位移表达的位移模式为
u=N1uI+N2uJ+N3uK+N4uL
v=N1vI+N2vJ+N3vK+N4vL
(1)其中,插值函数为双线性函数,N1=(1-ξ)(1-η)/4
N2=(1+ξ)(1-η)/4
N3=(1+ξ)(1+η)/4
N4=(1-ξ)(1+η)/4 (2)该形函数的构造局限于数学层面,位移模式只包含节点同方向自由度,计算精度较低.
由弹性力学理论的泊松效应可知,一个方向的变形将引起另一个方向的位移.设计开发新型平面四边形单元,考虑弹性体的泊松效应,由单元的所有自由度构造单元位移模式,即单元内任意一点的位移分量不仅与4个节点位移分量方向的节点自由度相关,而且与4个节点处位移分量方向正交的节点自由度相关.该开发思想与广义有限元[1011]一致,区别是在建立形函数时进一步借鉴理性有限元思想,在传统有限元位移模式的基础上,根据节点位移自由度约束弹性力学平面应力方程,确定单元位移模式的附加项.新平面四边形单元的位移模式既考虑节点上所有的自由度,又考虑弹性力学控制方程,能较准确反映真实位移场,因此可能有更高的计算精度.以下针对平面应力情况进行形函数构造.
对于式(1),节点自由度确定的单元节点边界条件为u(-1,-1)=uI,u(1,-1)=uJ,
u(1,1)=uK,u(-1,1)=uL
v(-1,-1)=vI,v(1,-1)=vJ,
v(1,1)=vK,u(-1,1)=vL (3)为考察一个自由度对另一自由度位移的影响,以第1个节点的x方向自由度u1为例,分析其他节点自由度固定、仅在节点I施加x方向位移uI时对y方向位移的贡献.满足图1节点位移的条件表达式为u1(-1,-1)=uI
u1(1,-1)=u1(1,1)=u1(-1,1)=0
v1(-1,-1)=v1(1,-1)=v1(1,1)=
v1(-1,1)=0 (4)线弹性平面应力问题的齐次位移平衡微分方程为
22ux2+(1-μ)2uy2+(1+μ)2vxy=0
(1-μ)2vx2+22vy2+(1+μ)2uxy=0
(5)取满足式(4)第一行方程的形函数基为u1(x,y)=uI(1-x)(1-y)/4 (6)将式(6)代入式(5)的第1个方程得2v1xy=0 (7)将式(6)代入式(5)的第2个方程且考虑节点边界条件得(1-μ)2v1x2+22v1y2+(1+μ)14uI=0
v1(-1,-1)=v1(1,-1)=v1(1,1)=
v1(-1,1)=0 (8)结合式(7)和式(8),假设第1个自由度uI产生的y方向的位移为v1(x,y)=b0+b1x+b2y+b3x2+b4y2 (9)代入式(8)得b1=b2=0
b3=-2b0/(μ+1)+uI/8
b4=-(μ-1)b0/(μ+1)-uI/8 (10)由于位移v1完全由节点位移uI引起,设b0=βuI,则 v1(x,y)=β+-2μ+1β+18x2+
-μ-1μ+1β-18y2uI (11)代入坐标0,0得v1(0,0)=βuI (12)式(12)表明:位移v1中的常数项是由于泊松效应,由单元节点自由度位移分量引起的单元中心点该位移分量正交方向上的位移.通过ANSYS有限元计算并采用响应面方法,拟合得到的β与泊松比μ的关系式为β=0.152 1+0.023 78μ (13)式(13)的数据拟合图见图2.endprint
图 2平面应力单元因数β与泊松比μ之间的关系
Fig.2Relationship between plane stress element factor β and Poisson ratio μ
将式(13)代入式(11)得v1(x,y)=(c1(1-x2)+c2(1-y2))uI (14)其中c1=2μ+1(0.152 1+0.023 78μ)-18
c2=μ-1μ+1(0.152 1+0.023 78μ)+18 (15)同理,其他自由度的位移可表示为v2(x,y)=-(c1(1-x2)+c2(1-y2))uJ
v3(x,y)=(c1(1-x2)+c2(1-y2))uK
v4(x,y)=-(c1(1-x2)+c2(1-y2))uL (16)施加x方向节点位移约束将产生y方向的位移,可以看作x方向位移对y方向位移的贡献.综合考虑4个节点的位移附加项可得到位移v的表达式为v=N1vI+N2vJ+N3vK+N4vL+
N5(uI+uK)+N6(uJ+uL) (17)其中N5=c1(1-x2)+c2(1-y2)
N6=-(c1(1-x2)+c2(1-y2)) (18)同理可得到水平位移u的表达式为u=N1uI+N2uJ+N3uK+N4uL+
N7(vI+vK)+N8(vJ+vL) (19)其中:N7=c2(1-x2)+c1(1-y2)
N8=-(c2(1-x2)+c1(1-y2)) (20)写成矩阵表达式为u
v=N1N7N2N8N3N7N4N8
N5N1N6N2N5N3N6N4·
[uIvIuJvJuKvKuLvL]T(21)可以证明:在各节点处,N1=N2=N3=N4=1,N5=N6=N7=N8=0,满足插值函数的Kronecker delta性质;单元中任一点N1+N2+N3+N4=1,N5+N6=0,N7+N8=0,满足插值函数的归一性质.
1.2等参单元
传统等参元中整体坐标与局部坐标的映射关系为x′=N1x′I+N2x′J+N3x′K+N4x′L
y′=N1y′I+N2y′J+N3y′K+N4y′L (22)式中:N1,N2,N3和N4为式(2)在局部坐标系下的表达式.根据第1.1节中的思路,平面应力问题新型广义等参元位移模式为
u′=N1u′I+N2u′J+N3u′K+N4uL+N9v′I+
N10v′J+N11v′K+N12v′L
v′=N1v′I+N2v′J+N3v′K+N4v′L+N5u′I+
N6u′J+N7u′K+N8u′L (23)
其中各附加等参形函数为N5=β1(c1(1-ξ2)+c2(1-η2))
N6=-β2(c1(1-ξ2)+c2(1-η2))
N7=β3(c1(1-ξ2)+c2(1-η2))
N8=-β4(c1(1-ξ2)+c2(1-η2))
N9=β1(c2(1-ξ2)+c1(1-η2))
N10=-β2(c2(1-ξ2)+c1(1-η2))
N11=β3(c2(1-ξ2)+c1(1-η2))
N12=-β4(c2(1-ξ2)+c1(1-η2)) (24)式中:βi为面积因数,与单元节点所围三角形面积相关.图3b中,定义SΔJKL,SΔKLI,SΔLIJ和SΔIJK分别为三角形JKL,KLI,LJK和IJK的面积,S为四边形总面积,则βi的具体表达式为β1=2SΔJKL/S
β2=2SΔKLI/S
β3=2SΔLIJ/S
β4=2SΔIJK/S (25)在标准单元中,β1=β2=β3=β4=1.至此,平面应力问题新型广义等参单元的位移函数已给出,求解过程与传统的等参元相同.
a)b)图 3新型4节点广义等参元
Fig.3New generalized 4nodes isoparametric element
2分片试验
对平面应力问题新型广义等参四边形单元的收敛性进行分片测试.分片单元见图4.刚体位移测试:假定刚体位移模式为u=1,v=1,即在所有外节点处u1=u2=u3=u4=1
v1=v2=v3=v4=1 (26)计算内部节点5~8的位移.计算结果见表1.
常应变测试:对边界上的节点给以常应变位移场 u=1+3x+y
v=2+x+3y (27)采用1个Gauss积分点方案,内部节点位移结果见表2.结果表明:新单元能通过刚体位移测试,在1个积分点条件下通过常应变测试.
图 4等参单元分片试验
Fig.4Isoparametric element patch test
表 1刚体位移分片测试结果
Tab.1Rigid body displacement patch test results节点坐标理论位移计算结果xyuvuv50.20.2111.001.0060.80.4111.001.0070.80.6111.001.0080.20.8111.001.00
表 2常应变分片测试结果
Tab.2Constant strain patch test results节点坐标理论位移计算结果xyuvuv50.20.21.82.81.802.8060.80.43.84.03.804.0070.80.64.04.64.004.6080.20.82.44.62.404.60
3单元基本变形模态endprint
为考察平面应力新型广义等参单元的基本变形模态,采用图5的矩形进行等参单元特征值分析.
图 5矩形等参单元几何尺寸
Fig.5Geometrical size of rectangle isoparametric element
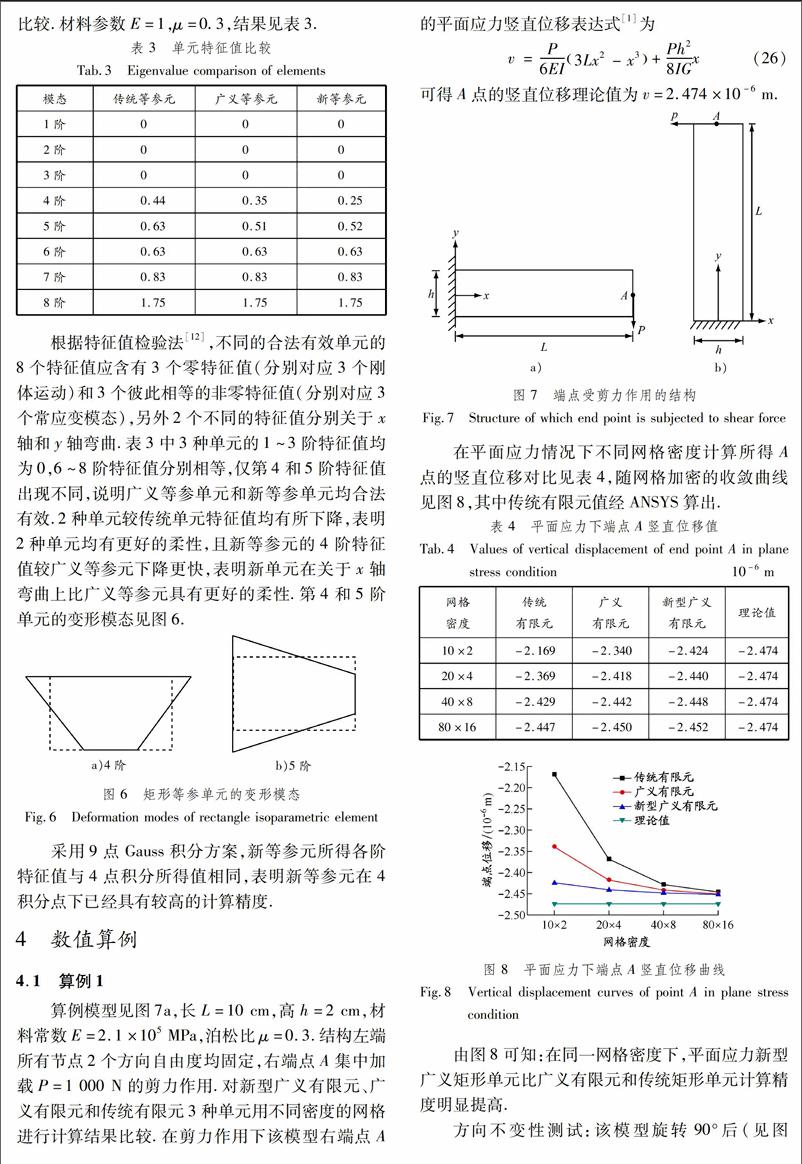
采用4点Gauss积分方案计算单元刚度矩阵特征值,并与广义等参元和传统等参元的特征值进行比较.材料参数E=1,μ=0.3,结果见表3.
表 3单元特征值比较
Tab.3Eigenvalue comparison of elements模态传统等参元广义等参元新等参元1阶0002阶0003阶0004阶 0.44 0.35 0.255阶 0.63 0.51 0.526阶 0.63 0.63 0.637阶 0.83 0.83 0.838阶 1.75 1.75 1.75
根据特征值检验法[12],不同的合法有效单元的8个特征值应含有3个零特征值(分别对应3个刚体运动)和3个彼此相等的非零特征值(分别对应3个常应变模态),另外2个不同的特征值分别关于x轴和y轴弯曲.表3中3种单元的1~3阶特征值均为0,6~8阶特征值分别相等,仅第4和5阶特征值出现不同,说明广义等参单元和新等参单元均合法有效.2种单元较传统单元特征值均有所下降,表明2种单元均有更好的柔性,且新等参元的4阶特征值较广义等参元下降更快,表明新单元在关于x轴弯曲上比广义等参元具有更好的柔性.第4和5阶单元的变形模态见图6.
a)4阶b)5阶图 6矩形等参单元的变形模态
Fig.6Deformation modes of rectangle isoparametric element
采用9点Gauss积分方案,新等参元所得各阶特征值与4点积分所得值相同,表明新等参元在4积分点下已经具有较高的计算精度.
4数值算例
4.1算例1
算例模型见图7a,长L=10 cm,高h=2 cm,材料常数E=2.1×105 MPa,泊松比μ=0.3.结构左端所有节点2个方向自由度均固定,右端点A集中加载P=1 000 N的剪力作用.对新型广义有限元、广义有限元和传统有限元3种单元用不同密度的网格进行计算结果比较.在剪力作用下该模型右端点A的平面应力竖直位移表达式[1]为v=P6EI3Lx2-x3+Ph28IGx (26)可得A点的竖直位移理论值为v=2.474×10-6 m.
a)b)图 7端点受剪力作用的结构
Fig.7Structure of which end point is subjected to shear force
在平面应力情况下不同网格密度计算所得A点的竖直位移对比见表4,随网格加密的收敛曲线见图8,其中传统有限元值经ANSYS算出.
表 4平面应力下端点A竖直位移值
Tab.4Values of vertical displacement of end point A in plane stress condition 10-6 m网格
密度传统
有限元广义
有限元新型广义
有限元理论值10×2-2.169-2.340-2.424-2.47420×4-2.369-2.418-2.440-2.47440×8-2.429-2.442-2.448-2.47480×16-2.447-2.450-2.452-2.474
图 8平面应力下端点A竖直位移曲线
Fig.8Vertical displacement curves of point A in plane stress condition
由图8可知:在同一网格密度下,平面应力新型广义矩形单元比广义有限元和传统矩形单元计算精度明显提高.
方向不变性测试:该模型旋转90°后(见图7b),所得结果与原结果相同,说明新单元具有方向不变性.
4.2算例2
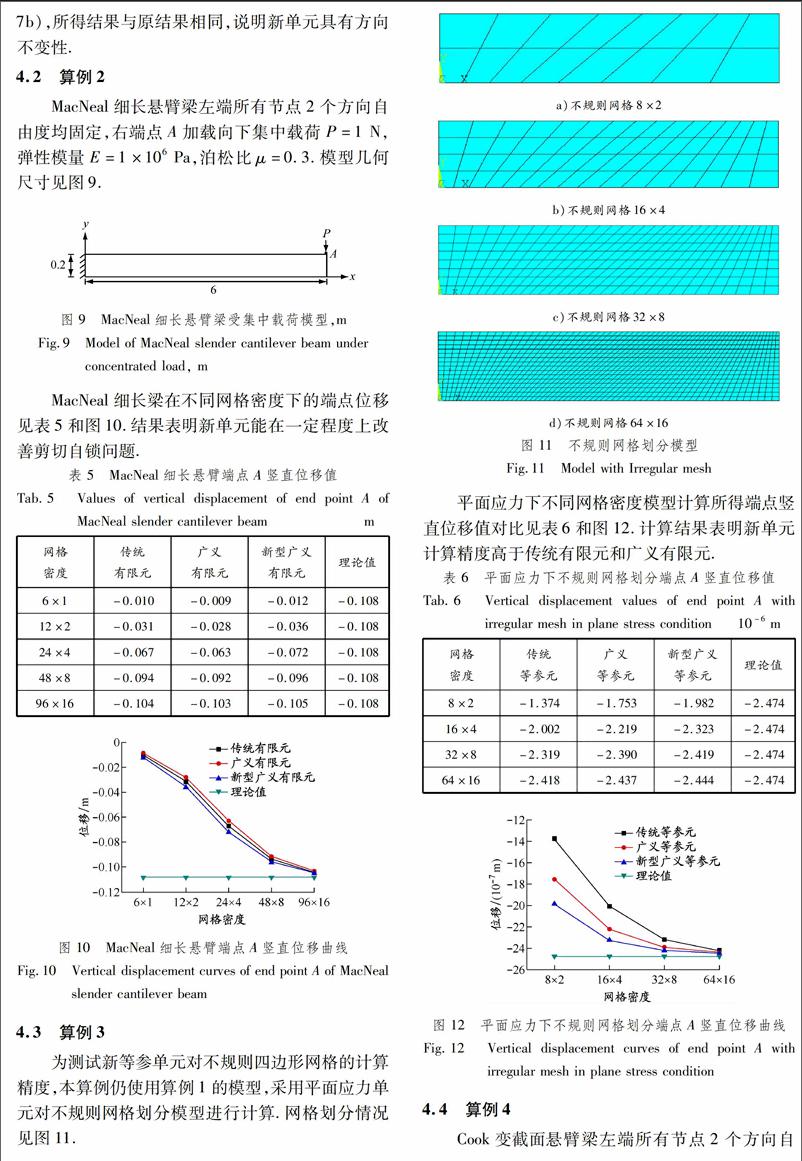
MacNeal细长悬臂梁左端所有节点2个方向自由度均固定,右端点A加载向下集中载荷P=1 N,弹性模量E=1×106 Pa,泊松比μ=0.3.模型几何尺寸见图9.
图 9MacNeal细长悬臂梁受集中载荷模型,m
Fig.9Model of MacNeal slender cantilever beam under
concentrated load, m
MacNeal细长梁在不同网格密度下的端点位移见表5和图10.结果表明新单元能在一定程度上改善剪切自锁问题.
表 5MacNeal细长悬臂端点A竖直位移值
Tab.5Values of vertical displacement of end point A of MacNeal slender cantilever beam m网格
密度传统
有限元广义
有限元新型广义
有限元理论值6×1-0.010-0.009-0.012-0.10812×2-0.031-0.028-0.036-0.10824×4-0.067-0.063-0.072-0.10848×8-0.094-0.092-0.096-0.10896×16-0.104-0.103-0.105-0.108
图 10MacNeal细长悬臂端点A竖直位移曲线
Fig.10Vertical displacement curves of end point A of MacNeal slender cantilever beamendprint
4.3算例3
为测试新等参单元对不规则四边形网格的计算精度,本算例仍使用算例1的模型,采用平面应力单元对不规则网格划分模型进行计算.网格划分情况见图11.a)不规则网格8×2
b)不规则网格16×4
c)不规则网格32×8
d)不规则网格64×16
图 11不规则网格划分模型
Fig.11Model with Irregular mesh
平面应力下不同网格密度模型计算所得端点竖直位移值对比见表6和图12.计算结果表明新单元计算精度高于传统有限元和广义有限元.
表 6平面应力下不规则网格划分端点A竖直位移值
Tab.6Vertical displacement values of end point A with irregular mesh in plane stress condition 10-6 m网格
密度传统
等参元广义
等参元新型广义
等参元理论值8×2-1.374-1.753-1.982-2.47416×4-2.002-2.219-2.323-2.47432×8-2.319-2.390-2.419-2.47464×16-2.418-2.437-2.444-2.474
图 12平面应力下不规则网格划分端点A竖直位移曲线
Fig.12Vertical displacement curves of end point A with irregular mesh in plane stress condition
4.4算例4
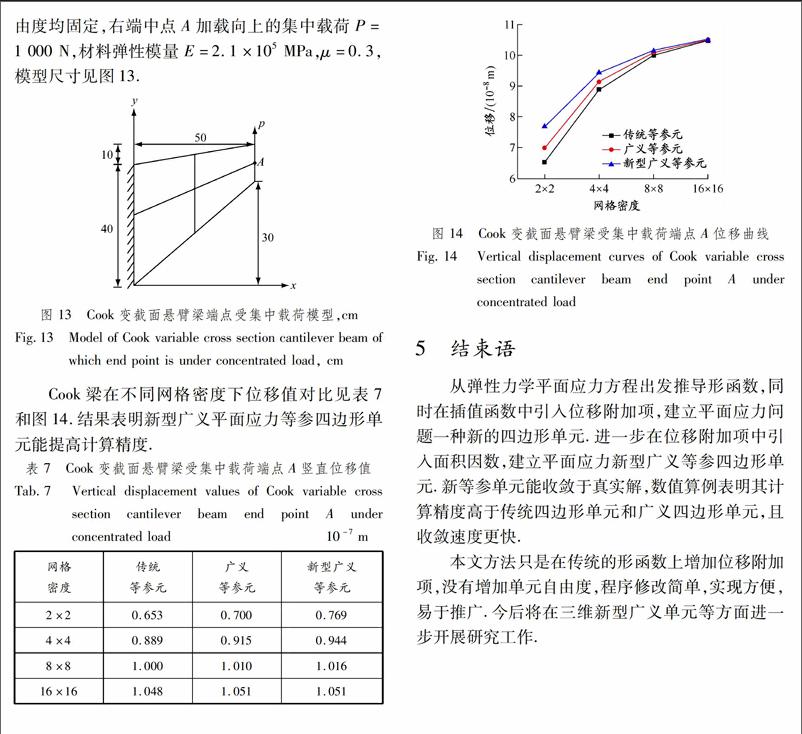
Cook变截面悬臂梁左端所有节点2个方向自由度均固定,右端中点A加载向上的集中载荷P=1 000 N,材料弹性模量E=2.1×105 MPa,μ=0.3,模型尺寸见图13.
图 13Cook变截面悬臂梁端点受集中载荷模型,cm
Fig.13Model of Cook variable cross section cantilever beam of which end point is under concentrated load, cm
Cook梁在不同网格密度下位移值对比见表7和图14.结果表明新型广义平面应力等参四边形单元能提高计算精度.
表 7Cook变截面悬臂梁受集中载荷端点A竖直位移值
Tab.7Vertical displacement values of Cook variable cross section cantilever beam end point A under concentrated load 10-7 m网格
密度传统
等参元广义
等参元新型广义
等参元2×20.6530.7000.7694×40.8890.9150.9448×81.0001.0101.01616×161.0481.0511.051图 14Cook变截面悬臂梁受集中载荷端点A位移曲线
Fig.14Vertical displacement curves of Cook variable cross section cantilever beam end point A under concentrated load
5结束语
从弹性力学平面应力方程出发推导形函数,同时在插值函数中引入位移附加项,建立平面应力问题一种新的四边形单元.进一步在位移附加项中引入面积因数,建立平面应力新型广义等参四边形单元.新等参单元能收敛于真实解,数值算例表明其计算精度高于传统四边形单元和广义四边形单元,且收敛速度更快.
本文方法只是在传统的形函数上增加位移附加项,没有增加单元自由度,程序修改简单,实现方便,易于推广.今后将在三维新型广义单元等方面进一步开展研究工作.
参考文献:
[1]王勖成. 有限元法[M]. 北京: 清华大学出版社, 2003.
[2]钟万勰, 纪峥. 理性有限元[J]. 计算结构力学及其应用, 1996, 13(1): 18.
ZHONG Wanxie, JI Zheng. Rational finite element RCQ8[J]. Comput Struct Mech & Appl, 1996, 13: 18.
[3]钟万勰, 纪峥. 平面理性元的收敛性证明[J]. 力学学报, 1997, 29(6): 676685.
ZHONG Wanxie, JI Zheng. Convergence proof of plane rational finite element[J]. Acta Mech Sinica, 1997, 13(6): 676685.
[4]纪峥, 钟万勰. 平面理性四节点及五节点四边形有限元[J]. 计算力学学报, 1997, 14(1): 1927.
JI Zheng, ZHONG Wanxie. Rational plane quadrilateral four and five nodes finite elements [J]. Chinese J Comput Mech, 1997, 14(1): 1927.
[5]王永富, 钟万勰. 平面八节点四边形理性元[J]. 固体力学学报, 2002, 23(1): 109113.
WANG Yongfu, ZHONG Wanxie. Plane 8 nodes rational finite element[J]. Acta Mech Solida Sinica, 2002, 23(1): 109113.
[6]纪峥, 刘泽佳, 赵伟. 平面理性八节点曲边四边形有限元RCQ8[J]. 大连理工大学学报, 2000, 40(1): 4044.
JI Zheng, LIU Zejia, ZHAO Wei. 8Node curve quadrilateral rational finite element [J]. J Dalian Univ Technol, 2000, 40(1): 4044.
[7]王永富, 钟万勰. 空间理性八节点块体元[J]. 应用力学学报, 2003, 20(3): 131135.
WANF Yongfu, ZHONG Wanxie. A rational hexahedron 8node finite element[J]. Chin J Appl Mech, 2003, 20(3): 131135.
[8]ZHANG H W, ZHENG Y G, WU J K, et al. Generalized fournode plane rectangular and quadrilateral elements and their applications in the multiscale analysis of heterogeneous structures[J]. Int J Multiscale Comput Eng, 2013, 11(1): 7191.(下转第71页)第24卷 第6期2015年12月计 算 机 辅 助 工 程Computer Aided EngineeringVol.24 No.6Dec. 2015endprint

