一题多解欣赏——第30届全国中学生物理竞赛复赛第2题评析

一题多解欣赏
——第30届全国中学生物理竞赛复赛第2题评析

陈东波

(绍兴市上虞中学浙江 绍兴312300)

收稿日期：(2014-06-10)

【题目】质量均为m的小球1和2，由一质量可忽略、长度为l的刚性轻杆连接，竖直地靠在墙角，小球1在杆的上端，如图1所示．假设墙和地面都是光滑的，初始时给小球2一个微小的向右的初速度．问在系统运动过程中，当杆和竖直墙之间的夹角等于何值时，小球1开始离开竖直墙面？

图1

参考解答：如图2，在小球1未离开竖直墙面之前，杆与竖直墙之间的夹角为θ时，小球1的坐标为

x1=0y1=lcosθ

(1)

小球2的坐标为

x2=lsinθy2=0

(2)

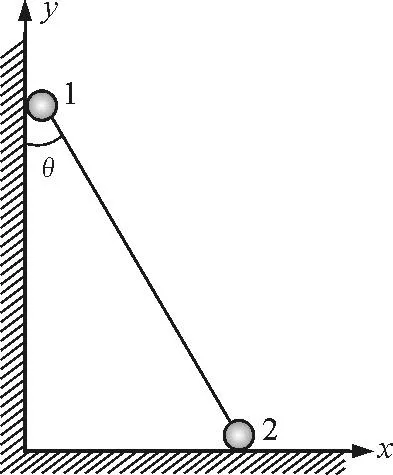
图2

小球1 的速度为

(3)

(4)

由机械能守恒定律，有

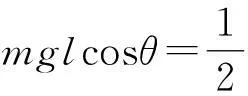
(5)

由式(5)得

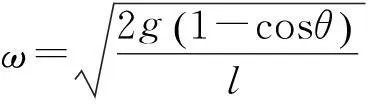
(6)

这里考虑到随着时间t的增加，θ变大，因此

ω>0．

系统质心C的x坐标为

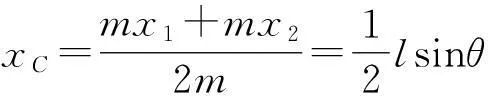
(7)

质心速度的x分量为

(8)

质心加速度的x分量为

(9)

由式(6)得

(10)

在得到上述结果时又利用了式(6)，把式(6)、(10)代入式(9)，得

(11)

设竖直墙面对小球1的正压力为T，质心C在x方向上的运动满足

T=2maCx

(12)

由式(12)可知，当aCx=0时，T=0.

此时，小球1开始离开竖直墙面，且θ=0为运动的初始时刻，即可得

此即小球1离开竖直墙面时，杆与墙面的夹角．

另解1

假设小球1被某种水平外力T束缚，使其只能在竖直平面内运动，则当杆与竖直墙面夹角为θ时，小球1与小球2的速度在沿杆方向的分速度必然有

v1cosθ=v2sinθ

由机械能守恒定律可得

由系统牛顿运动定律，小球1在水平方向所受合外力为零，则系统在水平方向所受合外力为

另解2

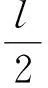
现假设墙面对小球1的弹力为T1，此时小球1沿竖直平面运动，水平方向合力为零，轻杆弹力必为

小球2沿水平平面运动，则水平地面对小球2的支持力为

图3

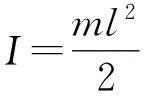
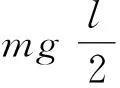
可得系统绕O转动的角加速度为

上式整理可得

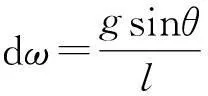
左右都乘以ω

考虑到在零时刻，ω和θ都为零，则有

在小球1离开墙面之前，考虑到直角三角形的中线性质，OP与竖直墙面的夹角始终等于轻杆与竖直墙面的夹角，则O点运动的角速度与角加速度大小都等于轻杆转动的角速度与角加速度的大小，则可以得到O的法向加速度与切向加速度分别为

当小球1离开墙面时，系统在水平方向不受外力，O点在水平方向加速度为零，即

a//=ansinθ-atcosθ=

化简可得

另解3

如另解2分析，O点运动的角速度大小等于轻杆转动的角速度ω，则有机械能守恒定律及柯尼系定律可得

可得O点运动所需向心力为

这个力等于系统所受重力、墙面弹力、地面弹力在沿OP方向分力的矢量和．再利用另解2中墙面弹力、地面弹力的关系可得

即

因为墙面弹力T1取负值不合题意，故可得答案．