从开普勒三定律谈谈行星椭圆轨道运动的基本参数

从开普勒三定律谈谈行星椭圆轨道运动的基本参数

史东升

(徐州市第一中学江苏 徐州221000)

摘 要：17世纪初德国天文学家开普勒总结出了行星运动的三大定律，在高中物理教学中为了简化把行星的椭圆轨道当成是圆轨道来处理．为了还原行星真实的运动规律，有必要把行星运动椭圆轨道运动的基本参数系统地总结一下．

关键词：开普勒三定律椭圆轨道面积速度周期速度曲率半径

收稿日期：(2014-11-19)

在竞赛试题中，学生经常会接触到物体按照椭圆轨道运动的情况，显然椭圆轨道比圆轨道要复杂一些，物体的速度如何变化，周期公式和圆轨道有什么异同，在不同位置的曲率半径如何计算等等.掌握了这些规律，可使考生高效准确地解题．首先来回顾一下开普勒行星运动三大定律．

1开普勒定律

1．1开普勒第一定律

1．2开普勒第二定律

1．3开普勒第三定律

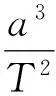
2行星椭圆轨道运动的基本参数

2．1面积速度

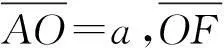
又由行星的机械能守恒

可得

所以面积速度

可见面积速度与中心天体的质量以及椭圆轨道的a和b有关，不同的行星轨道面积速度并不相同．

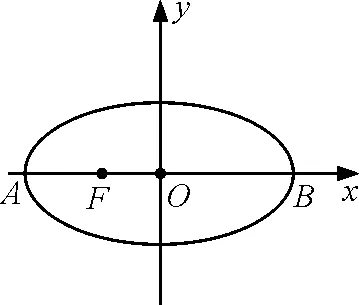
图1

2．2公转周期

我们知道椭圆的面积为πab，面积速度S与公转周期T的乘积等于椭圆面积，即

则公转周期

开普勒第三定律中的

可见定律中的k是一个只与中心天体有关的值，而与环绕天体无关．

2．3机械能

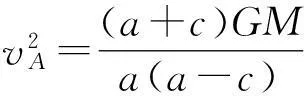
这个结果告诉我们如果选无穷远处引力势能为零，行星绕太阳做椭圆轨道运动的机械能

2．4速度大小

如果行星在椭圆轨道运动时到太阳的距离为r，太阳和行星的质量分别为M和m，引力势能

由机械能守恒

可以得到行星在任一位置的速度公式

可得在近日点速度

远日点速度

2．5曲率半径

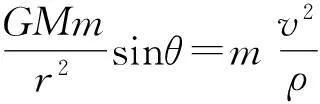
(1)

其中ρ为行星椭圆轨道在该点的曲率半径．因为行星绕太阳的角动量

L=mvrsinθ

(2)

在近日点A，角动量

L=mvA(a-c) =

代入(2)式得到

将结果代入(1)式，结合

得到行星椭圆轨道在任一位置的曲率半径

3实例分析

解：原来行星围绕恒星做匀速圆周运动

得到

所以此后行星将做以这颗恒星为一个焦点的椭圆轨道运动．行星原来的能量为

恒星质量突变后的能量为

根据前文所述，其面积速度

公转周期

在任一位置的速度大小

曲率半径

其中r为行星在椭圆轨道上运动时到恒星的距离．

【例2】如图2(a)所示，半径为R的空心圆环固定在滑块上，滑块放置在光滑的水平面上，滑块与圆环的总质量为M，质量为m的小球(视作质点)可在环内做无摩擦运动．开始时小球位于圆环最高点，环与小球均静止．在微小扰动下小球沿环下滑．

(1)试求小球相对地面的轨迹方程；

(2)求小球轨迹在图中A和B两处的曲率半径．

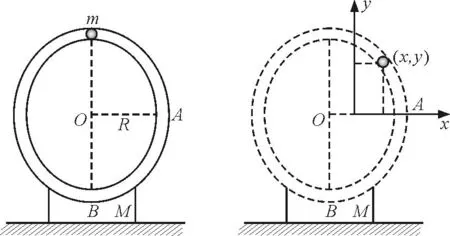
(a)　　　　　　　　　　　　(b)

解：(1)建立如图2(b)所示的坐标，设m的水平位移为x，m相对M的水平位移为s，由动量守恒得

0=mx+M(x-s)

其中

整理得到

(2)A点为椭圆“长轴”的端点，曲率半径为

B点为椭圆“短轴”端点，曲率半径为

可见从行星椭圆轨道运动得到的结果也可以应用到一般椭圆轨道上去，不过要特别注意条件上的一些变化．

4小结

本文从开普勒三定律出发，在机械能守恒和角动量守恒基本规律的指引下，借助于数学的手段系统地总结了行星绕太阳沿椭圆轨道运动的基本参数，希望在以后的解题中能对大家有所帮助．

参 考 文 献

1范小辉编著．新编高中物理奥赛实用题典．南京：南京师范大学出版社，2010