现行大学物理教材编写中的几个问题
现行大学物理教材编写中的几个问题
何志巍李春燕李 纯金仲辉
(中国农业大学理学院北京100083)
摘 要:从教材中常见的几个问题,包括物理概念分析、对应插图、公式推导及物理学史等方面,列举了大学物理教材分析中的一些亮点,对不同教材中相同问题的不同描述及数据分析等差异做了详细的论述,为广大教材编写者提供了一些思路.
关键词:教学内容教材插图公式物理学史
作者简介:何志巍(1979-),女,博士,副教授,主要从事大学物理教学与纳米材料科研工作.
收稿日期:(2014-09-15)
在编写大学基础物理教材的过程中,一定会广泛阅读他人编写的众多教材.在这些教材中,对一个物理概念会有不同的叙述,对同一个物理问题会有不同的解释.那么,怎样的叙述和解释才是最合理的呢?这就需要我们去分析和研究.另外,教材中的一些插图是否符合物理概念和原理、物理学史的叙述是否恰当,这也需要认真对待、去伪存真.虽说大学基础物理的教学内容都是比较成熟的,但由于它涉及到的知识面很广泛,且近些年物理学中包括光学、热学、量子等方面,尤其是电磁学在电子工业中的应用发展极其迅速.所以,编者需要付出艰辛的努力,才能将编写的教材精益求精,做到尽量减少不尽人意的内容.此外,我们应力求编写的教材中有其他教材中没有的教学内容,使所写的教材有不少新的亮点.以下我们举一些实例来说明.
1具体的物理问题
在薄膜等倾干涉和夫琅禾费衍射教学内容中都要涉及透镜的等光程性.如何证明它的等光程性呢?在不同的教材中对它有不同的叙述.例如,东南大学马文蔚等[1]编写的《物理学》是这样叙述的:平行光束通过透镜后,将会聚集于焦平面一亮点F(图1).这是由于某时刻平行光束波前5个点(图1中A,B,C,D,E各点)的相位相同,而到达焦平面后相位仍然相同,因而干涉加强.可见这些点到F的光程相等.
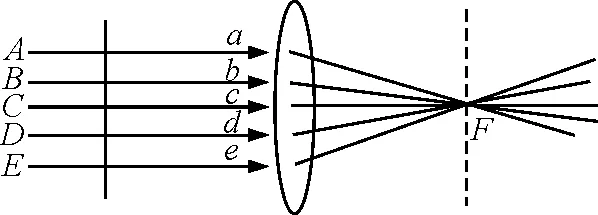
图1
清华大学张三慧[2]编写的《大学物理学》(第四册)是这样叙述的:平行光通过透镜后,各光线要会聚在焦点,形成亮点,这一事实说明,在焦点处各光线是同相的.
从表面上看,上述两本教材对透镜等光程的叙述基本上是相同的,但从叙述的逻辑上来说,后者恰当些.因为从实验结果(即F是亮点)来看,可以推断出,所有成像的光线的光程是相同的,相干叠加得到加强才得到亮点.而前者的叙述不仅不够严谨(如光线进入透镜内能否保持同相位),且逻辑上多少有些混乱,将因果关系颠倒了.
还有些教材的论证是有缺陷的,例如有一本教材是这样叙述的:当入射的平行光会聚于焦平面上F点(图1),虽然边缘光线(如AaF)比中部光线(如CcF)经过的几何路程长,但前者在透镜中的路程比后者的短,考虑到透镜的折射率大于1,可认为两光线经过透镜后光程的变化相等.从以上叙述内容来看,显然并没有论证这两条光线的光程是相等的,而仅仅是一种推想而已.在另一教材中叙述为:经过透镜边缘与透镜中心附近的光线的几何路程是不同的,例如CcF的路程比AaF短(图1),但前者在透镜的路程比后者长,而透镜材料的折射率大于1,如果折算成光程,通过计算可以证明两者的光程相等,使用透镜不会改变光程.从以上叙述内容来看,作者没有给出简明的方法来论证透镜的等光程性,如果学生问及如何计算,恐怕不是简单几句话可以说明白了!
2关于插图
2.1科纽棱镜插图
在紫外光谱仪中常使用科纽棱镜,这种棱镜由两块左(L)、右(R)旋石英晶体构成,如图2(a)所示,图中的虚线是晶体的光轴方向.
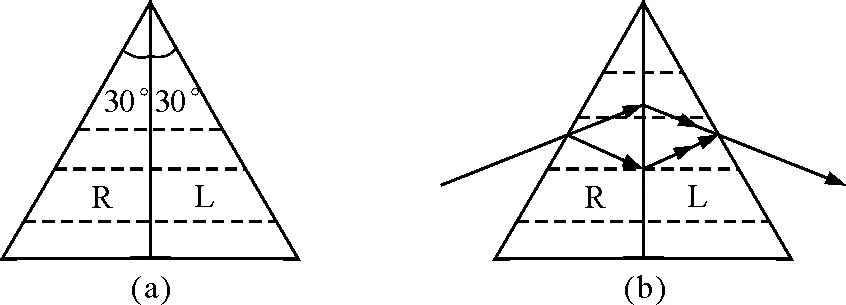
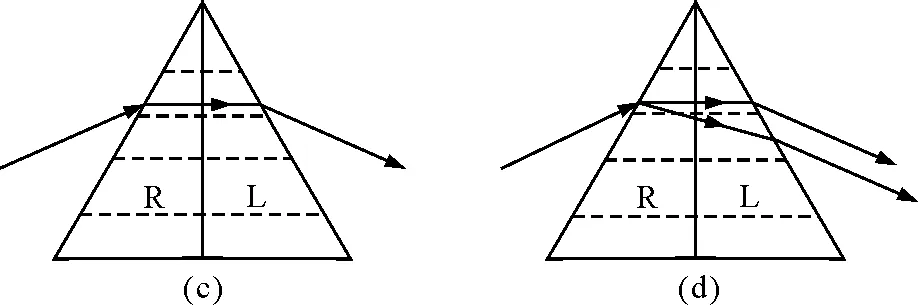
图2
现在需要指出的是,在一些光学教材中,有关科纽棱镜插图中的入射光线和出射光线的走向不相同.例如南开大学母国光[3]编写的《光学》中绘成图2(b)的形式;北京大学赵凯华[4]编写的《光学》中绘成图2(c)的形式;而华东师范大学姚启钧编写的《光学》中绘成图2(d)的形式,图中的两根出射光线好像是相互平行的(教材中没有明确说明是相互平行的).为什么对同一个物理现象有3种不同的插图?究竟哪一个插图合理呢?
棱镜是一种分光元件,我们当然希望一条入射的单色光入射至科纽棱镜,它的出射光也是一条单色光.由此看来,图2(b)和图2(c)似乎是合理的,但是图2(b)中棱镜内的两条光线的绘法显然是不合理的.因为对图2(b)中的界面AB来说,入射线和折射线均在入射面法线的同一侧.对于图2(c)来说,棱镜内的光线应有两条,而不是一条光线.通过计算可以证明,在一定条件下,图2(d)是合理的,因为出射的两条光线是近乎平行的.正因为这两条光线是平行的(它们间夹角极小),所以它们在经过透镜(或凹面镜)会聚于同处.这样对棱镜光谱仪来说,一束平行入射的单色光对应一条出射的单色谱线,这正是光谱仪所要求的.
2.2薄膜等厚干涉插图
薄膜等厚干涉的条纹定域在薄膜表面上.它的正确的插图应如图3(a)所示.但是在有一些教材(如马文蔚主编的《物理学》下册[6]和美国的哈里德等编写的《物理学基础》中的插图绘成了图3(b)和图3(c)的形式.这两个插图显然是错误的,因为插图中将在薄膜的两个表面上的反射光线绘成是平行的,它们将在无穷远处干涉,即干涉条纹定域在无穷远.

图3
2.3闭合磁畴的插图
为了说明铁磁质在未施加外磁场的情况下,不产生磁性而引入闭合磁畴的概念.有的教材将闭合磁畴绘成图4(a)的形式,有的教材绘成图4(b)的形式.哪一个图更显得合理呢?应该说图4(b)是合理的.因为它不存在退磁能,而图4(a)存在退磁能,所以相对于图4(a)中的单磁畴会出现不能相抵消的磁荷而存在能量更高的状态,故而不存在图4(a)形式的闭合畴.从实验观察到的闭合磁畴,证明了存在类似图4(b)形式的闭合磁畴.

图4
3关于公式推导的差异
3.1杨氏干涉条纹光程差公式
图5绘出了杨氏干涉装置的示意图.在推导杨氏干涉条纹宽度公式的过程中,在大多数的光学教材中采用光程差
(1)

图5
即认为r1=AP,或r1-AP≪λ.现在的问题是,由于可见光的波长是一个很小的量,在通常观察杨氏干涉条纹的实验装置数据(图5中D和d的数据)的条件下,r1-AP≪λ的条件是否满足呢?通过计算可证明,这个条件是不满足的.造成这种错误的原因何在呢?可能的原因是教材的编写者采用了某些国外教材中的计算方法.例如,美国的哈里德等编著的《物理学基础》中就是这样计算的.正确的计算方法如下
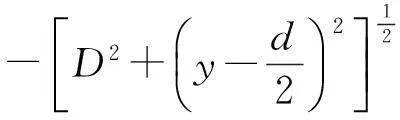
(2)
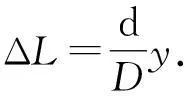
3.2薄膜干涉中光程差公式
薄膜干涉通常划分为薄膜两表面平行的等倾干涉6(a),它的干涉条纹定域在无穷远,以及劈尖状薄膜的等厚干涉6(b),它的干涉条纹定域在薄膜表面上.在国内的大多数教材中,都较详细地计算了等倾干涉6(a)情况下,在不计及半波损时反射光域1和2间的光程差为
ΔL=2nhcosr
(3)
而且不加任何说明,将上述公式直接作为劈尖薄膜的等厚干涉图6(b)中两反射光域1与2间的光程差.这种做法显然是不够严谨的.在笔者编写的教材中对此作了较为严谨的推导,说明了对于薄膜的等倾干涉和等厚干涉来说,在不计半波损的条件下,反射光域1与2之间有相同的光程差公式,即ΔL=2nhcosr.
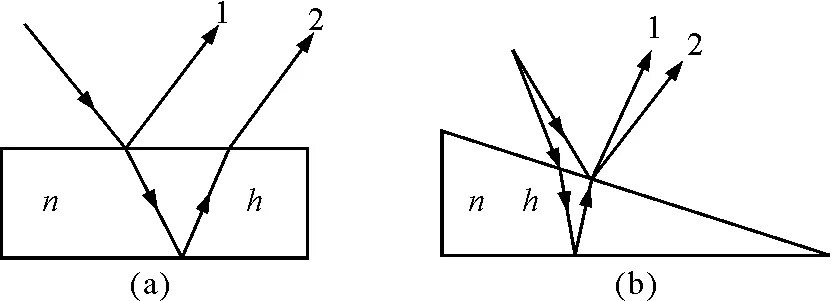
图6
4关于物理学史
在叙述一个物理规律或定律时,往往会涉及到它的历史问题.那么,一些教材中的叙述是否正确和全面呢?以下举几个例子来说明.
4.1库仑定律
该定律为:真空中两个静止点电荷之间的相互作用力与它们之间距离的平方成反比,与它们的电荷量的乘积成正比,作用力的方向沿两点电荷的连线上,同性电荷相斥、异性电荷相吸.在清华大学张三慧等编写的《大学物理学》(第三册)、东南大学马文蔚等编写的《物理学》(中册)和美国的哈里德等编写的《物理学基础》(最新的第六版)等教材都认为1785年法国的库仑用实验得出了库仑定律,这种说法是不够严谨的.事实是库仑在自制的扭秤实验中仅得出两点电荷间相互作用力与它们的间距的平方成反比的结论,而与它们的电荷量的乘积成正比是库仑所做的一个假设!库仑的这种假设来源于万有引力定律给予他的启发.
4.2法拉第电磁感应定律
上述这种情况在物理学中是不足为怪的,有不少物理学公式由理论分析得出,而无法用实验直接证明这些公式的正确性.这些公式的正确性,在于他们推导出一些公式,可由实验证明它们是正确的.
由以上讨论可看出,在编写教材时要特别谨慎,不要随意写出由实验表明如何得到的.因为这种表明未必符合史实.
4.3关于苹果落地启发牛顿发现万有引力定律的故事
在某些教材和一些科普性文章中说,牛顿大学毕业(1665年)后,在家乡躲避瘟疫时,偶然看到树上的苹果落地,启发他思考重力问题,并由此发现了万有引力定律.但是,这种说法不符合史实,因为经一些科学史专家研究发现,牛顿在生前从未在自己写的文章和与别人交谈过程中提及苹果落地的故事.有证据说明,这个故事是在牛顿去世不久,由他的亲属编造出来的,目的是提早牛顿发现万有引力定律的时间,以此保护牛顿对万有引力定律的发现权.现在我们知道,胡克、哈雷、惠更斯等物理学家虽然对万有引力定律的发现也有一定的贡献,但牛顿是万有引力定律的主要发现者是毫无疑问的.总之,如果在教材中写下牛顿受苹果落地的启发,发现了万有引力是极为不妥的,因为这不是史实.
限于文章的篇幅,有些内容没有讨论,例如,在不同的教材中,对同一个物理问题,给出的数据是很不相同的;对同一个物理概念给出了不同的叙述等等,这些问题都是需要推敲和仔细分析研究的.我们认为教学内容研究也是一种学术研究,只有认真做好这种学术研究才能编写出较好的教材.
参 考 文 献
1马文蔚,解希顺,周雨青.物理学(下册).北京:高等教育出版社,2006.100~ 101
2母国光,战元龄. 光学.北京:人民教育出版社,1981.210~ 211
3张三慧.大学物理学(第二册).北京:清华大学出版社,2009.187~ 188
4赵凯华.光学.北京:高等教育出版社,2006.108~ 109
5程守洙,江之永.普通物理学(第六版).北京:高等教育出版社,2006.136~ 137
6马文蔚,周雨青,解希顺.物理学教程(下册).北京:高等教育出版社,2006.180~182
7吴百诗.大学物理学(下册).北京:高等教育出版社,2004.189~190
8金仲辉,柴丽娜.大学基础物理学.北京:科学出版社,2010

