大学生物理竞赛试题赏析(Ⅲ)——电磁学部分

大学生物理竞赛试题赏析(Ⅲ)
——电磁学部分

刘家福张昌芳

(装甲兵工程学院物理室北京100072)

摘 要：首先对全国部分地区大学生物理竞赛中电磁学试题所占的比例进行统计，然后分析电磁学试题中各知识点的分布情况，最后对电磁学试题的方法进行剖析．

关键词：大学生物理竞赛电磁学试题基本要求

收稿日期：(2014-05-20)

自1984年以来，由北京物理学会和北京高校物理教学研究会举办的全国部分地区大学生物理竞赛从未间断，而且规模不断壮大，其考生成分、名称演化、影响和意义，已分别在前文[1,2]中述及．笔者关注该项赛事十余年，搜集、研究了其所有试题．本文是笔者对历届电磁学试题进行研究的总结，主要是对电磁学试题进行统计、分析，并对试题的典型方法进行剖析，希望能为日常教学、参赛选手的学习准备及竞赛辅导工作提供参考．

1电磁学试题及其在竞赛中的占比

电磁学问题通常与力学问题联系在一起，偶尔会涉及振动问题；《电磁学》与《光学》、《相对论》、《量子物理》等关系密切，甚至可以说是它们的基础．教育部教指委2010年编制发布的《理工科类大学物理课程教学基本要求》[3](以下简称《基本要求》)将大学物理课程分解为11个板块，《电磁学》为其第4板块．本文所采用试题均是以电磁现象、电磁性质和电磁物理量为研究对象，至于那些虽然有电磁学背景、以电磁学为基础，但不是以电磁物理量为研究目标的题目，不在本文考虑范围之内．

基于同样的原因[2]，本文所采用试题样本为非物理类A组试题，剔出了其中的实验题，而且将每一届的理论题总分数均折合为100分．

在表1中，我们列出了历届竞赛电磁学试题的总分数．其中，“沪津”指1988年上海、天津两市的大学生物理竞赛．

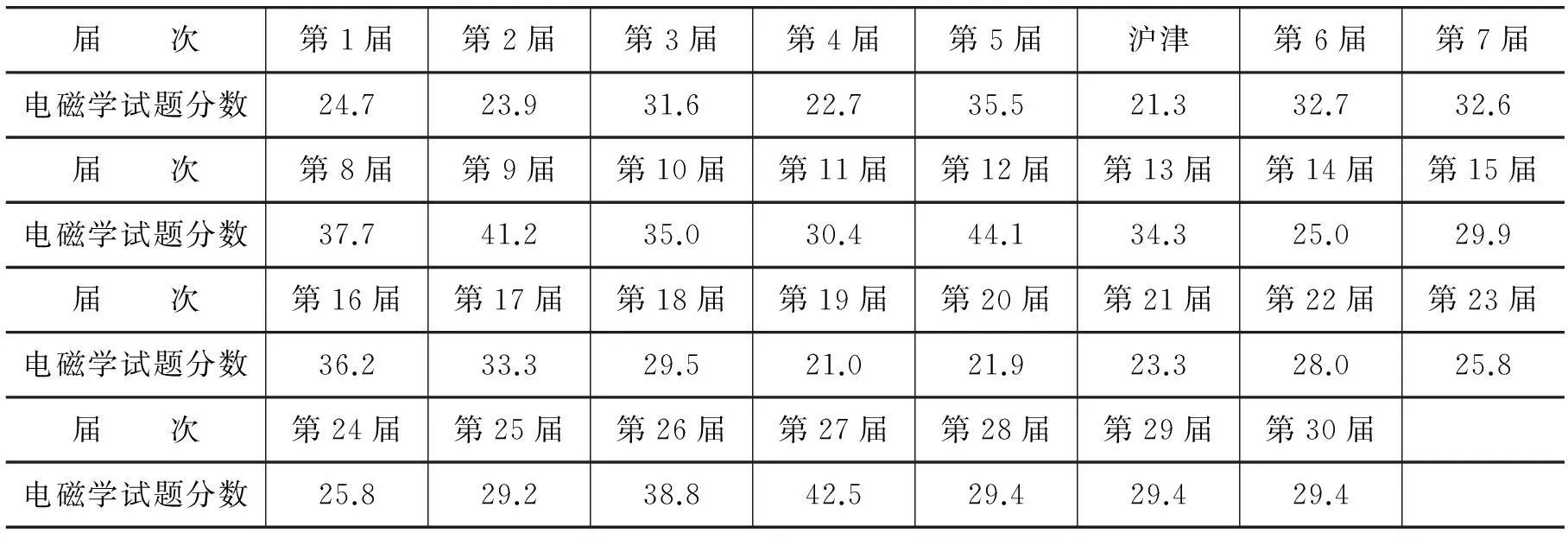
表1　历届大学生物理竞赛电磁学试题的总分数统计

从表1的数据看，虽然最高、最低占比相差一倍有余，但电磁学试题的占比总体上是比较稳定的．全部31套试题中，电磁学试题的平均占比为30.5%，标准偏差为6.3%．在《基本要求》中，建议《电磁学》授课不少于40学时，而整个课程不少于126学时，竞赛中电磁学试题的分数占比与《基本要求》建议的《电磁学》学时占比相当．

2电磁学试题各知识点的分布

《基本要求》将《电磁学》内容分解为A和B两类(A类为核心内容，本科生学习大学物理课程应达到的最低要求；B类为扩展内容，体现加强基础教育，增强学生发展潜力)共28条．在31套试题中，有2条A类知识点(电场强度和电势的关系、静电场的环路定理；电场和磁场的能量)和5条B类知识点(电介质的极化及其描述；物质的磁性、顺磁质、抗磁质、铁磁质；麦克斯韦方程组的微分形式；边界条件；超导体的电磁性质)没有直接考核，表2列出了其他各条内容在历届竞赛中所占比重的平均值．

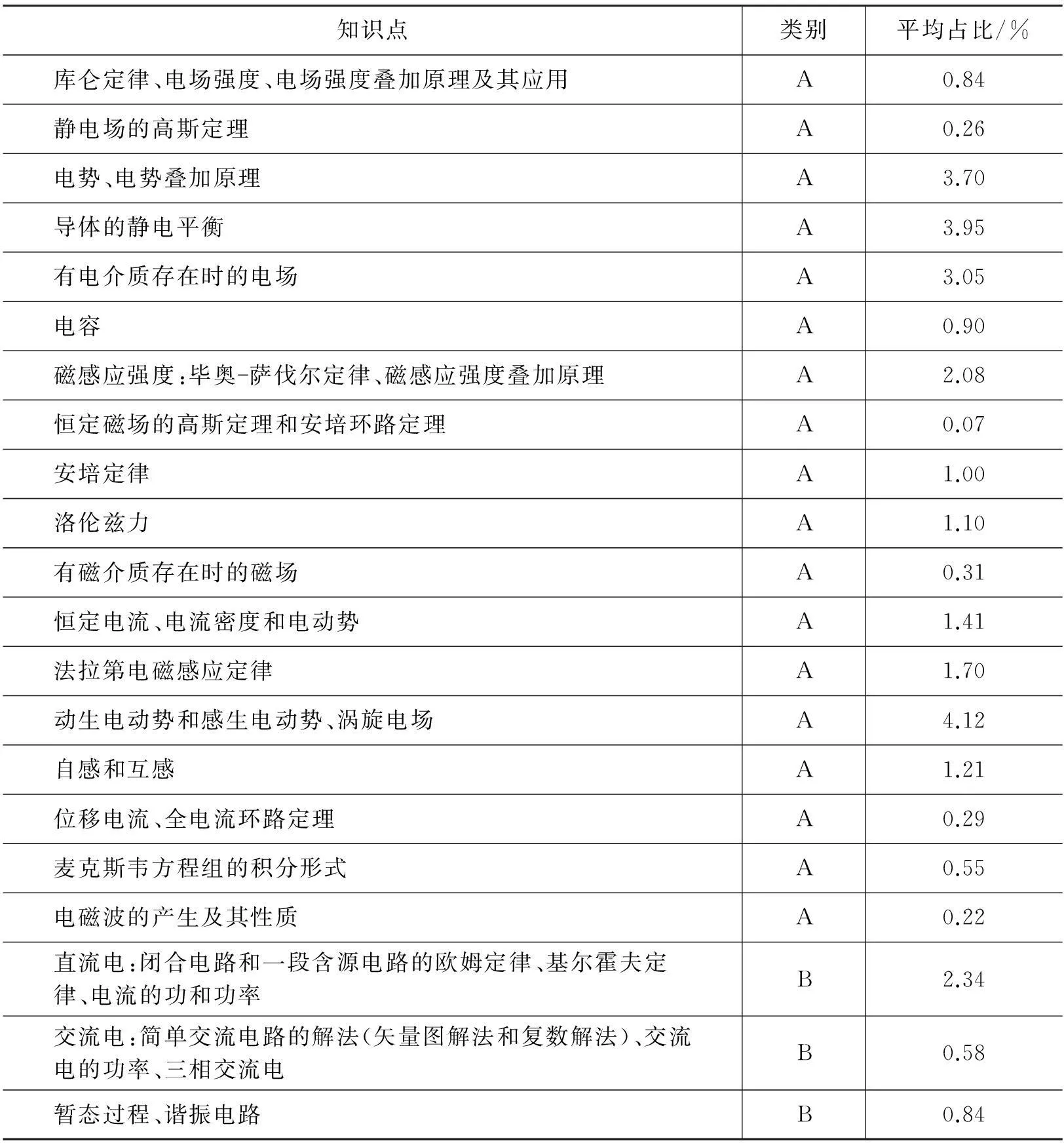
表2　《电磁学》各知识点在竞赛试题中的平均占比

统计发现，除了第18和第20届外，“感应电动势”和“导体的静电平衡”出现在各届的竞赛试题中，各出现18次，在历届试题中的平均占比分别为4.12%和3.95%．另外占比较高的是“真空中静电场的电势”问题和“有电介质存在时的静电场”问题．虽然“直流电”属于B类，平均占比达到2.34%，但是很多届的“直流电”问题考核的是等效电阻的求解，虽与中学物理有衔接，也涉及到一些方法，但与《基本要求》倡导的“增强学生发展潜力”的精神存在一定的差距．

3电磁学试题的方法

纵观30年的竞赛，绝大多数电磁学试题都是纯理论性的，几乎没有与日常生活、工程技术、科学前沿相联系的试题．而且，绝大部分电磁学试题可用逻辑分析的方法求解，即根据已知条件，利用一些物理原理和数学工具，演绎、推理出所要求的结果．

在电磁学试题中，也有一些题目比较灵活，有的需要一定的技巧，有的需要综合性分析，还有的体现了高等数学的思想．

3.1电磁学试题中的技巧

3.1.1补偿法的应用

高斯定理是描述静电场性质的重要定理，具有普遍性意义．在电荷分布具有简单的对称性(球对称性、轴对称性或面对称性)的情况下，可以用其来分析电场强度(及电势)的分布．但是，有的问题中电荷的分布不具有这样简单的对称性．如图1所示[4]，在半径为R1、电荷体密度为ρ的均匀带电球体中，有一个半径为R2的球形空腔，空腔中心相对球体中心的位置矢量为r0，要求球形空腔内任一点的电场强度和空腔中心处的电势．

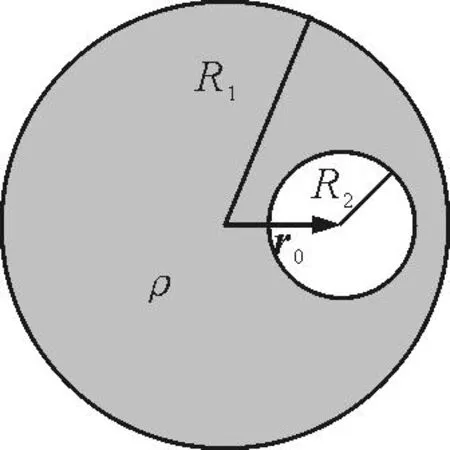
图1

这个问题中，电荷的分布就不具有球对称性．为了求解这个问题，需要在空腔内补上体密度为ρ的均匀电荷分布，同时补上体密度为-ρ的均匀电荷分布．如此一来，就可以利用高斯定理分别求出半径为R1、电荷密度为ρ的均匀带电球体及球形空腔处半径为R2、电荷密度为-ρ的均匀带电球体在空腔内任一点产生的场强及在空腔中心处产生的电势，然后再利用叠加原理得到最终结果．

这个问题使我们很自然地想起另外一个问题：在半径为R1，电流密度为j的无限长载流圆柱中，有一个半径为R2的无限长圆柱形空腔(轴相互平行)，求空腔内某点的磁感应强度．

这个问题的求解需要用到安培环路定理，由于电流的分布不具有简单的轴对称性，需要在空腔内补上电流，处理方法与上述方法完全类似．有趣的是，上述球形空腔内的电场是均匀的，这个圆柱形空腔内的磁场也是均匀的．

在圆柱区域内，平行于轴向均匀分布的磁场，当磁感应强度随时间变化时，可以利用

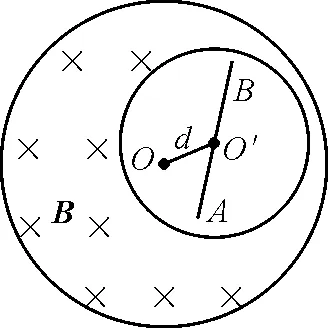
图2

为了求解此题，将空腔部分看作磁感应强度分别为B和-B的均匀磁场的叠加，于是整个磁场可以看作以过O点垂直于纸面的直线为轴的圆柱内的均匀磁场B和以过O′点垂直于纸面的直线为轴的圆柱内的均匀磁场-B的叠加，金属棍上的感生电动势εAB就是B变化产生的感生电动势ε1和-B变化产生的感生电动势ε2的代数和．其中，均匀磁场-B随时间的变化产生的感生电场E2垂直于金属棍，ε2=0．磁感应强度为B的均匀磁场产生的感生电动势ε1的分析见下一小节．

第25届竞赛的第18题[5]也同样用到补偿法求涡旋电场，在此不再赘述．

3.1.2辅助法的应用

在中学阶段学习几何时，我们不得不习惯于画辅助线，一条恰当的辅助线可以使几何难题瞬间变得简单．在电磁学中，也不乏利用辅助线求解问题的例子．

在上一个问题中，为了求出感生电动势ε1，如果按部就班地先求出磁感应强度为B的均匀磁场随时间变化产生的涡旋电场Ei的分布，再将Ei沿金属棍AB积分，这样做比较棘手(因为金属棍上不同线元处Ei的大小、方向不尽相同)．

如图3所示，作两条辅助线分别连接OA和OB，此时OA，AB，BO构成闭合回路．在OA，BO上，Ei与线元垂直，该闭合回路上的感生电动势即为ε1．而闭合回路OABO上的感生电动势可利用法拉第电磁感应定律很容易地求出．

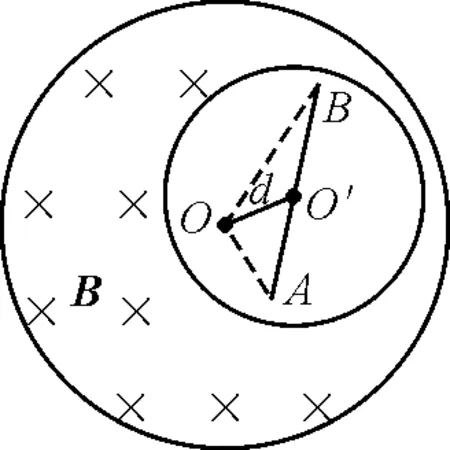
图3

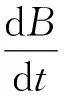
图4

这个问题中，虽然均匀磁场B对称地分布在圆形区域内，其随时间的变化产生的涡旋电场Ei的分布很容易得出，但由于MN上不同线元处Ei的大小、方向不尽相同，欲利用积分的方法达到目的，也是比较棘手的．如果作3条辅助线分别连接圆心和M，N及棒的中点，这个问题就迎刃而解了．

3.1.3等效法的应用

所谓等效法，就是在不影响问题的物理本质的情况下，将问题简化处理，找到解决问题的途径．

图5(a)所示的电阻丝网络[5]，水平和竖直的每一小段、三段斜电阻丝的每一段的电阻同为r，要求两个端点A，B间等效电阻R．

笔者刚接触到这个电阻丝网络时，也感到其复杂．经过仔细研究后，我们发现，按图5(b)的方法分解，如果将B′，C′接到一个电源的两极，则D，E两点的电位相等，即最右边两个图可以不予考虑．B′，C′间的等效电阻为rB′C′=r，rB′C′与rAC串联后再与rAB并联即为A，B间的等效电阻R．

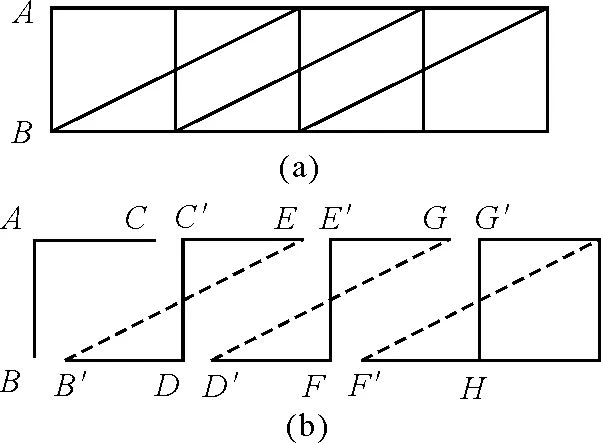
图5

另一个比较复杂的电阻丝网络如图6(a)所示[4]，3个半径相同的均匀导体圆环两两正交，各交点处彼此连结，每个圆环的电阻均为R，要求A，B间的等效电阻RAB和A，C间的等效电阻RAC．

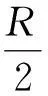
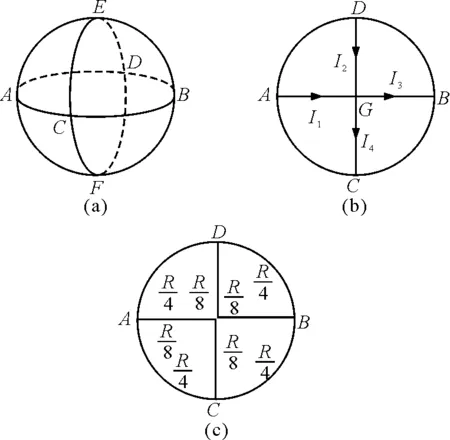
图6

为了求RAC，设想将A，C点接在电源的两极，从电流分布看，ACBDA环面的上、下两半是对称的，电路是完全一样的，因此可作图6(b)所示的叠合(图中G代表E，F两点的叠合)．图中电流间应有

I1=I4，I2=I3，这样就可以认为I1和I4独立于I2和I3而不在G点交汇，该电路于是可进一步等效为图6(c)所示的电路．如此，即可得到RAC．

3.2电磁学试题中的综合性分析方法

我们通常遇到的物理问题一般比较简单，可以很容易地看出因果关系、已知条件与待求结果之间的路径很明晰．但有些问题却不是这么简单．

图7所示的是两个同心相对放置的均匀带电的半球面[4]，它们的半径分别为R1和R2，电荷面密度分别为σ1和σ2，满足关系σ1R1=-σ2R2．要求证明小球面所对的圆截面S为等势面，并计算这个等势面的电势值．

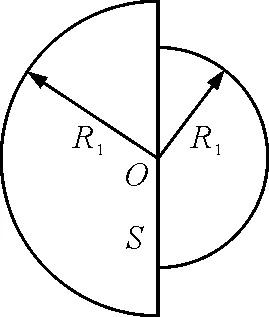
图7

如果能够证明S为等势面，这个电势值就很好求了，它就是球心O的电势．本题的关键是如何证明S为等势面．

按照逻辑性思维分析，在S上任意取一点求其电势，如果所得的值与点的位置没有关系，那就说明S是一个等势面．但此路不通．

我们改变思维的方向：若要证明S为等势面，只要证明S面上的电场强度与S面垂直即可；若要证明S面上的场强与S面垂直，只要知道两个半球面在S上独立产生的场强即可；最理想的情况，如果一个均匀带电的半球面在其大圆面上任一点的场强与大圆面垂直，那可就太棒了！是垂直吗？利用反证法，假设不垂直，那么导致的结果将是“一个均匀带电的球面在球面内产生的场强不为零”，这是错误的．这个错误说明了：一个均匀带电的半球面在其大圆面上任一点的场强与大圆面垂直；进而，两个半球面在S产生的合场强与S面垂直；再进而，S是一个等势面！

我们把从终点出发，往回找理由，让最后的理由与已知条件相吻合的思维方法称为综合性分析方法．这样的思维方法，不仅在电磁学中用到，在力学中同样有用，是各类证明题的通用方法．除了学习、研究外，这种思维模式对个人的成长、成才、成名也有十分重要的意义．

3.3电磁学试题中的数学思想

第7届竞赛有这么一个题目[4]：图8所示的电阻网络是由n个相同的单元重复连结而成，为使A，B间的等效电阻RAB与单元数n无关，求Rx的取值．

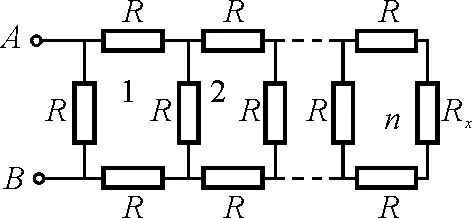
图8

既然RAB与单元数n无关，那么，当n=1和n=0时，A，B间的等效电阻值相等．或者，稍麻烦一点儿，取n=2和n=1时，A和B间的等效电阻值相等．Rx即可解出．

笔者当初分析这个问题时，设计了另外一个类似的问题：如图9所示，n个相同的单元重复连结而成的电阻网络，A，B间的等效电阻RAB与单元数n是什么关系？当n→∞时，RAB为何值？

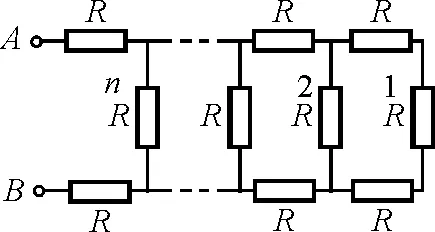
图9

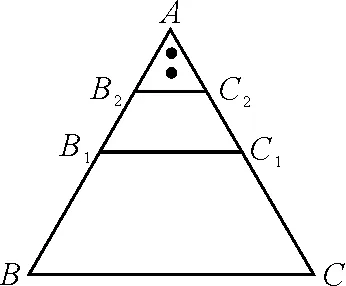
图10

笔者研究这个问题时，又联想到第15届竞赛的一个力学问题[6]：如图10所示，ABC为等边三角形，连接AB边、AC边的中点B1，C1，再连接AB1，AC1的中点B2，C2，…，如此继续下去，构成无限内接等边三角形系列．设所有线段的质量线密度相等，BC边的质量为m，长度为a，求等边三角形系列的总质量和系统质心与BC边的距离．

我们发现，这两个问题蕴含了数学中“极限”的思想，利用极限思想，其解唾手可得，有兴趣的读者可参阅文献[7]．

4结语

本文对全国部分地区大学生物理竞赛电磁学试题进行了统计，分析了各条知识的占比情况，剖析了典型的解题方法．电磁学试题要求考生具有较好的数学能力，涉及的方法与技巧较多．我们也希望在以后的竞赛中，命题组能够多设计一些与生活实际、工程技术或科学前沿相联系的试题，以培育学生的科学素养，增强他们的发展潜力．

参 考 文 献

1刘家福，张昌芳. 大学生物理竞赛及其试题特色. 物理与工程，2008，18(4)：65

2刘家福，张昌芳.大学生物理竞赛试题赏析(Ⅰ)——力学部分.物理通报，2014(10)：54～56

3教育部高等学校物理学与天文学教学指导委员会物理基础课程教学指导分委员会. 理工科类大学物理课程教学基本要求(2010年版).北京：高等教育出版社，2010. 1

4工科物理编辑部. 全国部分地区非物理类专业大学生物理竞赛题解汇编(第1～13届). 北京：工科物理，1997. 35，92，101，45，73

5北京物理学会. 第25届全国部分地区大学生物理竞赛试卷.2008.5,3

6工科物理编辑部. 全国部分地区非物理类专业大学生物理竞赛题解(第15届). 北京：工科物理，1998. 2，4

7汪斌，刘家福. 数列的极限及其应用分析. 数学的实践与认识，2006，36(8)：367