推导匀强电场中导体球的电荷面密度的简单方法

推导匀强电场中导体球的电荷面
密度的简单方法

郑 金

(凌源市职教中心辽宁 朝阳122500)

摘 要：通过推导一个数学结论和电偶极子的场强公式，利用均匀带电球体内部场强公式、等量异号电荷模型、镜像电荷模型和偶极子模型以及等效法和叠加法，对匀强电场中导体球的电荷面密度的关系式给出两种巧妙的推导方法.

关键词：月牙形导体球等效法电荷面密度

收稿日期：(2014-11-14)

对于匀强电场中的导体球的电荷面密度关系式，在电动力学教材和一些物理文献中，是利用拉普拉斯方程和勒让德函数进行推导的，比较高深.下面利用一些等效物理模型和有关数学知识，对匀强电场中的导体球感应电荷面密度关系式给出两种简单的推导方法.

首先推导一个简单的数学结论.如图1(a)所示，两个大小相等的圆不重合，相交于两点M和N，设直线OA偏离中轴线的角度为θ，两个圆心错开的距离为d，月牙弦的长度为h=AB=OA-OB，其最大值为d，最小值为零. 弦长h随直线OA的偏角θ而变化，θ越大，对应的弦长越小，那么弦长h与最大弦长d和偏角θ的数量关系是什么呢？

相交弦同侧的优弧与劣弧围成一个月牙形.两圆心O1与O2连线的中点为O，过点O作径向直线OA交优弧于点A，交劣弧于点B，把线段AB称为月牙弦.

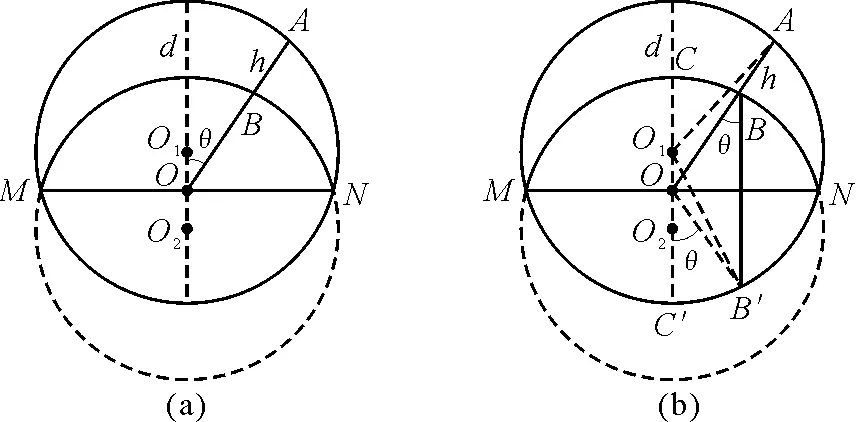
图1

为了求弦长h，需分别求出OA和OB的长度，可通过构造两个三角形利用余弦定理来求.如图1(b)所示，连接O1A，得到一个三角形O1OA，其中半径R=O1A所对的角度即直线OA与月牙形的中轴线的夹角为θ；两圆的公共弦为MN，劣弧MCN与劣弧MC′N关于直线MN对称，过点B作MN的垂线，与劣弧MC′N交于点B′，连接OB′，则OB=OB′，由对称性可知OB′与OC′的夹角也为θ.连接O1B′，又得到一个三角形O1OB′，其中半径R=O1B′所对的角度为180°-θ.

设OO1=l，则O1O2=d=2l.对三角形O1OA和O1OB′分别由余弦定理得

R2=l2+OA-OA·2lcosθ

R2=l2+OB′+OB′·2lcosθ

两式联立可得

OA-OB′=2lcosθ

由于

OB′=OB2l=d

所以月牙形的弦长为

h=AB=dcosθ

结论:两个重合的圆错开距离d而形成月牙形，若过两圆心连线中点的直线与月牙形中轴线的夹角为θ，则月牙形截得直线的长度即月牙弦的长度为h=dcosθ，是余弦函数.

该数学结论对于空间月牙体同样适用.下面利用这个结论推导匀强电场中导体球的电荷面密度.

【例1】如图2(a)所示，在电场强度为E0的匀强电场中，放着一个半径为R的金属球.若球面上的一点A对应的半径与场强正方向的夹角为θ，求金属球表面的感应电荷面密度σ与角度θ的关系式.

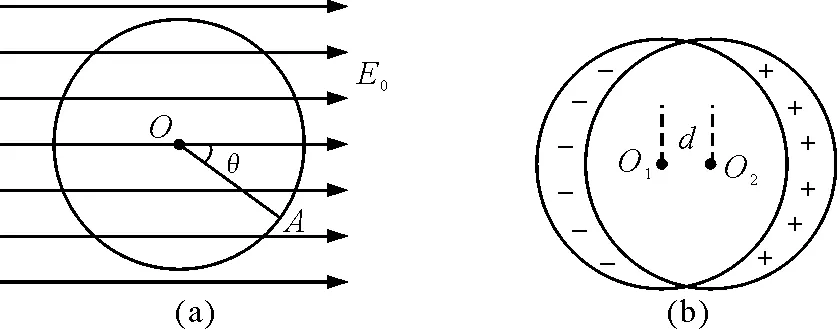
图2

解法1:利用数学结论和均匀带电球体模型

对于在匀强电场中的金属球，左侧表面出现负电荷，右侧表面出现正电荷，球内合场强为零，即球面感应电荷在球内产生匀强电场，场强大小也为E0，但方向相反.因此可利用两个大小相同的均匀带有等量异号电荷的球体交叠来构建匀强电场中导体球的等效模型，即分别在两个半径为R的绝缘球内均匀分布等量异号电荷，左球带负电，右球带正电，设想将两球互相交叠放入匀强电场中，球心不重合，而是沿电场方向稍微错开距离d，如图2(b)所示，两球重叠部分正负电荷中和而形成电中性的空腔，即空腔内的电荷体密度为零；在边缘形成两个月牙体，其中电荷按原密度均匀分布.

当d→0时，空腔趋近于半径为R的球体，月牙体几乎趋近于两个半球的表面.这与原题中的物理模型在空间几何图形上是等效的；虽然月牙体均匀带电，但由于月牙体的厚度不均匀，因此离中轴线越近，电荷量越大，这与匀强电场中的导体球表面感应电荷的分布情况相一致，所以两个物理模型在电荷分布趋势及对称性上是等效的.

可以证明，对于半径为R，均匀带电Q的球体内部距球心为r处的场强公式为

再推导两个大小相同的均匀带电的球体叠加区域的场强公式.如图3(a)所示，设左、右两球所带的电荷量分别为-Q和+Q，可认为分别集中于球心O1和O2的点电荷，在重叠区域任取一点P，对两个球心的矢径分别为r1和r2，方向都指向点P，则负电荷在P点产生的场强矢量为

正电荷在P点产生的场强矢量为

由矢量三角形可知点P处的合场强为

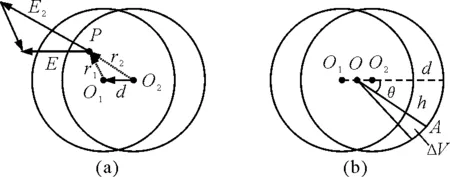
图3

由于两球心连线O2O1对应的矢量d1的大小恒定，方向恒定，则场强E恒定，表明在两球体重叠区域的电场为匀强电场，即两个月牙形带电体在空腔内产生匀强电场，方向与外电场相反，使叠加区域内的合场强为零，这与匀强电场中的导体球内合场强为零的情况完全一致，因此两个物理模型是等效的.

由

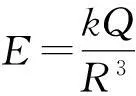
可知两绝缘球所带的电荷量大小为

则电荷体密度为

可用微元法求电荷密度，如图3(b)所示，月牙体所截得中轴线的长度即月牙体的最大厚度为d，过两球心连线O1O2的中点O作直线与月牙体的中轴线的夹角为θ，在其一边附近作一立体角元dΩ，对应的微小锥体在月牙体内截取一段小柱体ΔV，设其底面积为ΔS，则其体积为ΔV=ΔS·h.只要求出厚度h与最大厚度d和偏角θ的数量关系，就可求出电荷密度.

由月牙形厚度公式可知，在图3(b)中月牙体的厚度随偏角变化的关系式为

h=dcosθ

则立体角元在月牙体内截得小柱体的体积为

ΔV=ΔS·dcosθ

因此小柱体所带的电荷量为

ΔQ=ρΔV

所以该处的电荷面密度为

当两球心很近时，即d→0时，重叠区域趋近于球体，则直线OA与月牙形的中轴线的夹角趋近于球的半径与外场强正方向的夹角，所以金属球表面的感应电荷面密度与角度θ的关系式

解法2:利用像电荷模型和电偶极子模型

如图4(a)所示，一电偶极子的电偶极矩表示为p=ql，点P到偶极子中心O的距离为r，r与l的夹角为θ.在r≫l时，可求出P点的电场强度E在OP方向的分量Er.

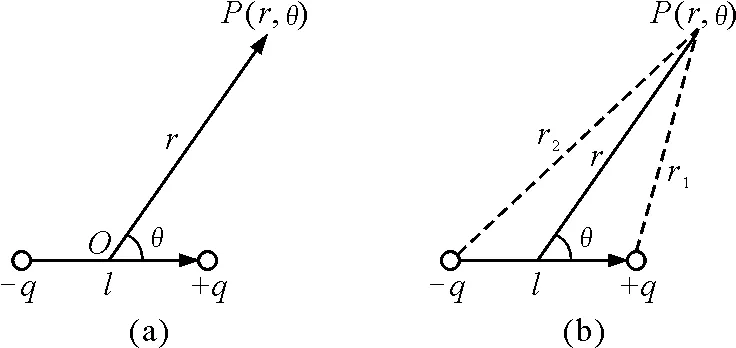
图4

如图4(b)所示，设两个点电荷到P点的距离分别为r1和r2，可知P点的电势为

由于r≫l，则

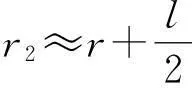
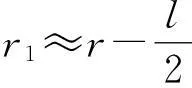
因此

r2-r1≈lcosθ

r2·r1≈r2

所以

可知P点的电场强度E在OP方向的分量为

如图5所示，两个点电荷q和-q分别放在过球心O的直线上关于球心对称的位置，到球心的距离为a，a很大，q也很大，则在球心附近区域产生的电场近似为匀强电场，由点电荷场强公式和电场叠加可知场强大小为

为了使该物理模型与例题中的物理模型等效，那么场强应为

E=EO

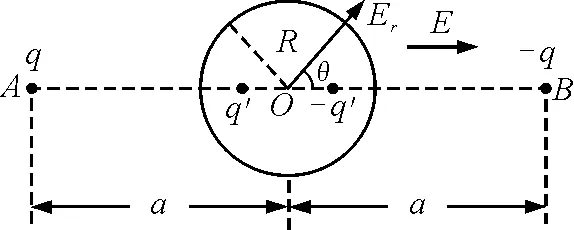
图5

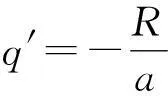
由一对等量异号点电荷±q组成的带电体系，若它们之间的距离l比场点到它们中点的距离r小得多，则把这种带电体系叫做电偶极子.偶极子在球面上任意点P产生的法向场强为

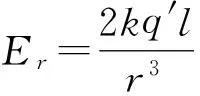
式中

r=R

则

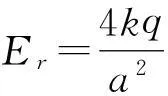
由于处于静电平衡状态导体表面的场强为4πkσ，则球面上P点的场强为

Er+EOcosθ=4πkσ

而

因此

2EOcosθ+EOcosθ=4πkσ

所以

角度θ是球面上的某点对应的半径与匀强电场正方向的夹角，对于一定的角度θ，电荷面密度相同的各点分布在球面的同一圆周上.

参 考 文 献

1沈晨.专题17——静电场：原理与方法.中学物理教学参考，2005(11)：53，56

2赵凯华，陈熙谋.电磁学(上册).北京：高等教育出版社，1988.43

3王浩川，等.构建一般化电荷模型求解静电物理问题.物理通报，2014(6)：72