例析磁感应强度及面积同时变化时磁通量的计算
例析磁感应强度及面积同时变化
时磁通量的计算
邓雪益
(睢宁高级中学北校江苏 徐州221200)
收稿日期:(2015-04-21)
磁通量及磁通量的变化概念抽象,一直是高中物理电磁感应方面的重难点.它可能会在不同情况下被要求计算,这给很多学生带来不小的难度.通常情况下,根据其公式Φ=BS,高中阶段大都仅限于B和S恒定或其中一个量变化的情况.但是,随着近几年高中物理逐步加大对学生微元累加(微积分)思想的培养,使得B和S同时变化时,计算磁通量及磁通量变化的题目屡见不鲜,这无疑给学生带来了更大的解题难度.面对这样的情况,笔者通过对一道相关题目的讨论和分析,初步总结出:面对B和S同时变化时,对磁通量及磁通量变化进行计算的几种处理方案.具体讨论过程如下.
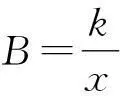
A.线圈穿过磁场的过程中感应电流的大小逐渐增大
C.线圈穿过磁场的过程中通过导线横截面的电荷量为零
D.穿过磁场的过程中磁通量最大为2ka
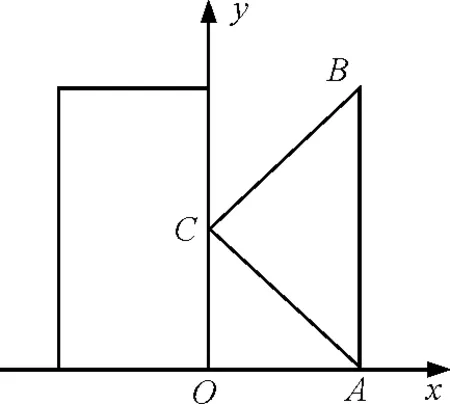
图1
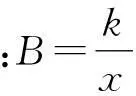
解析:线圈穿过磁场的过程中,感应电动势E=BLv,根据欧姆定律可得感应电流大小
另外,由几何关系知,切割边运动距离为x时,L=2x,解得
为定值.又由题意可知,线框运动距离为a时磁通量最大(此时磁通量积累最多),用时
先得到
又因为
联立得
消去R得到
ΔΦ=Φm-0=2ka
即磁通量最大为2ka,D选项正确.
思路二:联立电动势的两种计算式,变形后两边进行累加
解析:由法拉第电磁感应定律得
又根据导体棒切割产生感应电动势
E=BLv
联立得
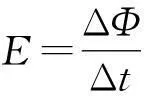
变式
ΔΦ=BLvΔt
进一步表示为
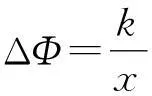
根据微元累加的观点对两边进行累加,其中对的累加变成末状态的磁通量Φ,对的累加成为线框的位移,由思路一可知,累加到a时有
Φ=Φm=2ka
思路三:利用数学基本定积分思路,列出磁通量函数方程式,对位移进行定积分
解析:根据题意可得出函数
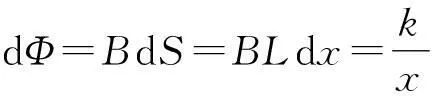
积分式
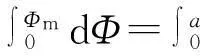
积分得
Φm=2ka
思路四:同样利用数学基本定积分,列出列出磁通量函数方程式,对面积进行定积分
解析:根据题意可得函数
dΦ=BdS
又根据
又
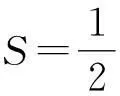
得
代入得
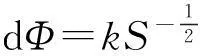
定积分式为
积分得
又当位移为a时,有
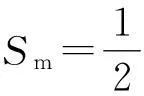
代入得
Φm=2ka
综上所述,通过以上有4种思路的讨论,揭示了磁通量但总的来说是磁场与面积积累的结果,所以处理磁感应强度及面积同时变化时,磁通量的计算问题大多使用微元累加(即积分)思想,这对学生对数学中微积分的思维能力提出了更高的要求.

