用EXCEL的“单变量求解”分析一道物理题
用EXCEL的“单变量求解”分析一道物理题
渠雷雷
(蚌埠第二中学安徽 蚌埠233000)
摘 要:针对一道单变量的物理题,应用学生已掌握的物理知识,找出各物理量之间的关系,得到含有一个变量的方程式.由于该方程用人工求解难度较大,在此采用EXCEL相关命令进行了求解和讨论.
关键词:单变量物理题EXCEL
收稿日期:(2015-05-06)
1题目
如图1所示,质量为m=1 kg的小球从平台边缘上的A点抛出,恰好垂直撞在水平面上圆心为O的半圆形轨道的B点,已知平台与水平面间的竖直高度H=1.6 m,半圆形轨道的半径R=1 m,C为半圆形轨道的最高点,OB与OC间的夹角θ=37°,g=10 m/s2,则下列说法不正确的是
A.半圆形轨道的圆心与A点的水平距离为2 m
B.小球平抛的初速度为3 m/s
C.小球到B点时重力的瞬时功率为40 W


图1
2解析
依题意,把B点速度分解,如图2所示,由几何关系可得
在竖直方向上的分位移
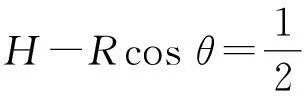

图2
以上两式联立求解可得
v0=3 m/st=0.4 s
A与O两点的水平距离为
s=v0t+Rsinθ=1.8 m
小球到B点时重力的瞬时功率
P=mgvy=40 W
以上已对A,B,C 3个选项作了分析讨论,就该题而言,此时应选A选项(因安徽省高考理综为单选).
下面重点分析D选项,按该选项的表述,是要求出小球能够越过半圆轨道的临界高度,在该高度平抛小球其轨迹应与圆相切,如图3所示.

图3
设切点为D,∠COD=α,从抛出到D点的时间设为t.
对D点速度分解,有
即
从抛出到D点,水平分位移
x=s+Rsinα=v0t
即
1.8+sinα=3t
再结合
sin2α+cos2α=1
可得
该方程人工求解非常困难.我们可以利用EXCEL的“单变量求解”命令来求解该方程.
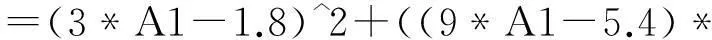

图4
(2)点击菜单选项“工具”,再选择“单变量求解”,弹出对话框后“目标单元格”设为“B1”,“目标值”设为“1”,“可变单元格”设为“A1”,如图5.

图5
(3)点击图5中“确定”后得出结果, 如图6, 即
t=0.916 811 s.

图6
把t=0.916 811 s,代入
1.8+sinα=3t
结合
sin2α+cos2α=1
得出
cosα=0.311
可得小球离地高度


可见D选项也是错误的.
3思考


