康普顿效应及其弹性碰撞恢复系数的推证
康普顿效应及其弹性碰撞恢复系数的推证
姜付锦
(武汉市黄陂一中湖北 武汉430300)
摘 要:该文通过对宏观低速的二维弹性碰撞的分析,发现其恢复系数为1;再用恢复系数对康普顿效应进行了研究,证明了(微观高速粒子弹性碰撞的典型事例)其恢复系数也为1.
关键词:康普顿效应狭义相对论弹性碰撞恢复系数
收稿日期:(2015-05-05)
1康普顿效应[1]
1921~1923年,美国物理学家康普顿在研究石墨对X射线散射时,发现散射的X射线中,除了与入射波长λ0相同的成分外,还有波长大于λ0的成分,这个现象称为康普顿效应.康普顿用爱因斯坦1905年提出的光量子概念,并引入狭义相对论.成功地解释了这种效应.他的基本思想是:X射线的光子不仅具有能量,也像其他粒子那样具有动量,X射线的光子与晶体中电子碰撞时要遵守能量守恒定律和动量守恒定律,而且还要考虑狭义相对论效应即电子质量的相对性和质能方程,求解这些方程得出的散射光波长的变化值Δλ与实验符合得很好.康普顿效应的发现,对20世纪初物理学的革命(量子论与相对论的建立)起到重大的推动作用.康普顿效应具体计算如下:
动量为p=mv,动能为E=(m-me)c2,光子与电子发生弹性碰撞,则
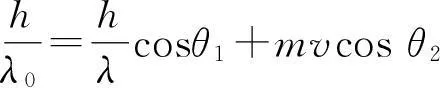
(1)

(2)
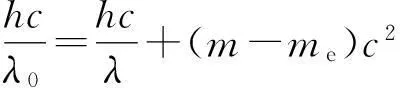
(3)

图1 康普顿效应
联立式(1)、(2)、(3)可求得
X散射光波长的变化值Δλ与实验符合得很好,由此可见爱因斯坦的光量子理论和狭义相对论的正确性.
2恢复系数[2]
牛顿在《自然哲学的数学原理》一书中首次提出恢复系数,恢复系数e由两球材料的弹性决定,其表达式为
式中v10,v20是两个物体碰撞前的速度,v1,v2是碰撞后的速度.若e=1则是弹性碰撞;若e<1则非弹性碰撞,这个公式不仅适用于一维碰撞也适用于二维碰撞[3,4].如图2所示,在光滑的水平面上,质量为m1的小球以速度v10与质量为m2速度为v20小球发生二维弹性碰撞,碰撞后两球的速度分别为v1,v2,速度方向分别与水平方向成θ1,θ2,则
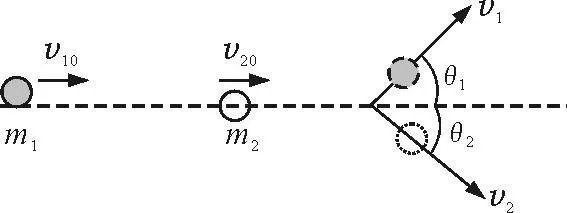
图2 两个小球的二维碰撞
m1v10+m2v20=m1v1cosθ1+m2v2cosθ2
(4)
0=m1v1sinθ1-m2v2sinθ2
(5)
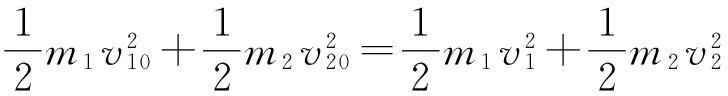
(6)
由余弦定理可知
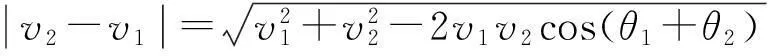
(7)
将式(4)平方与式(5)平方相加得
(m1v10+m2v20)2=
(m1v1)2+(m2v2)2+2m1m2v1v2cos(θ1+θ2)
(8)
将式(8)代入式(7)得

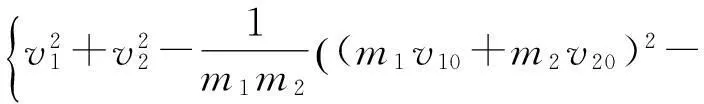

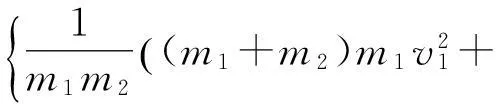
(9)
将式(6)两边同乘以2(m1+m2)得
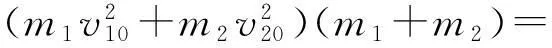
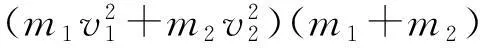
(10)
将式(10)代入式(9)得

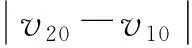
故宏观低速二维弹性碰撞中的恢复系数
3狭义相对论中相对速度[5]
由洛伦兹变换公式可以推导出相对论中的速度变换公式,设
(11)
为物体相对于坐标系∑的速度.设惯性系∑′相对于∑系沿x轴方向以速度v运动,在∑′系中物体速度分别为
(12)
由相对论时空坐标变换公式
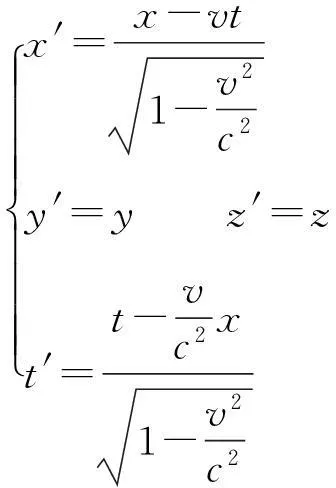
(13)
(14)
将式(14)代入式(12)得
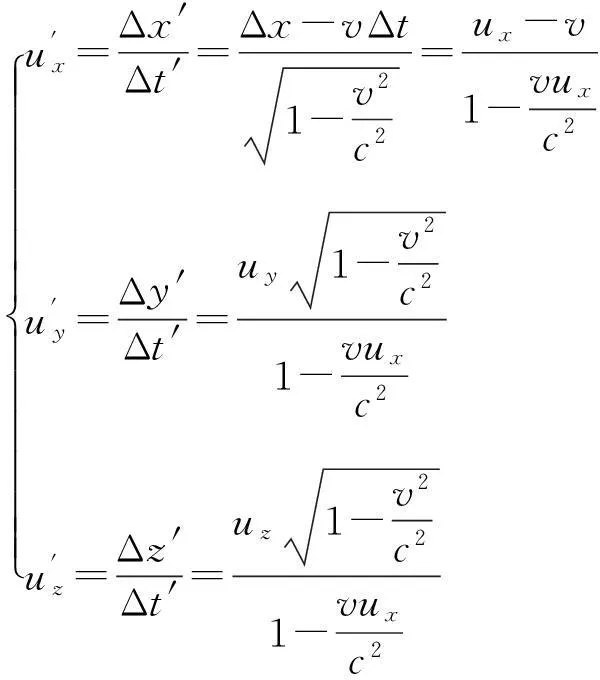
(15)
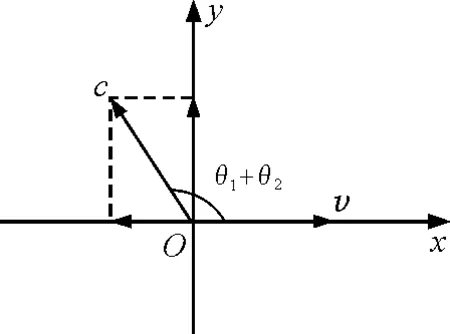
图3 光子相对电子的速度
如图3所示,X光子散射后与电子的运动方向夹角为θ1+θ2,以电子的速度v方向为x轴,与之垂直的方向为y轴建立平面直角坐标系Oxy,则光子在x轴和y轴方向上的分速度分别为
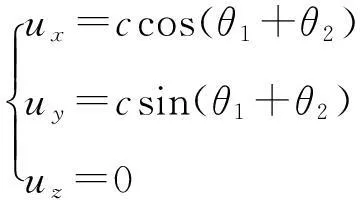
(16)
将式(16)代入式(15)得X光子相对于电子的3个分速度分别为
(17)
则光子相对电子的速度
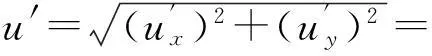

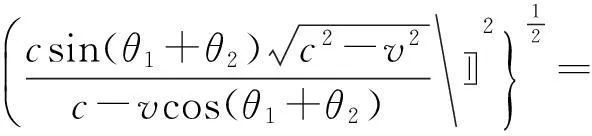

(18)
散射后光子相对于电子的速度为c,在康普顿效应中光子与电子碰撞的恢复系数也为1.
4结语
通过对宏观低速和微观高速粒子弹性碰撞的分析和恢复系数的定义式可以发现它们恢复系数均为1,它和动量守恒定律一样具有普适性.
参 考 文 献
1周世勋.量子力学(第二版).北京:高考教育出版社,2009.4~5
2漆安慎,杜婵英.普通物理学教程 力学(第二版).北京:高等教育出版社,2005.139~147
3张九铸.一般运动刚体恢复系数公式的适用条件.力学与实践,2010,3(32):116~117
4张九铸.平面运动刚体的恢复系数公式的推导.大学物理 2009,8(28):23~24
5郭项鸿.电动力学(第三版).北京:高等教育出版社,2008.192~208
Proving on Compton Effect and
Its Elastic Restitution Coefficient
Jiang Fujin
(Huangpi No.1 High School, Wuhan, Hubei430300)
Abstract:This essay analyzes the elastic collision at macro low speed in 2-dimension, finding the Coefficient of restitution 1.Furthermore, some researches are conducted on the Compton effect through the Coefficient of restitution, which proves that the Coefficient of restitution in the elastic collision at micro high speed in 2-dimension is also 1.
Key words:compton effect;special theory of relativity;elastic collision;coefficient of restitution

