基于Geant4模拟的康普顿散射研究

鄢雨璐， 张 乐， 刘书魁， 唐昌建， 林兴德， 幸浩洋

(四川大学物理学院， 成都 610064)

1 引 言

物质是世界的基础，然而根据实验推理，发现在宇宙当中还有我们看不到的物质，称之为暗物质. 在已知的宇宙中，暗物质约占宇宙总能量的四分之一，而可以看到的物质只占了4.9%. 虽然已经有许多证据证明暗物质存在，但是在实验中我们仍未找到暗物质，主要原因是暗物质不参与我们所知道的电磁相互作用和强相互作用. 目前已知最有可能的暗物质候选粒子模型为WIMPs，由于本底的影响，使得探测WIMPs的难度增大[1]. 因此暗物质直接探测实验通常都是在低本底的环境中进行. 然而CDEX实验发现，即便在地下2.4 km处依然有gamma信号存在[2]，gamma信号会对低能本底信号产生重要影响，而且当前暗物质探测实验探测能量阈值越来越低，这就要求我们必须充分理解本底能谱当中出现在低能区域的gamma本底构成.

直接探测暗物质实验中的低能gamma本底主要是来自于高能gamma射线的康普顿散射，因此需要研究低能康普顿散射沉积能谱. 目前已经有实验测量了低能康普顿散射能谱，如Barker[3]发现keV能区的康普顿能谱有康普顿台阶出现. 根据现有的IA理论可知，台阶的出现是由原子的束缚效应引起的[4]，但是他们的结果只观测了356 keV的gamma射线的台阶. 为了找到影响康普顿台阶的因素，我们使用Geant4进行了模拟实验. Geant4软件广泛应用于高能物理领域，但是也可以实现一些低能物理过程，比如低能康普顿散射. 该软件使用IA理论实现对原子束缚效应的模拟. 因此我们可以通过Geant4软件来重现康普顿台阶，并研究康普顿台阶与初始光子能量的关系，以及用Kahane计算的散射函数替换软件中的散射函数，研究了不同散射函数对相邻台阶高度的影响.

本文通过对不同能量入射光子产生的康普顿台阶进行分析，得出康普顿台阶与入射光子能量之间的依赖关系. 这有助于我们在暗物质探测本底能谱中对低能本底区域的康普顿台阶有更深的了解.

2 康普顿散射理论

康普顿散射是光子与电子之间相互作用的一种物理过程. 经典康普顿散射理论最早应用于自由电子，假设电子处于静止状态，单微分散射截面是使用Klein-Nishina公式(公式1)计算[3]：

(1)

当我们研究光子与原子中的电子之间的相互作用时，上述理论就不再适用. 这是由于原子内的电子并非自由，而是会受到原子核的影响，形成束缚状态，并且不同壳层电子的束缚能级不同. 当光子因散射损失的能量接近束缚能级时，康普顿散射能谱就会产生变化(如图1所示)，在低能区域的能谱当中有数个类似于台阶的结构出现.

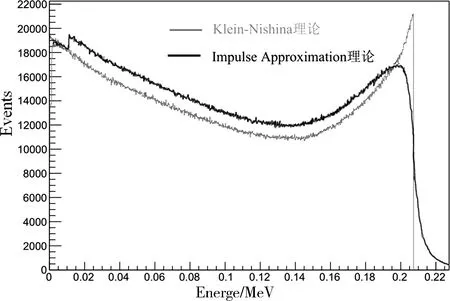
图1 考虑束缚效应的康普顿散射能谱示意图：灰色曲线为经典的康普顿散射能谱；黑色曲线为考虑束缚效应的康普顿散射能谱Fig.1 Schematic diagram of the Compton scattering spectrum considering the binding effect: the red curve is the classic Compton scattering energy spectrum; the blue curve is the Compton scattering energy spectrum considering the binding effect

为了描述这种变化产生的原因， IA理论被提出来[5-6]. 该理论将原子中的每个电子都当作独立电子，并对电子分布函数做近似计算. 计算得到的康普顿单微分截面为：

(2)

可以发现，IA理论将电子的束缚效应表达为一个因子，代表实际参与康普顿散射过程的等效电子数目，这个因子也就是散射函数. 需要注意的是，散射函数是一个与入射能量及散射角度相关的函数，在这里将其变为与动量传递相关的函数.

3 康普顿散射模拟

3.1 康普顿散射模拟设置及算法

为了探究低能康普顿散射中台阶的性质，我们使用Geant4作为主要研究工具[7]. 在软件中有3个用来处理低能康普顿物理过程的模型：Livermore模型、Penelope模型和Monash模型. 在这些模型中，原子中的电子均已考虑到原子的束缚效应. 因此模拟时我们可以发现这些模型都在高纯锗的能谱中重现了康普顿台阶结构. 锗元素的k层电子能量为11.07 keV，当光子与束缚电子相互作用使得电子壳层进行重组后，能量就会沉积. 因此对于k层电子来说，沉积能量不会少于11.07 keV. 也就是说高纯锗的康普顿能谱在11.07 keV处就会出现台阶，其他台阶出现的原因也是如此.

我们研究了Livermore模型和Monash模型. 这两个模型都使用了IA理论框架，并且都可以被用来模拟低能康普顿散射，但是依然有能量限制. 两个模型在入射光子能量为100 eV以上时才足够精确. 两个模型的不同点在于：Livermore模型是一个简单的两体模型，初始电子与反冲电子的动量均在光子平面内；而Monash模型是相对论效应下的三维两体模型，它利用特殊的相对论变换，将电子的束缚效应当作类似反康普顿散射.

模拟实验的探测器我们使用600 g高纯锗，为直径7.6 cm、高2.5 cm的圆柱体. Gamma源使用点源，垂直入射到高纯锗的圆面. Gamma能量设为239 keV、511 keV、1.46 MeV、2.62 MeV，这4种能量可以从相应的gamma放射源212Pb、22Na、40K、208Tl中得到. 每次模拟打入光子数5×108个，以保证在M层台阶尽量多的计数. 模拟中会将多次康普顿散射排除，只保留发生一次康普顿散射的事例. 另外我们将原Geant4模型中的散射函数替换为Kahane的散射函数进行了模拟，称为修正的模型.

3.2 模拟结果

在将Livermore模型和Monash模型以及修改散射函数的两个模型使用Geant4软件进行模拟后, 我们对得到的康普顿散射能谱中的每一个康普顿台阶进行线性拟合，发现每个壳层所产生的康普顿台阶的斜率与初始能量有关(如图2所示).

图2 不同模型下不同能量入射光子产生康普顿台阶的斜率:(a)K壳层康普顿台阶的斜率;(b)L壳层康普顿台阶的斜率

Fig.2 The slopes of the Compton step for incident photons with different energies under different models: (a) the slope of the Compton step of K-shell; (b) the slope of the Compton step of L-shell

通过比较，我们可以发现IA理论框架下康普顿台阶的斜率与初始能量有关. 无论是K壳层的台阶还是L壳层的台阶，都可以明显看到，随着入射光子能量的增大，康普顿台阶斜率的绝对值在误差允许范围内随之减小，直至趋近于零. 在入射能量较低的情况下，康普顿台阶斜率的绝对值受入射光子能量的影响非常明显. 随着入射光子能量的增大，康普顿台阶斜率的绝对值越来越接近于零，这种影响就变得越弱. 两个模型模拟结果的不同之处：从图2中可以看出，Monash模型得到的斜率值比Livermore模型的更大，说明Monash模型的模拟得到的康普顿台阶总是比Livermore模型更加陡峭. 这是由两个模型处理散射的方法不同引起的. 正如前文所说，Livermore模型是将康普顿散射中的所有粒子包含在一个平面中， 而Monash模型考虑的康普顿散射则是一个三维过程，存在末态电子飞出光子平面的情况. 因此两个模型的康普顿台阶斜率会受到影响，但从斜率随能量变化的趋势上来看，两个模型具有相同趋势.

4 结 论

本文通过模拟实验详细探究了入射光子能量对不同壳层的康普顿台阶倾斜程度的影响. 模拟中我们主要使用了Livermore和Monash两个康普顿散射模型[8]，并且对两个模型的散射函数进行了替换. 通过比较，发现在误差范围内可以看出康普顿台阶的倾斜程度随入射光子能量的增大而减小，直至趋近于零. 台阶受到散射结构的影响，Monash模型模拟的康普顿沉积能谱的台阶更加陡峭，斜率的绝对值比Livermore模型的大.

通过对不同入射能量的光子产生的康普顿台阶的研究，我们发现了康普顿台阶的倾斜程度随入射光子能量变化的规律，这为解析低能区域暗物质本底提供有力的依据，使得充分了解低能区域暗物质本底来源成为可能.