基于FPGA的并行DDS结构设计∗

(电子科技大学电子工程学院,四川成都611731)

0 引言

直接数字频率合成器(DDS)是Tierney等[1]于1971年提出的一种全新的频率合成技术,它相对传统技术具有频率分辨率高、频率转换时间快、易于合成复杂波形和相位连续等优点。随着技术的不断发展,它在雷达、通信、电子仪表仪器等领域具有广泛的应用。然而,人们渐渐发现这种DDS结构最大的缺点就是不能得到很高的输出频率。由奈奎斯特采样定律可知,输出频率应小于采样频率的一半,而在实际工程中输出频率只有其40%。FPGA作为一种可编程的数字集成电路,具有开发周期短、功能强、可靠性高和保密性好等优点,因此用FPGA实现DDS具有更明显的优势。本文利用FPGA实现四路并行DDS的结构,在相位累加器中结合了流水线结构,相幅转换过程中将相位分为粗调和细调两个部分,粗调仍用ROM实现,细调则利用角度旋转的方法迭代。这样,在提高输出频率、保证无杂散动态范围的同时也扩大了频谱宽度。

1 基本原理

DDS具体结构如图1所示,包括相位累加器(PA)、相幅转化器(SCMF)、数模转换器(DAC)和低通滤波器(LPF)。N位相位累加器是由加法器和寄存器组成,频率控制字K控制每次加法器步长,当其和大于2N时溢出,完成一个周期。相幅转换器最初是利用查找表(ROM)来实现,即将一个周期的正弦或者余弦函数采样2N个点存放在ROM中,并量化为W位的幅度值,然后用相位累加器作为地址控制输出。系统时钟为fclk,对应时间为1/fclk=Tclk,完成一个周期所需时间T0=Tclk×2N/K,所对应系统输出频率f0=fclk×K/2N。可以看出当K=1时,得到最小输出频率即频率分辨率fmin=fclk/2N,由此可见当N很大时可以得到非常高的频率分辨率。考虑到实际硬件条件,一般采用相位截断的方法,只取相位高M位作为ROM的地址,从而减小ROM的深度。所得到的数字信号通过DAC,其类似于零阶保持电路,将数字信号转化为模拟信号。最后通过低通滤波器滤掉杂散,得到想要的波形。

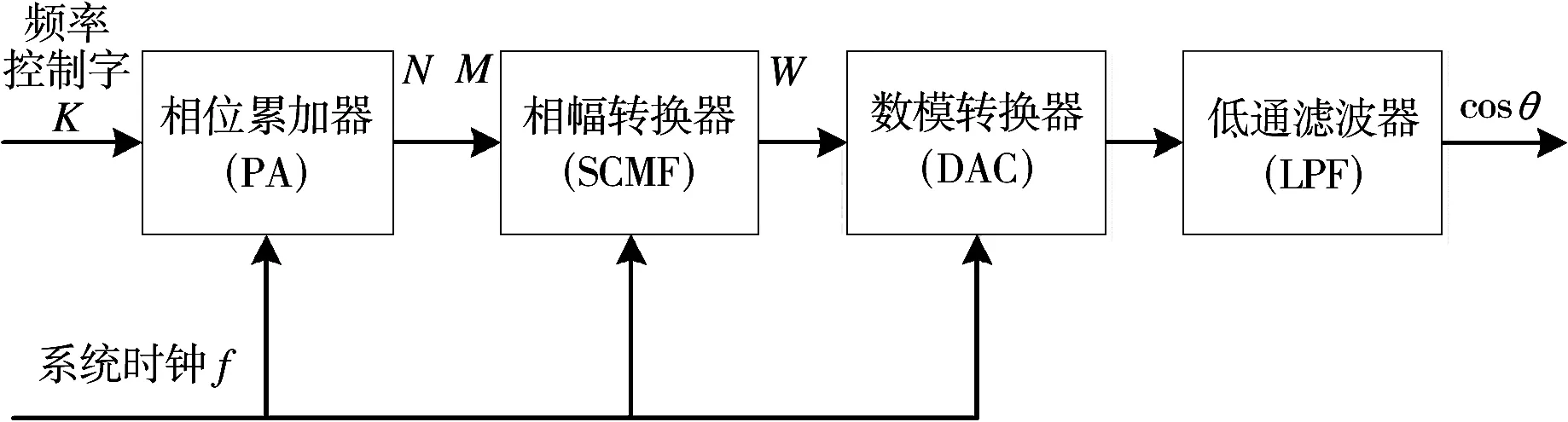
图1 传统DDS结构

2 相位累加器

运行高速系统就必须要用高速的相位累加器寻址。目前提高加法器运算速度的主要途径[2]包括:1)加快进位的产生,提高进位传递速度,缩减进位传播途径;2)降低进位的产生,提高加法器运行速度;3)根据异步电路自定时的特点,将加法器运算速度从最坏延时提高到平均延迟。已有很多文献根据这3种方法设计出高速加法器。如要用一个常规加法器实现N=32 bit的相位累加器,加法器要产生一次进位需要传播的途径太长。虽然节约了硬件,但是运行速度太慢。流水线结构是一种很常见的提高加法器速度的方法,它主要是利用缩减进位传播途径实现高速,其缺点是增加了硬件的消耗。例如将32位加法器可以分解为4个8位或者8个4位的加法器级联。为了增加加法器的吞吐量,并行的相位累加器应运而生。图2中采用4个加法器并行运算,能提高4倍的运算速度。

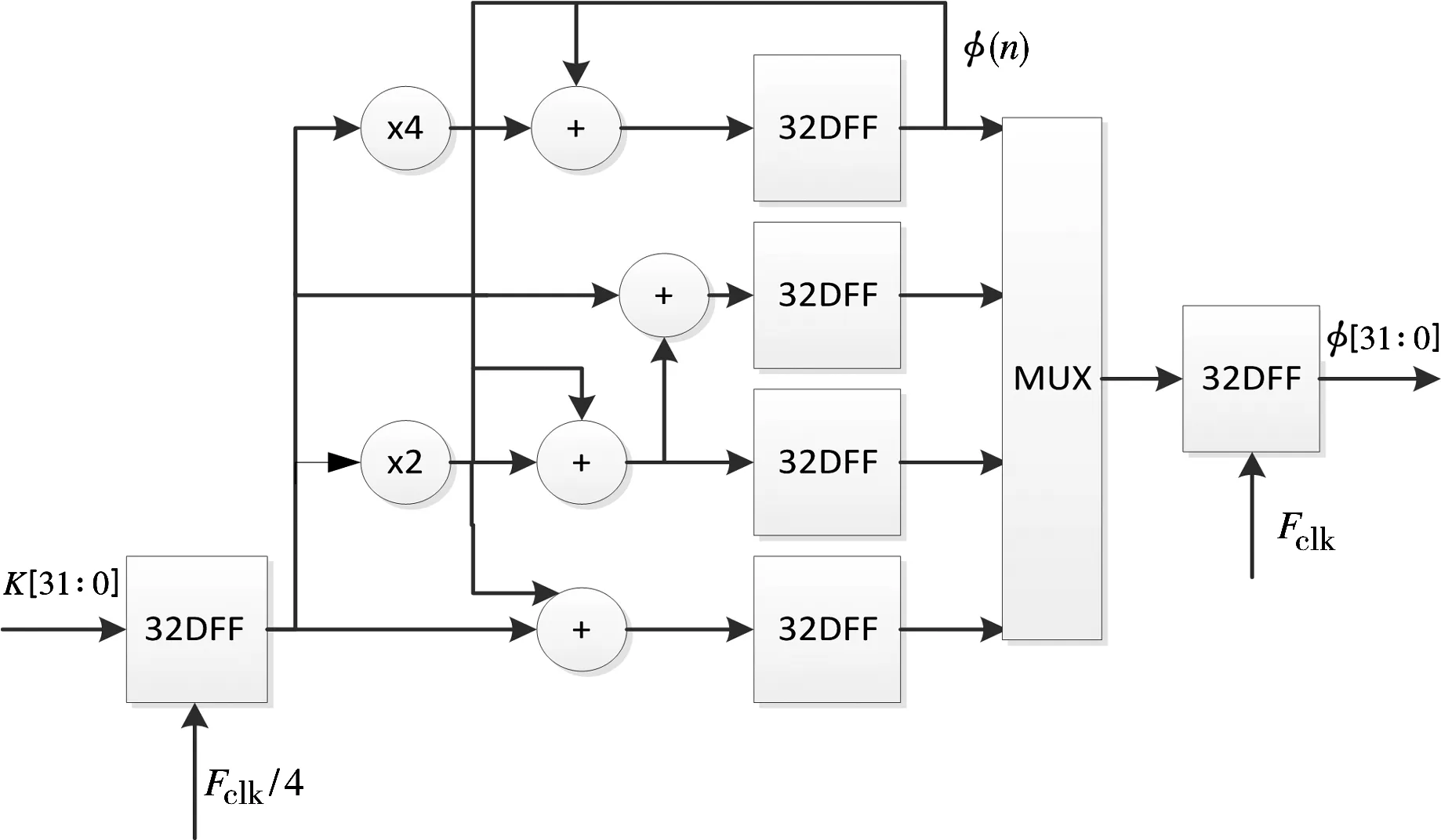
图2 四路并行相位累加器

根据上图结构,在4个时钟周期后,得到如下四路输出:

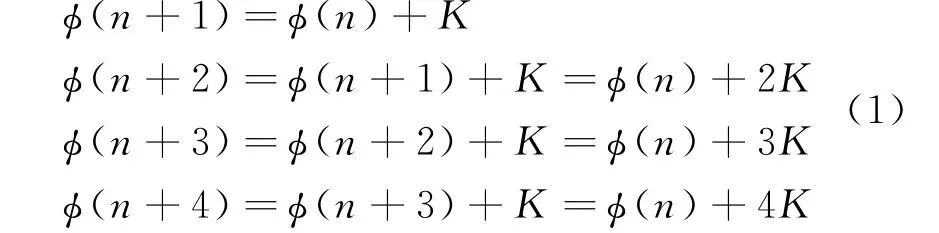
式中,ϕ(n)为第n次相位累加器输出,K为频率控制字,这里假设32位。ϕ(n+2)和ϕ(n+4)可以在加ϕ(n)之前,分别将K左移一位和左移两位得到。ϕ(n+3)就直接根据ϕ(n+2)加上K得到。每一路时钟为多路选择器工作时钟的四分之一。然而,这种结构相对于一个加法器增加了4倍的面积和功耗,其最大运行速度也仅仅为一个加法器的4倍。

为了得到更高的运行速度,可以将流水线和并行两种结构相结合得到PPA(Pipelined Parallel Accumulator)结构[3]。即将32位加法器分解为两个16位的上图结构相级联,这样相对于单单的并行加法器每一路减小了一半的进位传播途径,从而进一步提高加法器速度。具体结构如图3所示,频率控制字K低16位在第一级计算得到四路相位的低16位,并将每一路产生的进位传递给对应的高16位。频率控制字K高16位在第二级相对于第一级延迟一个周期后,四路同时运算得到四路相位的高16位。最后将高低位合并得到四路32位的相位,每一路相位值之间相差一个相位值K,从而为后面并行的DDS提供了相位偏移。

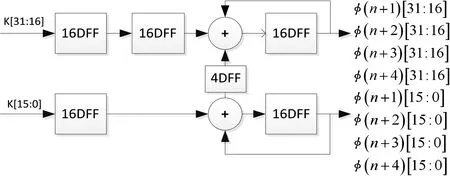
图3 PPA结构

3 相幅转换结构

传统DDS结构中ROM对运行速度和芯片功耗有很大的影响,所以在输出频谱没有较大影响的情况下应尽量减小ROM的容量。近几十年人们提出很多方法,最常见的方法是利用正弦函数的对称性,只将四分之一的波形幅度存在ROM中,然后牺牲地址高两位来映射整个周期的波形。具体包括:

1)角度分解,将相位分解为粗相位和细相位。如将相位A分为高相位C和低相位F两部分:

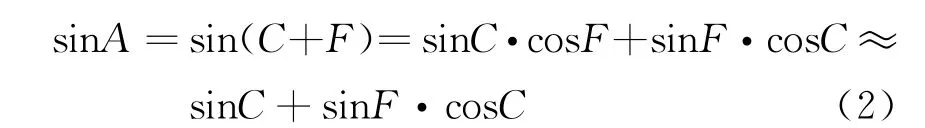
然后将两项分别放入两个RO M中,即用粗调和细调两个小ROM来代替原来的一个大容量ROM。

2)角度转换,最常见的方法就是应用CORDIC算法,如采用ROM与CORDIC相结合的方法[4]。

4)多项式近似,其中包括一阶和高阶近似,如泰勒公式展开。

本文相幅转换将相位分为粗调和细调两个部分,粗调部分仍然采用ROM的方式实现,细调部分应用类似于CORDIC算法的角度旋转结构[5]。

3.1 角度旋转算法

根据正交信号的性质可知,正弦函数在[0,π/4]的幅度值等于余弦函数在[π/4,π/2]的幅度值。因此,只需要存储第一卦限θ=[0,π/4]的幅度值,即八分之一个周期。然后利用截断后相位高三位将其映射到其他几个卦限,得到一个周期波形,具体实现如表1所示。表中地址取反,是当MSB[3]为1时,ROM地址取其反码。表中负数是根据映射规则在八分之一周期的幅度值前加上符号位。

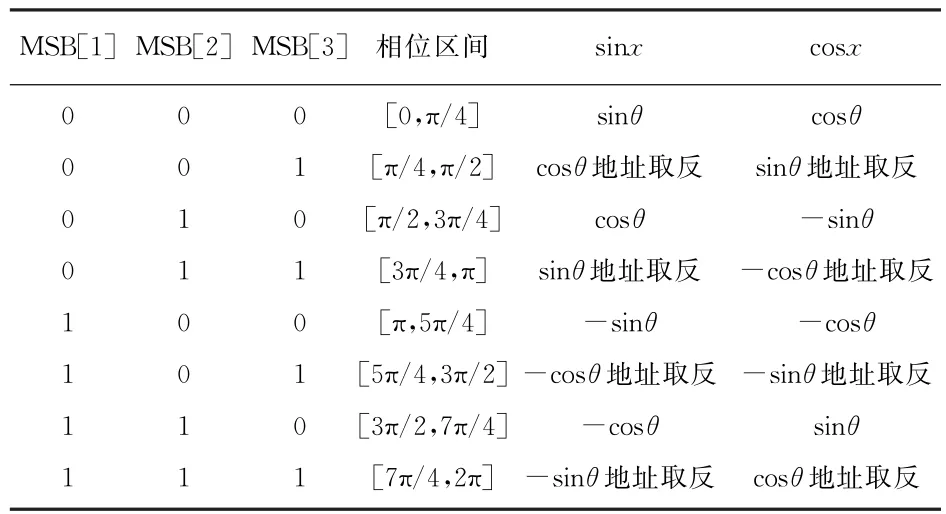
表1 卦限映射关系

在第一卦限中所有角度的弧度值是小于1的,也就都是大于零的小数。用二进制表示为θ=对b进行重新编码:

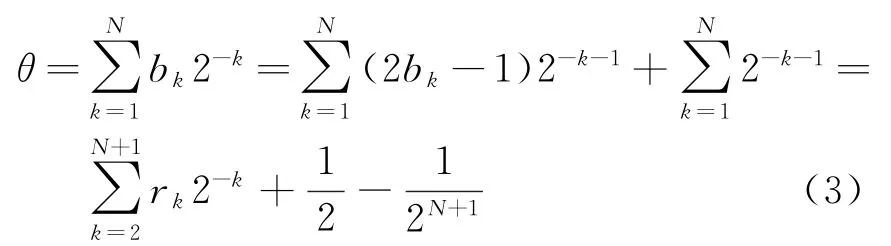
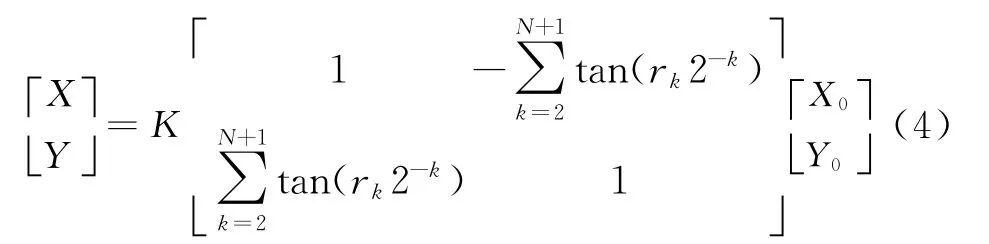
式中,X0=cosθ0,Y0=sinθ0,是一个常数。由于CORDIC算法中,第i次旋转角度满足αi=arctan2-i,通过判断旋转方向,移位相加得出结果。这里旋转角度不同于CORDIC算法,因此不能简单地通过移位相加实现。根据正切函数的泰勒公式展开式对于N位相位当k≥N/3时这里假设k=M+1满足条件,也就是粗细相位分界位在M位,M+1位为低相位的MSB。此时,式(3)可以改写为

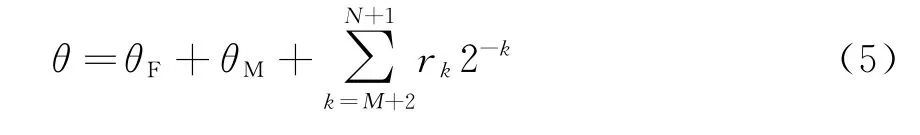
式中,XM=cos(θF+θM),YM=sin(θF+θM),同样K为常数。此时,也可以同CORDIC算法一样移位相加得到幅度。

3.2 细调部分二进制重新编码

在式(6)中,求和项相当于一个有符号数的二进制数。可以把r k重新编码成二进制补码数:t k={0,1}

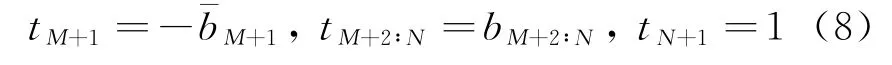
将低相位重新编码后,变成有符号的数。因此在后面的运算中应作为有符号数处理,同时相位MSB[3]控制其是否取反码。将K乘以XM,YM一起存进ROM中。式(6)可改写为

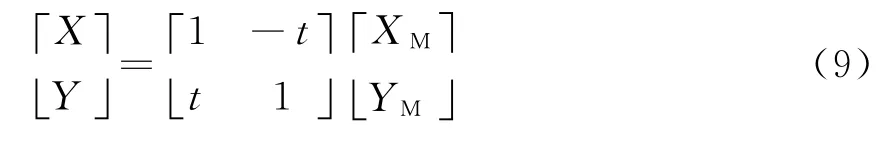
3.3 粗调部分

由于相位累加器输出相位局限于[0,π/4]内,对于32位的相位控制字K而言,0和π/4分别相当于0和4294967295,所以粗细相位都应乘以π/4。为了避免浮点运算,这里相位没有除以232。同时由式(6)知道K是独立于t的常数,所以也可将直接乘以XM和YM存入ROM中。细相位乘以π/4在其他文献中大都采用其泰勒展开式,通过移位相加得到。本文为了减小延迟和芯片功耗,根据关系式先用XM和YM乘以π/4分别得到XR和YR,并把数值存入另外两个ROM中。由于相对于存放XM,YM的两个ROM,XR和YR量化位数更少,其ROM容量更小。具体关系由式(10)给出:

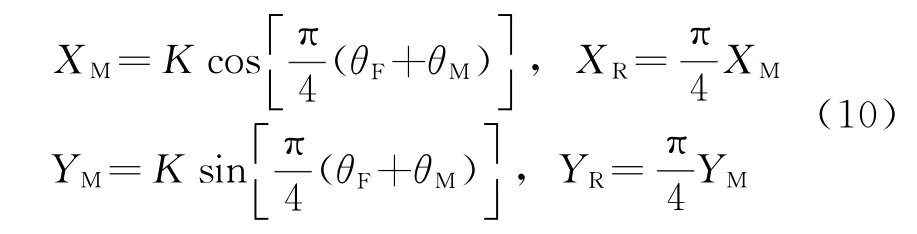
图4给出所采用的DDS结构。

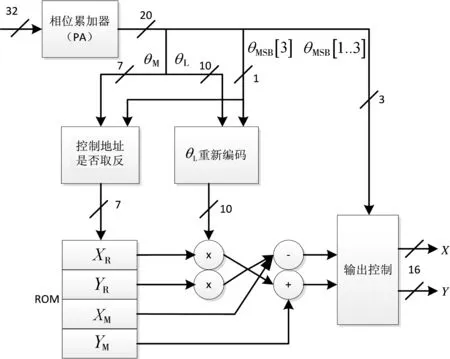
图4 ROM+CORDIC算法的DDS结构

4 总体框架与仿真

本文采用四路并行的DDS结构,相位累加器采用图3的PPA结构,每一路相幅转换采用图4结构。每一路频率控制字相当于4K,相邻两路相位控制字差为K。以单路工作时钟的4倍时钟实现并串转换,相当于四路数据相互内插。每一路输出频率为四路选择器输出为可见虽然频率控制字和工作时钟改变了,但是两个输出频率是一样的,输出频谱扩大了。具体结构如图5所示。

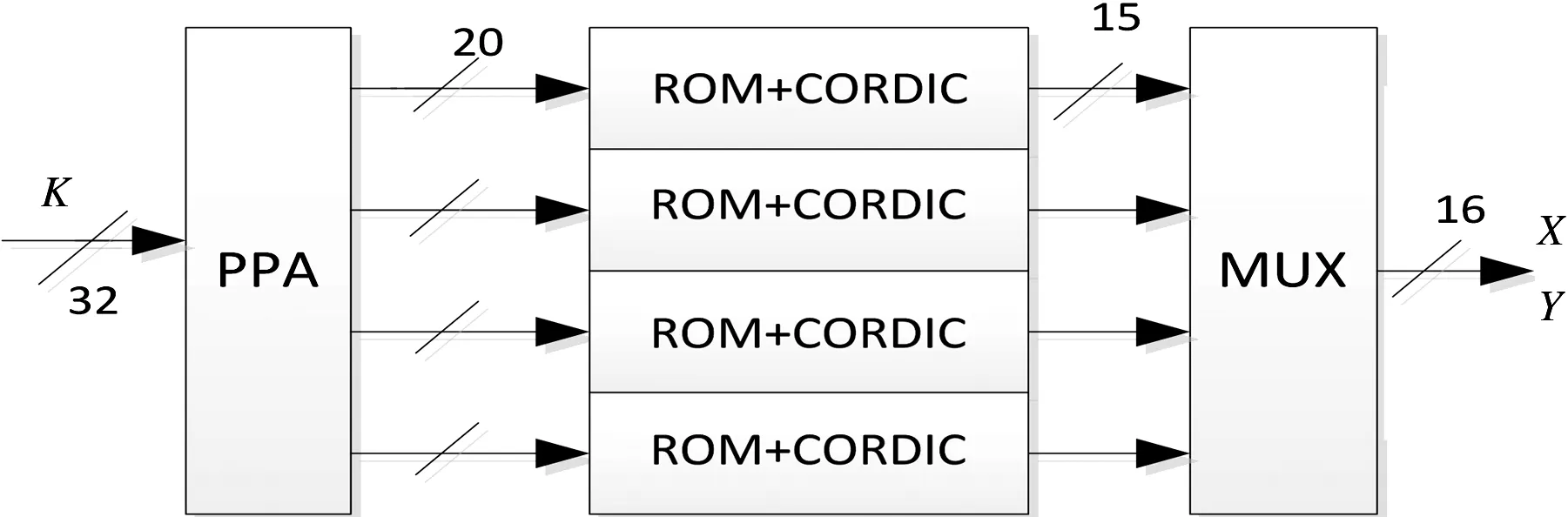
图5 四路并行DDS结构

选用Xilinx公司的XC6VLX240T芯片仿真,频率控制字K为32位,相位截断取高20位。存放XM和YM的ROM量化位数为17 bit,XR和YR量化位数为7 bit,输出信号位数为16位。XST综合后报告显示,每一路最大工作时钟可达236.351 MHz。这里系统输入时钟采用100 MHz,利用PLL倍频设置每一路DDS工作时钟200 MHz,系统总的工作时钟为400 MHz,由于FPGA将数据传给DAC,因此这里采用原语OSERDES1的ODDR模式。可知频率分辨率约为0.186 Hz。由前面的分析可知,当工作时钟为200 MHz时输出频率最大为80 MHz。图6和图7分别给出用Modelsim仿真频率为200 MHz和25 MHz的I、Q信号。

图6 频率为200 MHz的I、Q仿真信号

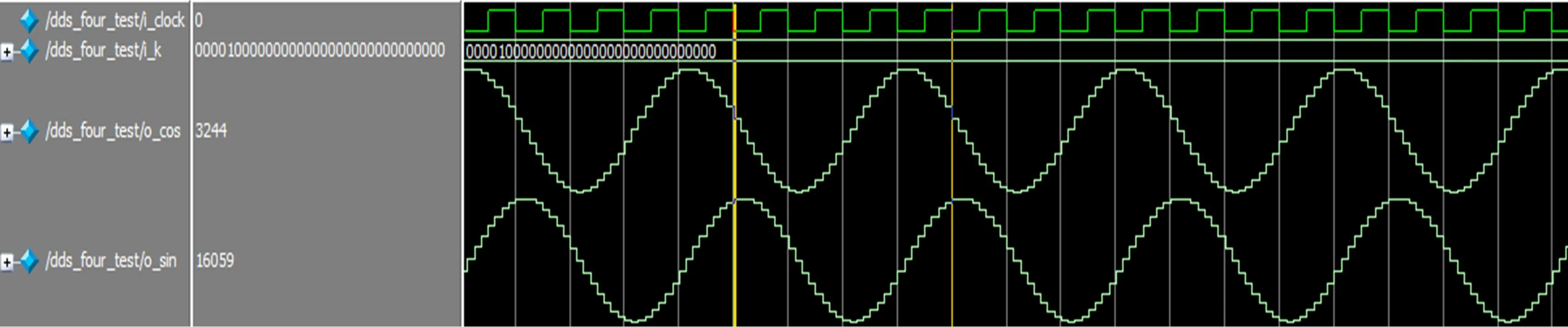
图7 频率为25 MHz的I、Q仿真信号

5 结束语

要满足高速DDS结构,相位累加器要给出高速的寻址,同时ROM不能太大。流水线和并行加法器都能提高一定的运行速度,但是又各自存在着缺点。将两种结构结合在一起,使得在速度和资源消耗方面做出了很好的平衡。减小ROM,虽然能提高一定速度和减小功耗,但是输出波形质量不能得到保证。因此,结合类似CORDIC算法迭代能得到高精度波形的特性,在提高速度的同时兼顾了波形质量。然而,它又不同于传统的CORDIC算法,每次都需要根据剩余角度判断下一次的旋转方向,从而影响运行速度。传统结构中对于17位的相位寻址,需要ROM深度为217。而采用本文中的方法仅需27,大大减小了ROM容量,从而提高了速度和减小了功耗。20位的相位寻址使得具有约-120 dBc的无杂散动态范围。当然在实际硬件实现的电路中还会存在相位噪声等因素[6]影响波形性能。并行的DDS是通过提高采样频率,增大了输出信号的频谱,同时减小了总功耗,从而在雷达系统中具有广泛的应用。

[1]TIERNEY J,RADER C M,GOLD B.A Digital Frequency Synthesizer[J].IEEE Trans on Audio and Electroacoustics,1971,19(1):48-57.

[2]袁浩,唐建,方毅.超前进位加法器的优化设计[J].通信技术,2014,47(3):339-342.

[3]YANG B D,CHOI J H,HAN S H,et al.An 800-MHz Low-Power Direct Digital Frequency Synthesizer with an On-Chip D/A Converter[J].IEEE Journal of Solid-State Circuits,2004,39(5):761-774.

[4]MADISETTI A,KWENTUS A Y,WILLSON A N.A 100-MHz,16-b,Direct Digital Frequency Synthesizer with a 100-dBc Spurious-Free Dynamic Range[J].IEEE Journal of Solid-State Circuits,1999,34(8):1034-1043.

[5]BERGERON M,WILLSON A N.A 1-GHz Direct Digital Frequency Synthesizer in an FPGA[C]∥IEEE International Symposium on Circuits andSystems,Melbourne,Australia:IEEE,2014:329-332.

[6]王勇.直接式频率合成器相位噪声限制因素[J].雷达科学与技术,2013,11(3):,329-334.WANG Yong.Phase Noise Limiting Factors of Direct Frequency Synthesizer[J].Radar Science and Technology,2013,11(3):329-334.(in Chinese)