低空目标探测中的大气折射误差快速算法∗

张 瑜,翟艳雪,甘利萍

(1.河南师范大学物理与电子工程学院,河南新乡453007;2.河南省高等学校电磁波特征信息探测重点学科开放实验室,河南新乡453007)

0 引言

利用低空(小于1 km)和超低空飞行器对敌方突袭是现代战争中常用的一种攻击手段,它不仅可以降低被探测到的概率,而且可以大大缩短敌方测量到目标进而实施有效打击的反应时间。防御方为了对该类目标进行精确定位并实施打击,雷达必须能够实现高精度和快速探测两个主要功能。目前的雷达系统硬件精度和数据处理方法的精度都较高,提高雷达测量误差的关键是对大气折射引起的误差进行修正[1-2]。在目前的大气折射误差修正方法中,公认精度最高的是电波射线描迹方法。但是由于该方法需要进行目标高度的积分计算[3-4],使其计算时间较长,不能满足快速折射误差修正的要求。因此,在保证雷达要求精度前提下提高计算速度成为大气折射误差修正方法实际应用的关键因素之一。

目前在提高折射误差修正速度方面,祝转民等[5]提出了在线算法,其主要是将目标高度的积分算法改为累加计算。尽管这样可以提高计算速度,但是随着高精度计算所需累加次数的增大,减小的计算时间很有限。武征等[6]提出了快速算法,他们主要是利用雷达所在地的统计大气环境对折射误差进行拟合,尽管计算速度较快,但是适用范围有限,且修正精度受统计的各种条件影响较大。赵乐至等[7]提出的一种快速算法是将雷达测量出的弯曲射线先作为直线来得到目标的高度,然后在此高度上增加一系数来限定目标高度,最后再在此高度利用逼近法进行积分计算。这种方法尽管可以提高计算速度,但这种人为的系数不太适应雷达仰角的变化情况。

为了提高折射误差修正的计算速度,本文引入接近目标真实高度的“虚高”概念,利用地球等效半径计算目标的虚高,然后依据分段高度采用高精度射线描迹法来进行大气折射误差修正,这样不仅可确保修正的精度,而且也可减少积分计算时间,从而可达到高精度、快速进行折射误差修正的目的。

1 基于射线描迹的大气折射误差修正方法

1.1 大气折射率模型

提高雷达大气折射误差修正精度的关键因素之一是获得高精度的大气折射率剖面。根据我国折射率分布特征[1,3]和有关统计结果,低空目标(1 km以下)所在环境内的大气折射率符合线性规律,因此其采用的大气折射率模型为

式中,h为任意海拔高度,n为任意海拔高度h处的大气折射率,h0,n0分别为地面的海拔高度和大气折射率,g为地面与离地面1 km高度之间的大气折射率垂直梯度。

1.2 计算大气折射误差的射线描迹法与分析

目前,公认高精度的大气折射误差修正方法是电波射线描迹法。假设低空目标位置为T,雷达位置为O,地球的地心为C,OC与TC之间的夹角为φ,称为目标的地心张角。一般都将雷达实际测量(包含有折射误差)的参数称为视在参数(它为已知参数),则雷达实测量参数为视在距离Re(雷达位置O到目标T之间弯曲路径的距离)和视在仰角θ0(在雷达位置O处弯曲路径切线与平行地球切线之间的夹角)。雷达测量的真实参数是未知的,也正是需要求得的。雷达到目标的真实距离R0为O到T的直线距离,真实仰角α0为在雷达O处直线R0与平行地球切线之间的夹角,如图1所示。

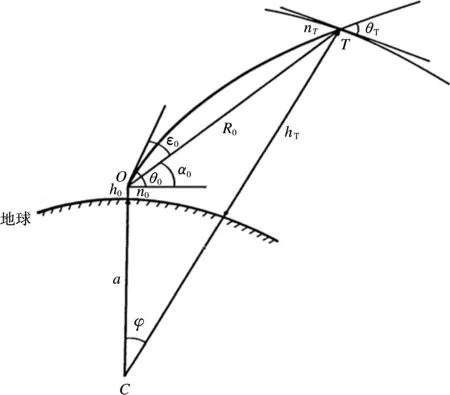
图1 雷达测量的电波折射示意图

大气折射误差修正就是根据雷达电波通过的大气环境,由雷达测量的视在参数计算得到其真实参数,此时的视在参数与真实参数之差就是大气折射误差。

根据雷达测量原理和大气球面分层的Snell定理可得雷达测得的视在距离Re[1]为

式中,a为地球平均半径,hT为低空目标的离地高度。

目标地心张角φ为

根据图1中的几何关系可得到雷达测量的真实仰角α0和真实距离R0为

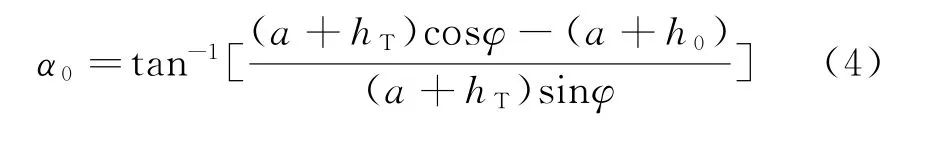
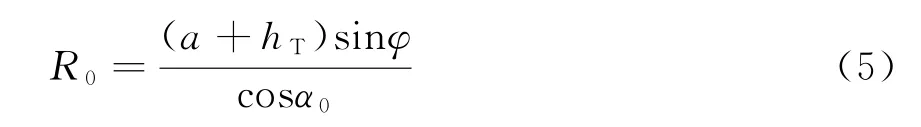
则大气折射引起的仰角误差ε和距离误差ΔR为

在进行大气折射误差计算中,大气的折射率可由式(1)得到,除了式(2)和式(3)是积分计算外,其他都是代数计算,占用计算时间很少。式(3)只有一次积分计算,占用的计算时间也较小。式(2)的作用是根据雷达测量到的视在距离Re得到目标的精确高度hT,实际上是求积分上限(目标高度),它的精度决定了大气折射误差修正的精度。由于式(2)中的被积函数复杂,只有采用逐次逼近法求得目标精确高度hT[8-9],这就需要进行多次积分运算,因此需要的计算时间最多。也可以说,利用射线描迹法进行折射误差计算时,最费时间的是目标高度hT的计算。为了提高大气折射误差修正的速度,主要应寻找使得式(2)实现快速计算的方法。

2 利用虚高计算大气折射误差的方法

复杂的被积函数使得采用式(2)进行积分计算时,常从雷达天线中心h0开始假设一个目标高度进行逐步积分计算。要得到精确的目标高度,需要采用变步长方法进行多次积分计算[1,9]。假设目标高度越接近目标的真实高度hT,需要的积分次数越少,其完成整个积分计算需要的时间就越小。为此这里引入低空目标虚高hv的概念,定义目标虚高hv为很接近目标真实高度hT的近似高度。在进行式 (2)计算时,从h0到虚高hv可以利用一次积分完成,从虚高hv到目标真实高度hT之间采用变步长的逼近法进行积分计算,这样可大大减小式(2)的计算时间。实现快速大气折射误差计算的关键是尽量使得虚高hv接近目标的真实高度hT。

2.1 地球等效半径计算

我们知道,电波射线弯曲是相对地球半径而言,如果采用等效地球半径,就可以将电波弯曲射线视为等效地球半径下的直线,用该直线就可以较精确地计算出目标的高度[10]。

以地心为原点的球坐标系中,电波在球面分层大气中传播时的Snell定理为

式中,h,n,θ分别为电波射线上任意点的海拔高度、大气折射率和电波射线仰角,h0,n0,θ0分别为雷达天线中心处的对应参数。

如果电波经过的大气均匀分布,即大气折射率n=n0=conset,则Snell定理式(7)变成

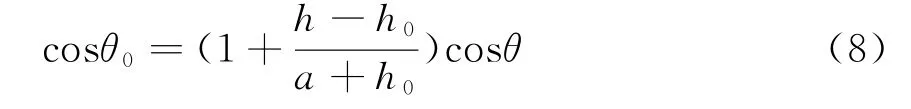
由于均匀大气中的电波不产生折射效应,因此式(8)实际上是一直线方程。

将离地面1 km内呈线性分布的低空大气折射率模型式(1)代入式(8)可得

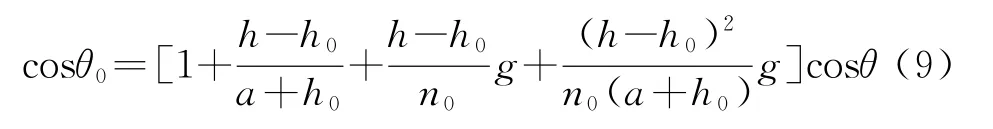
在离地面1 km高度范围内,由于h≪a,g≪1因此式(9)可简化为

则式(10)变为

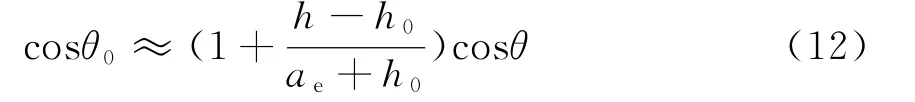
式中,ae为等效地球半径,即

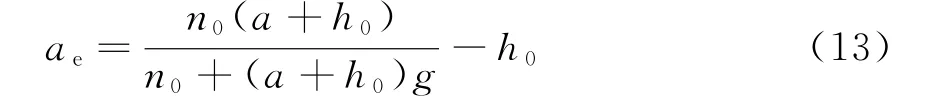
可见式(8)与式(12)在形式上完全类似,说明如果用等效地球半径ae代替真实地球半径a后,雷达电磁波射线在等效地球半径下也应是直线。用该直线进行目标虚高hv计算可使得该虚高更接近目标真实高度hT。

2.2 目标虚高的计算

由于等效地球坐标系的电波直射线与真实地球坐标系下电波弯曲射线相等,且两个地球坐标系下的仰角和高度都相等[10],因此利用几何关系可以计算出目标的虚高hv为

2.3 基于虚高的大气折射误差计算方法

在大气折射误差计算中,首先根据雷达站的大气折射率模型式(1)利用式(13)算出等效地球半径ae,再根据雷达测量出的视在距离利用式(14)计算出目标虚高hv。然后,根据式(2)首先利用一次积分计算出雷达站高度h0到目标虚高hv之间的距离,再利用变步长的逐次逼近法获得目标的精确高度hT。最后再利用式(3)～(6)可以得到大气折射误差。由于得到的虚高很接近目标的精确高度,因此在逼近时的迭代次数会大大减小,从而提高了整个折射误差计算的时间,实现了折射误差的快速修正。

3 仿真与分析

为了检验本文所述低空目标大气折射误差修正方法的计算速度,首先限定相同的精度,即设定计算目标真实高度时,得到雷达测量视在距离的误差不大于1 cm,然后采用本文方法与高精度的射线描迹法进行比较,这样就可以在相同的折射误差修正精度的条件下,进行计算速度的比较。

在仿真试验中,采用新乡地区某一天用美国AIR公司生产的高精度大气探测系统AIR-3B实测的离地面1 km的大气探空数据作为高精度射线描迹法的大气剖面。本文方法的大气剖面是先由微波折射率仪测得地面大气折射率n0=1.000 33,然后从全国低空大气折射率剖面关系数据库中得到新乡地区的大气折射率g=-49.0×10-6,1/km,最后根据式(1)获得大气剖面n。利用雷达在不同的视在仰角下测量的视在距离,采用这两种方法计算折射误差的时间如表1所示。在仿真中计算机配置:采用的电脑为Dell N4120,处理器为i5-2450M,2G内存。

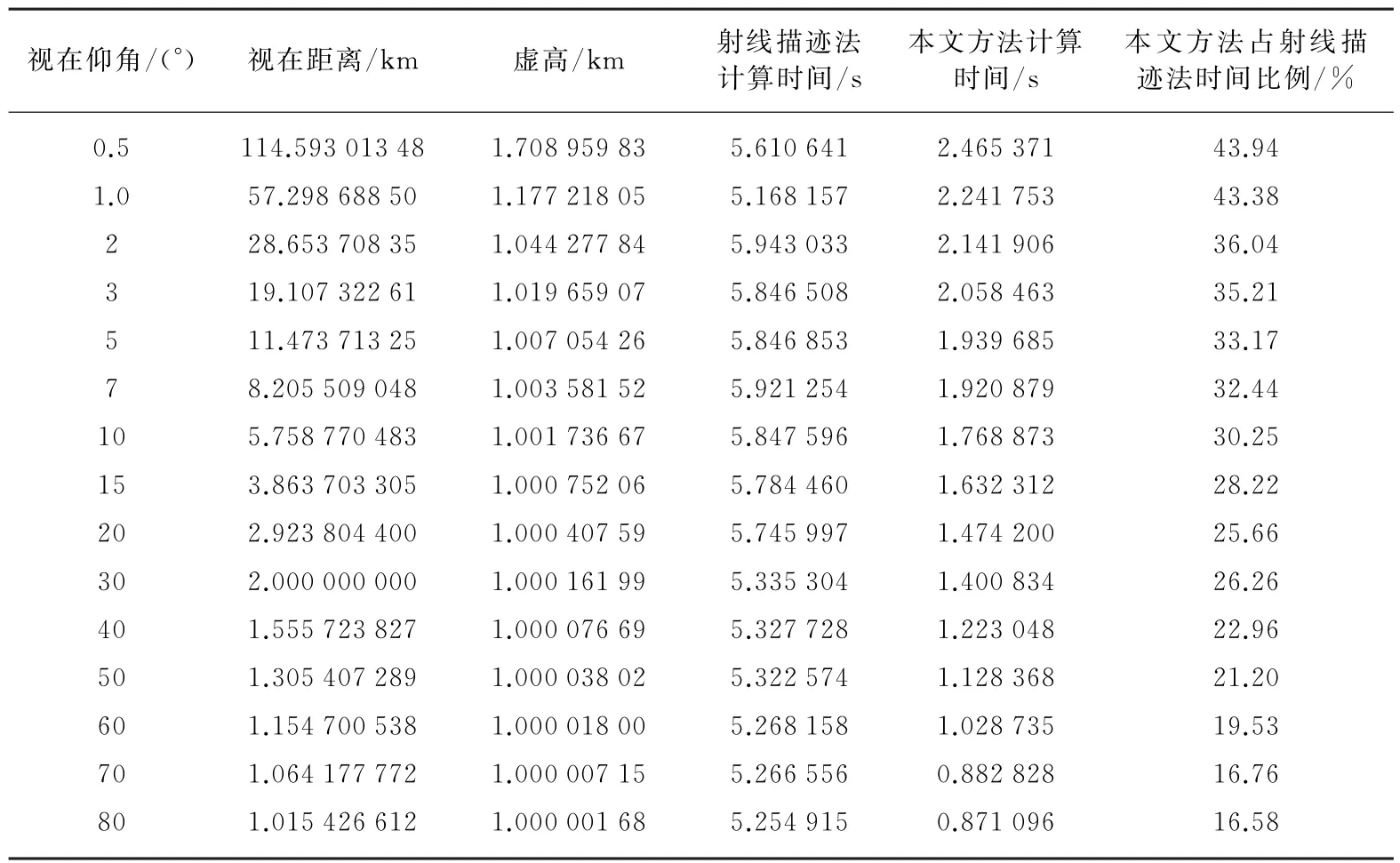
表1 两种方法计算折射误差的时间比较

从表1可见,利用高精度的射线描迹法进行折射误差计算的时间在5 s以上,而本文方法的计算时间都小于2.5 s,该需要时间小于高精度射线描迹法时间的一半以下。并且,随着雷达仰角的增大,本文方法所需要的时间逐渐减小,当雷达仰角为80°时,只占高精度射线描迹法所需时间的16.58%。说明采用本文方法进行折射误差计算时可以有效地减小处理时间,从而可实现快速折射误差修正。

4 结束语

为了进一步提高限制雷达精度的大气折射误差修正的计算速度,提出了目标虚高的概念。通过利用目标高度的虚高进行折射误差计算,不仅可以保证折射误差修正的精度,也可以提高计算速度,从而为雷达的其他处理留出较多的时间。该方法只是针对低空目标的情形,非常适用于利用低空和超低空飞行来实施突防的反舰导弹的高精度测量。下一步的研究工作一是对该方法进一步改进,使其计算速度更快,二是使其适应高空目标情形下的快速折射误差计算。

[1]张瑜.电磁波空间传播[M].西安:西安电子科技大学出版社,2007.

[2]刘波,刘宝泉,陈春晖.机载预警雷达测高精度分析[J].雷达科学与技术,2012,10(2):133-137.LIU Bo,LIU Baoquan,CHEN Chunhui.Altitude Measurement Precision Analysis of Airborne Early Warning Radar[J].Radar Science and Technology,2012,10(2):133-137.(in Chinese)

[3]JIANG Changyin,WANG Beide.Atmospheric Refraction Corrections of Radiowave Propagation for Airborne and Satellite-Borne Radars[J].Science in China:Technological Sciences,2001,44(3):280-290.

[4]张捍卫,栾军,雷伟伟.大气折射的原理性公式[J].地球物理学进展,2014,29(2):616-619.

[5]祝转民,李恒年,黄永宣,等.电波折射误差修正的精确模型与在线算法[J].系统工程与电子技术,2003,25(3):287-289,325.

[6]武征,潘佳梁,胡梦中.测量雷达对流层大气折射误差修正方法研究[J].无线电工程,2014,44(2):73-76.

[7]赵乐至,武昱,唐佩佳,等.雷达大气折射误差修正快速算法[J].四川兵工学报,2012,33(5):104-111.

[8]马东升,董宁.数值计算方法[M].3版.北京:机械工业出版社,2015.

[9]史水娥,杨豪强.电波折射误差快速修正方法[J].河南师范大学学报(自然科学版),2012,40(4):168-171.

[10]杨豪强,朱命怡,张瑜.等效地球半径的等效性与局限性研究[J].河南师范大学学报(自然科学版),2008,36(6):66-69.