具有角度稳定性的频率选择表面∗

(山东理工大学电气与电子工程学院,山东淄博255049)

0 引言

频率选择表面(FSS)是一种新型的人工电磁材料,当投射电磁波与其相互作用时会显现出带通或带阻的滤波特性,类似一种空间滤波器的功能[1-4]。通常FSS是一种二维的表面周期阵列,有贴片型(周期性排布的金属贴片)或孔径型(金属屏上周期性的开孔)两种类型。FSS可方便地通过人为调整设计参数来调整其频率特性,因此FSS的应用几乎涉及到整个电磁频谱,从可见光频谱范围直到微波频谱范围都成为研究热点[5-9]。

FSS结构为多参数设计,仅表面屏本身而言,就有谐振周期图案选形、周期图案的排列布局及衬底电介质的电性能参数等。FSS主要频率响应特性指标有谐振频率、谐频处的透过率、带宽等。同时,考虑投射到表面屏上的电磁波,投射角度和投射电磁波的偏振方式成为不可忽略的重要影响因素。FSS的实际工程应用环境中,要选用偏振稳定性好的周期单元,并且很多时候投射电磁波的投射角度涉及到大的入射范围,此时要得到优良的滤波性能指标,往往同时选用角度稳定性能较好的图形单元,才有可能得到高性能的滤波器。

常用正方形栅格排布的十字周期图案FSS,结构是对称的,因此具有正入射时的偏振稳定性,应用比较多。但是当投射电磁波的投射角度发生改变时,其谐振频率却表现出很大的漂移,频率的漂移极大地降低了FSS的性能。对此问题人们一直以来都在寻求可行的解决方法:侯新宇等通过优选图形周期图案——Y孔周期图案的方法来实现FSS对投射角度的稳定性[10];Munk等则是采用加载电介质的方式改善大角度投射时FSS的传输特性[1];贾宏燕等采用密集型周期图案排布的方法来获得大角度下FSS的稳定频率响应特性[11]。但是上述几种解决方法也同时存在一定的缺陷:Y形周期图案偏振稳定性不好[12];加载电介质又往往会增加传输损耗[13];密集型排布的周期图案会使得滤波带宽加宽影响滤波性能。

本文提出一种简单有效的新方法。以常用的正方形栅格排布的十字周期图案FSS为基础,把每个十字周期图案旋转45°叠加在原来的十字周期图案上,给出了一种优化的新型周期图案FSS设计。这种优化的FSS结构能够实现对不同投射角度中心频率的稳定性。为了进行对比分析,分别对常用的十字周期图案FSS结构和新周期图案FSS结构,利用模式匹配法进行了理论分析,同时制作了实验样件,在实验室中进行测试。

1 理论分析

采用模式匹配法分别对常用十字周期图案FSS和优化的新周期图案FSS结构进行分析。在频率选择表面两侧的自由空间,电磁场都可以用Floquet谐波模式进行展开,继而在FSS屏表面应用横向场连续的电磁边界条件,即可列出关于频率选择表面孔径周期图案的待求电场的积分方程,具体如下式所示。

式中:A r为电磁投射波的振幅值,→E b为待求的孔径电场为Floquet完备正交的谐波模式,当p和q取0值时,i为1,此时对应的模式为平面波模式,p,q不同为零值时,i≥2,此时对应其他的模式;r为不同的偏振方式,r=1,2分别代表TE和TM波;“∗”为复共轭为等效模阻抗,p和q值决定任意i阶Floquet模,并且

2 数值结果与分析

2.1 常用和改进十字周期图案FSS的设计结构

Munk在FSS的研究中指出,对于十字形的谐振周期图案,谐振现象出现在周长类比谐振波长时[1]。因此我们可以依照这个判据进行十字周期图案的参数设计,详细参数标注如图1所示。

常用正方形栅格排布的十字周期图案FSS有一个明显的特点,每个十字周期图案取向都是相同的,图2给出了常用十字周期图案FSS阵列图。在常用十字周期图案FSS的基础上,把每个十字周期图案旋转45°叠加在原来的十字周期图案上,给出一种优化的新型周期图案FSS,如图3所示。

图3 改进的十字单元FSS

常用FSS周期阵列图参数设置:阵列周期D x=D y=16 mm,臂宽w=0.5 mm,臂长L=15 mm。投射波均取45°投射角,选取频段为6～11 GHz。为了进行进一步的对比分析,图3所示的改进FSS结构,选取频段为5～9.5 GHz,其他参数设置相同。

下面分别对常用十字周期图案FSS结构和优化的FSS结构进行两个方面的对比研究:1)在一定入射角度下,不同偏振方式电磁波投射时阵列的频率响应特性;2)在一定的偏振情况下,对不同投射角度的电磁波FSS阵列中心频率的变化规律。

2.2 不同偏振方式对两种FSS频率响应特性的影响

TE,TM两种不同偏振方式的波源垂直投射时,由于周期阵列与其旋转90°后对称,传统和优化的正方形栅格十字周期图案FSS的传输特性均不受垂直入射源偏振的约束,具有较好的偏振稳定性。在大角度入射时,选取45°角入射为例,给出了两种FSS结构的频率响应曲线,如图4和图5所示。图4表明常用FSS结构在TE偏振45°角入射的电磁波投射时,中心频率为9.8 GHz,当TM偏振45°角入射的电磁波投射时,中心频率向低频漂移到了9 GHz,中心频率漂移为0.8 GHz。对于改进的FSS结构,图5表明优化的FSS结构在TE偏振45°角入射的电磁波投射时,中心频率为8.9 GHz,当偏振方式为TM时,中心频率同样向着低频方向漂移为8.5 GHz,但是漂移量与传统FSS结构相比要小,为0.4 GHz,为传统FSS结构漂移量的一半。改进的FSS结构比传统FSS具有更好的极化稳定性。

图4 传统十字单元FSS不同极化方式的频率响应

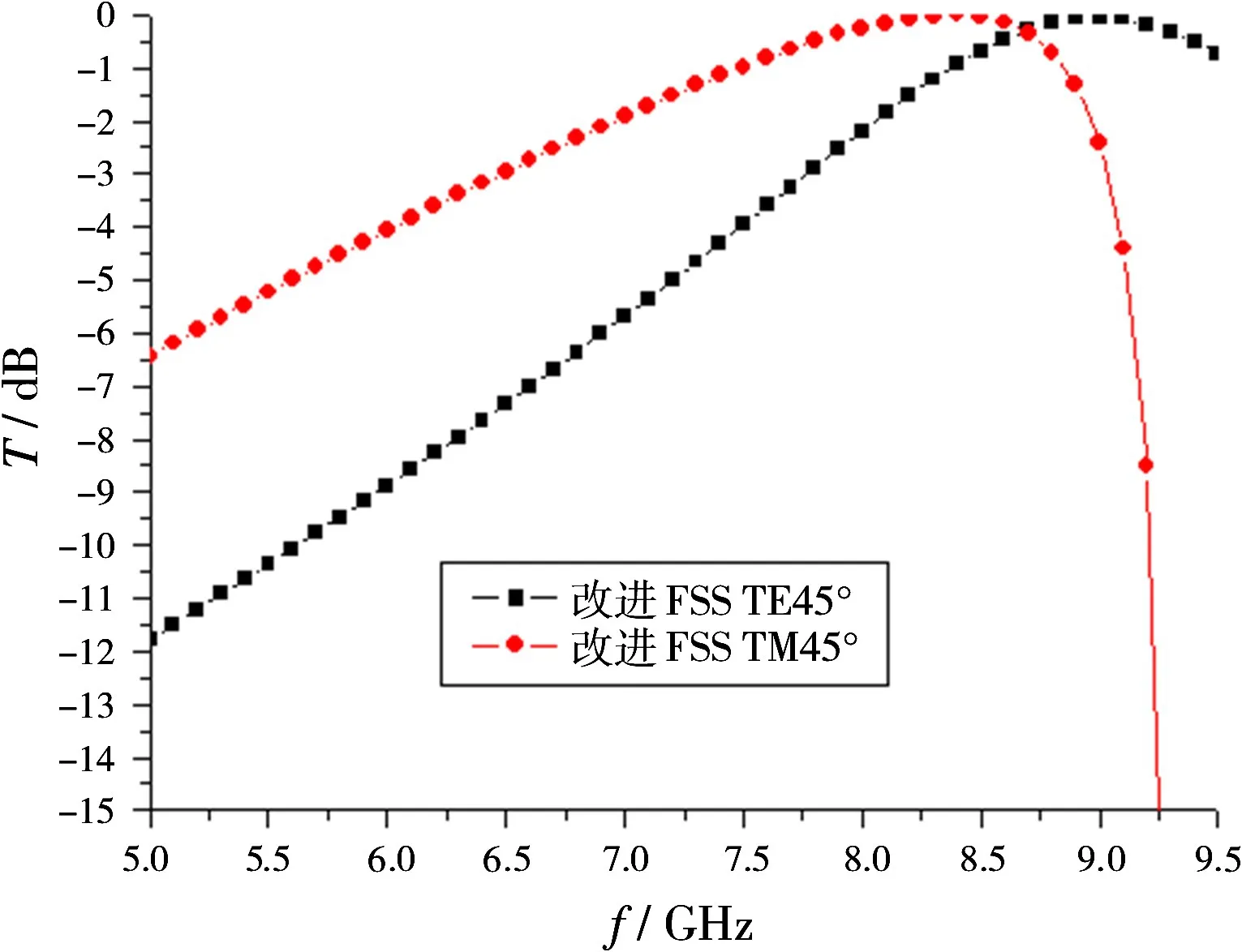
图5 改进FSS结构不同极化方式的频率响应

2.3 不同投射角度对两种FSS频率响应特性的影响

FSS工程应用中经常涉及到不同角度投射的情况,在考虑选取偏振稳定性能较好的对称单元的同时,必须考察FSS的中心频率对不同投射角度的稳定性。下面针对上述两种FSS结构,分别计算出正投射时的中心频率,然后改变投射角度,得出不同投射角度下原中心频率处的透过率系数,由中心频率处透过率的变化可以得出中心频率的角度稳定性。正投射时中心频率分别为9.5 GHz和9.2 GHz。以TE偏振方式为例,选取角度变化范围为1°到45°角度,步长为4°。计算结果如图6所示。

由图6给出的数据可以很明显地看出,对于常用十字周期图案FSS结构,投射波的投射角度由正投射逐渐变化到45°投射时,中心频率点的透过率随投射波角度的变大而降低:正投射时透过率为-0.001 7 dB,45°投射时变为-0.624 dB。中心频率点的透过率降低是由于中心频率随投射角度变化发生了漂移。这在很多涉及到大角度范围应用的情况,降低了FSS性能从而限制了FSS的应用。相比较而言,对于优化的FSS结构,投射角度由正投射逐渐变化到45°时,中心频率透过率几乎不发生改变:正投射时为-0.008 8 d B,45°投射时为-0.194 dB。

通过计算可以看出常用FSS结构的频率响应虽然能具备正入射时的偏振稳定性,但是当投射波投射角度改变时,中心频率的透过率有很大的下降;而对于改进结构的FSS具有更优的传输特性,在具有较好的偏振稳定性能的同时,能够对于不同的投射角度得到较稳定的中心频率。

3 实验测试

目前FSS的工艺制备有很多新方法[14],本设计仅对研究平面型的FSS结构,因此可采用镀膜和光刻的方法制备FSS测试样件[15],尺寸为300 mm×300 mm,此时等效认为是无限周期的FSS。在实验室中对两种实验样件进行偏振稳定性和角度稳定性两方面的实验测试,以验证理论计算结果。

投射电磁波在不同的偏振方式时,测试FSS设计屏的偏振稳定性。实际测试中,TE波与TM波的不同偏振方式的转换,可以旋转FSS表面屏90°来实现,而不需要像常规测试中调整发射设备。常用和优化的FSS结构的实验样件测试结果如图4、图5所示,测试值和理论计算值基本一致。对两种FSS结构中心频率的角度稳定性进行测试时,选定TE极化方式,转动测试件转台,使投射角度由正投射逐渐增大到45°投射,旋转角度间隔取为4°。测试值和测试照片分别如图6和图7所示,测试结果验证了理论值的正确性。

图6 两种FSS结构中心频率透过率随入射角度的变化

图7 FSS测试系统

4 结束语

投射波的投射角度一直是影响FSS传输特性的一个重要因素。本文选取正方形栅格十字周期图案FSS结构为基础进行改进,设计了由十字周期图案旋转45°叠加得到的一种新型周期图案频率选择表面。计算和测试结果均表明:常用的十字周期图案FSS具备正入射时的偏振稳定性,但是当波源的投射角改变时,FSS中心频率处传输损耗会很大,而优化的FSS结构在大角度入射时具有更好的偏振性能,且能够实现中心频率对投射角度的稳定性。它可以为很多涉及到曲面大范围角度投射的情况提供一定的设计思路,如卫星通信领域及隐身曲面雷达罩的设计。

[1]MUNK B A.Frequency Selective Surface:Theory and Design[M].New York:Wiley,2000.

[2]WU T K.Frequency Selective Surface and Grid Array[M].New York:Wiley,1995.

[3]YU Miao,XU Nianxi,GAO Jinsong.Infrared Transparent Frequency Selective Surface Based on Iterative Metallic Meshes[J].Chinese Physics B,2015,24(3):107-110.

[4]路宝,龚书喜,凌劲,等.一种新型频率选择表面及其在天线雷达散射截面减缩中的应用[J].电子与信息学报,2010,32(1):199-202.LU Bao,GONG Shuxi,LING Jin,et al.A Novel Frequency Selective Surface Structure and Its Application to RCS Reduction of Antennas[J].Journal of Electronics&Information Technology,2010,32(1):199-202.(in Chinese)

[5]刘晓春,张文武,孙世宁.频选雷达罩电性能的基本问题及解决方法[J].雷达科学与技术,2012,10(3):336-340.LIU Xiaochun,ZHANG Wenwu,SUN Shining.Elementary Problems and Solutions for Electrical Performance Design of FSS Radome[J].Radar Science and Technology,2012,10(3):336-340.(in Chinese)

[6]王新彪,李靖,张升伟.毫米波/亚毫米波临边探测仪准光技术[J].太赫兹科学与电子信息学报,2013,11(4):595-600.WANG Xinbiao,LI Jing,ZHANG Shengwei.Quasi-Optical Technology in Millimeter/Sub-Millimeter Limb Sounder[J].Journal of Terahertz Science and Electronic Information Technology,2013,11(4):595-600.(in Chinese)

[7]张建,高劲松,徐念喜.光学透明频率选择表面的设计研究[J].物理学报,2013,62(14):1-7.ZHANG Jian,GAO Jinsong,XU Nianxi.Design and Study of Optically Transparent Band-Pass Frequency Selective Surface[J].Acta Physica Sinica,2013,62(14):1-7.(in Chinese)

[8]张建,高劲松,徐念喜,等.基于混合周期栅网结构的频率选择表面设计研究[J].物理学报,2015,64(6):326-332.

[9]陈亮,陈夏萌,陈强,等.基于非谐振单元的小型化带通频率选择表面设计[J].中国舰船研究,2015,10(2):84-88.CHEN Liang,CHEN Xiameng,CHEN Qiang,et al.Design of Bandpass Miniaturized Frequency Selective Surfaces Composed of Non-Resonant Elements[J].Chinese Journal of Ship Research,2015,10(2):84-88.(in Chinese)

[10]侯新宇,张澎,卢俊,等.一种双曲率雷达罩的频率选择表面分片设计[J].弹箭与制导学报,2006,26(1):123-125.HOU Xinyu,ZHANG Peng,LU Jun,et al.A Novel Frequency Selective Surfaces Patch Design for Double Curved Radome[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(1):123-125.(in Chinese)

[11]JIA Hongyan,GAO Jinsong,FENG Xiaoguo.Closely Packed Dense Frequency Selective Surface[J].Chinese Optics Letters,2008,6(6):441-442.

[12]卢俊,张靓,孙连春.Y形和Y环形单元特性的实验对比研究[J].光学精密工程,2005,13(2):219-224.LU Jun,ZHANG Jing,SUN Lianchun.Experimental Comparison of the Characteristics of Y Element and Y Loop Element[J].Optics and Precision Engineering,2005,13(2):219-224.(in Chinese)

[13]侯新宇,万伟,佟明安,等.介质损耗对频率选择表面传输特性的影响[J].电子科学学刊,2000,22(5):871-874.

[14]高劲松.基于立体打印技术制作曲面频率选择表面[J].实验室研究与探索,2015,34(3):4-7.

[15]庞玉莲,邹应全.光刻材料的发展及应用[J].信息记录材料,2015,16(1):36-51.