卫星通信中改进型变步长LMS预失真算法∗

(解放军信息工程大学,河南郑州450002)

0 引言

卫星通信因具有波束覆盖范围广和通信距离远等特点成为无线通信系统中一种重要的通信方式。随着通信业务量的增加,频带利用率高的高阶调制被广泛地应用于卫星通信中,然而其较大的包络起伏和较高的峰均功率比对非线性极其敏感。为了提高功率利用率,卫星通信系统的高功率放大器通常工作在饱和区附近,使得信号容易产生非线性失真。对于传输信号带宽的增加,星载功率放大器也会表现出显著的记忆效应。为了保证良好的通信性能,必须解决功率放大器非线性失真的问题。

预失真技术[1-3]和非线性均衡技术[4-6]都能够解决星载功率放大器非线性失真的问题。非线性均衡技术能够有效地补偿非线性失真,减少码间串扰的影响,但不能够保证通信的频谱和功率资源的有效利用,因此可以在发射端进行预失真补偿[6]。文献[3]指出Volterra模型预失真能够很好地补偿功率放大器的非线性失真,但其抽头系数较多,随着阶数的增加,计算复杂度呈严重的非线性增长。文献[7]表明可以采用记忆多项式模型来代替Volterra模型以减少运算的复杂性,同时能够保证良好的性能。对于自适应算法,常用的主要有LMS算法和RLS算法。文献[8-9]分别运用LMS算法于Wiener模型和Volterra模型中,并分别推导了非线性信道LMS算法和滤波LMS算法,然而LMS算法收敛速度慢、稳态误差大。文献[10-11]分别简化RLS算法和基于RLS的常模算法,相比LMS算法,RLS算法和简化RLS算法具有较快的收敛速度,但计算复杂度较高。文献[12]提出了SHNLMS(Shrinkage Normalized Least Mean Squares)算法,进一步提高了NLMS算法的收敛性能。文献[13]提出了一种变步长修正LMS(Variable Step-Size Modified Least Mean Square,VSSMLMS)算法,相比LMS算法,其具有较快的收敛速度和较低的稳态误差,同时有效地解决了功率放大器非线性失真的问题,然而其收敛速度和稳态误差性能有待于进一步提高。

为了进一步优化变步长LMS算法,提高算法的收敛性能和均方误差性能,本文提出了一种IPVSSLMS预失真算法。仿真结果表明,相比于LMS算法、SHNLMS算法和VSSMLMS算法,该算法在解决功率放大器非线性失真的同时,不仅能够有效地提高了收敛速度,而且能够获得较小的稳态误差。

1 系统模型

卫星通信系统等效模型如图1所示。在发射端,发射信号分别经过调制、平方根升余弦发送滤波器(Square Root Raised Cosine Filter,SRRC)、预失真器、星载高功率放大器(High Power Amplifier,HPA)后到达信道;在接收端,接收信号先经过匹配滤波器和判决后即可得到所需信号。其中,AWGN为高斯白噪声。

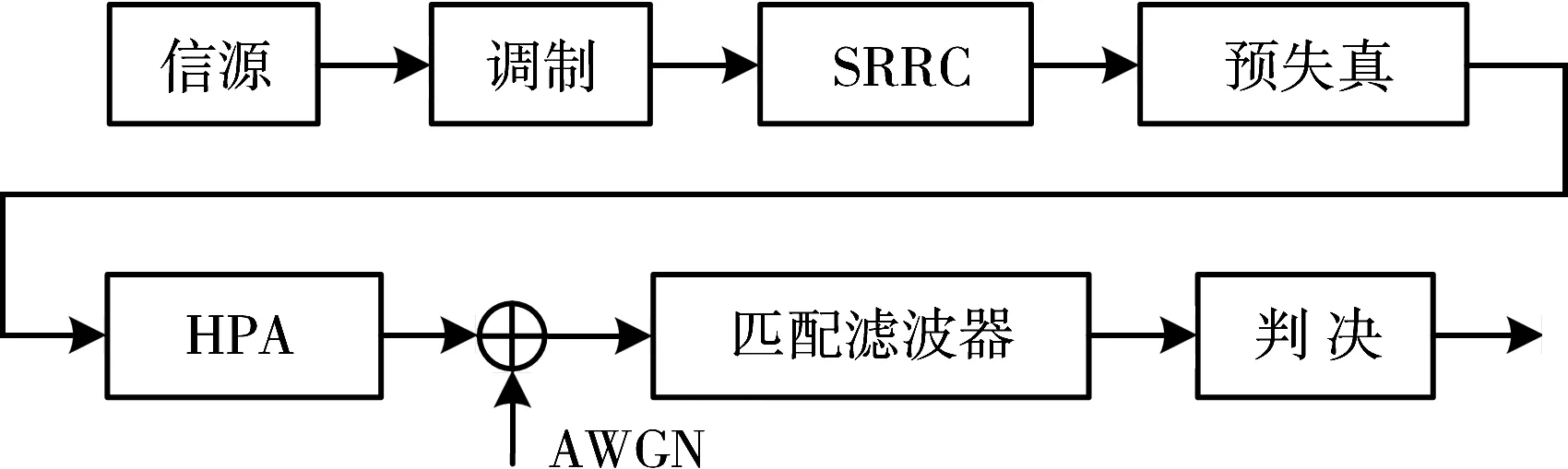
图1 卫星通信系统模型

图2给出了图1系统中预失真器工作原理,其中预失真为奇数阶记忆多项式模型[13],且多项式训练模块与预失真完全相同。HPA为Saleh模型的行波管放大器(Traveling Wave Tube Amplifier,TWTA)。多项式预失真的目的是使预失真输入信号与HPA输出信号之间满足线性关系。其中,x(n)和y(n)分别为预失真器和HPA的输入信号分别为HPA和预失真训练模块的输出信号。

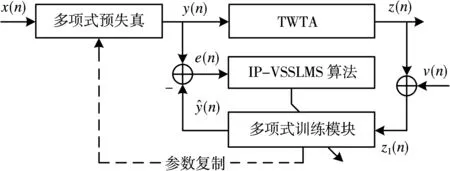
图2 间接预失真工作原理

图2中,预失真输入信号x(n)经过多项式预失真后,可得预失真的输出信号为

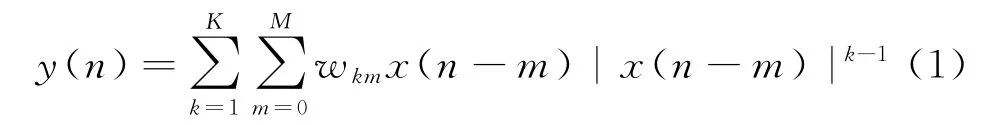
式中,K和M分别为最高阶次与记忆深度,k为奇数,w km为预失真参数。

HPA的输入信号和输出信号之间会出现幅度-幅度(AM-AM)和幅度-相位(AM-PM)效应,使得HPA的输入信号y(n)和输出信号z(n)之间呈非线性特性。即满足

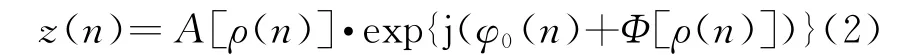
式(2)中,HPA的输出信号z(n)再分别经过噪声和预失真训练模块后有

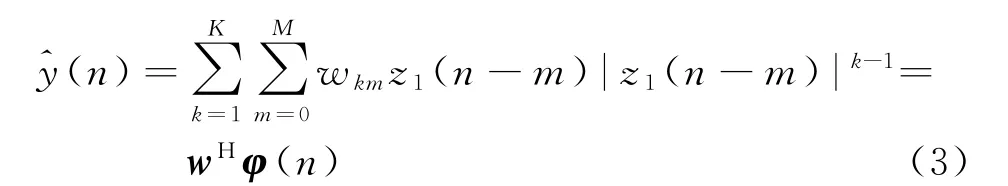
式中,w=[w10,w11,…,w1M,w30,w31,…,w KM]T,φ(n)=[z1(n),z1(n-1),…,z1(n-M)|z1(n-M)|K-1]T,z1(n)=z(n)+v(n),v(n)为加性高斯白噪声。

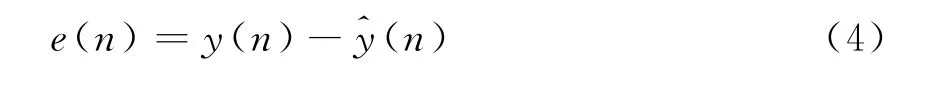
2 LMS算法、VSSMLMS算法和IP-VSSLMS算法

2.1 LMS算法和VSSMLMS算法

LMS算法因具有计算复杂性低和易于实现的特点而得到广泛应用,其权系数迭代公式为

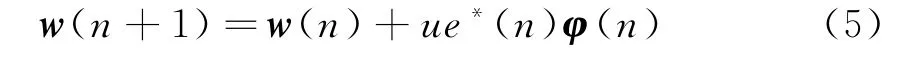
式中,w(n)为多项式权系数矢量,e(n)和φ(n)分别满足式(3)和式(4),u为收敛步长因子且满足

式中,λmax为输入信号φ(n)自相关矩阵特征值中的最大值。由式(5)和式(6)可知,算法的收敛速度和稳定性等都与步长因子u有关,因此,提高算法的性能必须从改变LMS算法的步长因子出发。

为了有效地提高LMS算法的收敛速度和稳态误差等性能,文献[13]提出了VSSMLMS算法,其权系数迭代公式为

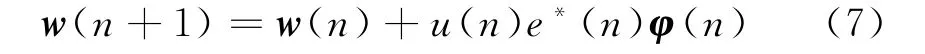
式中,u(n)为变步参数,且满足

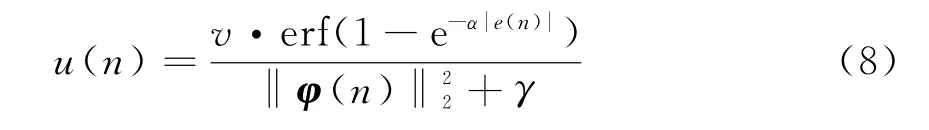
2.2 IP-VSSLMS算法

为了进一步提高LMS算法的收敛性能,引入输入信号矢量能量的期望值和误差信号能量的期望值于LMS算法中,同时利用VSSM LMS算法的优点,得到了一种IP-VSSLMS算法。IP-VSSLMS算法的变步长收敛因子为

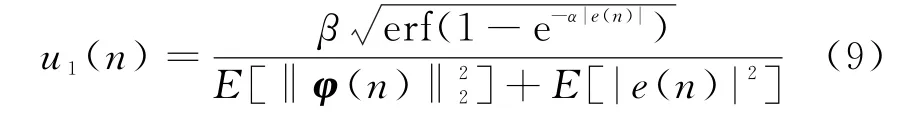
式中,α和β为控制收敛速度的调整参数。

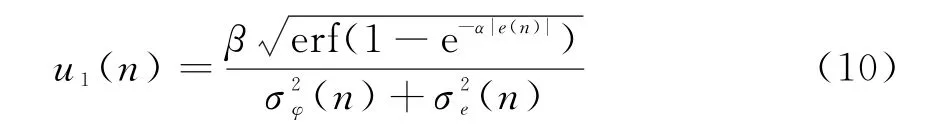
由式(10)可知,IP-VSSLMS算法的权系数迭代公式为

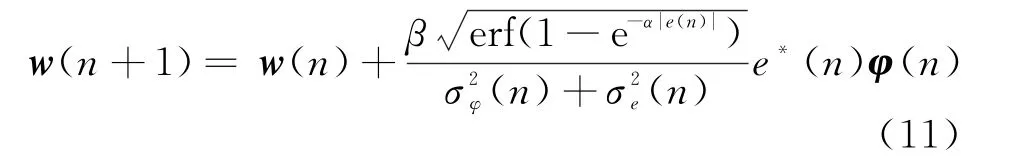
由LMS算法和NLMS算法可知,步长因子满足0＜u＜2/λmax,因而可知IP-VSSLMS算法中满足

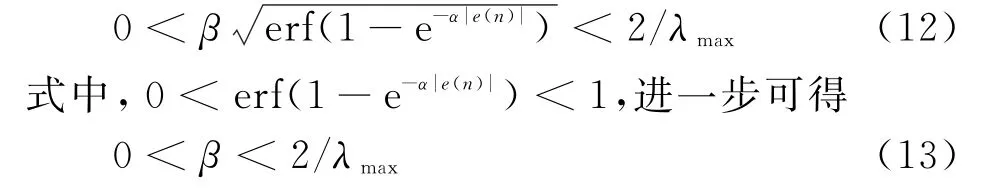
相比VSSMLMS算法和LMS算法,IP-VSSLMS算法用输入信号矢量能量平均值和误差信号的能量信号平均值,不仅能够从整体角度提高收敛性能,而且有益于降低算法的稳态误差。

3 性能分析

3.1 稳定性分析

若在每一次迭代过程中,多项式滤波器处于理想最佳时权系数迭代矢量为wopt,令v0(n)=woptw(n),则可得

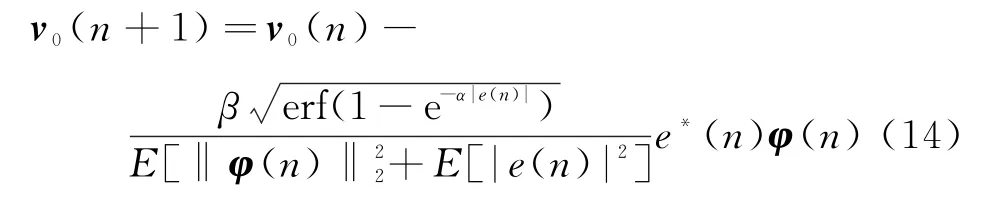
那么,v0(n)的均方误差可定义为

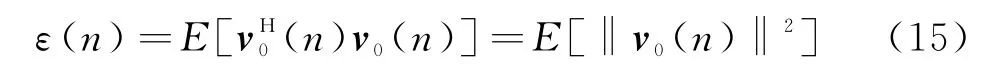
为了使算法处于稳定状态,则必须使ε(n+1)-ε(n)＜0,综合式(14)和式(15)可知

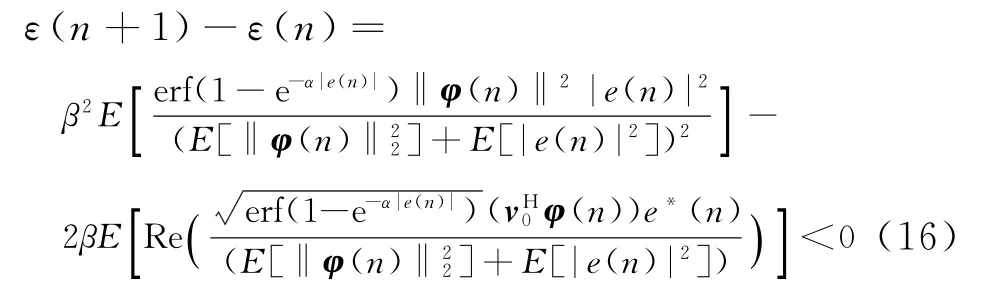
将式(16)化简整理并综合式(13)可知,算法稳定性时β为

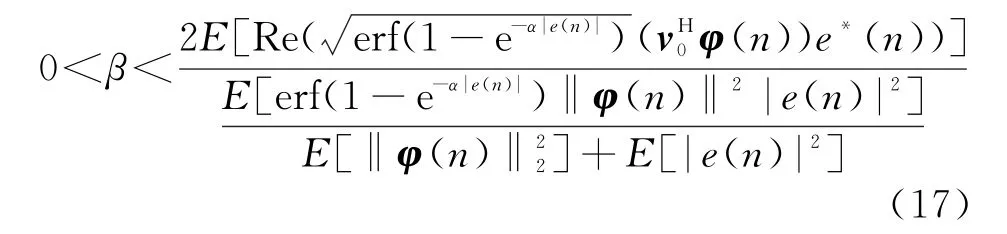
3.2 收敛性分析

为了便于研究,再次使用式(14)可得

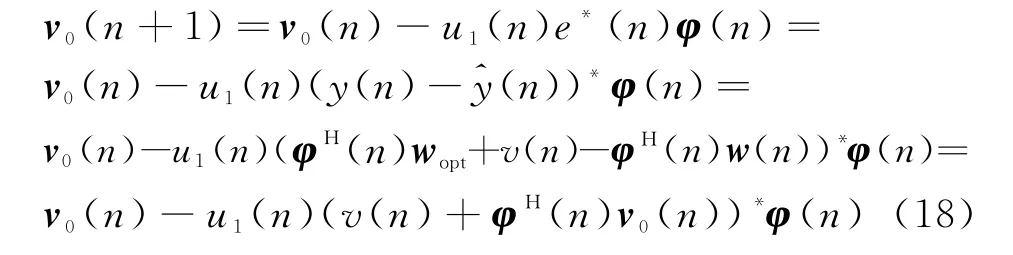
式中,v(n)为系统噪声。

于是,将式(18)进行求期望处理可知

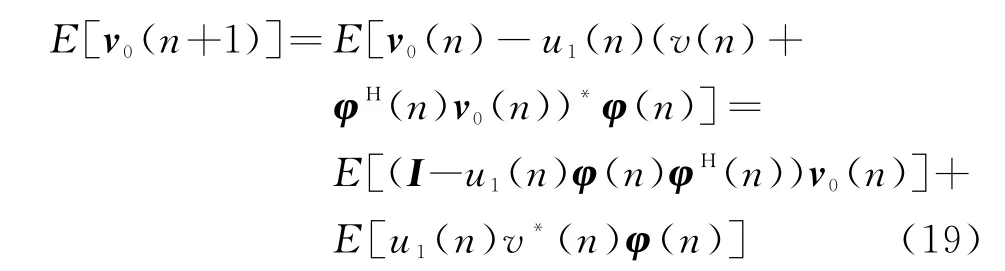
假设u1(n)是与时间无关的定值,并且φ(n)与v0(n)、v(n)之间是统计独立的,则由式(19)可得E[v0(n+1)]=(I-u1(n)R)E[v0(n)]=

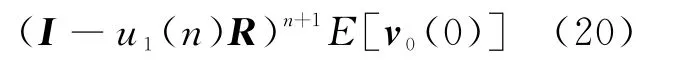
如果将式(20)左乘QH,其中Q为使R相似变换为对角化的酉矩阵,则可以得到

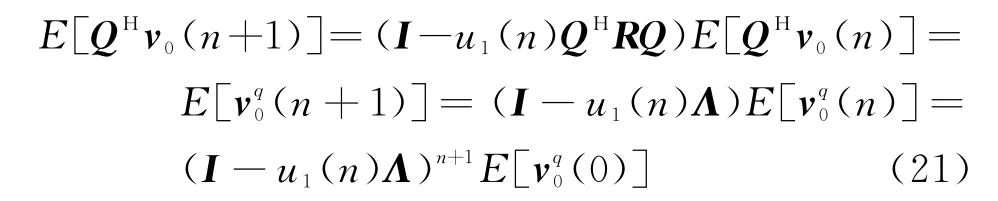
综合式(13)和式(17)可知

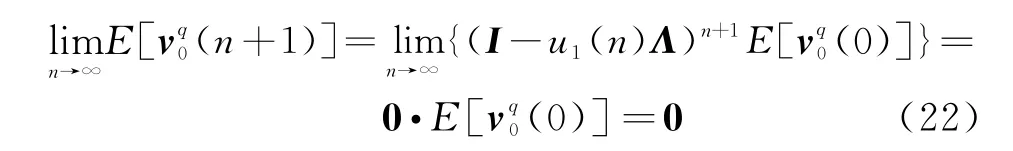
因此,当n→∞时,权系数矢量w(n)能够收敛到最佳系数矢量wopt。

4 仿真结果

仿真实验中,调制方式为APSK调制,并参照DVB标准选取内外半径比为2.732的4+12-APSK调制,发送滤波器和匹配滤波器的过采样因子和滚降系数分别为8和0.35,多项式预失真器的最高阶数K=3,记忆深度M=10。算法的初始化参数为:LMS算法中u=0.1;SHNLMS算法[12]中λ=0.99,L=1;VSSMLMS算法[13]中v=1.2,α=50;IP-VSSLMS算法中β分别选取β=1.2和β=2.1,α=50。

为了比较各算法之间的性能,图3给出了各算法归一化均方误差的仿真结果。由图3(a)可知,VSSMLMS算法经过3 000次迭代后收敛到-34 dB,而IP-VSSLMS算法在β=1.2和β=2.1时分别收敛到-37 d B和-38 d B;相比而言,IPVSSLMS算法的归一化均方误差性能明显优于VSSMLMS算法,并且β取值越大算法性能越好。由图3(b)可知,LMS算法经过1 000次迭代后收敛到-25 d B,SHLMS算法经过400次后收敛到-27 d B,VSSMLMS算法经过250次后收敛到-32 d B并最终收敛到-34 d B,IP-VSSLMS算法在β=2.1时经过100次后收敛到-36 d B并最终收敛到-38 d B。由此可知,相比LMS算法、SHNLMS算法和VSSMLMS算法,IP-VSSLMS算法具有较快的收敛速度和较小的归一化均方误差。

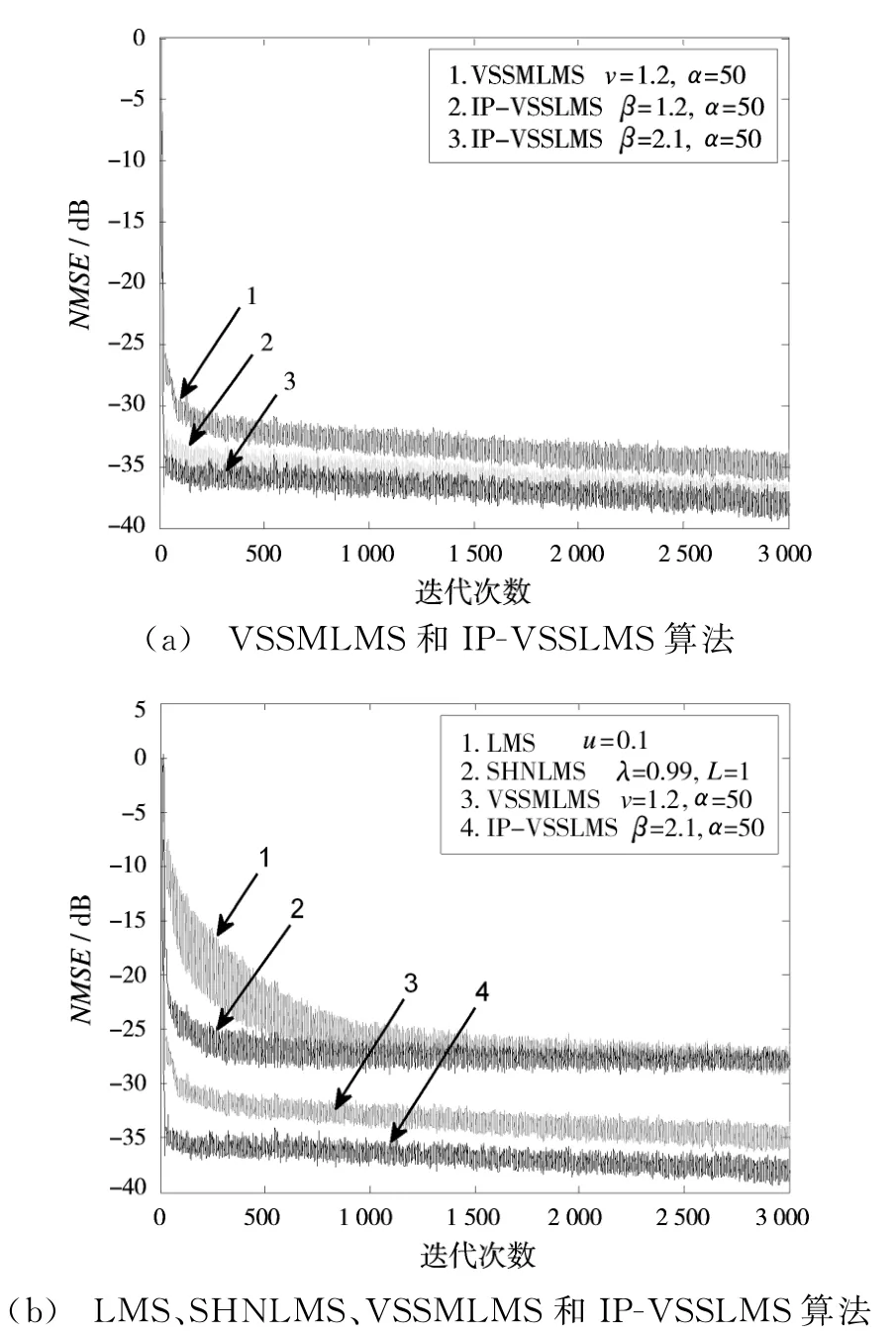
图3 归一化均方误差

为了进一步表明IP-VSSLMS预失真算法能够有效地解决非线性失真的问题,图4给出了有无预失真时信号的输出星座图。由图4可知,无预失真时信号出现了幅值失真和相位旋转,也就是出现了星座扭曲现象,这是由TWTA输入、输出信号之间的非线性引起的,而IP-VSSLMS预失真算法作用后幅值失真和相位旋转现象消失,由此可知,IP-VSSLMS预失真算法能够有效地解决信号的星座扭曲。

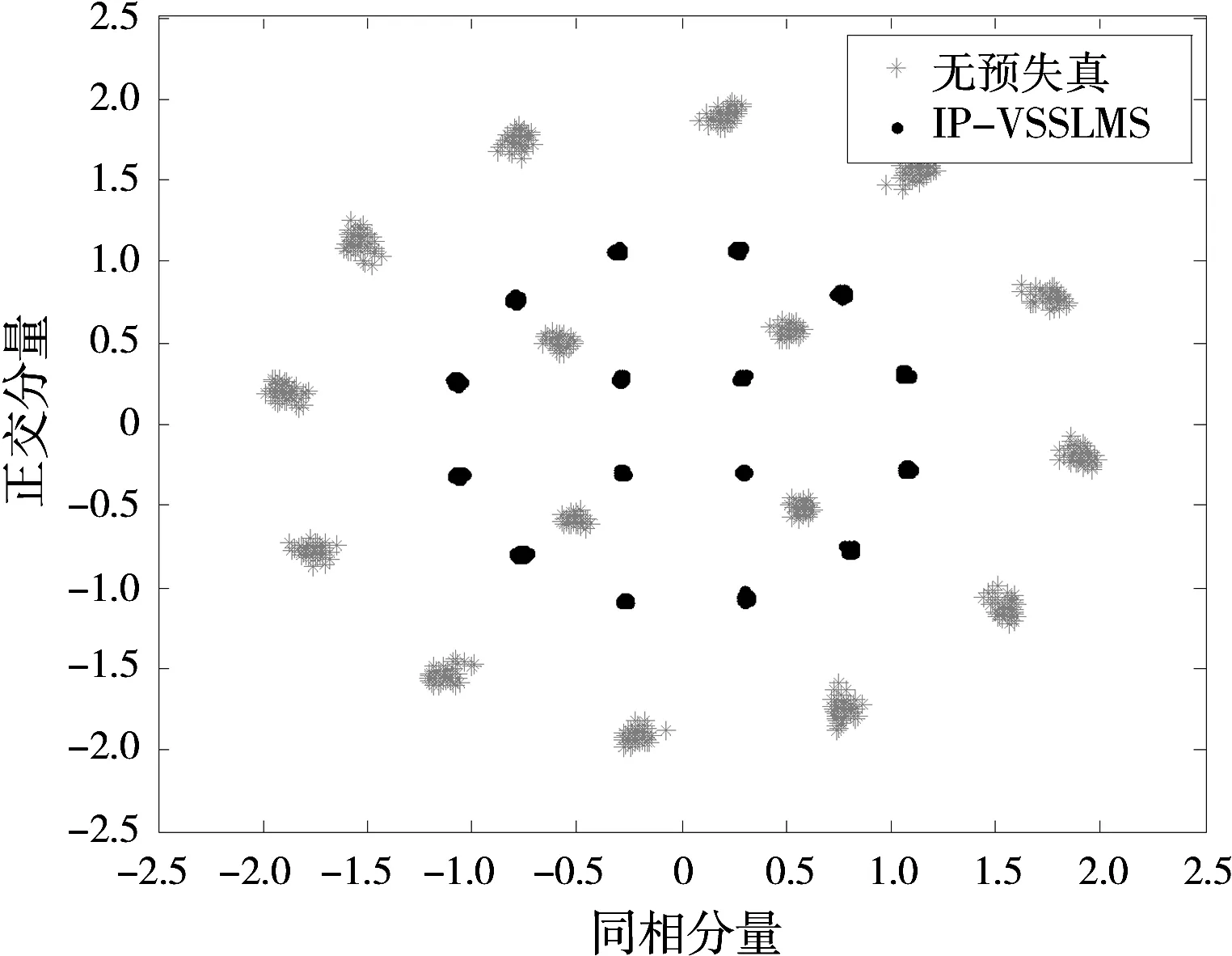
图4 星座图

从图5可知,无预失真时信号的频谱出现了频谱再生现象,而VSSMLMS算法和IP-VSSLMS算法作用时信号的频谱再生现象消失,并且相比VSSLMS算法,IP-VSSLMS算法的性能更加有效。由此可知,IP-VSSLMS算法在解决频谱再生的同时具有一定的优越性。

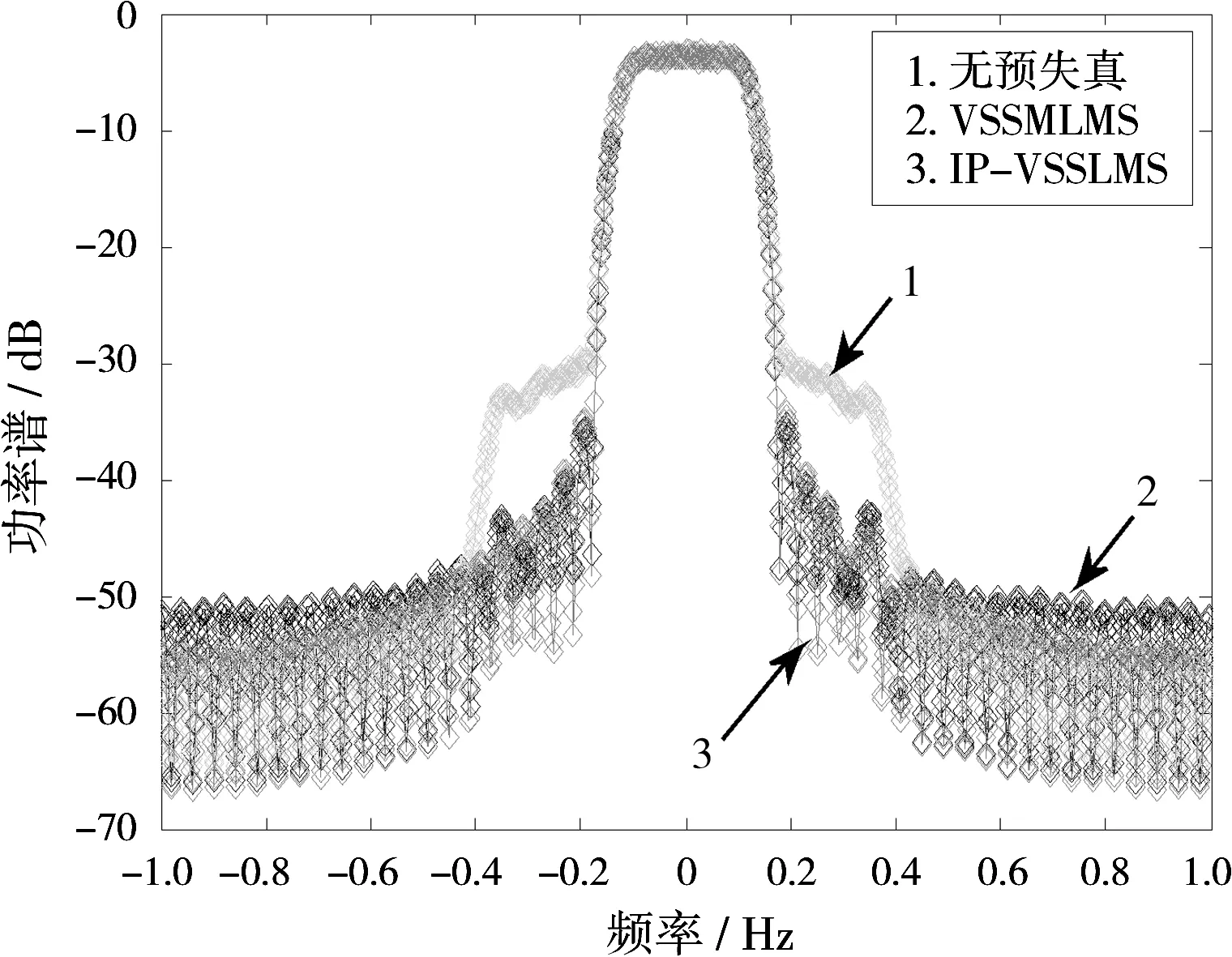
图5 功率谱

5 结束语

针对功率放大器非线性失真,以及LMS算法收敛速度慢和稳态误差大的缺点,提出了一种IPVSSLMS预失真算法。该算法通过使用误差信号,以及误差信号与输入信号的能量之和,构建了一种新的变步长收敛因子。仿真结果表明,在收敛速度和归一化均方误差方面,相比于LMS算法、SHNLMS算法和VSSMLMS算法,IP-VSSLMS算法能够获得较快的收敛速度和较小的归一化均方误差;在星座图方面,IP-VSSLMS算法能够有效地解决信号的星座扭曲现象;在功率谱方面,相比VSSMLMS算法,IP-VSSLMS能够更加有效地解决频谱再生的问题。综合以上分析可知,IPVSSLMS算法具有较好的应用价值。

[1]DELEU T,DERVIN M,KASAI K,et al.Iterative Predistortion of the Nonlinear Satellite Channel[J].IEEE Trans on Communications,2014,62(8):2916-2926.

[2]唐成凯,廉保旺,张玲玲.卫星通信中动态神经网络预失真算法研究[J].西北工业大学学报,2013,31(1):34-39.TANG Chengkai,LIAN Baowang,ZHANG Lingling.Dynamic Neural Network Based Pre-Distortion in Satellite Communication[J].Journal of Northwestern Polytechnical University,2013,31(1):34-39.(in Chinese)

[3]EUN C,POWERS E J.A New Volterra Predistorter Based on the Indirect Learning Architecture[J].IEEE Trans on Signal Processing,1997,45(1):223-227.

[4]张晓娟,吴长奇.使用变步长频域LMS算法的自适应Volterra均衡器[J].电路与系统学报,2012,17(4):99-102.ZHANG Xiaojuan,WU Changqi.Adaptive Volterra Equalizer Based on Variable Step-Size Frequency Domain LMS[J].Journal of Circuits and Systems,2012,17(4):99-102.(in Chinese)

[5]刘顺兰,蒋树南.非线性信道的均衡算法研究[J].电子学报,2010,38(10):2219-2223.LIU Shunlan,JIANG Shunan.Equalization Algorithms Based on Nonlinear Channel[J].Acta Electronica Sinica,2010,38(10):2219-2223.(in Chinese)

[6]KARAM G,SARI H.Analysis of Predistortion,Equalization,and ISI Cancellation Techniques in Digital Radio Systems with Nonlinear Transmit Amplifiers[J].IEEE Trans on Communications,1989,37(12):1245-1253.

[7]MORGAN D R,MA Z X,KIM J,et al.A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers[J].IEEE Trans on Sig-nal Processing,2006,54(10):3852-3860.

[8]ABD-ELRADY E,GAN L,KUBIN G.Predistortion of Hammerstein and Wiener Systems Using the Nonlinear Filtered-x Prediction Error Method Algorithm[J].E&I Elektrotechnik Und Informationstechnik,2010,127(10):285-290.

[9]ABD-ELRADY E,GAN L,KUBIN G.A Nonlinear Filtered-x Prediction Error Method Algorithm for Digital Predistortion in Digital Subscriber Line Systems[J].International Journal of Communication Systems,2013,26(5):651-661.

[10]QIAN H,YAO S J,HUANG H,et al.A Low-Complexity Digital Predistortion Algorithm for Power Amplifier Linearization[J].IEEE Trans on Broadcasting,2014,60(4):670-678.

[11]王红梅,李华强,王健铠,等.基于DOA估计的RLSCMA算法[J].雷达科学与技术,2014,12(3):315-320.WANG Hongmei,LI Huaqiang,WANG Jiankai,et al.A RLS-CMA Algorithm Based on DOA[J].Radar Science and Technology,2014,12(3):315-320.(in Chinese)

[12]BHOTTO M Z A,ANTONIOU A.A Family of Shrinkage Adaptive-Filtering Algorithms[J].IEEE Trans on Signal Processing,2013,61(7):1689-1697.

[13]ZHANG F,WANG Y,AI B.Variable Step-Size MLMS Algorithm for Digital Predistortion in Wideband OFDM Systems[J].IEEE Trans on Consumer Electronics,2015,61(1):10-15.