基于功率控制的分布式检测融合算法∗
(南京航空航天大学雷达成像与微波光子技术教育部重点实验室,江苏南京210016)
0 引言
随着计算机技术、通信技术和微波集成电路的快速发展,以及现代战争复杂性的日益提高,越来越多的传感器被纳入一体化网络参与协同作战[1-2]。同时,在现代电子战和信息战条件下,面对日益复杂的战场电磁环境,综合利用多传感器的信息,在空间域进行多传感器信息融合,不仅可以提高系统的可靠性和生存能力,而且可以尽可能全面、准确地获取信息,这也是未来战争发展的必然趋势和要求。
近些年来,国内外学者对多传感器信息融合问题进行了大量的研究[3-12]。何友等全面、系统地研究了多传感器信息融合理论及在各领域应用的发展与最新研究成果,为信息融合理论的发展及应用奠定了坚实的基础[3];Zhang等采用散度表征系统的二元检测融合性能,通过优化各传感器与融合中心的通信发射功率,使系统的融合性能达到最优[4];Kim和Goodman则在文献[4]的基础上,提出了分布式多元假设检验的功率控制算法[5];文献[7]研究了多传感器融合中的最优功率分配问题,即在满足系统功率约束的条件下,通过优化配置各传感器与融合中心通信时的发射功率,最小化系统融合估计的均方误差(MSE)。上述结果表明,多传感器网络的分布式检测融合性能与网络中传感器的数目、各传感器的发射功率以及信道状态等参数有关。
理论上,多传感器网络中所包含的传感器节点数目越多、各传感器与融合中心进行融合时的发射功率越大、信道噪声越小,系统的融合性能就越高。但在实际中,各传感器节点能量和带宽有限,而且军事应用中对射频隐身性能的需求日益迫切,需要多传感器网络在达到预先设定的检测融合性能的条件下尽可能地减少发射功率。因此,不少学者针对这一问题进行了研究。现有的基于能效的多传感器分布式检测融合方法主要分为两种,一种是基于融合发射功率分配的方法[11-12],另一种是基于融合发射次序调度的方法[13-14]。文献[11-12]针对并行结构的无线传感器网络,提出了一种基于能效的分布式检测与功率分配算法,仿真结果表明,该算法可以有效地实现节能,进而延长无线传感器网络的使用寿命。Blum等则从调度各传感器节点向融合中心发射次序的角度出发,针对大规模传感器网络中的能效问题,提出了一种优化调度的分布式检测融合算法,该算法在保证系统融合性能的前提下,有效节省系统的能量消耗[13-14]。总的来说,上述文献都是针对确定环境下的多传感器分布式检测融合问题进行研究,而对含有不确定因素的分布式检测融合问题的研究还需进一步加强。
现代战场电磁环境日益复杂,常含有不确定因素,但不确定性不能简单地用随机性来描述,在这种情况下,模糊理论提供了良好的解决方法。自1965年Zadeh首次提出模糊集的概念以来[15],模糊理论得到了长足的发展和广泛的应用。2002年,Liu提出了可信性测度的概念[16]。随后,Liu又发展出了可信性理论的公理化体系[17],建立起一套模糊规划理论[18]。近年来,模糊机会约束规划(FCCP)在诸多领域都得到了广泛的应用,具有广阔的发展前景[19-21]。因此,本文针对现代战场电磁环境的复杂性和不确定性,提出了一种分布式检测融合中基于FCCP的发射功率分配算法。本文首先推导了表征系统检测融合性能的散度表达式。然后,引入可信性理论,将系统的散度门限看作梯形模糊变量,以最小化融合时各传感器与融合中心的发射功率为目标,在满足系统检测融合性能不小于给定门限的概率超过某一置信水平的条件下构建FCCP模型,并采用基于非线性规划的遗传算法(NPGA)对该非凸、非线性模型进行求解。最后,仿真结果验证了本文算法的可行性和有效性,并分析了传感器及信道参数对系统发射功率分配的影响。
1 基本概念与模型
1.1 可信性理论基本概念
定义1[16]设Θ是一个非空集合,P是Θ的幂集。如果集函数Cr满足下面的条件:
(1)Cr{Θ}=1;
(2)如果A⊂B,则Cr{A}≤Cr{B};
(3)Cr是自对偶的,即对于任意的A∈P,有Cr{A}+Cr{Ac}=1;
(4)对于P中任意集族{A i},如果supiCr{A i}<0.5,则Cr{∪i A i}=supiCr{A i},则称Cr为可信性测度。此时,称三元组(Θ,P,Cr)为一个可信性空间。
定义2[17]如果ξ是定义在可信性空间(Θ,P,Cr)上的模糊变量,则它的隶属函数定义为

定义3[22]假设ξ为模糊变量,若函数Φ:[-∞,+∞]→[0,1]满足:

则Φ称为模糊变量ξ的可信性分布。也就是说,可信性分布Φ(x)是模糊变量ξ取值小于或等于x的可信性。
1.2 系统模型
考虑由Nt部传感器与一个融合中心构成的分布式二元假设检验问题,如图1所示。Nt个传感器节点R1,…,R Nt在收到未经处理的原始数据X1,…,X Nt之后,各节点分别作出局部检测判决U1,…,U Nt,然后经无线数据链将局部检测判决传输至融合中心,进而在融合中心得到全局决策U0。

图1 多传感器分布式检测融合模型
假设Nt部传感器节点的观测值统计独立,可构成观测向量X=[X1,…,X Nt]T。各传感器节点独立进行判决f i(·),局部判决向量U=[U1,…,U Nt]T,且有

于是,局部判决的联合条件概率密度函数[21]可
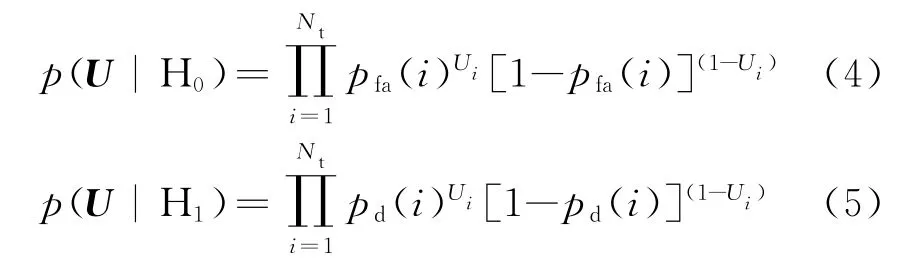
式中,pd(i),pfa(i)分别为传感器i的检测概率与虚警概率。
各传感器节点的局部判决经正交信道传输至融合中心,则融合中心经由无线正交信道接收来自传感器节点的信号可以表示为

式中,Y=[Y1,…,Y Nt]T表示融合中心处接收到的信号表示正交信道增益表示传感器与融合中心进行通信的信号放大倍数,其中,Pti为传感器i的通信发射功率,n=[n1,…,n Nt]T表示均值为0的信道加性高斯噪声,其协方差矩阵为Rθ=
在给定各传感器发射信号U的情况下,融合中心处接收信号Y的条件概率密度函数为

因此,可以得到

最后,融合中心利用融合准则f0(·)得到的全局判决可以表示为

2 基于FCCP的发射功率分配算法
2.1 问题建模

式中,D(·)表示Kullback-Leibler(KL)散度。
为简化计算,假设p(Y|Hi)服从高斯分布N(Y;ηi,Ξi),则对于i∈ {0,1},有

由于pd(i)≫pfa(i)(∀i),由式(15)可得
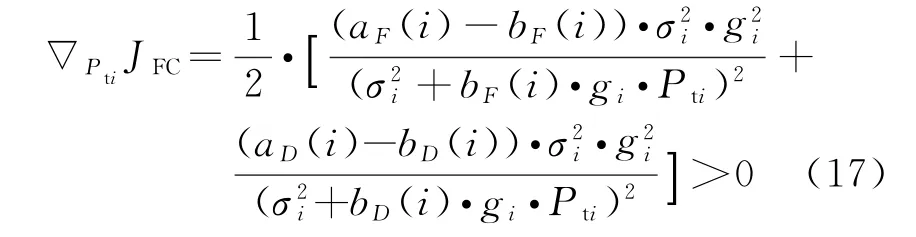
式中,∇Pti JFC表示函数JFC对第i部传感器发射功率Pti的一阶偏导。从式(17)可以看出,函数JFC关于正数Pti的一阶偏导是正的,因此,JFC与传感器的发射功率Pti成正比。

式中,Jth为表征系统检测融合性能的散度门限,为第i部传感器发射功率的上限。式(18)模型的目的是在达到预先设定的融合性能散度门限的前提下,对系统进行检测融合的发射功率资源进行合理分配,使其消耗的功率最少。但由于战场电磁环境的复杂性和不确定性,系统融合性能散度门限会根据战场任务的不同具有一定的不确定性。在不确定的条件下,将功率资源分配构建为确定性模型很难保证算法的稳健性和可靠性[21]。

式中,Cr{·}为事件{·}的可能性,α为预先给定的置信水平,其取值依赖于决策者的主观性和偏好[20]。因此,得到分布式检测融合时优化分配发射功率的FCCP模型为
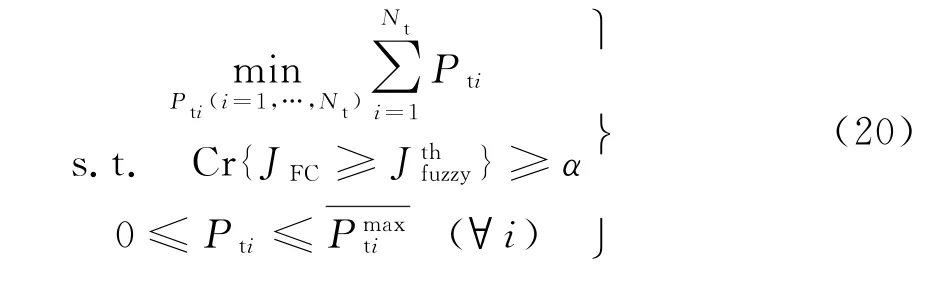
式(20)模型的含义是在约束条件成立的可信性不小于决策者预先给定的置信水平时,通过对系统发射功率资源进行最优分配,使得系统总发射功率最小化。
由式(20)模型可知,若置信水平α越小,可行解集就越大,那么系统消耗的总功率就可能越小,但同时不满足约束条件的概率也越大;反之,若置信水平α越大,可行解集就变小,那么系统消耗的总功率就可能越大,但不满足限制条件的概率就越小。也就是说,系统的发射功率与置信水平之间存在着制约关系。
2.2 模型求解
2.2.1 FCCP模型的清晰等价形式

定理1[18]:设ξ=(r1,r2,r3,r4)为一梯形模糊变量,则对任意给定的置信水平α,0<α≤1,则:
根据以上定理,可得

则式(20)模型可转化为清晰等价形式:

2.2.2 NPGA求解
根据式(24)模型,定义目标函数:

由式(15)可以看出,JFC是Pti的非凸、非线性函数,不存在闭式解析表达式,其可控参数中各传感器发射功率的取值可以考虑采用穷举法求解,虽简单易行但求解效率太低。遗传算法采用选择、交叉和变异算子进行搜索,全局搜索能力较强,但是局部搜索能力较弱,一般只能得到问题的次优解,而不是最优解。经典的非线性规划算法大多采用梯度下降的方法求解,局部搜索能力较强,但是全局搜索能力较弱。本文采用NPGA进行求解[25],一方面用遗传算法进行全局搜索,另一方面采用非线性规划算法进行局部搜索,以得到问题的全局最优解。NPGA流程图如图2所示。

图2 NPGA流程图
3 仿真结果及分析
为了验证基于FCCP的发射功率分配算法的可行性和有效性,并进一步分析传感器及信道参数对系统发射功率分配的影响,本文进行了如下仿真。现假设传感器数目Nt=4,检测概率pd(i)=0.9,虚警概率pfa(i)=10-6,信道噪声方差10-12W=-90 dBm,信道增益g i=1.5×10-13=-128 d B,i=1,…,Nt。根据经验及仿真实验数据,设梯形模糊数为
采用NPGA求解式(24)模型,其中,设置进化代数为30,种群规模为100,交叉概率为0.6,变异概率为0.01。为了分析不同置信水平对系统发射功率分配的影响,将置信水平α分别设置为0.60,0.80,0.90,0.99。图3和图4分别给出了在不同的检测概率和虚警概率条件下,不同置信水平对系统发射功率分配的影响。在图3中,假设各传感器的检测概率分别为pd(1)=0.75,pd(2)=0.8,pd(3)=0.85,pd(4)=0.9;在图4中,假设各传感器的虚警概率分别为pfa(1)=10-6,pfa(2)=10-3,pfa(3)=0.02,pfa(4)=0.05。仿真结果表明,发射功率较多地分配给检测概率高、虚警概率低的传感器节点,而对于检测概率低、虚警概率高的传感器,则分配较少的发射功率,从而在保证系统检测融合性能的前提下,有效地节省发射总功率。另外,置信水平越高,系统节省的发射功率越少。也就是说,每部传感器进行融合时发射的功率越多,不满足系统性能约束条件的概率就越小,置信水平也就越高。
图5和图6分别给出了在不同的信道噪声方差和信道增益条件下,不同置信水平对系统发射功率分配的影响。在图5中,假设各信道噪声方差分别为在图6中,假设各信道增益分别为g1=1.5×10-13,g2=2.5×10-13,g3=4×10-13,g4=2×10-13。结果显示,发射功率倾向于分配给信道噪声方差小、信道增益大的传感器,而对于信道噪声方差大、信道增益小的传感器,则分配较少的发射功率,甚至关闭信道状态不好的传感器节点,使其不参与功率分配,从而有效地节省了系统的功率资源。
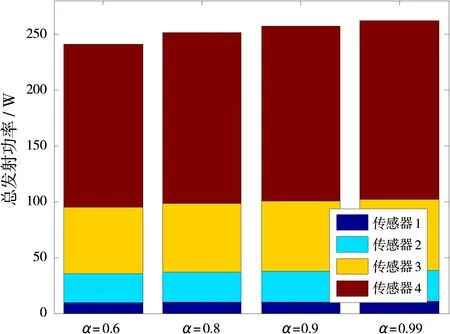
图3 在不同的检测概率条件下不同置信水平对系统发射功率分配的影响
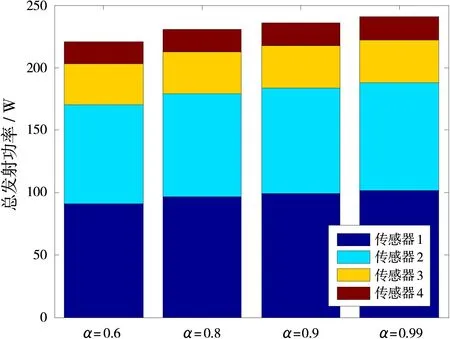
图4 在不同的虚警概率条件下不同置信水平对系统发射功率分配的影响

图5 在不同的信道噪声方差条件下不同置信水平对系统发射功率分配的影响
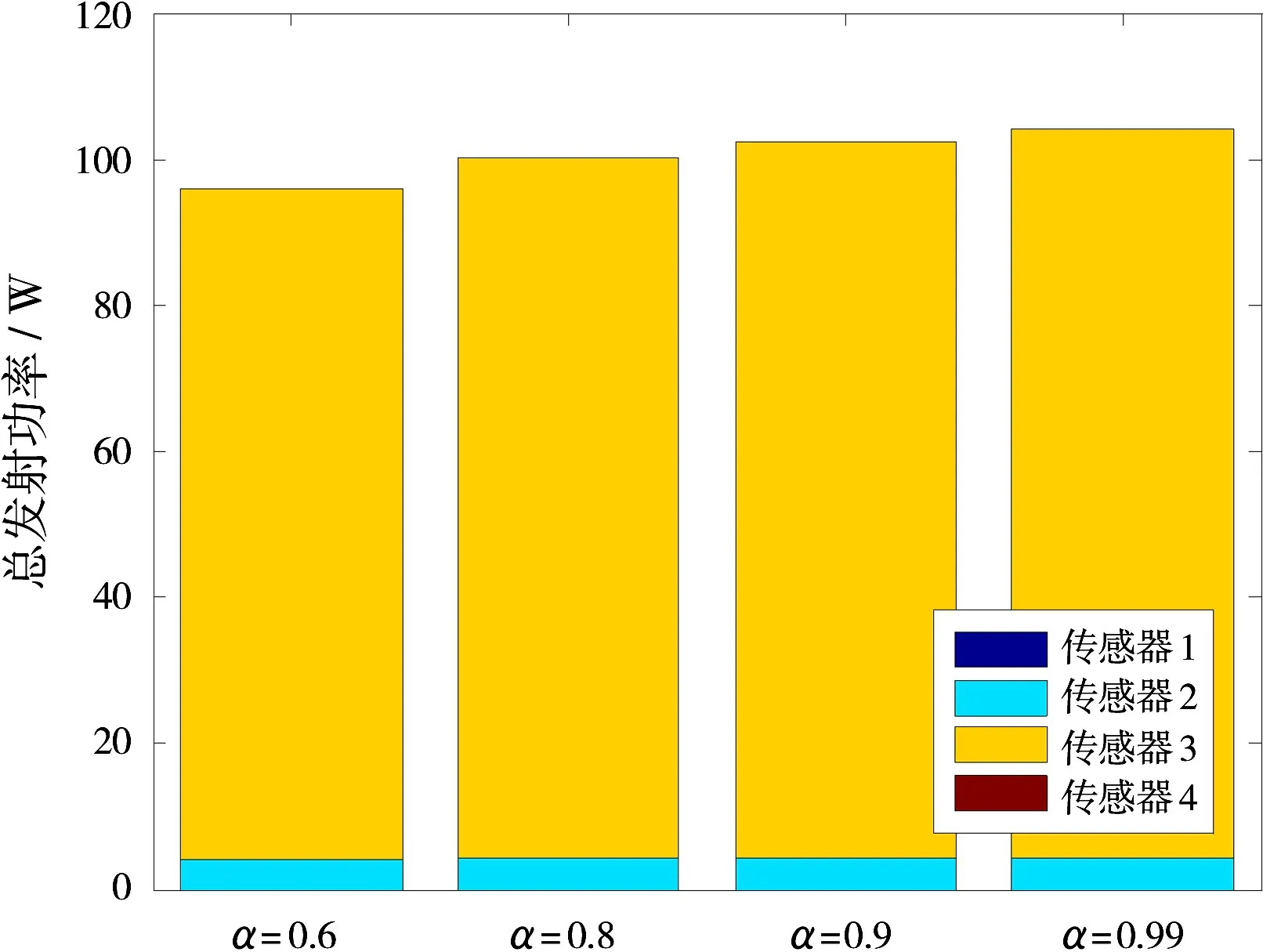
图6 在不同的信道增益条件下不同置信水平对系统发射功率分配的影响
图7给出了不同条件下,本文所提算法与功率均匀分配情况的对比。从图中可以看出,在不同的置信水平下,本文算法与均匀分配算法相比,大致可以节省5%~25%的功率资源,节省的功率大小与传感器的检测概率、虚警概率、信道噪声方差和信道增益有关。而且,置信水平越高,不满足FCCP约束条件的概率就越小,系统消耗的总功率也就越多。
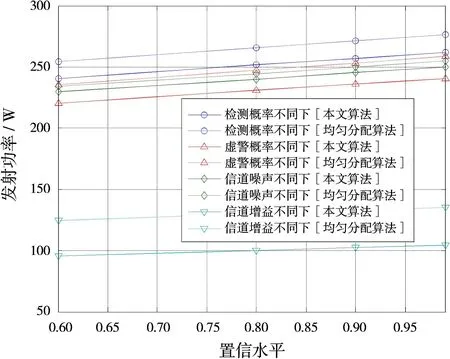
图7 在不同条件下本文算法与功率均匀分配的对比
从上述仿真结果可以看出,在保证一定检测融合性能的前提下,均匀分配算法比本文所提算法要消耗更多的发射功率。系统的功率分配与传感器的检测概率、虚警概率、信道噪声方差和信道增益有关,在分配过程中,发射功率倾向于分配给传感器检测概率高、虚警概率低、信道噪声方差小和信道增益大的传感器。多传感器分布式检测融合系统可根据各传感器性能及信道状态,动态地调整各传感器与融合中心的发射功率,使其在保证一定的检测融合性能的条件下,有效地节约系统的功率资源。另外,置信水平越高,系统的发射功率也就越大,置信水平与系统的发射功率两者之间存在着制约关系。
4 结束语
本文针对分布式多传感器检测融合系统,提出了一种基于FCCP的发射功率分配算法,将表征系统检测融合性能的散度门限看作模糊变量,建立FCCP模型,并采用NPGA进行求解。所提算法可使系统动态调整融合时各传感器与融合中心的发射功率,在满足模糊机会约束的条件下,尽可能地节省总发射功率。仿真结果表明,相比于均匀分配功率的情况,本文所提算法可有效节省系统的发射功率。值得注意的是,本文中假设各传感器的检测概率与虚警概率均已知,这在实际的战场环境下是很难保证的。当各传感器的检测概率和虚警概率均模糊时的最优功率分配算法将是下一步的研究重点。
[1]刘钦.多传感器组网协同跟踪方法研究[D].西安:西安电子科技大学,2013:1-10.
[2]熊年生.基于分布式检测的雷达组网探测技术研究[J].雷达科学与技术,2012,10(4):363-366,371.XIONG Niansheng.Research on Radar Coordinated Eetection Scheme Based on Distributed Detection Technique[J].Radar Science and Technology,2012,10(4):363-366,371.(in Chinese)
[3]何友,王国宏,关欣,等.信息融合理论及应用[M].北京:电子工业出版社,2010:91-134.
[4]ZHANG X,POOR H V,CHIANG M.Optimal Power Allocation for Distributed Detection over MIMO Channels in Wireless Sensor Networks[J].IEEE Trans on Signal Processing,2008,56(9):4124-4140.
[5]KIM H,GOODMAN N A.Power Control Strategy for Distributed Multiple-Hypothesis Detection[J].IEEE Trans on Signal Processing,2010,58(7):3751-3764.
[6]AHMADI H R,VOSOUGHI A.Optimal Training and Data Power Allocation in Distributed Detection with Inhomogeneous Sensors[J].IEEE Signal Processing Letters,2013,20(4):339-342.
[7]ALIREZAEI G,REYER M,MATHAR R.Optimum Power Allocation in Sensor Networks for Passive Radar Applications[J].IEEE Trans on Wireless Communications,2014,13(6):3222-3231.
[8]CIUONZO D,PAPA G,ROMANO G,et al.One-Bit Decentralized Detection with a Rao Test for Multisensor Fusion[J].IEEE Signal Processing Letters,2013,20(9):861-864.
[9]WENG Z Y,DJURIC P M.Data Fusion Based on Convex Optimization[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,Vancouver,BC:IEEE,2013:6605-6609.
[10]CIUONZO D,SALVO ROSSI P.Decision Fusion with Unknown Sensor Detection Probability[J].IEEE Signal Processing Letters,2014,21(2):208-212.
[11]CUI Shuguang,XIAO Jinjun,GOLDSMITH A J,et al.Estimation Diversity and Energy Efficiency in Distributed Sensing[J].IEEE Trans on Signal Processing,2007,55(9):4683-4695.
[12]郭晓冬,杜鹏,张雪芬.一种WSN中能量有效的分布式检测和功率分配算法[J].山东大学学报(理学版),2012,47(9):60-64.GUO Xiaodong,DU Peng,ZHANG Xuefen.A Energy-Efficient Distributed Detection and Power Allocation Algorithm in Wireless Sensor Networks[J].Journal of Shandong University(Natural Science),2012,47(9):60-64.(in Chinese)
[13]YANG Yang,BLUM R S,SADLER B M.Distributed Energy-Efficient Scheduling for Radar Signal Detection in Sensor Networks[C]∥IEEE Radar Conference,Washington,DC:IEEE,2010:1094-1099.
[14]BLUM R S.Ordering for Energy Efficient Estimation and Optimization in Sensor Networks[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,Prague,Czech Republic:IEEE,2011:2508-2511.
[15]ZADEH L A.Fuzzy Sets[J].Information and Control,1965,8(3):338-353.
[16]LIU Baoding,LIU Yiankui.Expected Value of Fuzzy Variable and Fuzzy Expected Value Models[J].IEEE Trans on Fuzzy Systems,2002,10(4):445-450.
[17]LIU Baoding.Uncertainty Theory:An Introduction to Its Axiomatic Foundations[M].Berlin:Spring-Verlag,2004:109-128.
[18]刘宝碇,赵瑞清,王纲.不确定规划及应用[M].北京:清华大学出版社,2003:138-187.
[19]吴杰康,唐力.基于模糊机会约束规划的水火电力系统多目标随机调度模型[J].中国电机工程学报,2011,31(25):26-34.WU Jiekang,TANG Li.Multi-Objective Stochastic Scheduling Models for Hydrothermal Plants Based on Fuzzy Chance Constrained Programming[J].Proceedings of the CSEE,2011,31(25):26-34.(in Chinese)
[20]龚树凤,贲德,潘明海,等.基于模糊机会约束规划的机会阵雷达方向图综合[J].航空学报,2014,35(9):2615-2623.GONG Shufeng,BEN De,PAN Minghai.et al.Pattern Synthesis for Opportunistic Array Radar Based on Fuzzy Chance-Constrained Programming[J].Acta Aeronautica et Astronautica Sinica,2014,35(9):2615-2623.(in Chinese)
[21]严峻坤,刘宏伟,戴奉周,等.基于非线性机会约束规划的多基雷达系统稳健功率分配算法[J].电子与信息学报,2014,36(3):509-515.
[22]LIU Baoding.Theory and Practice of Uncertain Programming[M].Heidelberg:Physical-Verlag,2002:53-74.
[23]SHI C G,WANG F,SELLATHURAI M,et al.LPI Optimization Framework for Target Tracking in Radar Network Architectures Using Information-Theoretic Criteria[J].International Journal of Antennas and Propagation,2014(2014):1-10.
[24]BOYD S,VANDENBERGHE L.Convex Optimization[M].Cambridge:Cambridge University Press,2004:71-74.
[25]史峰,王辉,郁磊,等.MATLAB智能算法:30个案例分析[M].北京:北京航空航天大学出版社,2011:17-26.

