CFETR中心螺线管模型线圈磁场及电磁载荷计算

杜世俊(1950-),男,安徽合肥人,博士,中国科学院等离子体物理研究所教授, 博士生导师.

CFETR中心螺线管模型线圈磁场及电磁载荷计算

季峰,杜世俊,刘小刚,王兆亮

(中国科学院 等离子体物理研究所,安徽 合肥230031)

摘要:中国聚变工程实验堆的中心螺线管模型线圈由Nb3Sn、NbTi混合超导磁体组成,在初始设计阶段,需要进行大量的探索计算以获得设计方案。文章基于微元叠加法原理,利用Matlab的向量化编程,提出了一种可修改性强、计算时间短的磁场计算方法,并将计算结果与有限元法进行对比,证实了本方法是可行的,并提高了设计效率,同时给出了线圈电磁载荷的分布情况。

关键词:中国聚变工程实验堆;中心螺线管;磁场计算;微元法;电磁载荷

基金项目：国家973计划资助项目(2014GB105002)

作者简介：季峰(1989-),男,江苏泰兴人,中国科学院等离子体物理研究所硕士生;

doi:10.3969/j.issn.1003-5060.2015.06.014

中图分类号:TM551文献标识码：A

收稿日期：2014-05-14；修回日期：2015-06-10

MagneticfieldandelectromagneticloadcalculationforCFETRcentralsolenoidmodelcoil

JIFeng,DUShi-jun,LIUXiao-gang,WANGZhao-liang

(InstituteofPlasmaPhysics,ChineseAcademyofSciences,Hefei230031,China)

Abstract:Thecentralsolenoid(CS)modelcoilofChinaFusionEngineeringTestReactor(CFETR)ismadeupofNb3Sn and NbTi hybrid superconducting magnet. At the beginning of design, large amounts of exploratory calculation are essential to get the optimal plan. Based on the infinitesimal method, a new method for calculating the magnetic field is presented using the vectorized programming by Matlab. This program is changeable and can make the calculating speed much faster. The result of this method is compared with the FEM, which proves that this method is feasible and can improve the efficiency of the design. The electromagnetic load distribution is also given.

Keywords:ChinaFusionEngineeringTestReactor(CFETR);centralsolenoid(CS);magneticfieldcalculation;infinitesimalmethod;electromagneticload

中国聚变工程实验堆(ChinaFusionEngineeringTestReactor,CFETR)是我国即将开展的类ITER聚变工程试验堆[1]。装置运行时等离子体所需的伏秒数主要由中心螺线管(CentralSolenoid,CS)线圈提供,因此CS线圈的设计尤为重要。由于CFETR采用大型低温超导CS线圈,国内尚不具备相关制造经验,因此需要首先设计、制造一个模型线圈以积累经验，并对其性能进行实验分析。

CFETR的CS模型线圈正常工作时背景磁场最高达12T,最大磁场变化率为1.5T/s。常规的NbTi超导线在4.2K温度下的临界磁场约为11T,无法满足要求,因此选用在此温度下临界磁场为20T的Nb3Sn超导线[2]。考虑到Nb3Sn线的造价约为NbTi的5倍,因此在线圈外围磁场较低处仍然使用NbTi超导线。在此条件下,CS模型线圈采用混合导体模式,内外线圈分别由Nb3Sn、NbTi导体绕制而成,2种导体均为导管内多级绞缆导体,即CICC(Cable-In-Conduit Conductor)导体[3]。

本文基于微元法提出了分析双层超导线圈周围磁场分布的方法,并与Ansoft有限元仿真结果进行了比较,说明了该方法的优点,并根据计算所得磁场给出了电磁载荷的分布。

1CS线圈设计要求及模型

CS模型线圈采用的Nb3Sn和NbTi单根导体均为内圆外方的CICC导体,其尺寸分别为492×φ32.6和51.92×φ35.3[4-5]。

CS模型线圈的初步设计要求是在最大运行电流小于50kA的条件下产生最大值12T的磁感应强度。Nb3Sn线材需要经过热处理才能形成超导相,而中科院强磁场中心的热处理炉的温度均匀区外半径是1 m,这就要求Nb3Sn线圈外半径小于1 m。NbTi则不需要热处理,但是其超导临界磁场较低,在考虑足够的安全裕度的情况下,要求其背景磁场小于6 T。

经过大量的试探性计算和分析后,磁体的初步设计模型如图1所示,表1所列为内外线圈的主要结构设计参数,内外线圈运行电流均为49kA。

图1　 CS模型线圈

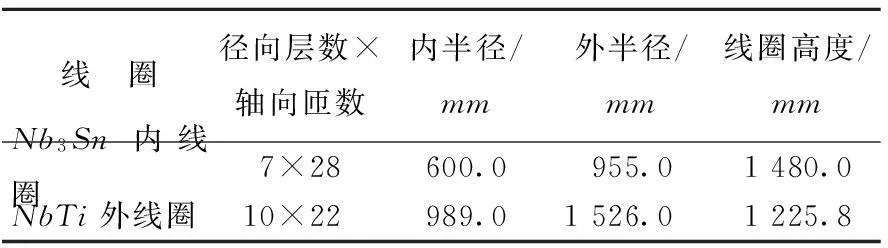
线 圈径向层数×轴向匝数内半径/mm外半径/mm线圈高度/mmNb3Sn内线圈7×28600.0955.01480.0NbTi外线圈10×22989.01526.01225.8

2磁场计算方法及结果

2.1　微元法计算圆环电流磁场原理

线圈模型轴对称,因此可以根据圆环电流产生的磁场来计算磁感应强度。首先计算单匝线圈作用下的磁场，如图2所示。

图2中，假设线圈与xoy平面平行,圆心位于z轴上O′点,半径为r0,电流为I。根据轴对称可知空间中任意处磁场与其环向角无关,且磁场的环向分量Bθ为0,因此不妨取xoz平面内点P(x,0,z)。以线圈圆心角θ为变量,则线圈上任意源点P′(x0,y0,z0)处的电流元可表示为:

Idl=(Ir0dθ)eθ=

P′点坐标亦可用θ的函数P′(r0cosθ,r0sinθ,z0)来表示。

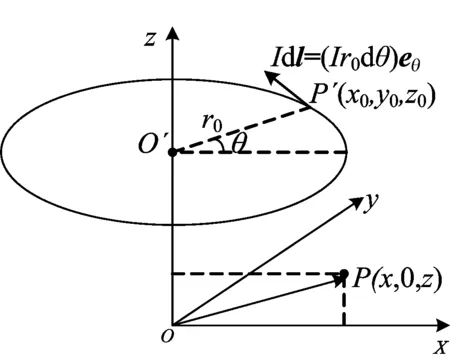
图2　圆环电流在空间产生磁场计算示意图

对于空间中任意场点P(x,0,z),源点与其之间的方向矢量为r=(x-x0)ex-y0ey+(z-z0)ez,根据毕奥-沙伐定律[6],源点在场点产生的磁场为:

(1)

将(1)式展开可得:

(2)

其中r=[(x-r0cosθ)2+(r0sinθ)2+(z-z0)2]1/2。

对于xoz平面内任意点磁场,在Bθ=0时,将直角坐标系转化为柱坐标系有Bx=Br、By=0、Bz=Bz。因此对(2)式中dBx、dBz积分可求得P点Br、Bz,进而求出P点场强。在Matlab中,为避免积分带来的大量的计算量,用微元叠加法来代替积分计算。取dθ=2π/180为步长,在[dθ,2π]区间上对(2)式进行叠加:

(3)

同理,进行合适的网格划分后,即可得出场域内的磁场分布、最大磁场及其位置,以及测试NbTi区的磁场是否超过设计要求。

2.2　计算过程及结果

在设计过程中,为了达到12T的最大磁场,同时使用最少的Nb3Sn导体,并使得NbTi线圈背景磁场小于6T,需要不断地修改内外线圈的匝数、层数以及内径,因此对程序的易修改性和计算速度要求比较高,本文尽可能多地利用Matlab数组/矩阵运算指令代替包含标量运算表达式的循环体,提高了程序的可读性和执行速度。

由于线圈模型的轴对称和上下对称特性,取线圈截面的1/2进行分析,如图3所示(单位为mm)，对图3中框内场域进行分析计算[7-8]。

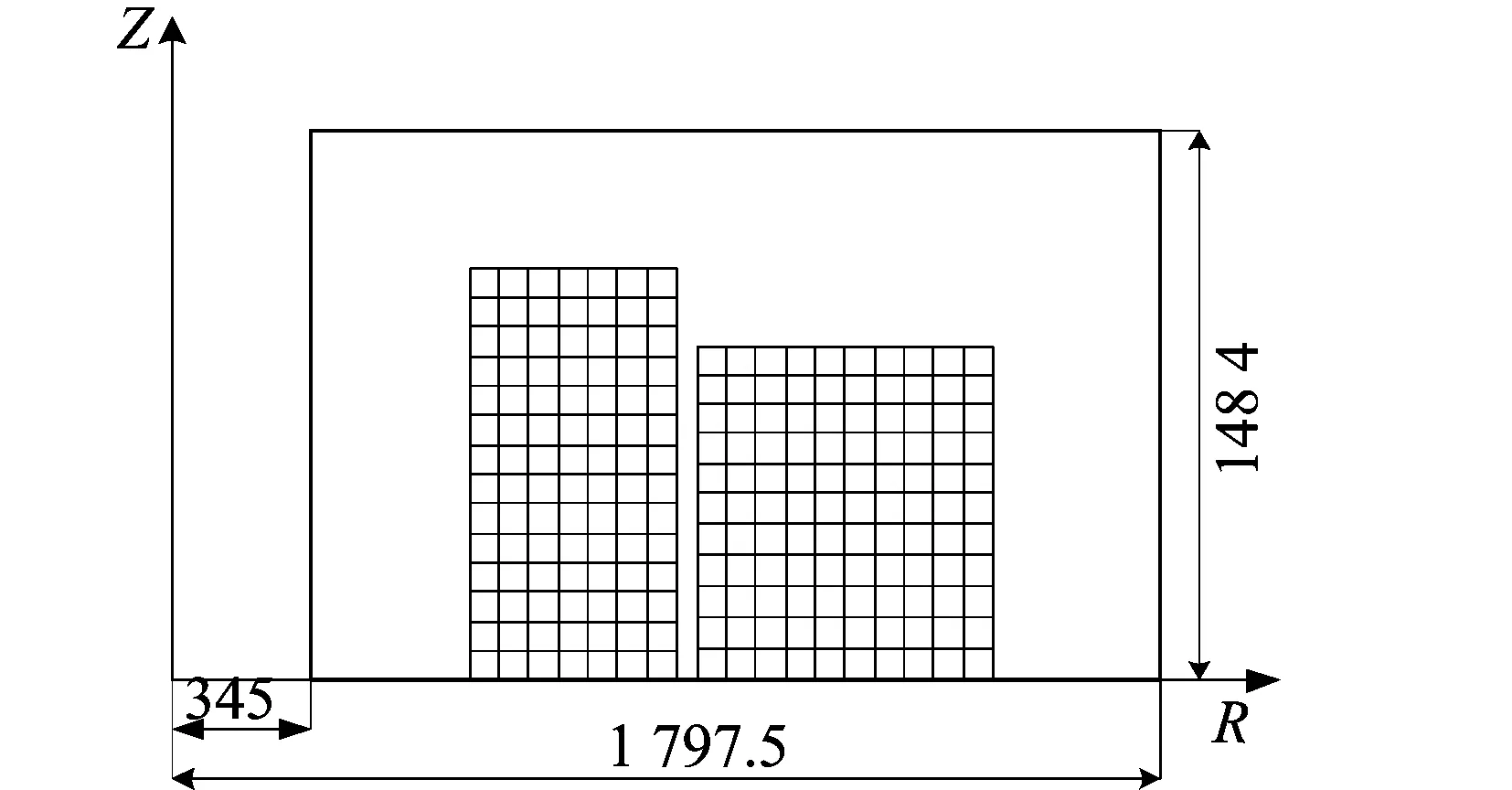
图3　 CS模型1/2截面简图

在划分场点网格时,为了能够取到磁场最大的点,同时避免场点和电流源点重合发生计算错误,对线圈单根导管单元划分方法如图4所示。

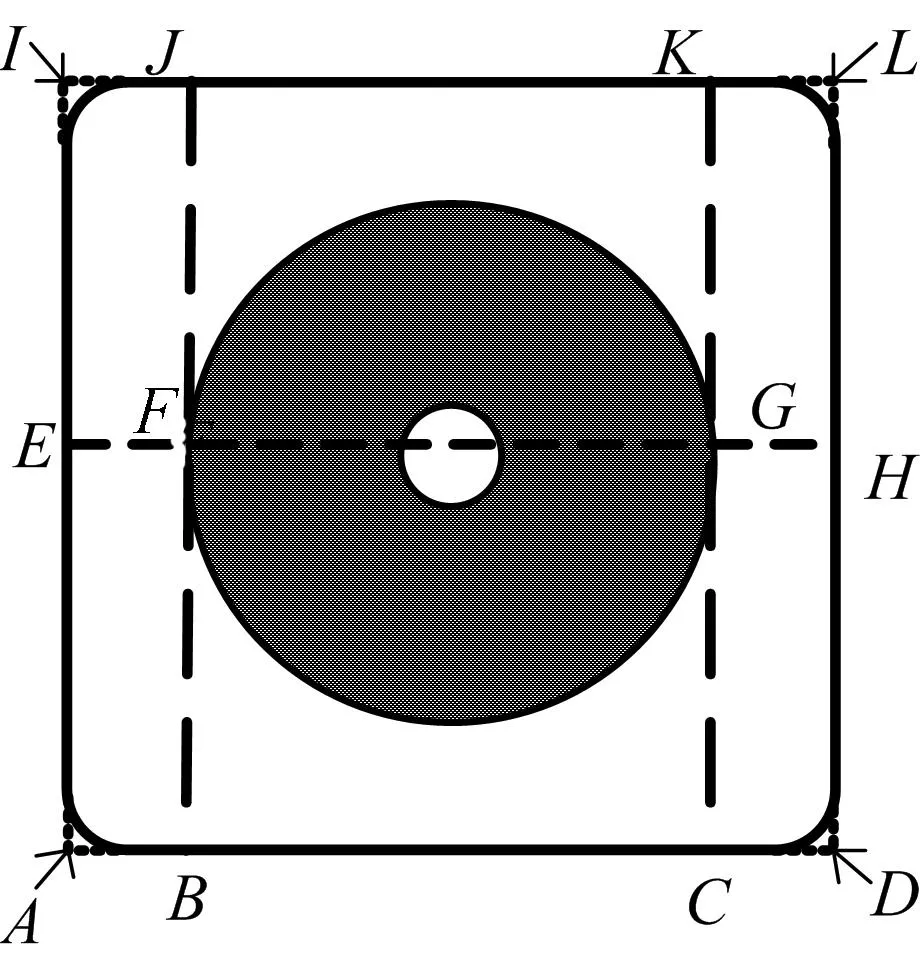
图4　单导管网格划分示意图

图4中，4条边上的场点与相邻导管共用。在线圈外场域,345mm≤R≤955mm区域内网格按Nb3Sn网格尺寸划分,989 mm≤R≤1 797.5mm区域按NbTi网格尺寸划分。

将网格划分后的场点坐标存入X、Y、Z向量中,根据(3)式进行向量化编程计算,这样可以大大减少循环的次数。在设计更改的过程中,只需要更改内外线圈的匝数、层数以及内外半径,网格可以根据这些输入量自动更改,提高工作效率。

将计算得出的场域内的磁感应强度进行矩阵变换得出横截面上磁场等势图如图5所示,其中整个场域内最大磁场为11.967T,NbTi部分最大磁场为5.925T,符合设计要求,计算时间为22.5s。图6所示为磁感应强度在不同高度上沿径向变化曲线以及在不同半径上沿轴向变化曲线。

图5　磁场等势图

图6　微元法磁感应强度变化图

结合图5和图6可以看出,整个线圈模型背景磁场最大处位于Nb3Sn最内层轴向中心处,最小处位于NbTi线圈内部。

在径向上,Nb3Sn区域的磁场随着半径增大逐渐减小;NbTi区域则是先减小后增大,在各匝线圈作用下,R=1.37m,z=0附近,磁场最小,趋于0。

在轴向,Nb3Sn区域的磁场随着线圈高度的增加而逐渐减小,到了非线圈区域,则急剧减小;NbTi区域磁场随着高度增加而增大,并在最内层线圈的最高处达到磁场最大值。

3Ansoft有限元仿真

Ansoft静磁场求解器中矢量磁位A满足:

(4)

其中,Az(x,y)为矢量磁位Z轴分量；Jz(x,y)为电流流动界面的电流密度；μ为材料的磁导率。将(4)式应用到有限元数值计算中,可以很容易求得矢量磁位A,通过B=×A即可求得静磁场的磁感应强度[9]。

在Ansoft中,建立面电流模型进行计算,将每匝导体作为独立的面电流源,建立好模型后,在求解域的上下边界和外边界施加气球边界条件,在内侧边界施加对称边界条件,划分网格后并求解,结果如图7所示。求得Nb3Sn处最大磁场为11.973 T,NbTi处最大磁场为5.938 T。

图7　Ansoft有限元仿真磁场分布云图

图8所示为Ansoft结果的磁场变化趋势,图8中a、b、c、d分别与图6相对应。通过对比可以发现,有限元法和数值计算法得出的结果高度吻合。

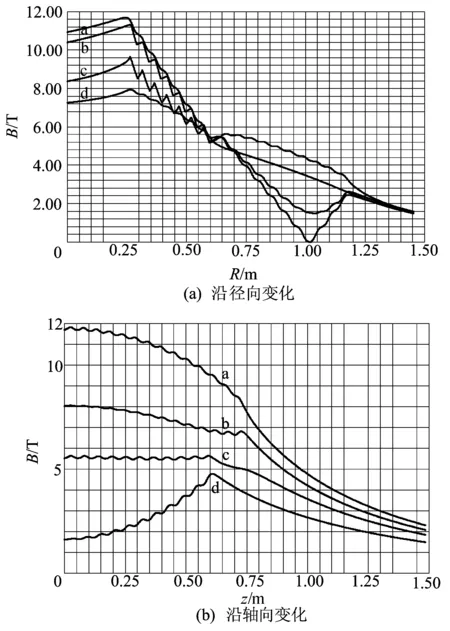
图8　有限元法磁感应强度变化图

4电磁载荷分布

线圈通电后在磁场作用下会产生电磁力,载流导体dl所受的电磁力为df=Idl×B。由此可知,轴向磁场Bz产生径向电磁力Fr=BzIl,径向磁场Bx产生轴向电磁力Fz=BxIl。

根据前文所得磁场计算出单位长度导体所受电磁力分布如图9所示。

其中数字为线圈径向层数编号,最内层为第1层,以此类推;在描述轴向电磁力时为了能清楚地显示曲线趋势,只画出了z>0部分线圈所受电磁力,z < 0部分与z> 0部分所受轴向电磁力大小相同,方向相反。

由图9可以看出,Nb3Sn在最内层线圈处所受径向电磁力Fr最大,该层Fz最大处可达550kN/m,由内层往外层依次减小,在同一层受到的Fr两端小,中间大;而轴向电磁力Fz分布趋势则和Fr相反,由内层向外层依次增大,同一层Fz两端大,中间小。NbTi所受Fz方向在第7层由于Bz方向的改变而随之变化;Fz从第1层到第3层增大,从第4层开始逐渐减小,第6层和第1层、第5层和第2层、第4层和第3层所受的Fz分别几乎相等。

图9　单位长度导体所受电磁力分布

最大磁场强度计算结果见表2所列，通过分析表2可以看出,基于微元法的数值算法和Ansoft有限元仿真得出的最大磁场强度结果基本一致,误差也几乎可以忽略。同时对比图7和图9也可以发现,2种方法得出的磁场分布趋势也是一致的。

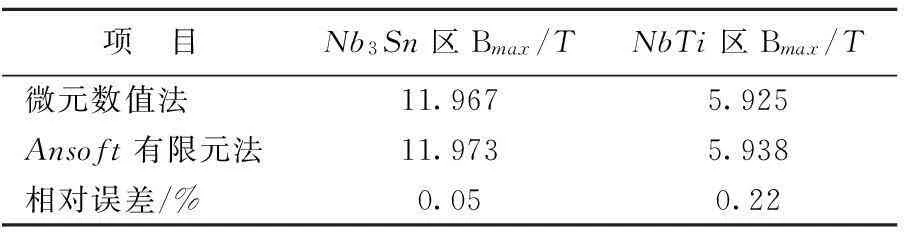
表2　计算结果

5结论

采用微元法计算CS模型线圈磁场分布是可行的,相比于Ansoft有限元法,具有很高的可修改性,在设计修改过程中,只需要根据需要分别修改2层线圈的层数、匝数和内外半径即可,同时该方法具有很快的运行速度,只需要约20s即可得出Nb3Sn、NbTi线圈的最大磁场及其分布;而后者则需要重新建立模型、加载、划分网格等,比较繁琐而且耗时较长。

电磁载荷的给出为线圈磁体的机械稳定性设计提供了参考,可防止局部应力集中导致的临界电流密度退化和过大应变导致的磁体失超。

[参考文献]

[1]SongYT，WuST，LiJG，etal.ConceptdesignofCFETRtokamakmachine[J].IEEETransactionsonPlasmaScience，2014，42(3):503-509.

[2]王秋良.高磁场超导磁体科学[M].北京:科学出版社,2007:13-16.

[3]ZhengJX，SongYT，LiuXF，etal.ConceptdesignofhybridsuperconductingmagnetforCFETRtokamakreactor[C]//FusionEngineering，2013IEEE25thSymposiumon，2013:1-6.

[4]CiazynskiD.ReviewofNb3Sn conductors for ITER[J].Fusion Engineering and Design，2007，82(5-14):488-497.

[5]ITEROrganization.ITER-D-2NHKHH v1.5[R].ITER Organization,2009.

[6]叶齐政,孙敏.电磁场[M].武汉:华中科技大学出版社,2008: 117-119.

[7]刘旭峰,杜世俊,叶民友.聚变堆用Nb3Sn超导磁体设计分析[J].合肥工业大学学报:自然科学版,2011,34(8):1183-1187.

[8]杜军.Nb3Sn超导磁体电磁分析[D].合肥:合肥工业大学,2012.

[9]赵博,张洪亮.Ansoft12 在工程电磁场中的应用[M].北京:中国水利水电出版社,2010:56-57.

(责任编辑何晓雄)