基于KHM的多层采样粒子滤波算法

基于KHM的多层采样粒子滤波算法

李菊1,2,余烨1,戴欢2,李克清2,夏瑜2,曹明伟1

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230009; 2.常熟理工学院 计算机科学与工程学院,江苏 常熟215500)

摘要:文章通过多层采样方式,将样本空间划分为多个部分,集中采样点到使概率密度函数值大的地方,大大减小了采样误差;在重采样阶段嵌入KHM聚类算法,通过将空间特征与权重分布近似的粒子进行聚类,降低总的样本数,提高了计算效率。样本经聚类处理后,在保持粒子状态后验分布的几何特征的同时,状态空间中的粒子数明显降低,计算效率显著提高。

关键词:多层采样;聚类;粒子滤波;重采样;运动目标跟踪

收稿日期：2014-06-04；修回日期：2014-10-27

基金项目：国家自然科学基金资助项目(61300186);高等学校博士学科点专项科研基金资助项目(20120111110003);江苏省自然科学基金资助项目(BK20140419);江苏省高校自然科学研究资助项目(14KJB520001;13KJB510001)；苏州市重点实验室资助项目(SZS201407)和常熟市社区资助项目(CS201404)

作者简介：李菊(1981-),女,江苏常熟人,合肥工业大学博士生,常熟理工学院讲师.

doi:10.3969/j.issn.1003-5060.2015.06.009

中图分类号:TP391. 4文献标识码：A

收稿日期：2014-06-04；修回日期：2014-10-15

Stratified sampling particle filter algorithm based on KHM

LI Ju1，2,YU Ye1,DAI Huan2,LI Ke-qing2,XIA Yu2,CAO Ming-wei1

(1.School of Computer and Information, Hefei University of Technology, Hefei 230009, China; 2.School of Computer Science and Engineering, Changshu Institute of Technology, Changshu 215500, China)

Abstract:In this paper, by using the stratified sampling method, the sample space is divided into multiple parts, grouping sampling points to the part of high probability density function value, so the sampling error is greatly reduced. In the resampling phase, the KHM clustering algorithm is embedded, the particles with approximate spatial characteristics and weight distribution are clustered, thus reducing the total number of samples and improving the computing efficiency. After the clustering, the geometrical characteristics of particles state posterior distribution is maintained, while the number of particles in the state space is significantly reduced and the computing efficiency is improved.

Key words:stratified sampling; clustering; particle filter; resampling; moving object tracking

粒子滤波作为一种新的滤波算法,是从20世纪90年代中后期发展起来的,有效地克服了扩展卡尔曼滤波的缺点。但粒子滤波自身也有一些弱点,会导致样本贫化现象[1-5],文献[6]将微粒群算法引入粒子滤波,采用微粒群优化方式,使粒子集向后验概率密度值较大的方向移动,很好地克服了样本贫化问题;文献[7]将优化组合引入粒子滤波,对被选取粒子和被抛弃粒子进行适当线性组合获取新的粒子,粒子多样性被大大增加,粒子滤波的估计精度也有很大的提高。针对计算量较大[8-12]的问题,文献[13]指出当使用适当的重采样方法时粒子滤波的计算复杂度为O(N)(N为粒子数目)；文献[14]引入粒子滤波的并行结构算法并进行了在线实时应用。对于一些状态空间模型中的线性组成部分,可以通过解析的最优滤波方法获取其状态向量的一部分。各种方法都在一定程度上缓解了样本贫化现象,降低了计算复杂度,但总的来说,并未从根本上解决这个问题。

本文通过多层采样的方式,把样本空间划分为多个部分,集中采样点到使概率密度函数值大的地方,采样误差大大减小。在重采样阶段嵌入KHM聚类算法,通过将空间特征与权重分布近似的粒子进行聚类,总的样本数被降低,提高了计算效率。样本经聚类处理后,在保持状态后验分布的几何特征的同时,状态空间中的粒子数明显降低,计算效率显著提高。本文提出的改进算法可以用到对实时性要求高的场合，通过设定合理的阈值(聚类半径)也可以自适应调节粒子数。

1粒子滤波算法原理

粒子滤波的基本原理[15]如图1所示,是采用随机样本描述概率分布,对采样粒子的位置和权重进行调整,对实际的概率分布进行近似,并用样本均值作为估计值,克服了扩展卡尔曼滤波器的缺点。

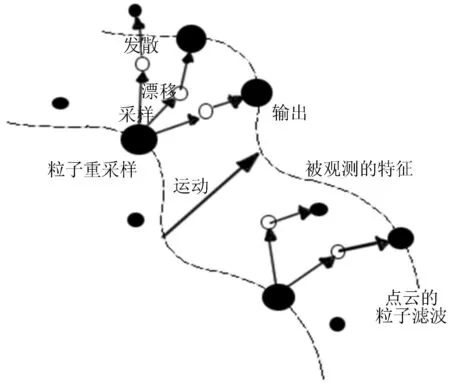
图1　粒子滤波算法原理图

2基于KHM的多层采样粒子滤波算法

2.1　多层采样

传统的粒子滤波算法从一个方向进行采样,造成粒子一般比较单一。而多层采样从多方向、多角度进行采样,采样误差被大大降低了。通过多层采样,把采样空间划分为多个子空间,子空间被称为层,这些不同的分层都具有相同的特性,在每一层中进行采样,每一层的概率密度函数为pi(x),那么p(x)用(1)式表示:

(1)

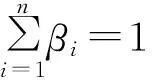
2.2　K调和均值聚类

假设降低采样密集度,会造成降低目标估计的准确性。所以,本文在粒子重采样时引入K调和均值聚类,利用权重进行粒子分配,既可以维持高采样率又可大大减少计算量,KHM算法的关键是运用了调和平均值这个概念,P个数a1,a2,…,aP的调合平均值HA的定义如下:

(2)

该函数有一特点,假如a1,a2,…,aP中任何一个元素小时,调和均值也会很小。如果元素中没有很小的值,调和均值就会很大。它就像是一个赋予每个元素一些权重的极小化函数k调和均值中,对于任意点而言,目标函数都计算了该点到所有中心的距离。当该点离很多中心点都非常接近时,该算法会将这些多余的中心转移到那些没有最近中心点的区域,这样获得的目标函数的值就会较小。研究中心迭代公式发现整个数据集中的成员都会对每个类的中心迭代产生影响,所以不论初始点取何值,都不会对中心的迭代产生很大影响。

2.3　算法整体思路

通过多层采样的方式,样本空间被划分为多个子空间,采样点被集中到使概率密度函数值大的地方,大大降低了采样误差,提高了精度。在重采样阶段嵌入KHM聚类算法,利用权重进行粒子分配,提高了粒子的利用率,算法的复杂度大幅度降低。同时因为嵌入了KHM聚类算法,保持了目标的分布特征。算法流程如图2所示。

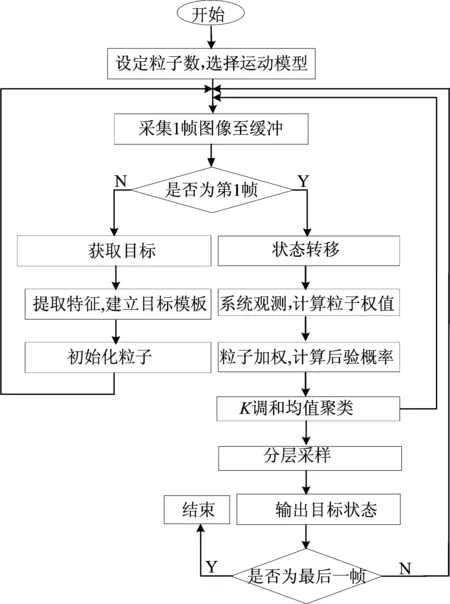
图2　算法流程图

2.4　算法基本步骤

2.4.1　初始化

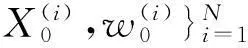
2.4.2　重要性采样

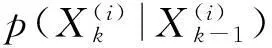
(2) 评估新的权重。

(3)

(3) 归一化权重。

(4)

2.4.3　输出

(5)

其中δ(·)是狄克拉函数。

2.4.4　重采样

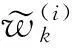
(1) 从数据集K中,随机抽取N个对象作为初始聚类中心K1,K2,K3，…，KN。

(2) 不断地使用聚类中心进行迭代计算,公式如下:

(6)

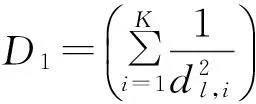
(3) 直到评价函数(7)式开始收敛，即

(7)

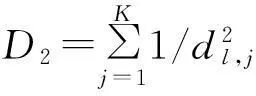
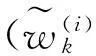
(8)

2.4.5　多层采样运用

对粒子集合进行更新，将多层采样运用于(8)式，则有：

(9)

2.4.6　结果输出

3仿真结果及性能分析

3.1　图像理解和运动目标跟踪

为了验证算法的正确性,研究在局部扰动背景情况下和目标形状发生变化时,改进算法的适应能力。

动态背景中的运动目标跟踪如图3所示。

图3　动态背景中的运动目标跟踪

分别对图3所示的局部扰动背景情况下目标姿态发生变化的动态序列做实验。VC++2010 和Open CV 编程实现,实现环境为1.6 GHz CPU,内存6.0 GB。

本文中选择了第2、13、16、30、114、132、166、236帧的实验结果,一方面,环境光照比较昏暗,光照在随时间发生变化,另一方面局部扰动背景是本图像序列的难点,对图3跟踪结果进行研究发现,本文算法在这2种情况下的跟踪效果较好,体现了较好的稳定性。此外，通过观察图3发现,运动目标姿态发生了很大的变化,该改进算法依然能进行稳定的跟踪。

3.2　比较实验

为了验证改进算法的有效性,对hall图像序列进行实验,将Mean Shift跟踪算法、传统粒子跟踪算法与改进的算法进行比较,实验结果主要从鲁棒性以及时效性进行分析。通过对粒子滤波中粒子权重的调整,很好地跟踪到目标。

图4所示为采用Mean Shift算法的跟踪效果图,Mean Shift算法计算量较小,框选已知的区域,目标跟踪实时较好,但模板更新能力较差,要想保持好的跟踪效果,在跟踪过程中必须保持窗口宽度不变。一旦目标尺度发生变化,跟踪就会失败。

图5所示为采用粒子滤波算法的跟踪效果图,粒子滤波算法用随机样本来描述概率分布,通过对采样粒子的位置和权重进行调整,来近似实际的概率分布,估计值采用了样本均值,但本身也具有计算量大的弱点,实时性较差。图6所示为采用本文改进算法的跟踪效果图,改进算法的复杂度大幅度降低,适用实时性要求高的场合。

为了比较改进粒子滤波算法和传统的粒子滤波算法的性能,本文分别对2种算法做了80次独立实验,结果见表1所列,改进算法的差错率更低,执行时间更短，大大提高了跟踪算法的稳健性、准确性和实时性。

图4　Mean Shift跟踪算法跟踪效果图

图5　粒子滤波跟踪算法跟踪效果图

图6　改进的粒子滤波算法跟踪效果图

项 目改进粒子滤波算法传统粒子滤波算法粒子数600600差错率1.11.4执行时间/ms2478

4结束语

本文通过多层采样的方式,把样本空间划分为多个部分,集中采样点到使概率密度函数值大的地方,减小了采样误差,只有传统算法的1/2。在重采样阶段嵌入KHM聚类算法,利用权重进行粒子分配,保持了粒子多样性,提高了粒子的利用率和实际应用中的计算效率。本文提出的改进算法可以用于对精度要求高与实时性要求高的场合。

[参考文献]

[1]蒋建国,李明,齐美彬.基于TMS320DM6437的运动目标实时检测与跟踪[J].合肥工业大学学报:自然科学版,2011,34(7):1007-1010,1023.

[2]Kwok C,Fox D,Meila M.Adaptive real-time particle filter for robot localization[C]//Proceedings of IEEE International Conference on Robotics and Automation,Vol 2,2003:2836-2841.

[3]Li P,Zhang T.Visual contour tracking based on particle filters[C]//Proceedings of Generative Model Based Vision, Copenhagen, 2002:61-70.

[4]Shan C,Wei Y,Tan T,et al.Real time hand tracking by combining particle filtering and mean shift[C]//Proceedings of Automatic Face and Gesture Recognition, 2004:669-674.

[5]Hue C,Cadre J L,Perez P.A particle filter to track multiple objects[C]//IEEE Workshop on Multi-Object Tracking, 2001:61-68.

[6]Hu W M, Tan T N, Wang L, et al. A survey on visual surveillance of object motion and behaviors[J].IEEE Transactions on Systems, Man, and Cybernetics-Part C: Applications and Reviews, 2004,34(3): 334-352.

[7]Paragios N, Deriche R. Geodesic active contours and level set for the detection and tracking of moving objects[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(3):266-280.

[8]李安平.复杂环境下的视频目标跟踪算法研究[D].上海：上海交通大学,2006.

[9]Doucet A,Godsill S J,Andrieu C.On sequential simulationbased methods for Bayesian filtering[J].Statist Comput,2000,10(3):197-208.

[10]Doucet A,Gordon N J,Krishnamurthy V.Particle filters for state estimation of jump Markov linear systems[J].IEEE Trans Signal Processing,2001,49:613-624.

[11]Gordon N J.A hybrid bootstrap filter for target tracking in clutter[J].IEEE Trans Aerosp Electron Syst,1997,33:353-358.

[12]Thrun S,Fox D,Dellaert F,et al.Particle filters for mobile robot localization[M]//Doucet A, de Freitas N,Gordon N.Sequential Monte Carlo Methods in Practice,Eds. New York: Springer-Verlag, 2001.

[13]Kashef B G,Sawchuk A A. A survey of new techniques for image registration and mapping[C]//Proceedings of the SPIE 0432: Applications of Digital Image Processing Ⅵ,1983:222-239.

[14]Anders E N. A constrained extended Kalman Filter for target tracking [C]//Proceedings of the IEEE International Conference of Radar, Philadelphia, USA,2004:123-127.

[15]Cho J U,Jin S H,Pham X D,et al.A real-time object tracking system using a particle filter[C]//International Conference on Intelligent Robots and Systems, 2006:2822-2827.

(责任编辑马国锋)