浅谈操作、体验等学习活动在数学几何教学中的作用
文/鲁锁志
浅谈操作、体验等学习活动在数学几何教学中的作用
文/鲁锁志
摘要:转变学习方式要求教师建立全新的学习活动理念,以学生为本,根据学生心理发展的特点,为学生创设实践活动和探索的情景,让学生在兴趣盎然、充满自信的活动状态中掌握数学知识,发展能力。学生正处于由直观形象思维向抽象逻辑思维过渡的阶段,动手操作活动把数学问题生活化,在几何教学中,让学生在操作活动中感知概念,在观察中”发现——猜想”,正确处理好“合情推理”与“演绎推理”的关系,加强“体验性学习”,有利于学生个性化的发展,积累丰富的数学活动经验,发展了学生的探究意识和实践能力。只有学生自觉投入学习,亲自体验求知的快乐,才能真正激发其学习兴趣;形成科学的态度,培养良好的学习习惯。
关键词:操作;体验;活动;探究式学习
中图分类号:G623
文献标志码:码:A
文章编号:号:2095-9214(2015)11-0038-02
新课改倡导自主、合作、探究的学习方式,使课堂教学发生了巨大的转变,但这种收效甚微的花样翻新课堂教学也引起了人们的质疑和反思:自主、合作、探究是具体的学习活动形式吗?,转变学习方式就是简单化的放任自学吗?学校教育背景下学生面对大量系统的课程目标和内容,单靠学生自发的阅读教材、解答问题就能达到三维目标吗?…学生学习是一项专门化的活动,有其内在的心理学规律,只有在科学设计的学习活动中,经过长期的学习实践,学生才能循序渐进地积累知识经验、发展能力,才能掌握学习方法,学会学习。因此,转变学习方式要求教师建立全新的学习活动理念,以学生为本,根据学生心理发展的特点,为学生创设实践活动和探索的情景,让学生在兴趣盎然、充满自信的活动状态中掌握数学知识,体验求知的快乐。
学生成为学习主体的重要标志是:他们积极参与各种教学活动,即积极参与观察、操作、实验、讨论、交流等活动;积极参与探究活动,通过对现象的分析、比较、运用归纳或类比等方法,不断发现问题、提出问题;积极开展思维活动,对自己和他人的意见进行质疑、反思,不断地分析问题、解决问题。为此,教师应把操作活动作为学生成为主体的一种重要的学习活动。
一、操作
“纸上得来终觉浅,绝知此事要躬行。”空洞抽象的讲解,使人感到枯燥乏味,而一次成功的实践活动将使人终生难忘。学习活动是学生相对独立的主体活动过程,是一个连续性、系列化的活动过程,是学生内部心理活动与外部行为相结合的过程。学生正处于由直观形象思维向抽象逻辑思维过渡的阶段,动手操作活动把数学问题生活化,启迪学生直观感知知识,发展思维,对理解和掌握知识起到至关重要的作用,是学习的重要方式。
(一)在操作活动中感知概念
新的课程标准着重强调教学要以学生为本,要培养学生学会学习的能力,这就要求我们在教学中充分给予学生自主的学习权力,避免出现:怕充分给予学生自主,就完不成教学任务;或不知如何给予学生自主,学生在课堂中没有自我意识,完全处于被动的接受状态这两种极端现象。有效的数学学习过程不能单纯地依赖模仿与记忆,教师应引导学生主动地从事观察、实验、猜测、验证、推理与交流等数学活动,从而使学生形成自己对数学知识的理解和有效的学习策略。要在教学中唤醒学生的自我意识,教师备课时应想学生之所想,在教学中应运用多种策略,给予学生自主学习的机会,在操作活动中提高学生自主学习的能力。我在讲解余角和(邻)补角的概念时设计了如下操作:学生在白纸上画一个直角或一个平角,然后在直角或平角内任画一条直线,观察着两个角有什么关系?并量一量这两个角的度数?通过实践操作学生获得了感性认识,从而进一步理解并掌握了概念。对于每一个新概念、新命题,教师应给学生提供充分的直观感知空间,让他们动手操作和观察猜想,如“三角形内角和定理”的证明,用剪纸拼接实验说明,同学们在实验、观察中获得了添加辅助平行线的方法,这样,把三角形三个内角转化为平角或两平行线间的同旁内角,即把新知转换为旧知,既符合学生认知特点,又丰富了学生感性经验,从而获得理性论证的基础。在讲“角、角、边”判定定理时,我又设计了如下活动:让学生画两角一对边(40度、60度、3厘米)的三角形,结果有同学发现所画三角形并非都全等,从而加深了对“等角的对边对应相等”这一句话的理解。学生在亲历“做数学”的过程中易于发现并理解图形的概念、性质内涵,便于掌握数学知识技能和思想方法,同时获得广泛的数学活动经验。
(二)在观察中”发现——猜想”
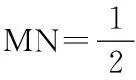
图1
(三)在归纳中“演绎推理”
长期以来,中学数学十分强调逻辑推理的严谨性而忽视了生动活泼的合情推理,使人们认为数学就是一门纯粹的演绎科学,事实上数学史每一个重要发现都离不开“合情推理”与“演绎推理”,合情推理实质是“发现——猜想”,这有助于探索解决问题的思路、发现结论,演绎推理用于证明结论的正确性。当前教材弱化了几何证明繁杂程度,突出对证明意义的理解,要求通过观察、归纳、类比等活动获得数学猜想,并寻求证明猜想的合理性,这是一大进步。通过猜想得出结论的例子也是非常多的,如很多的探究规律性的问题。n边形的内角和、正多边形对称轴的条数等都可以通过归纳或推理得出。但仅有猜想是不够的,有些命题通过有限次实验或观察不一定正确,只有通过严格的“演绎推理”得到正确的结论。如在对“任一四边形中点连线所得四边形形状”的猜想过程中,只有通过证明才能实现对所有情形的验证,从而让学生进一步体会证明的必要性;“合情推理”与“演绎推理”有机结合、相得益彰;只有处理好“合情推理”与“演绎推理”的关系,才有利于进一步提高学生的逻辑思维能力。
学生是数学学习的主体,在积极参与学习活动的过程中不断得到发展。学生获得知识,必须建立在自己思考的基础上,思考能力的培养可以通过接受学习的方式,也可以通过自主探索等方式;学生应用知识并逐步形成技能,离不开自己的实践;学生在获得知识技能的过程中,只有亲身参与教师精心设计的教学活动,才能在数学思考、问题解决和情感态度方面得到发展。为此,在教学中,教师应成为学生体验学习活动的组织者、引导者、合作者,为学生的体验式学习发展提供良好的环境和条件。
二、体验
我听了“游泳技巧”,很快就忘记了;我“观摩游泳”,很快就领会了;我“下水游泳”,才深刻理解了。这句话表明了亲身经历的重要性。基础教育课程改革目标指出:“改变课程过于注重知识传授的影响,强调形成主动的学习态度,使获得基础知识与基本技能的过程同时成为学会学习和形成正确价值观的过程;加强课程内容与学生生活以及现代社会科技发展的联系,关注学生的学习兴趣和经验……”,将“体验性学习”提到了十分突出的位置,这是对既往“接受性学习”的重大突破,是一种符合时代精神和当代青少年身心发展特点的学习方式。这种学习方式具有主动性、实践性、过程性等特点,它以科学知识为探究对象,以科学探究为体验载体,让学生自由开放地感知学习材料,在活动情景构建知识,形成个性化的认识;这种探究式学习方式,体现了“以人为本”的原则,这就要求我们教师在课堂上应充分调动学生生的眼、手、口、脑等多种感官,诱发学生产生自我实现需求的创造性思维的时间和空间,根据学生的年龄特点,身心发展的规律以及数学活动自身的特点,让学生参与体验一些具有思考性、探索性、思想性、趣味性或能引起认知冲突的问题情境,以激发求知欲望,自主地发现问题和解决问题。
在探索勾股定理的教学中,我特别强调探求新知的经历和获得新知的体验,注重创设问题情境让学生经历探索勾股定理的学习过程:①创设情境,欣赏2002年世界数学家大会会标;②自主探索,拼图验证勾股定理:利用4个全等的直角三角形,设法拼出一个含有斜边c为边长的正方形,突出大正方形边长为a+b;或拼出“弦图”(中间缺一个边长为a-b的小正方形),验证勾股定理。③情景体验:毕达哥拉斯正坐在客厅品茶,一不小心推倒了一个火柴盒,就在这一瞬间,他发现了一个事实,如图(3),你能说出这个事实,并验证吗?④活动延伸:如图(4)你能在L形图(两个大小不一的正方形拼成)中剪2刀,拼出一个正方形,并能验证勾股定理吗?数形结合,学生表现出浓厚的兴趣,在活动中获得了对勾股定理的深刻认识,积累了丰富的数学活动经验,发展了学生的探究意识和实践能力。人的创新意识只有活跃在形成结论成果的探索过程中,才能释放创造潜能,发现真理。
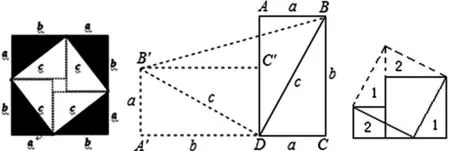
图2 图3 图4
数学教学是数学活动的教学,是师生交往、互动与共同发展的过程。学生是学习的主人,“我们用不着劝说一只鸟儿去飞,樊笼打开之后它立刻就会飞的”,我们的课堂教学应该广泛利用各种课程资源,借助开放、互助的教学手段与多媒体平台,激发学生探究数学的热情;学生只有通过自己的探索才能体会到学数学和做数学的乐趣;学生在体验数学和做数学过程中,教师应从学生的生活生活经验出发,通过生动有趣的教学情境充分发挥学生的动手操作能力和自主创造能力,让学生在体验学习中扮演主动角色;通过课堂教学的师生互动,把“静态的知识”变为“动态的活动过程”,促进学生自主学习,形成探究能力,共同创设出新的生命特质。
(作者单位:郎溪县第二中学)
参考文献:
[1]倪牟双,邵志豪.《学习方式与学习活动设计》.天津教育出版社,2013年第1版.
[2]《课堂教学问题诊断与解决》初中数学,盛建武.天津教育出版社,2009年第1版.

