欣赏数学之美
文/黄振
摘 要:数学不但对社会的进步提供的动力,数学的美还给以人们享受。数学美不但有多种表现形式,如简洁美、对称美、统一美等。数学美具有一定的价值,欣赏数字之美对调动学生积极性,培养学生的应用和创新意识,提高学生素养,塑造学生的数学观具有重要作用。
关键词:简洁美;对称美;统一美;形式美;隐藏美
欣赏数学之美
文/黄振

摘要:数学不但对社会的进步提供的动力,数学的美还给以人们享受。数学美不但有多种表现形式,如简洁美、对称美、统一美等。数学美具有一定的价值,欣赏数字之美对调动学生积极性,培养学生的应用和创新意识,提高学生素养,塑造学生的数学观具有重要作用。
关键词:简洁美;对称美;统一美;形式美;隐藏美
作者简介:黄振,研究生,福建省漳州市芗城区闽南师范大学数学与统计学院。
中图分类号:G427
文献标志码:码:A
文章编号:号:2095-9214(2015)11-0117-02
数学是利用符号语言研究数量、结构、变化以及空间模型等概念的一门学科。数学,作为人类思维的表达形式,反映了人们积极进取的意志、缜密周详的逻辑推理及对完美境界的追求。
一、美与数学美的含义
美在哲学中定义为:美是具体事物的组成部分,是具体环境、现象、事情、行为、物体对人类的生存发展具有的特殊性能、正面意义和正价值,是人们在密切接触具体事物。受气刺激和影响产生了愉悦和满足的美好感觉后,从具体事物中分解和抽取出来的有别于丑的相对抽象事物和元实体。[1]
那数学美又是什么呢?数学思想大师罗素就曾这样毫不掩饰地说过:“数学,如果正确地看它,则具有……至高无上的美,正像雕刻的美,是一种冷而严肃的美,这种美不是投合我们天性的微弱的方面,这种美没有绘画或音乐的那些华丽的装饰,它可以纯净到崇高的地步,能够达到严格的只有最伟大的艺术才能显示的那种完美的境地。一种真实的喜悦的精神,一种精神上的亢奋,一种觉得高于人的意识,这些是至善至美的标准,能够在诗里得到,也能够在数学里得到。”[2]
二、数学美的表现
数学美的表现形式是多种多样的,关键是看你从何种角度去体会,去欣赏。就像一千个人眼里有一千个哈姆雷特一样,每个人对数学美都有不同感受。数学从分支上看有几何美、代数美、概率美等;从思想方法上看有抽象美、演绎美、划归美、类比美等;从一般美学上看有简洁美、对称美、统一美、形式美、隐藏美等等。这里主要谈谈数学的简洁美、对称美、统一美、形式美、隐藏美:
(一)简洁美
简洁的事物总是蕴藏着美的真谛,化繁为简本就是一种高超的本领。数学是一门追求简洁的学科,简洁性是数学的一个显著特征,反映的是数学的简洁美。伟大的物理学家爱因斯坦曾经说过:“美,本质上终究是其简单性。”
著名而且使用非常广泛的勾股定理是数学简洁美的又一典范,直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。
(二)对称美
对称是现实世界非常常见的一个美学性质,没有对称性的世界是无序的、杂乱无章的,没有对称性的东西是孤寂的、呆板的,不具体有生命力。所以,对称美是我们生活中经常追求的一种美,比如对联的对称美、建筑物的对称美等。
其实,数学中也蕴含着对称美。例如,在高等代数中,n阶行列式把n·n个元素按n行n列排成一个正方形,这使人感到整齐和对称。[3]数学的对称美更多体现在图形的对称性上。从平面到立体,无不体现着数学的对称美。
(三)统一美
统一性又可作同一性,追求同一性又是数学的一个基本特征。统一性是指部分与部分、部分与整体之间的内在联系或共同规律所呈现出来的和谐一致[4]。数学的发展是逐步统一的过程。希而伯特曾说统一的目的就是:“追求更有力的工具和更简单的方法”。
从相同几个数的连加到乘法,从相同几个数的连乘到幂的运算,这都体现的数学的统一发展规律,也体现的数学的统一美。所有与角α终边相同的角,连同角α在内,可构成一个集合:S={β/β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和,这就将任一与角α终边相同的角统一起来了,这还包括正角与负角的统一。
(四)形式美
我国古代的数学可以说是星光璀璨,如数学家杨辉发现的杨辉三角,杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
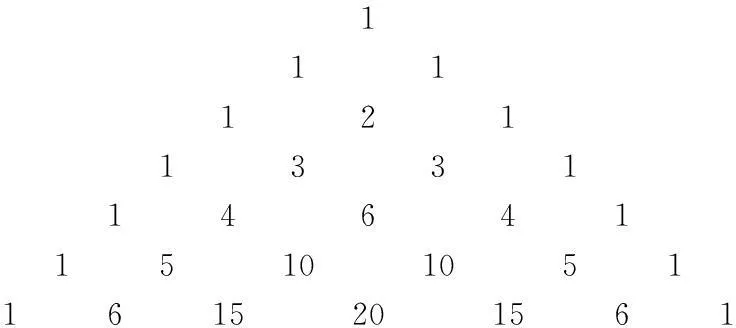
杨辉三角最本质的特征是,它的两条斜边都是由数字1组成的,而其余的数则是等于它肩上的两个数之和。自上而下,从左往右,杨辉三角无不体现着数学的形式美。
再来看看下面的两组式子:
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
123456×9+7=1111111
1234567×9+8=11111111
12345678×9+9=111111111
123456789×9+10=1111111111
1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111=123454321
111111×111111=12345654321
1111111×1111111=1234567654321
11111111×11111111=123456787654321
111111111×111111111=12345678987654321
两组式子是数字0、1、2、3、4、5、6、7、8、9通过运算符的简单组合,但是其形式上美,让人看了觉得是一种享受。如第二组的每一个等式左边是两个相同的由1组成的数,右边的积则刚好是一个对称的数,如123454321,这样的形式难道不美吗?
(五)隐藏美
数学是一门抽象的学科,简单的符号语言或表达形式却不失深刻的内涵和意义。数学的美有时不是一眼就可以看出来了,它具有一定的隐藏性,需要我们进行深入的挖掘,细细的品味方能体会其中的美。
杨辉三角中就具有隐藏的数学美,如果我们将杨辉三角以下方式排列,那么自左下到右上对角方向上的数字之和分别是1、1、2、3、5、8、13、…,这组数刚好就是斐波那契数列,其中的每一个数都是斐波那契数,即:

斐波那契数列是一个有趣而神秘的数列,细心研究该数列,我们发现其背后隐藏着不少有趣的性质。例如,将该数列的每一项都平方得到一组数,然后将这组数的前n(n∈2,3,4…)项相加,得到的和是两个斐波那契数的乘积,即
1+1=2=2×1
1+1+4=6=2×3
1+1+4+9=15=3×5
1+1+4+9+25=40=5×8
1+1+4+9+25+64=104=8×13
……………………………………………
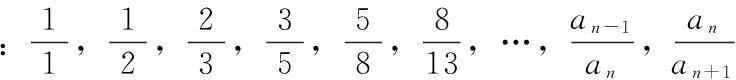
杨辉三角中竟然隐藏着斐波那契数列,而看似简单的斐波那契数列又蕴含着如此多的美,这正好说明数学的美是有隐藏性的,需要我们用心去挖掘、去发现,去品味
三、数学美的价值
数学能给予我们什么?美国著名的数学史家、数学教育家与应用数学家莫里斯·克莱因曾经说过一段话:“音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的一切”[5]。
在数学教学中,引导学生去挖掘和欣赏数学的美具有重要的作用:欣赏数学的美,可以激发学生的学习热情,调动学生的学习积极性;欣赏数学的美,可以锻炼学生的思维,培养学生的应用意识和创新意识;欣赏数学的美,可以陶冶情操,提升学生的数学修养和素质;欣赏数学的美,可以更好地塑造学生的数学观和学习观。
四、总结
总之,数学世界是有趣的、美妙的,并不是枯燥无味的,数学的美是生动的、活泼的、广泛的,它存在于我们生活的方方面面,只要我们怀着一颗虔诚的心和一双智慧的眼睛就能发现数学的美,就能欣赏数学的美,进而用数学的美给我们创作更多更好更高的价值,让数学之美为我们服务。
(作者单位:闽南师范大学数学与统计学院)
参考文献:
[1]陈浩.数学娱乐与数学教学[D],中国优秀硕士学位论文全文数据库社会科学2辑,2011(51).
[2]罗素.我的哲学发展[M].北京:商务印书馆,1982.
[3]张玉芳.浅谈数学之美[J],平原大学学报,1996(3):53~54.
[4]张小宁.浅谈数学之美[J],科技资讯,2007:178.
[5]曹鹏,符方健,黄婷,罗自强.浅析数学之美[J].教育教学论坛.2013(30):120~121.


