例谈数学模型思想在教学中的渗透

王立敏

摘 要：按课程标准的要求，数学教学就是要教给学生前人构建的数学模型和怎样构建模型的思想方法。通过建模教学，可以加深学生对数学知识和方法的理解和掌握，调整学生的知识结构，深化知识层次；同时，培养学生应用数学的意识和自主、合作、探索、创新的精神。

关键词：小学数学；建模教学；模型思想

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2015）20-0069-02

模型思想是《数学课程标准》（2011版）新增的10个核心概念之一，作为一线教师该怎样将这一重要的数学思想渗透于自己的日常教学之中呢？下面结合冀教版小学数学四年级下册“探索多边形中隐含的规律”一课，粗线地谈谈自己的一点做法。

一、抽象数学问题——建模起点

新课标指出，建模的首要环节是“从现实生活或具体情境中抽象出数学问题”。“抽象”是在认识事物的过程中舍弃其非本质属性，而取其本质属性。数学模型的抽象性、概括性都很强，任何一个数、一个公式、一个概念和规律都是抽象、概括的过程。在“探索多边形中隐含的规律”一课中，我是这样创设情境、抽象数学问题的。

师：谁知道我们学过哪些四边形？

生：长方形、正方形、平行四边形、梯形。

师：发现这些图形的共同的特点，或许你能明白这些图形为什么叫四边形？

生：它们都由四条边围成图形。

师：你能根据这几个图形边的数量给它们起名吗？课件出示四个多边形。

师：这些图形统称为多边形。今天，我们就一起探索多边形中隐含的规律。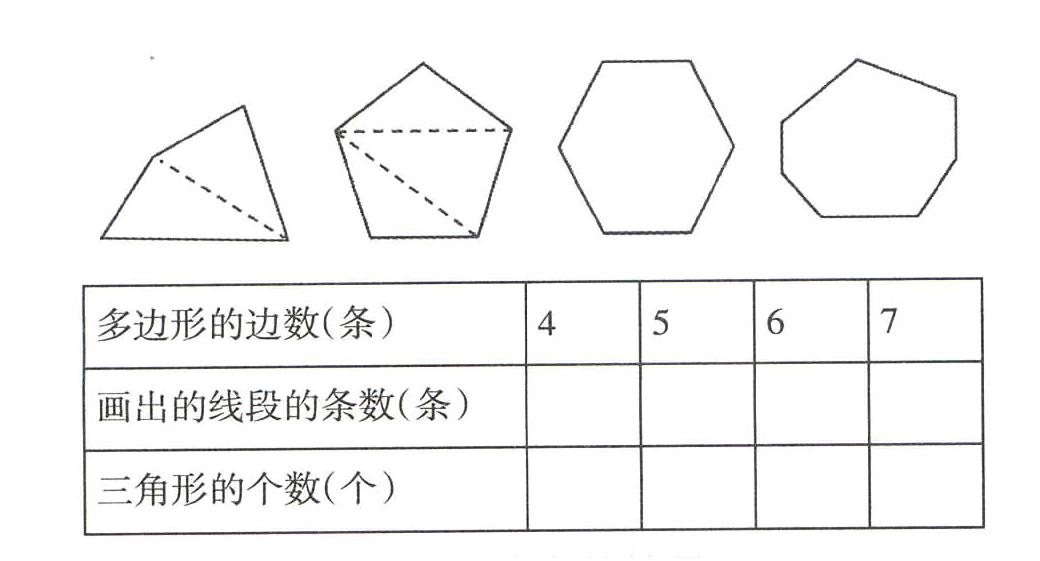

此环节，教师利用四边形的定义进行知识的迁移，使学生获得五边形、六边形、七边形等多边形的概念，从而引发学生对问题的探究——探索多边形中隐含的规律。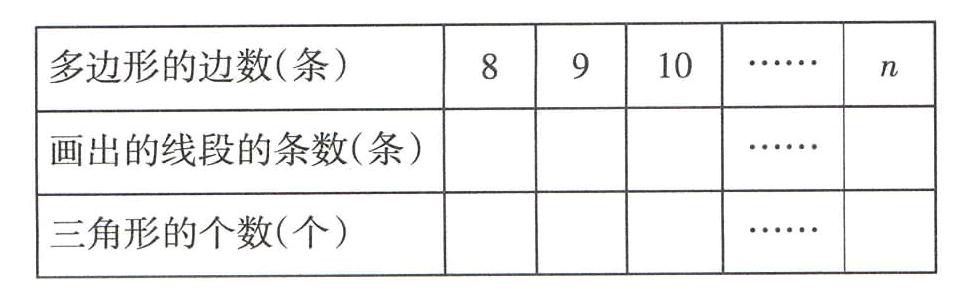

二、做中学——建立模型

动手操作是学生学习数学的重要途径和方法，它能把抽象的数学知识变得看得见、说得清，学生通过动手、动脑、动口参与学习过程，使操作、思维、语言等有机结合，从而建立清晰的数学模型。本节课，以让学生经历操作、感受规律为出发点，使学生在操作、观察、思考、列式的过程中感受多边形中隐含三角形的个数的规律及多边形的内角和规律。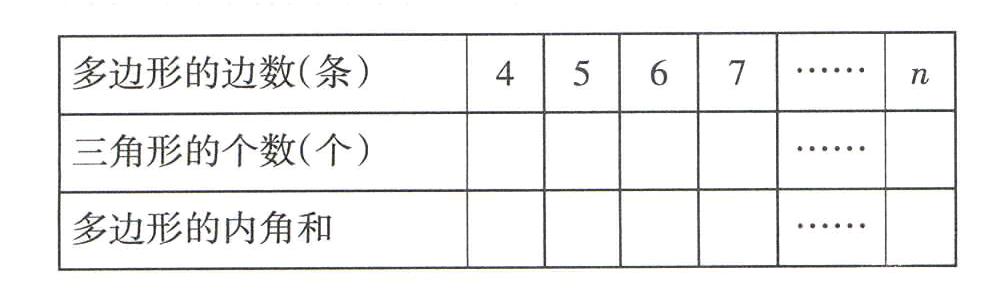

（一）探索四边形、五边形如何分割成三角形

1.师：认真观察四边形、五边形是怎样分割成三角形的，你能照样子画出虚线并填表吗？

学生交流画线和填表的结果。

师：观察表中的数据，发现了什么？

学生可能会发现：在四边形上画1条线段，分成2个三角形；在五边形上画2条线段，分割成3个三角形；在六边形上画3条线段，分割成4个三角形；在七边形上画4条线段，分割成5个三角形，一个比一个多画一条线段，就多分出一个三角形。

师生总结：

画线段的条数=多边形边数-3；

三角形个数=多边形边数-2；

画线段的条数=三角形的个数-1。

根据发现的规律填表

（二）探索多边形的内角和

师：前面我们学过三角形内角和是180°，那么四边形的内角和是多少度？说一说你是怎样想的？

生：四边形可以分成两个三角形，一个三角形的内角和是180°，两个三角形的内角和就是180°×2=360°

师：非常棒！看来你是利用前面我们刚刚发现的多边形中隐含三角形的个数的规律来做的。下面请同学们小组合作，完成下面的表格。

“智慧自动作发端”，学生在“照样子画出分割多边形成三角形”的活动中，不仅丰富了操作经验，而且通过观察、思考、交流等一系列过程实现了操作经验与思考经验、策略经验的有机融合，从而使学生积累了活动经验，找到多边形中隐含的规律，初步建立了数学模型。

三、思中学——应用模型

新课标指出，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。通过数学模型的应用，使学生体会数学的价值。

教学片断：

出示教材上的4幅图

师：我们再来看一道有关扣子的问题，观察扣子摆放的规律。请同学们自己完成表格。

要求学生自己完成后交流摆或画的图形。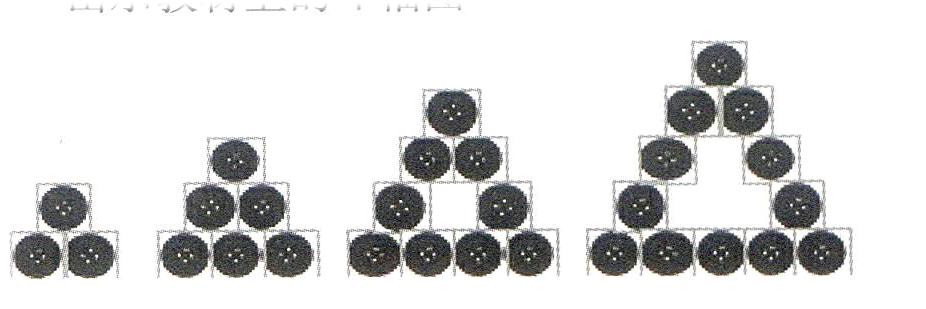

师：你发现了什么规律？用含有字母的式子表示出来。

以上教学片断，教材将学生生活中常见的扣子和三角形结合起来，使得教学内容变得生动、丰富，教学过程中让学生经历将生活问题抽象成数学模型并解释与应用的过程，使学生在数学思考中应用数学模型。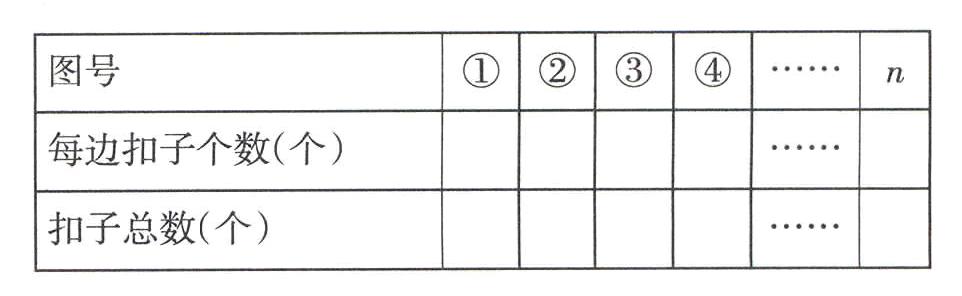

总之，模型思想的渗透，需要教师提供大量、丰富的感性材料，创设能够激起学生探索欲望的问题情境，让学生找到规律，积累感性经验，构建数学模型。同时还需对数学模型进行实践，让学生在逐步思考、运用中形成模型思想，提高学习数学的兴趣，培养创新意识。