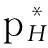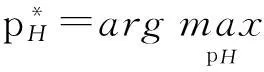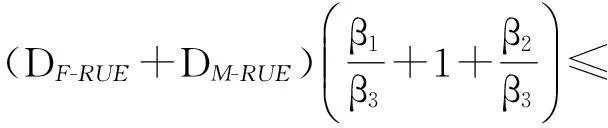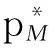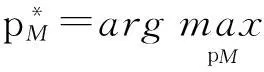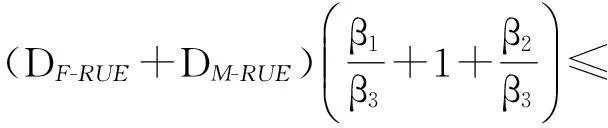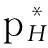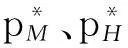基于Stackelberg博弈的最优频谱分配与定价策略

基于Stackelberg博弈的最优频谱分配与定价策略*

周雄冯穗力†

(华南理工大学 电子与信息学院， 广东 广州 510640)

摘要：针对家庭基站部署与运营，以及与宏基站共享频谱资源所面临的难题，提出了一种基于Stackelberg博弈的最优频谱分配与定价策略.通过建模基站与用户之间的博弈，分析了资源定价与用户需求的关系；通过建模宏基站与家庭基站之间的博弈，给出了多种场景下双层分级蜂窝网络的最优频谱分配与定价策略.该策略能按需地为宏基站与家庭基站分配频谱，最大化宏基站与家庭基站的频谱效益，并能有效地激励运营商与用户积极部署家庭基站，加速绿色通信网络的建设进程.

关键词：双层分级蜂窝网；Stackelberg博弈；频谱分配；频谱定价

中图分类号：TN929.5

doi：10.3969/j.issn.1000-565X.2015.03.014

文章编号：1000-565X(2015)03-0098-05

收稿日期：2014-09-23

基金项目：* 国家“863”计划项目( 2014AA032702);国家自然科学基金资助项目(61204087,51173049,61306099)；广州市珠江科技新星项目(2014J2200053)；华南理工大学中央高校基本科研业务费专项资金资助项目(2014ZM0003,2014ZZ0028)

作者简介：兰林锋 (1983-)，男，博士，副研究员，主要从事薄膜晶体管研究.E-mail: lanlinfeng@scut.edu.cn

随着用户对无线通信需求的不断提高，家庭基站在未来无线通信中将发挥重要作用[1].家庭基站通过缩短基站与用户之间的传播距离，提高了无线通信速率，改善了室内覆盖效率，保证了用户的服务质量.因此家庭基站技术受到了广泛的关注，运营商已经开始部署家庭基站.然而，家庭基站的推广，将面临两大难题：①家庭基站如何与宏基站共享有限的注册频谱资源；②如何选择部署与运营方式.

家庭基站与宏基站可以采用同频组网或异频组网方式共享频谱资源.文中主要研究异频组网场景.对于异频组网的频谱分配问题，目前的研究热点是，频谱已经定量分配给家庭基站和宏基站后，家庭基站网络如何合理地使用频谱资源，以提高频谱利用效率[2-5]，如家庭基站间的频谱冲突消除[2]、基于认知与博弈的频谱分配[3-4]、高能效的无线资源管理等[5].而如何最优地、定量地将频谱资源分配给宏基站与家庭基站，目前还鲜见相关研究报道.

家庭基站的部署主要有3种方式，即运营商部署、用户部署与联合部署[6].未来大多数家庭基站需要安装在用户私人住宅内，若由运营商安装，则会面临入场费昂贵、工作量巨大等困难，很难快速高效地完成部署工作；因此，家庭基站的广泛部署须有用户的积极参与.用户私人住宅内的家庭基站运营时，需要用户提供能耗与维护，若运营商独得家庭基站收入[7]，用户不仅对家庭基站的安装意愿较低，同时会自私地选择封闭用户组模式，从而降低了家庭基站的有效覆盖[8].因此，激励用户参与家庭基站部署，并开放家庭基站服务，是快速高效地完成家庭基站部署的重要前提.研究表明部署家庭基站能有效提高基站的整体收益[7]，部署家庭基站会为运营商带来更大效益，特别是宏基站频谱效率低下时，家庭基站带来的效益更加明显[9-10]；同时文献[11]指出经济回馈能够激励用户安装家庭基站并开放其服务，但是这些研究成果均没有给出具体的用户激励方案.因此，亟需可激励用户参与家庭基站部署与运营的收益分配方案.

综上所述，合理地为宏基站与家庭基站分配频谱带宽，并制定用户激励方案，有利于解决家庭基站的部署问题.宏观地看来，频谱资源的需求量与其定价密切相关.由于宏基站与家庭基站提供的服务质量不同，将导致这两种通信服务出现差异化的价格，用户对二者的服务需求也不相同.为按需地将频谱资源分配给宏基站与家庭基站，频谱资源的分配需要与其定价进行联合分析，文中采用Stackelberg博弈分析频谱定价与用户需求的关系，针对多种场景，为宏基站与家庭基站按需分配频谱资源，并进行差异化定价，最大化运营商以及家庭基站拥有者的频谱效益.

1系统模型

文中考虑由宏基站与家庭基站组成的双层分级蜂窝网络，宏基站由运营商部署，家庭基站由用户购买并部署，宏基站与家庭基站异频地共享有限的注册频谱资源.在本节中，将采用Stackelberg博弈建模宏基站与用户之间的博弈过程，以其作为后续分析的基础.Stackelberg博弈又称领导者-跟随者博弈，蜂窝网络中，基站首先决定其行动策略，用户跟随基站策略而行动，基站对频谱资源的定价与用户对频谱资源的购买过程可采用Stackelberg博弈建模，其具体过程为：第1步，基站制定带宽单价p，并将价格告知用户；第2步，用户根据p理性地购买带宽b.为不失一般性，文中讨论的频谱单价p为归一化价格，即p∈(0,1].根据文献[12]的用户通信效益模型，用户进行通信所得的收益为

G(c,b,p)=ln(1+cb)-pb

(1)

式中：c为归一化的用户当前频谱效率，可假定服从均匀分布[13]；p为频谱单价；b为用户占用的带宽.对于用户而言，将为最大化其收益而理性地决定带宽购买量b.通过式(1)可得，用户的最佳带宽需求量b*为

(2)

移动通信系统通常采用蜂窝小区技术，小区边缘的用户也能获得满意的频谱效率，因此，假定基站有效覆盖范围内，最小频谱效率为cmin.此时，基站覆盖范围内所有用户对基站服务的总带宽购买量为

(3)

式中a=max(cmin,p).为保证宏基站覆盖范围内用户能有效接入宏基站，由式(2)可知，须使cmin≥p.频谱资源充足时，基站利用频谱资源获得的总效益F(p)为

F(p)=D(p)p=1-cmin+plncmin

(4)

又因为有

(5)

即频谱总收益是cmin的减函数，因此，须适当设定蜂窝小区参数，使得cmin=p，从而最大化频谱总效益.令B为基站的总带宽，则实际获得的频谱总收益为

(6)

显然Bp是带宽单价p的增函数.而F(p)对p求导有

(7)

因此，F(p)是带宽单价p的减函数，若基站最大化其获得的总利益，最佳带宽单价p*与系统总带宽满足如下关系：

(8)

从上述分析可知，资源价格将影响用户需求，从而影响频谱总效益，最优的定价策略将带来最大化的频谱收益.下文将讨论部署家庭基站后，如何制定差异化的定价方案，并为家庭基站与宏基站分配带宽，促成双赢局面.

2频谱分配与定价策略

一般地，宏基站由运营商部署并维护，家庭基站由其所有者购买安装，并使用运营商的注册频谱资源.因此，假定运营商独得宏基站的频谱效益，并与家庭基站拥有者分享家庭基站的频谱效益.令宏基站带宽单价为pM，家庭基站带宽单价为pF，并且pF=pH+αpM.式中：pH为家庭基站拥有者的获利单价，αpM为运营商的获利单价，称α为利益保证系数.宏基站、家庭基站以及用户之间的博弈建模如图 1所示.基站与用户之间博弈时，基站建模为领导者，首先决定定价策略，用户作为跟随者，根据频谱价格决定带宽购买量.对于宏基站与家庭基站，宏基站建模为领导者，家庭基站建模为跟随者，同时在该过程中，通过对用户带宽需求的分析，按需地为宏基站与家庭基站分配频谱带宽.

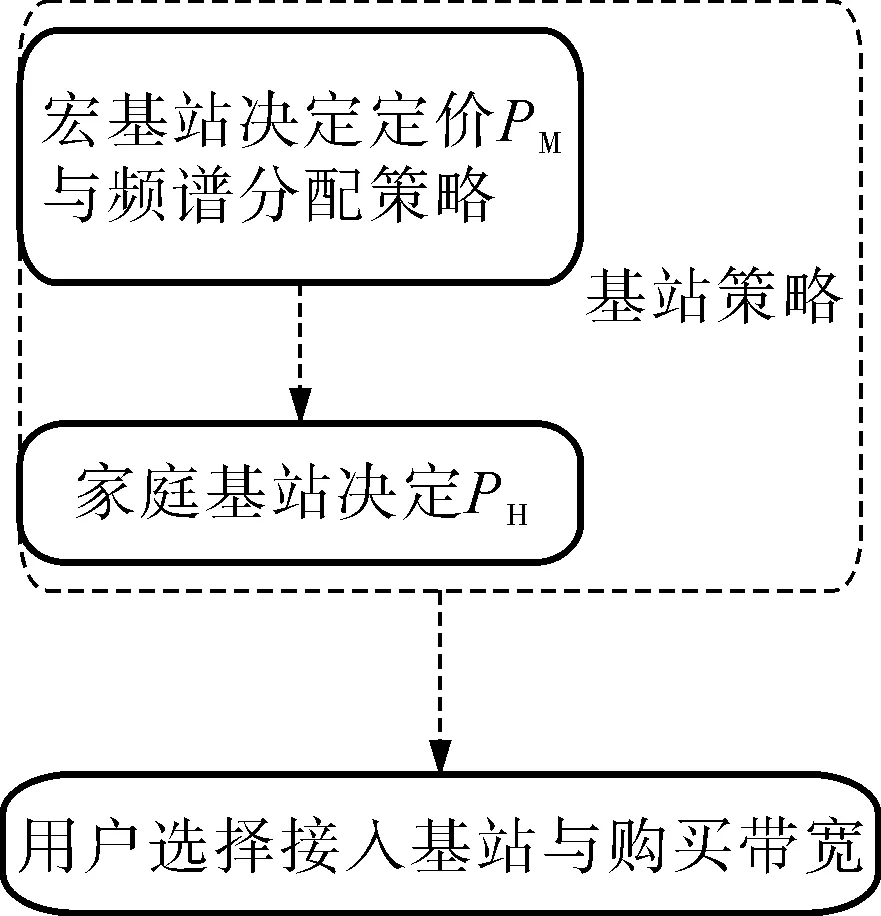
图1　三步Stackelberg博弈模型 Fig.1　Three-stage Stackelberg game model

2.1用户需求分析

在双层分级蜂窝网中，根据式(2)可知，若用户接入了宏基站，则其带宽购买量b*(pM)为

(9)

通常家庭基站的服务半径小，用户移动速度低，信道条件较好.因此，文中假定家庭基站归一化的频谱效率为1.此时，若用户接入了家庭基站，则其带宽购买量b*(pF)为

(10)

2.2针对理性用户的最佳策略

本节将针对理性用户，分析用户将会如何选择宏基站或家庭基站，定量地为宏基站与家庭基站分配带宽，并进行差异化定价.在双层分级蜂窝网中，理性用户会在家庭基站与宏基站之间选择该用户获利较大的基站.将式(9)代入式(1)可得，用户选择宏基站的获利为

(11)

同理，用户选择家庭基站的获利为

(12)

令f(c)为用户选择宏基站服务与家庭基站服务之间的获利差：

f(c)=G1(c,b*(pM),pM)-G0(1,b*(pF),pF)

(13)

显然，当且仅当f(c)>0时，将选择接入宏基站.通过f(c)对c求导有

(14)

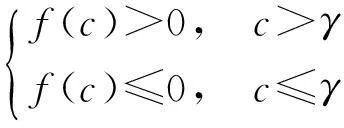
(15)

因此，用户将根据其所获得的宏基站频谱效率选择不同基站，并且γ是其选择的门限值.当pF≤pM时，γ≥1≥c，f(c)≤0成立，此时相比宏基站服务，家庭基站服务有更高的频谱效率，更低的单位带宽价格，用户只会选择接入家庭基站，造成宏基站网络资源的巨大浪费，这种情形在实际中出现的可能性较低.因此，文中只需讨论当pF>pM时，频谱资源的分配与定价策略.

当pF>pM时，与式(3)同理可得，理性用户对宏基站与家庭基站的带宽总需求DM与DF分别如式(16)、(17)所示.

(16)

(17)

此时，运营商与家庭基站拥有者获得的频谱效益GO与GH分别如式(18)、(19)所示.

GO=αpMDF+pMDM

(18)

GH=pHDF

(19)

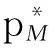
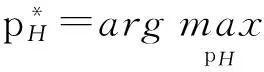
(20)

s.t.DF+DM≤B.

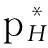
(21)

由上式可知，家庭基站拥有者的最佳定价策略是对运营商定价的跟随.宏基站带宽的最佳定价为

(22)

s.t.DF+DM≤B.

其中，约束条件为系统总带宽不小于用户的总购买量.虽然式(22)无法给出一个闭式解，但是频谱分配与定价方案是在网络运营前确定的，不需要进行实时计算，因此遍历法即可对其求解.当获得了最优资源定价解时，式(16)与式(17)分别为宏基站与家庭基站所需的最佳频谱带宽.

2.3存在有限理性用户时的最佳策略

一般地，只能有限达到理性行为的行为人，被称之为有限理性参与者[15].在本文中，若用户按照系统模型中获利最大原则，即按照式(15)理性地选择基站，并最大化式(1)所示用户效益，则为理性用户；而部分用户可能因客观条件限制无法接入到家庭基站，或者用户本身注重用户体验(如：考虑到移动终端的辐射及电池寿命等问题，只选择家庭基站服务)，不满足理性选择基站的原则，这些用户就定义为有限理性用户.之所以称为有限理性用户，是因为其在选择基站类型时，不满足完全理性的条件，而购买带宽时，依然按照该用户获利最大的原则决定带宽购买量.此时，双层分级网络中主要存在如下3类用户：

(1)既能够接入到宏基站，又能够接入到家庭基站的理性用户(RUE)，记为RUE.

(2)在家庭基站覆盖之外，只能接入宏基站的有限理性用户(BRUE)，记为M-BRUE.

(3)只接入家庭基站的有限理性用户，记为F-MRUE.

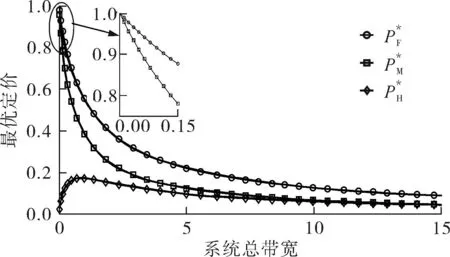
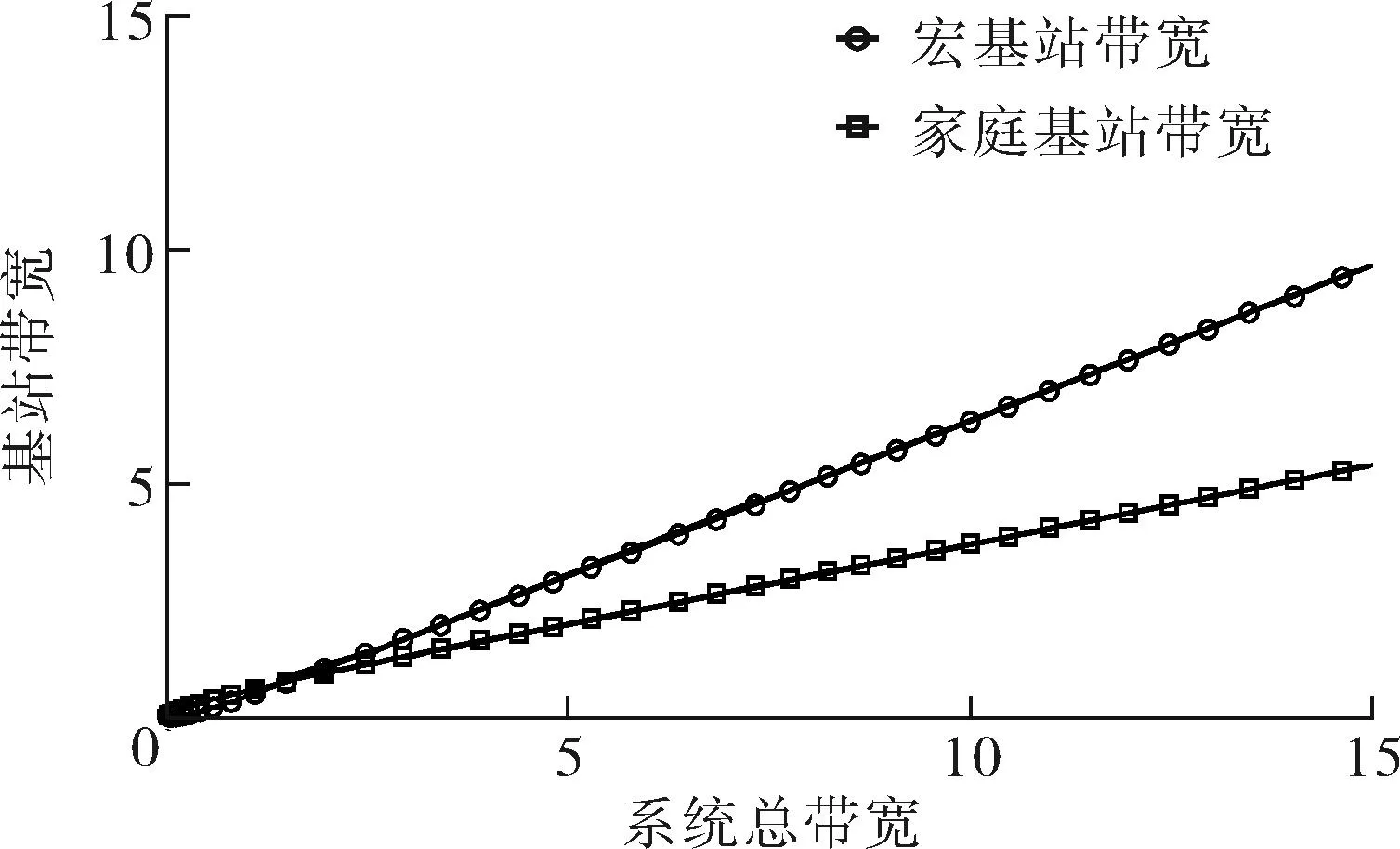
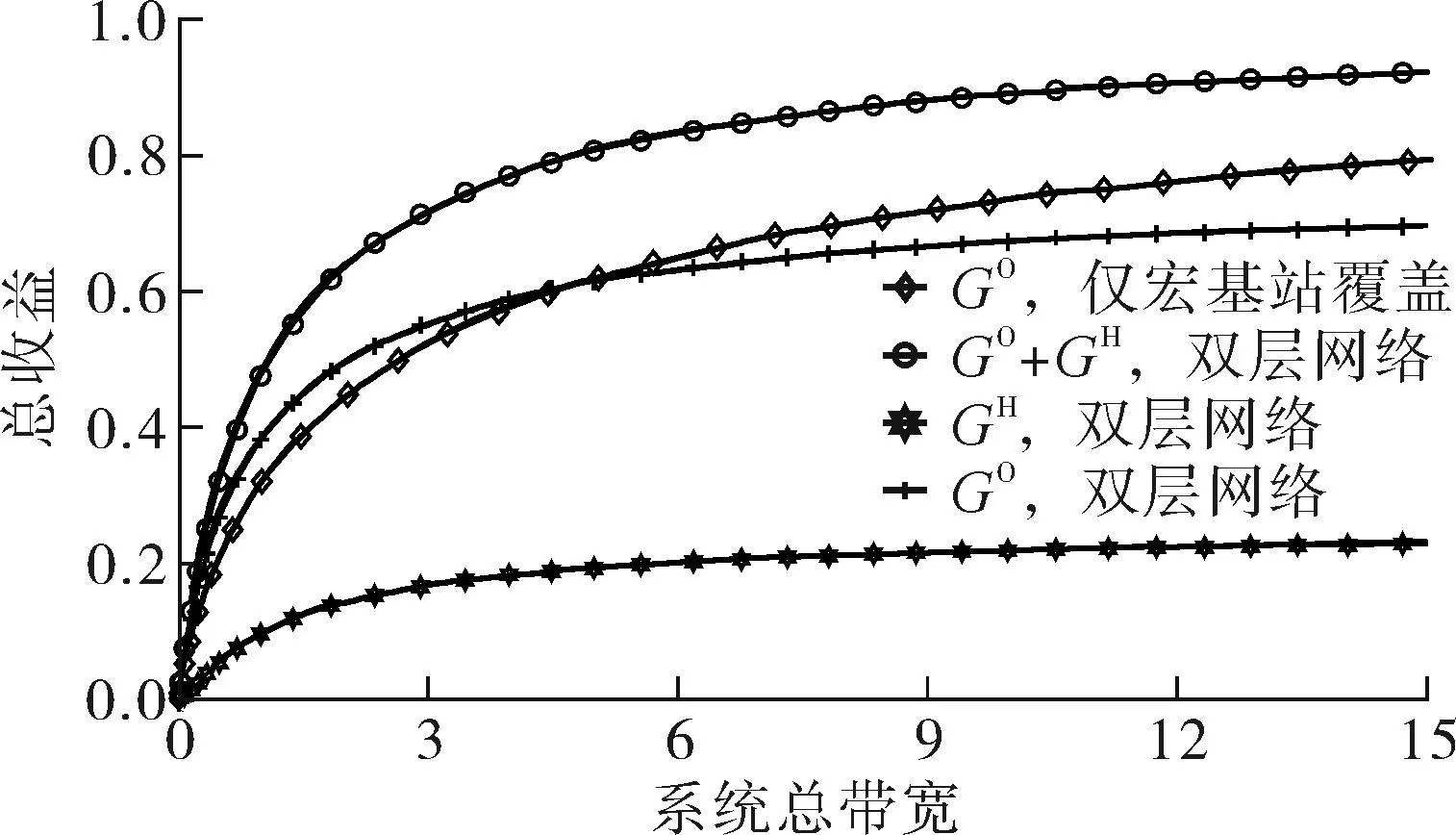
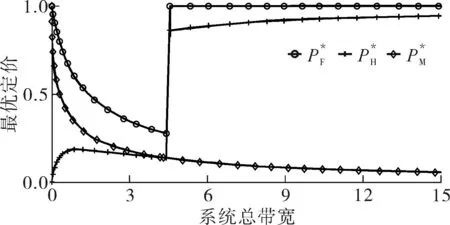
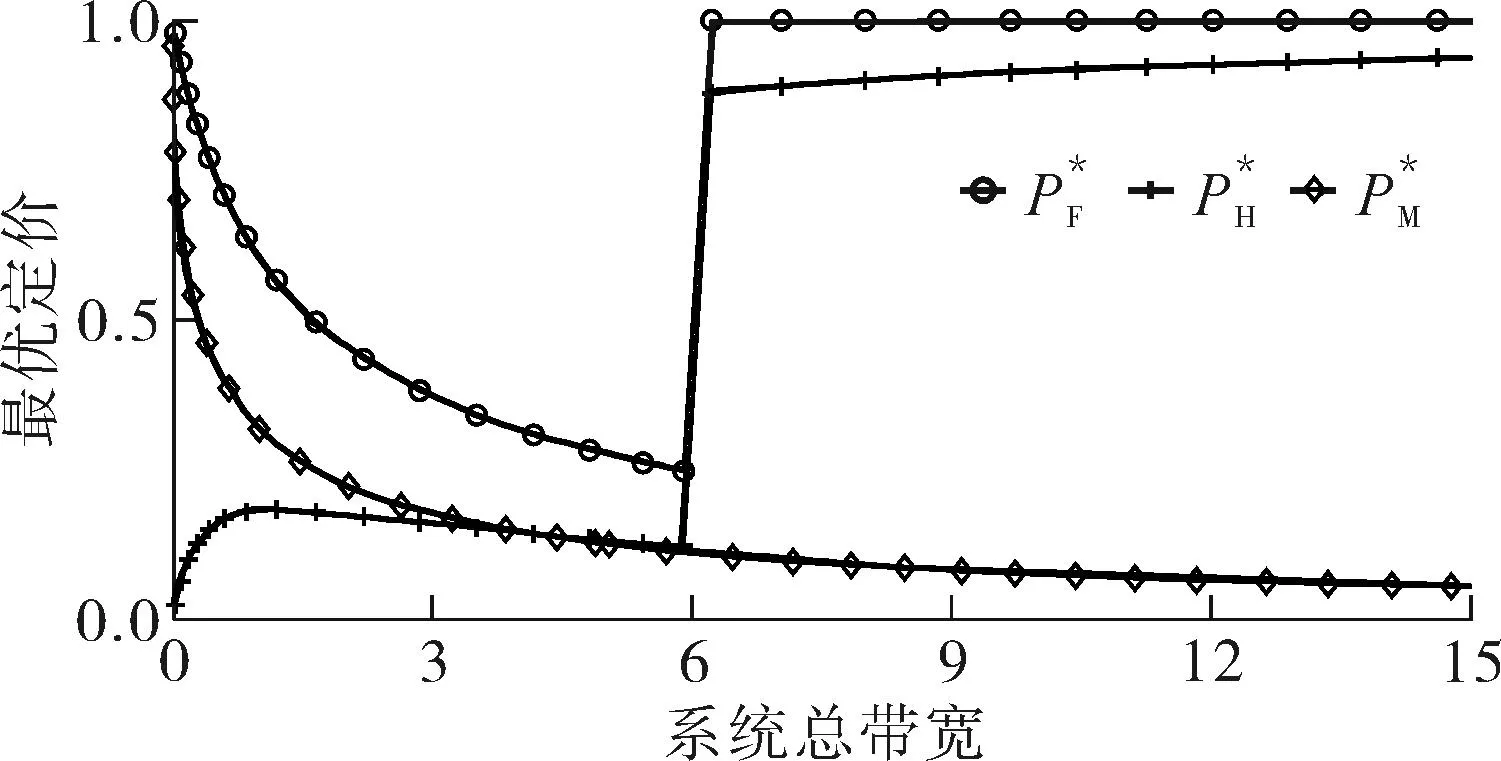
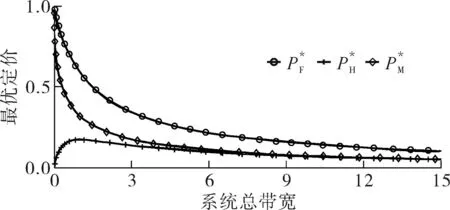
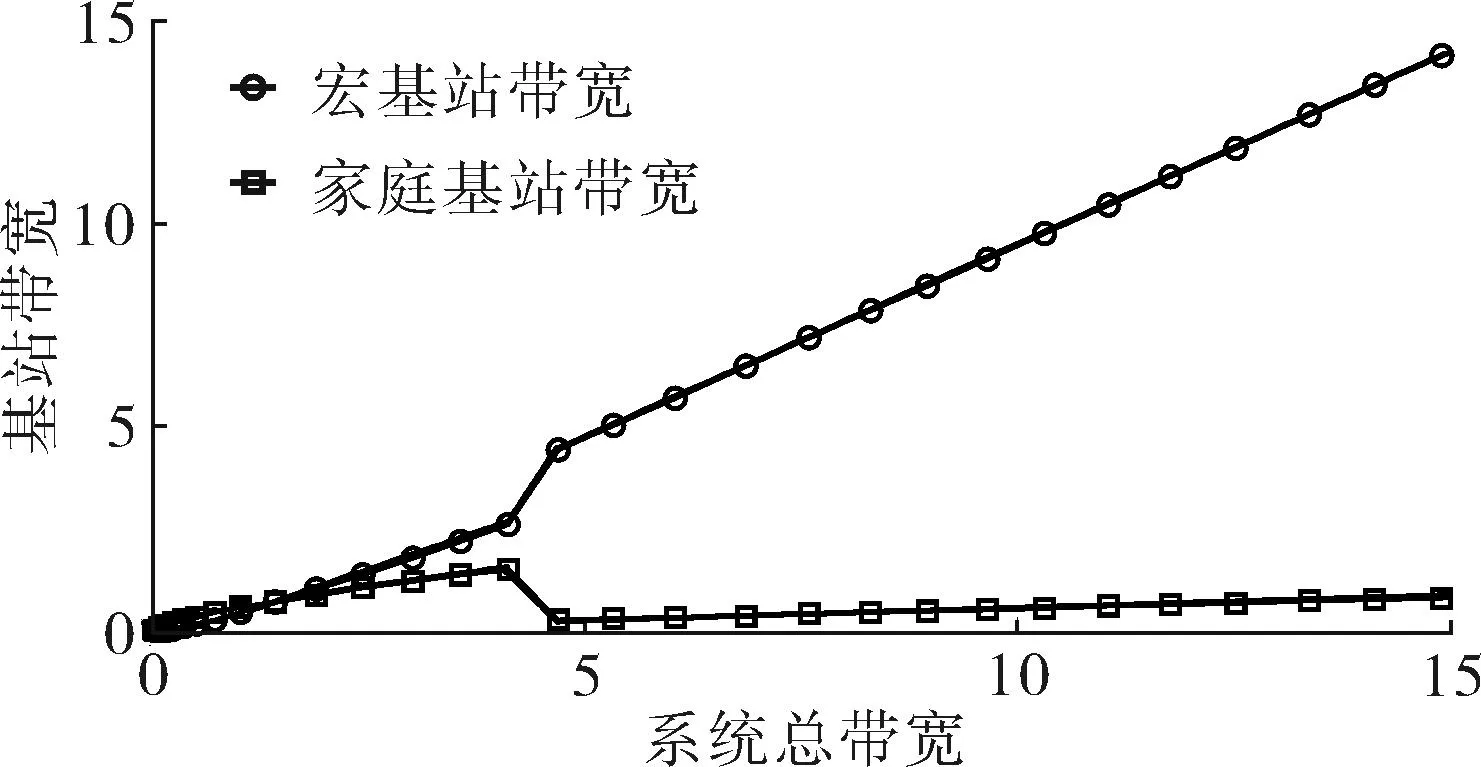
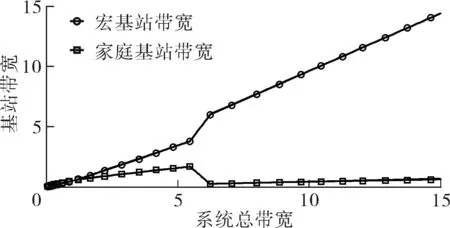
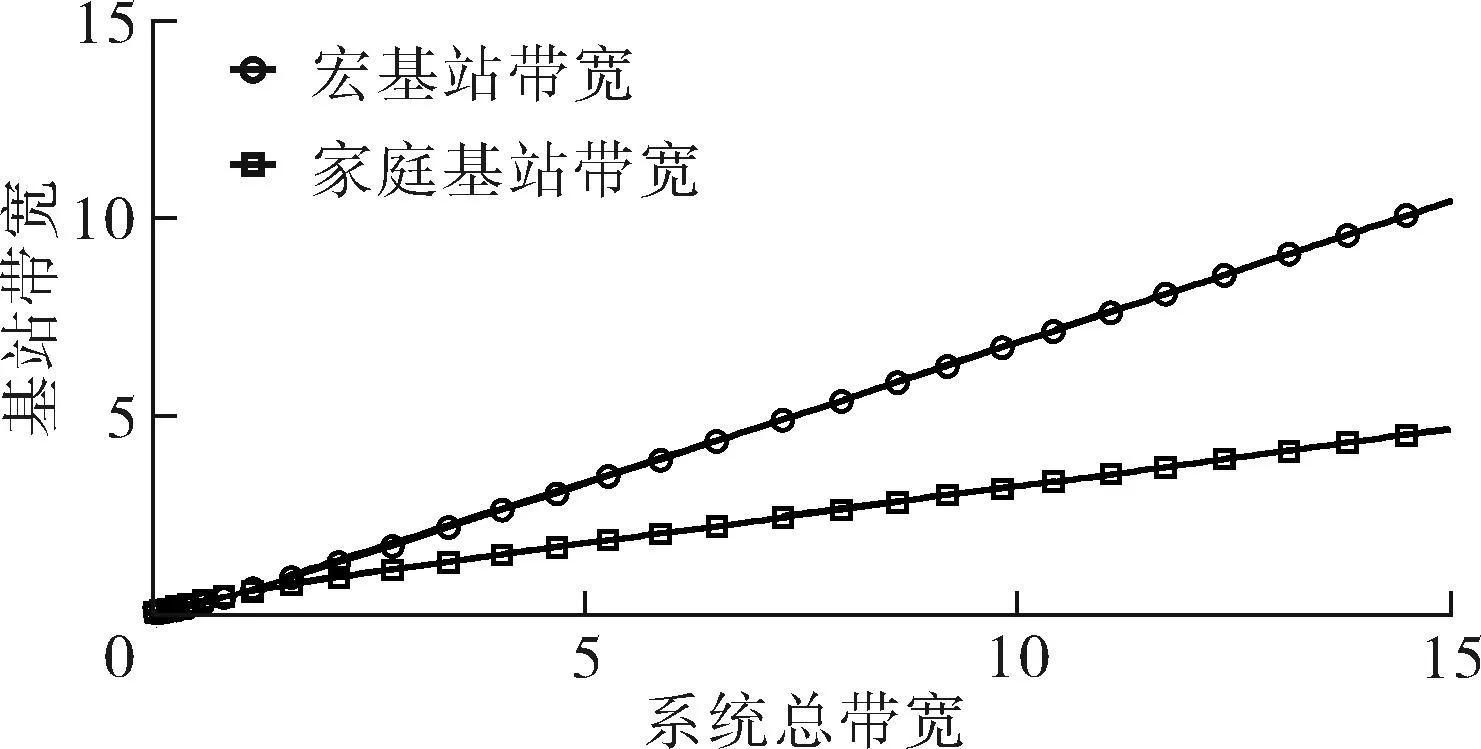
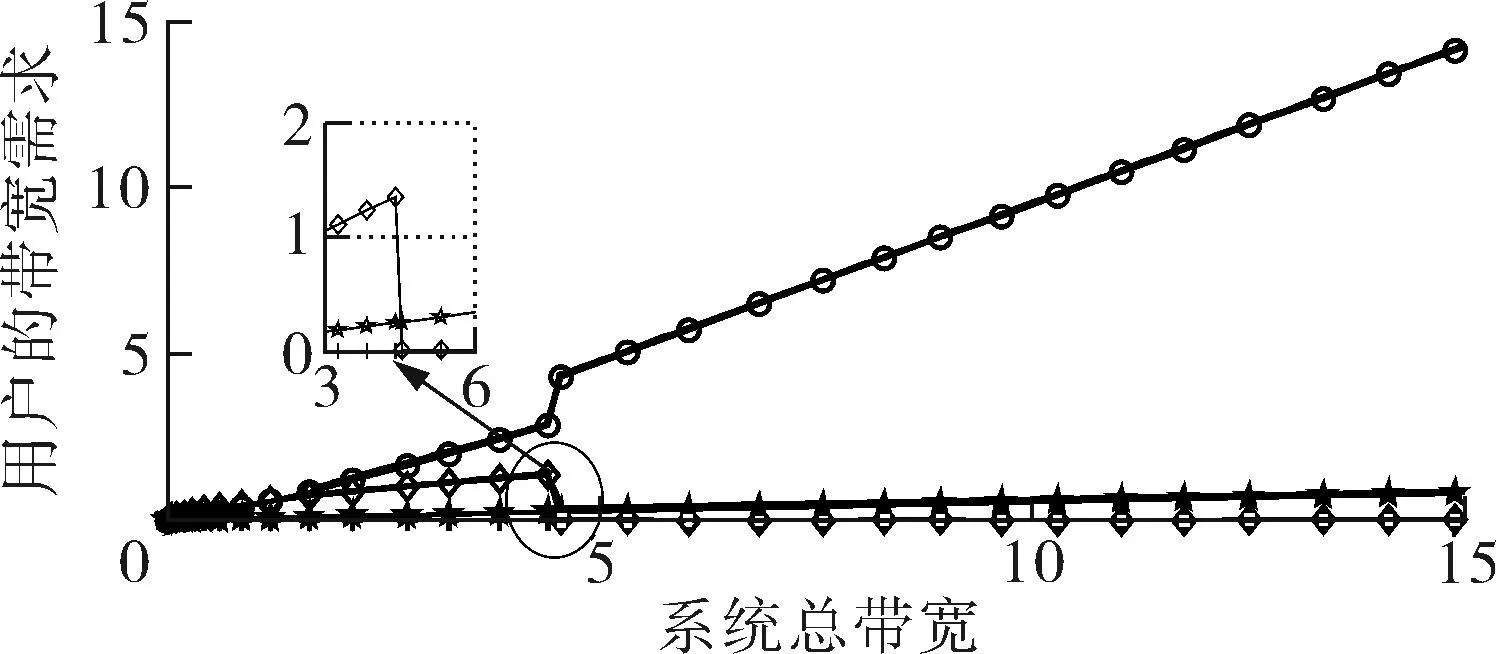
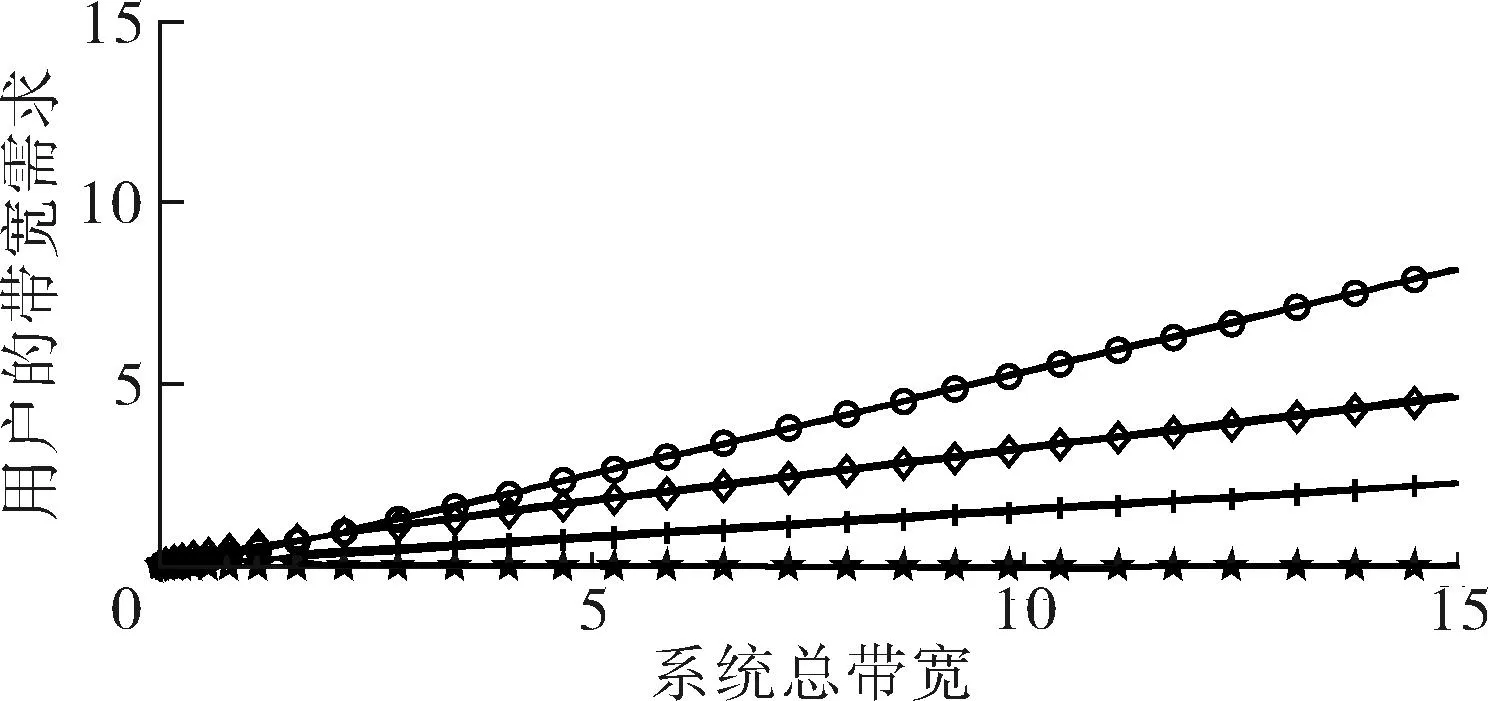
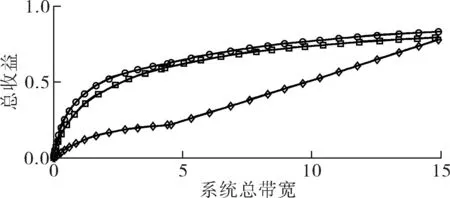
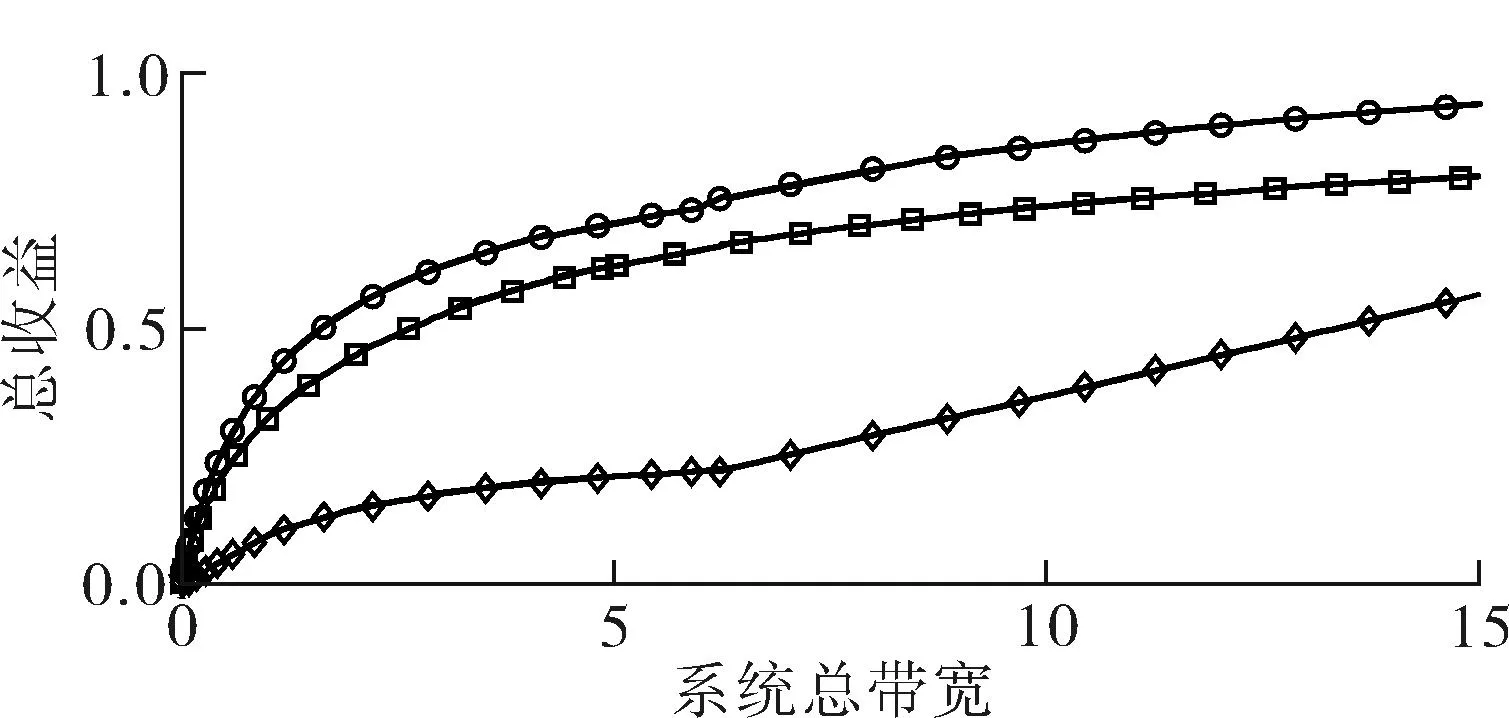
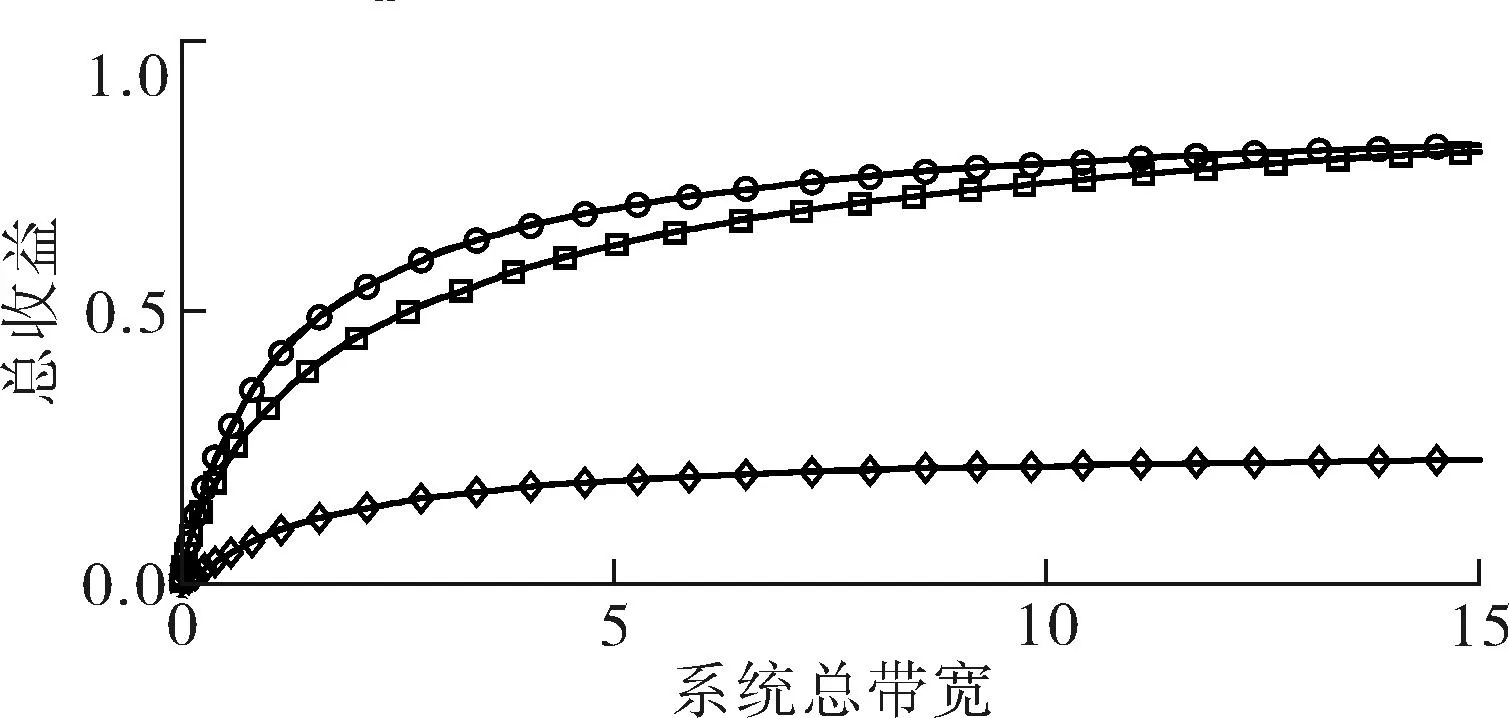
令M-BRUE、F-BRUE以及RUE的需求占所有用户需求的比例分别为β1、β2和β3，β1+β2+β3=1.与上一节讨论情况相同，只需讨论pM

DM-BRUE∶DF-BRUE∶(DF-RUE+DM-RUE)=β1∶β2∶β3

(23)

可以推出DM-BRUE与DF-BRUE分别为：

(24)

(25)

此时，运营商能获得频谱效益GO与家庭基站拥有者能获得的频谱效益GH分别为：

GO=pM(DM-BRUE+DM-RUE)+αpM(DF-RUE+DF-BRUE)

(26)

GH=pHDF-BRUE+pHDF-RUE

(27)

(28)

(29)

其中，约束条件为系统总带宽不小于3类用户的总购买量.与式(22)情形相同，对于式(28)与式(29)描述的最优化问题，虽然同样无法给出闭式解，却可采用遍历方法求解.此时，宏基站应当分配的带宽BM以及家庭基站的带宽BF分别为：

BM=DM-BRUE+DM-RUE

(30)

BF=DF-RUE+DF-BRUE

(31)

2.4策略分析

文中对频谱分配与定价策略的求解结果是采用逆向递归求解得来的，在Stackelberg博弈中，该结果是博弈双方互利的均衡点，即文中结果达到了Stackelberg均衡[14].

3仿真结果与分析

3.1仅存在理性用户的场景

在仅存在理性用户的场景下，宏基站与家庭基站的最佳定价分别如式(21)与式(22)所示.在仿真过程中，笔者将利益保证系数设定为1，如何选择最佳利益保证系数α，可作为进一步研究的问题.

图2　仅存在理性用户场景下家庭基站与宏基站的最优定价 Fig.2　Optimal prices of macrocell and femtocell in scenario involving only rational users

此场景下，宏基站与家庭基站应当按需分配的带宽分别如式(16)、(17)所示，相应仿真结果如图3所示，从图中可以看出，文中所提策略合理地分配了运营商的全部可用注册频谱资源.

图3　仅存在理性用户场景下宏基站与家庭基站频谱分配结果 Fig.3　Spectrum allocation for macrocell and femtocell in scenario involving only rational users

运营商与家庭基站拥有者所得频谱效益如图4所示.图中分别列出了在不同系统带宽下，双层分级蜂窝网络中，运营商的频谱效益、家庭基站拥有者的频谱效益、家庭基站与宏基站的频谱效益总和，并给出了仅宏基站覆盖下运营商的频谱效益作为参考.从图中可以看出，通过文中策略，宏基站与家庭基站的总频谱效益始终大于仅部署宏基站时获得的收益，频谱使用效率提高约17%.在双层分级网中，当频谱带宽较小时，运营商获得的利益大于仅部署宏基站时获得的利益，当频谱资源充足时，由于家庭基站引入的竞争关系，降低了频谱单价，运营商此时获得的频谱效益略小于仅部署宏基站时的频谱效益.然而，虽然运营商在频谱效益上有所损失，但是其最大效益损失仅12%，而运营商将大幅降低无线覆盖的建设、运营和耗能成本.综上，该定价策略有利于运营商与消费者在广泛部署家庭基站上获得双赢.

图4　运营商与家庭基站拥有者所得利益 Fig.4　Profits for service provider and femtocell base station holder

3.2包含有限理性用户的场景

当存在有限理性用户时，宏基站与家庭基站的最佳定价分别如式(28)和式(29)所示，同样将运营商利益保障系数设定为1.进行仿真时，采用多组不同类型用户比例作为对比，其中β1=15%,β2=4%,β3=81%分别代表包含M-BRUE、F-BRUE以及RUE3类用户；β1=15,β2=0%,β3=85%代表只包含M-BRUE和RUE两类用户；β1=0,β2=6%,β3=94%代表只包含F-BRUE和RUE两类用户；共3种不同的情形.

从图 5可以看出，场景中只要包含了F-BRUE，家庭基站定价就会存在跳变，pF会被抬高到其取值上限.之所以会出现这样的情况，是因为场景中包含F-BRUE，当F-BRUE带宽需求数量较多，满足DF-RUE∶DF-RBUE=(1-pH)∶pH时，家庭基站将pF抬高到上限，即使流失理性用户，总收益仍然有提高，因此，家庭基站拥有者为最大化其总效益，将pF定为最高价格，从而出现了家庭基站定价的跳变.而当场景中不存在F-BRUE时，不会有价格跳变的情况出现.而对于宏基站，由于其覆盖范围内，不同位置的频谱效率各不相同，只有当c≥pM时，用户才会接入宏基站.因此，宏基站若非理性地抬高价格，理性用户和有限理性用户都将流失，因此，宏基站价格不会因为有限理性用户的存在而出现跳变.实际中，可在运营过程统计不同类型用户的比例，进而获得最优定价策略.

(a)β 1=0,β 2=6%,β 3=94%

(b)β 1=15%,β 2=4%,β 3=81%

(c)β 1=15%,β 2=0,β 3=85% 图 5　包含有限理性用户场景中家庭基站与宏基站的最优定价 Fig.5　Optimal prices of macrocell and femtocell in scenario involving irrational users

宏基站与家庭基站应当按需分配的带宽分别如式(30)、(31)所示，仿真结果如图 6所示.在包含F-BRUE的场景中，当家庭基站价格出现跳变时，理性用户将放弃家庭基站而选择宏基站，相应地，应当减少家庭基站带宽，增大宏基站带宽，以满足用户需求.由图可知，理性用户放弃家庭基站的跳变点与家庭基站定价突增点相同.

(a)β 1=0,β 2=6%,β 3=94%

(b)β 1=15%,β 2=4%,β 3=81%

(c)β 1=15%,β 2=0,β 3=85%

图 6包含有限理性用户场景中宏基站与家庭基站频谱分配结果

Fig.6Spectrum allocation between macrocell and femtocell in scenario involving irrational users

图 7进一步描述了各类用户所占带宽资源.该图表明，F-BRUE通过高价抢占家庭基站资源后，理性用户放弃家庭基站而选择宏基站.为合理分配频谱资源，需相应地从家庭基站转移部分带宽至宏基站.图 6与图 7有很好的一致性.

(a)β 1=0,β 2=6%,β 3=94%

(b)β 1=15%,β 2=4%,β 3=81%

(c)β 1=15%,β 2=0,β 3=85%

图7包含有限理性用户场景中用户带宽需求与系统总带宽的关系

Fig.7Relationship between user demand and bandwidth in scenario involving irrational users

从图 8可以看出，在存在有限理性用户的场景中，运营商在家庭基站的部署过程中，获得了比仅部署宏基站更高的频谱效益，同时家庭基站拥有者也从家庭基站中获得了最大化的效益.在家庭基站定价突增之后，定价保持最高价，因而其效益随服务带宽呈现线性增长方式.在3种情况下，双层分级蜂窝网络相比仅部署宏基站时，频谱使用效率分别提高约102%、88%和30%.

(a)β 1=0,β 2=6%,β 3=94%

(b)β 1=15%,β 2=4%,β 3=81%

(c)β 1=15%,β 2=0,β 3=85%

图8包含有限理性用户场景中运营商与家庭基站拥有者利益

Fig.8Profits for service provider and femtocell base station holder in scenario involving irrational users

3.3仿真结果

从上述仿真实验可知，仿真结果与理论推导有较强的一致性，频谱资源定价对用户需求的影响反应了资源的供需关系随价格变化的特性，宏基站与家庭基站合理地共享了运营商所拥有的带宽资源.由于家庭基站有更高的频谱效率，其定价会略高于宏基站，使用相同带宽获得的效益更大.在有限理性用户中，M-BRUE不会干扰家庭基站的定价，并且其对宏基站定价的影响与理性用户相同.所以F-BRUE不会干扰宏基站定价，但是会抬高家庭基站定价，以高价的方式抢占家庭基站的频谱资源.

4结语

在双层分级蜂窝网中，文中采用Stackelberg博弈模型，分析了频谱资源价格与用户需求的关系，分别对包含理性用户以及有限理性用户的场景，给出了宏基站与家庭基站异频组网的定量带宽分配方案，并对频谱资源进行了定价，最大化了运营商以及家庭基站拥有者获得的频谱效益；仿真结果与理论推导有较强的一致性.采用文中所提方案，能有效促进运营商与用户共同推进家庭基站部署，激励家庭基站拥有者采用开放用户组模式，从而提高无线通信的有效覆盖.

参考文献：

[1]Andrews J G,Buzzi S,Choi W,et al.What will 5G be? [J].IEEE Journal on Selected Areas in Communications,2014,32(6)：1065-1082.

[2]Zhou X,Feng S,Ding Y,et al.Game-theoretical frequency reuse method for complex cognitivefemto-cell network [C] ∥Proceedings of 2013 8th International ICST Conference on Communications and Networking in China (CHINACOM).Guilin：IEEE,2013:318-322.

[3]Huang J W,Krishnamurthy V.Cognitive base stations in LTE/3GPPfemtocells:a correlated equilibrium game-theoretic approach [J].IEEE Transactions on Communications,2011,59(12):3485-3493.

[4]Lien S Y,Lin Y Y,Chen K C.Cognitive and game-theoretical radio resource management for autonomous femtocells with QoS guarantees [J].IEEE Transactions on Wireless Communications,2011,10(7):2196-2206.

[5]Xie R,Yu F R,Ji H,et al.Energy-efficient resource allocation for heterogeneous cognitive radio networks with femtocells [J].IEEE Transactions on Wireless Communications,2012,11(11):3910-3920.

[6]Lin P,Zhang J,Chen Y,et al.Macro-femto heterogeneous network deployment and management:from business mo-dels to technical solutions [J].IEEE Wireless Communications,2011,18(3)：64-70.

[7]Duan L,Huang J.Economic viability of femtocell service provision [C]∥Proceedings of 2nd International ICST Conference.Berlin,Heidelberg：Springer,2012:413-428.

[8]Yun S,Yi Y,Cho D H,et al.Open or close:on the sharing offemtocells [C] ∥Proceedings of IEEE INFOCOM 2011.Shanghai:IEEE,2011:116-120.

[9]Claussen H,Ho L T W,Samuel L G.Financial analysis of a pico-cellular home network deployment [C] ∥Proceedings of IEEE International Conference on Communications,2007.Glasgow:IEEE,2007：5604-5609.

[10]Shetty N,Parekh S,Walrand J.Economics of femtocells [C] ∥Proceedings of Global Telecommunications Conference,2009.Honolulu:IEEE,2009：1-6.

[11]Chen Y,Zhang J,Zhang Q.Utility-aware refunding framework for hybrid accessfemtocell network [J].IEEE Transactions on Wireless Communications,2012,11(5):1688-1697.

[12]Shen H,Basar T.Optimal nonlinear pricing for a mono-polistic network service provider with complete and incomplete information [J].IEEE Journal on Selected Areas in Communications,2007,25(6):1216-1223.

[13]Leung K,Huang J.Regulating wireless access pricing [C] ∥Proceedings of 2011 IEEE International Confe-rence on Communications (ICC).Kyoto:IEEE.2011:1-5.

[14]Fudenberg D,Tirole J.Game theory [M].Cambridge:The MIT Press,1991.

[15]Weibull J W.Evolutionary game theory [M].New York:MIT Press,1997.

Optimal Allocation and Pricing Strategy for Spectrum Resources on the

Basis of Stackelberg Game

ZhouXiongFengSui-li

(School of Electronic and Information Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:In order to solve the problems existing in the deployment and operation of femtocell base stations as well as in the spectrum resource share between femtocells and macrocells, an optimal allocation and pricing strategy for spectrum resources is proposed on the basis of Stackelberg game. By modeling the game between base stations and users, the relationship between spectrum price and user demands is analyzed. Then, by modeling the game between macrocells and femtocells, an optimal strategy of spectrum allocation and pricing in various scenes is proposed for two-tiered hierarchical cellular networks. This strategy allocates spectrum resources between macrocells and femtocells reasonably, maximizes their utility, effectively inspires operators and owners to deploy femtocell base stations, and promotes the process of green communication.

Key words: two-tiered hierarchical cellular network; Stackelberg game; spectrum allocation; spectrum pricing

Foundation items: Supported by the National High-tech R&D Program (863 Program)(2014AA032702) and the National Natural Science Foundation of China(NSFC)(61204087, 51173049, 61306099)