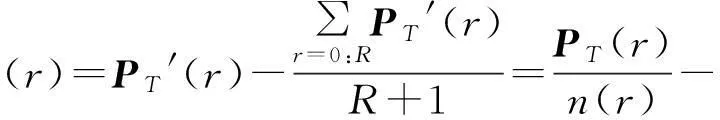基于ASIFT和圆投影特征的图像被动取证

基于ASIFT和圆投影特征的图像被动取证*

赵俊红哀微朱学峰

(华南理工大学 自主系统与网络控制教育部重点实验室， 广东 广州 510640)

摘要：文中针对图像篡改中最常见的复制粘贴篡改被动取证问题展开图像分析研究，提出了一种基于仿射尺度不变特征变换(ASIFT)和圆投影特征的算法，用于检测图像中是否存在复制粘贴篡改.实验结果表明：基于仿射尺度不变特征的算法对具有明显角点特征的篡改图像的取证效果较好，而基于改进圆投影特征的算法对不具备明显角点特征的篡改图像(如随机性纹理、平坦区域)的取证效果较好，因此联合使用基于这两种特征的算法对常见的复制粘贴型图像篡改进行被动取证能达到较好效果.

关键词：复制粘贴篡改；图像分析；仿射尺度不变特征变换；圆投影；被动取证

中图分类号：TN911.37

doi：10.3969/j.issn.1000-565X.2015.03.010

文章编号：1000-565X(2015)03-0072-06

收稿日期：2014-08-13

基金项目：* 广东省-国家自然科学联合基金资助项目(U1035002)；广东省教育厅校企合作项目(CGZHZD1102)；粤港科技攻关项目(2011A011305001,2011A011302001)

作者简介：李红涛(1977-)，男，博士生，讲师，主要从事无线通信系统的研究.E-mail: LHT88@126.com

数码技术的普及使得图像篡改变得容易和难以察觉，给数字图像带来严重的信任危机,对图像的真伪鉴别变得非常重要.因此直接利用图像信息的被动取证技术比需要事先添加数字水印或数字签名的主动取证技术具有更高的理论和应用价值.图像篡改中最常见的是复制/粘贴型篡改(即图像中部分内容经旋转、调节亮度等操作后再粘贴到同幅图像的其他位置从而达到篡改目的).

由于复制图像块和粘贴图像块源于同一幅图像，利用图像的统计特性来取证的方法失效.现有的方法可分为两大类：一类是将图像中的每一个小分块在整个大图像中进行检索匹配，如果能在跟原始位置不同的地方找到匹配图像块，则认为图像中存在复制/粘贴型篡改,可将图像分成互相重叠的小图像块构造高维数据，再对高维数据进行降维，然后按照一定的阈值对降维后的图像块进行相似性判断，最终找出同一图像中复制/粘贴区域.此类算法受图像分块大小和形状影响较大，且处理的信息量较大，速度较慢[1-3].另一类是提取图像特征信息(如傅里叶变换特征[4]、HARIS角点信息特征[5]、尺度不变特征变换特征(SIFT)[6-7]、非抽样小波变换特征[8]、泽尔尼克矩[9]等)，在整个图像中进行特征匹配，找到图像中位于不同位置的匹配点，从而判别是否存在复制/粘贴型篡改，该类算法由于通过提取图像中稳定且共有的特征进行匹配，在一定程度上压缩了信息量，提高了准确率和速度.但是现有的基于以上特征量的取证算法在复制和粘贴图像区域之间存在较大仿射变化时取证检测精度大大降低.

文中重点针对复制/ 粘贴区域存在较大仿射变化和亮度变换时的情况展开被动取证研究.

1仿射尺度不变特征变换算法

Yu 等[10]针对尺度不变特征变换特征(SIFT)的两个缺点——不具有完全仿射不变性和无法对抗大视角变换，提出仿射尺度不变特征变换算法(ASIFT).ASIFT模拟了相机运动的经度角、纬度角、尺度缩放，对旋转、平移、倾斜进行了归一化，所以能对抗大角度旋转和视点角度的较大变化.

1.1相机仿射变换模型

由文献[11]相机投影模型可知，相机获取图像为u=Σ1G1FΓu0.式中:u为数字图像；u0为平面物体的正视图，是一个具有无限分辨率的理想图像；Γ为相机位置移动所带来的图像平移量；F为相机位置移动所带来平面投影映射；Σ1为标准的间隔为1的采样操作；G1为高斯卷积模型，模拟了光学散斑模糊，并假设高斯核对于采样算子有足够的宽度来避免混叠.

ASIFT简化了上述模型，将平面投影图像简化成仿射图像[11],图像每个区域的所有局部投影效果模型中由于视角变换而造成的变形都用局部仿射变换模型表示，即u(x,y)→u(A(x,y)),A为仿射变换矩阵.

因此可以将有限距离的相机投影变换视为无限远处的多个相机的仿射变换(如图1所示)，这些相机会产生仿射变形.实际上相机的位置变换会产生具有正行列式的仿射映射.定理1形式化了此效果并给出对于仿射变形的相机运动的解释[11].

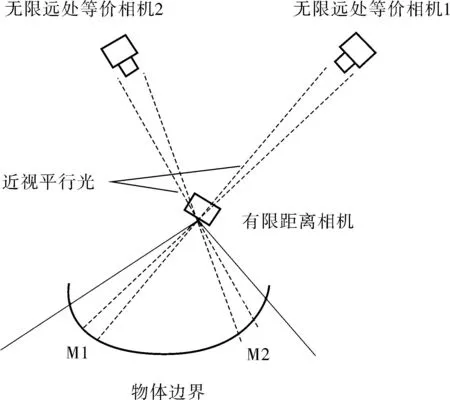
图1　相机模拟 Fig.1　Simulation of the camera

定理1任何一个具有严格正行列式的仿射变换矩阵A可分解成唯一形式：

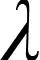
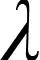
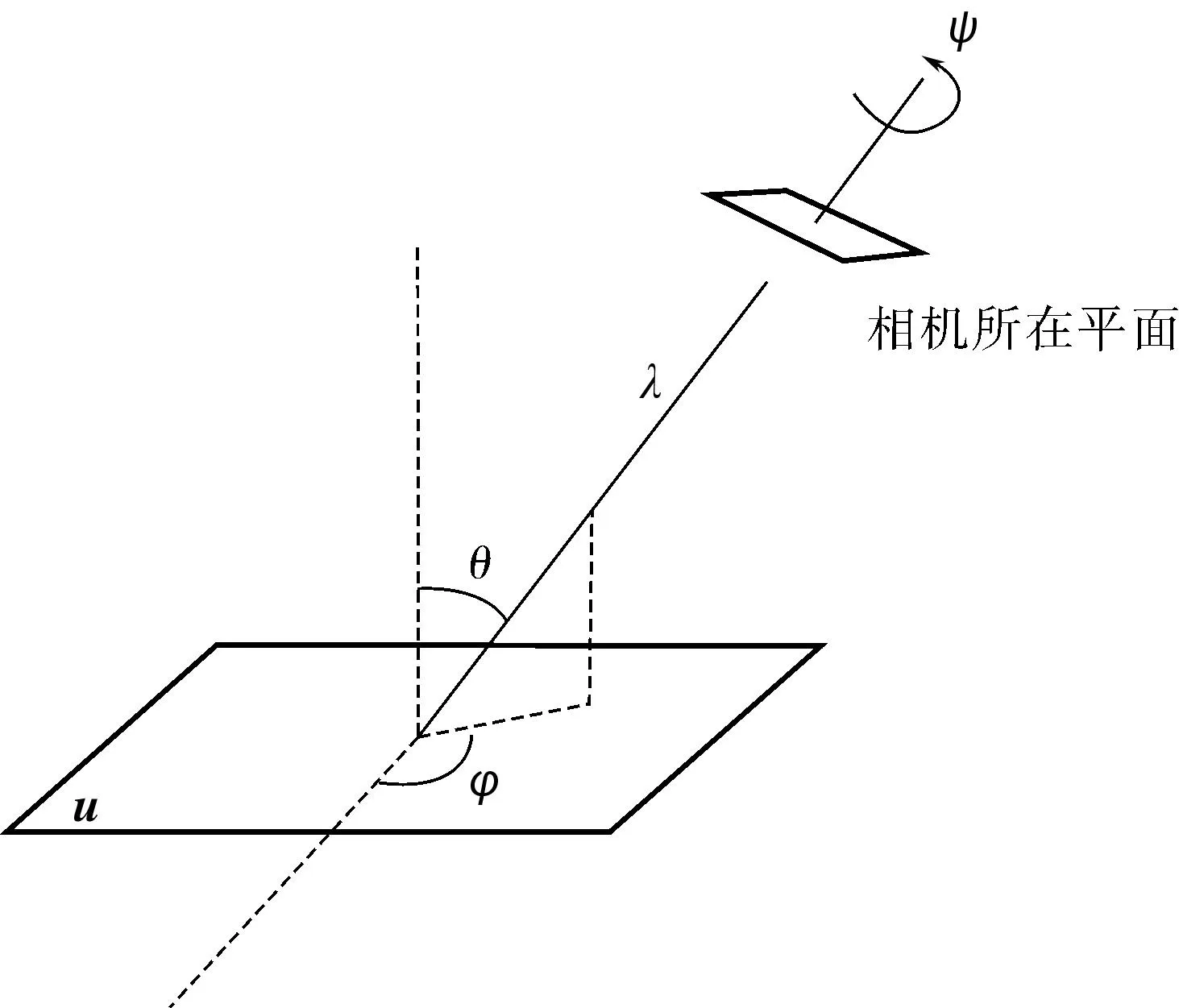
图2　相机的运动参数 Fig.2　Movement parameters of camera

1.2ASIFT算法步骤

该算法步骤如下：

(1)对待匹配的图像E、B分别改变φ进行旋转变换、改变θ进行倾斜变换，得到多个仿射变换图像Ei、Bi；

(2)对φ和θ的采样需遵守一定的原则[10]才能保证使用不同的φ和θ后得到的图像尽可能相似；

(3)对多个仿射变图像Ei、Bi两两使用SIFT算法进行匹配.

1.3图像复制/粘贴篡改取证

文中首次将ASIFT应用到图像被动取证中，用来检测同幅图像中的复制粘贴，算法如下：将图像进行ASIFT处理,找到图像中匹配上的特征点；设定单位面积中匹配上特征点个数n的阈值nth,当n>nth时则认为图像中存在复制/粘贴.

图3中篡改图像是将原图左下角圆形区域的图像经过一定的缩放比例s、旋转角度θ后粘贴在右上角圆形区域.图3中的检测结果显示，基于ASIFT算法的取证算法能有效检出，而现有的基于SIFT的取证算法失效，即在复制区域和粘贴区域之间存在较大角度旋转和较大尺度变化时基于ASIFT的取证算法比现有的基于SIFT的取证对仿射变换具有更好的鲁棒性.

图4是利用这两种算法对多幅图像进行取证的结果.其中，图4(a)-(d)已知篡改手段，图4(e)、(f)未知篡改手段，图4(c)中出现较多误匹配的原因是被复制的元件和图中其他3个元件是一样的元件.

(a)原图

篡改图 1ASIFT检测SIFT检测

(s=0.8,θ=20° )(22点)(0点)

(b)篡改图1

篡改图2ASIFT检测SIFT检测

(s=0.8,θ=50°)(17点)(0点)

(c)篡改图2

篡改图 3ASIFT检测SIFT检测

(s=0.8,θ=80°)(15点)(0点)

(d)篡改图3

篡改图4 ASIFT检测SIFT检测

(s=0.5,θ=10°)(16点)(0点)

(e)篡改图4

篡改图5ASIFT检测SIFT检测

(s=1.2,θ=10°)(25点)(0点)

(f)篡改图5

篡改图6 ASIFT检测SIFT检测

(s=2.0,θ=10°)(27点)(0点)

(g)篡改图6

图3ASIFT取证图像

Fig.3Forensic images of ASIFT

原图 篡改图(θ=30°) ASIFT(16点) SIFT(0点)

(a)风车

原图篡改图(θ=40°)ASIFT(34点)SIFT(0点)

(b)沙漠

原图　　篡改图( s=1.4) ASIFT(171点)　SIFT(0点)

原图 篡改图(异向放大) ASIFT(57点)SIFT(0点)

(d)山水

原图 篡改图 ASIFT检测SIFT检测

(e)草坪

原图　　 　 　篡改图　　　 ASIFT检测　 　SIFT检测

但是ASIFT不能检测出无明显角点的图像(如图5(a)随机性纹理、平坦区域图像)，也不能检查如图5(b)这类照度变化较大的图像.

(a)具有平坦区域的篡改图(b)篡改位置照度发生剧烈变化的图

图5ASIFT不能检测的图像

Fig.5The images unable to be detected by ASIFT

2圆投影特征算法

针对上述ASIFT的缺陷，拟将另一种特征量——圆投影引入被动取证算法中.

雷当(Radon)变换能利用图像在0°到180°之间的所有系列平行线的积分即投影完全精确重建该图像[12]，因此可将投影数据作为特征量.文献[13]使用图像水平投影和垂直投影作为图像的特征量解决了复制/粘贴型取证算法中数据维数过高的问题，加快了速度，但是未能解决光照不变性和旋转不变性,因此将圆投影引入被动取证算法中，使得算法具有旋转不变性和光照不变性.

2.1圆投影原型

圆具有旋转不变性，圆投影即是计算圆内不同半径同心圆内的像素之和作为该半径的投影数据[14-15].

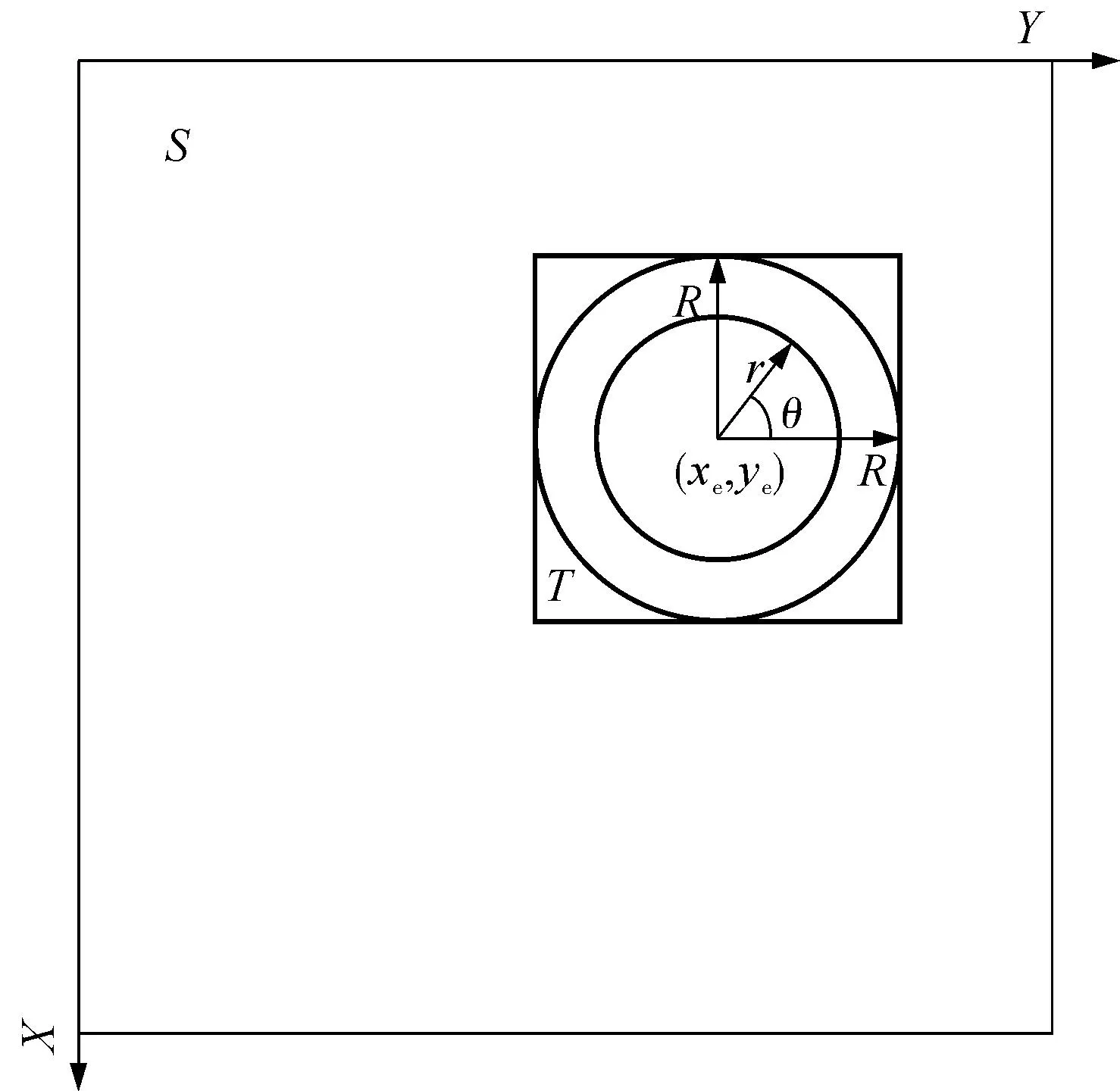
图6　圆投影定义 Fig.6　Definition of ring projection transformation

PT=(P(0),P(1),…,P(R))

(2)

由定义可知，P(r)是一个旋转不变量，能抵抗任意角度旋转攻击.

在图像篡改时，复制图像块和粘贴处图像块之间还经常会有亮度调节和添加.分析式(2)发现，随着半径的增大，投影数据值逐渐增大PT(0)

2.2圆投影的改进

文献[10]利用每一同心圆的灰度均值代替投影值，以此抵抗加性白噪声攻击，即投影量中的每一个分量为

PT′(r)=PT(r)/n(r)

(3)

式中，n(r)为半径为r的同心圆中像素点的个数.由于亮度变化给图像加上了一个直流分量，需要减去一个与该直流分量大小相似的量才能抵抗亮度变化的影响.

文献[16]在式(2)的基础上做以下改进：

(4)

文中对圆投影进行改进如下：

(5)

式(5)与式(4)都减去一个估计的直流分量，不同的是，式(4)是直接用原始投影进行估计，而式(5)直流分量是用过滤了噪声的投影数据进行估计,相当于对该分量进行了两次低通滤波，可进一步减小噪声对直流分量估计值的影响.

2.33种圆投影计算方法的验证

2.1和2.2中分析了圆投影原型和两种改进方法的优缺点，此节针对上述几种投影方法进行验证.

图7(a)图像经旋转60°、加噪声(高斯噪声，均值为零，σ=0.01)、亮度调节(γ校正，γ=0.6)后得图7(b).图7(a)中，N为以 (151,77)为圆心，半径为7的图像数据，由式(3)-(5)得到在图7(a)的圆投影值：

(a)原图(b)亮度调节/加噪/旋转处理后图像

图7原图和处理后图像

Fig.7Theoriginalimageandthemanipulatedone

PTa′=[44.00025.60018.46215.37914.592

14.13614.15914.107]，

PTa″=[29.396310.99633.85830.7753

-0.0117-0.4677-0.4447-0.4967]，

PTa‴=[23.94565.5456-1.5924-4.6754

-5.4624-5.9184-5.8954-5.9474].

该图像N旋转60°后得到圆心为(184,122)，半径为7的图像数据M，由式(3)-(5)得到图7(b)的圆投影值：

PTb′=[60.741080.332785.055378.387073.088171.300670.798269.9312]，

PTb″=[40.700627.41257.5761-0.4208

4.3521-0.2244-1.7570-1.7493]，

PTb‴=[45.70378.8893-2.3435-15.3943

-16.6847-9.8302-4.8578 -5.4851].

由图7(a)和图7(b)的关系可知，M在N的基础上经过了一系列操作(这些操作往往是篡改的手段).但是图像数据M和图像数据N所反映的图像内容是一致的，因此希望图像N和M的相似性较高.

文中采用相关系数来表征二者间的相似性，相关系数越大表示图像数据之间一致性越强.

分别计算圆投影值之间的相关系数α(PTa,PTb)，其中PTa、PTb分别为图7(a)和(b)的圆投影值，得

α(PTa′,PTb′)=0.4691，

α(PTa″,PTb″)=0.9588，

α(PTa‴,PTb‴)=0.9731.

可见文中提出的相似圆投影改进方法(式(5))具有更强的抗噪、抗图像旋转、抗亮度变化的能力.

2.4基于改进的圆投影特征的取证

2.4.1算法流程

基于改进的圆投影数据的图像复制粘贴取证算法类似于文献[1,7]，算法如下：

(1)将待取证图像I逐行逐列的分成互相重叠的小图像块Ki,i=1,2,...,l；

(2)按照式(5)计算每个小图像块PTi‴,i=1,2,...,l值构成一个高维矩阵Q(m,t),m=1,2,...,l;t=r+1；

(3)利用主元分析法对Q(m,t)降维得到Q(m,t′),t′

(4)对算Q(m,t′)相邻行之间相关系数α，如果α大于设定好的相关系数阈值αth且这相邻行所代表的图像块在待取证图像中的距离大于设定好的距离阈值dth，则认为这两个图像块之间为复制/粘贴图像块；否则，继续寻找Q(m,t′)的相邻行.

2.4.2图像复制粘贴篡改取证结果

对图5，运用ASIFT无法完成取证，采用改进的圆投影数据进行取证的结果如图8所示，其中圆投影半径r为3，相关系数阈值αth=0.93，dth设定为20个像素.

Fig.8Results of passive forensics based on a improved circle projection

3结语

针对同一图像内的复制/粘贴被动取证，通过研究发现可以分别运用仿射尺度不变特征变换算法(ASIFT)和圆投影数据作为特征量进行取证.研究发现：对具有明显的角点信息的图像可选用仿射尺度不变特征变换算法，当匹配上的图像像素点数大于某一阈值时，认为图像中存在复制/粘贴型篡改；对于纹理图像、平坦区域或复制/粘贴图像块之间存在亮度变化时可选用文中的改进圆投影数据进行取证，结果显示联合使用这两种方法对图像取证效果良好.下一步应研究如何融合这两种方法.

参考文献：

[1]Popescu A C,Farid Hanny.Exposing digital forgeries by detecting duplicated image regions[R].Dartmouth:Department of Computer Science,Dartmouth College,2004：1-11.

[2]Jessica Fridrich,David Soukal,Jan Lukas.Detection of copy-move forgery in digital images[C/OL]∥Proceedings of Digital Forensic Research Workshop.http:∥www.ws.binghamton.edu/fridrich/research/copymove.pdf.

[3]Sevinc Bayram,Husrev Taha Sencar,Nasir Memon.An efficient and robust method for detecting copy-move forgery[C]∥Proceedings of the 34th International Conference on Acoustics,Speech,and Signal Processing.Taipei:IEEE,2009:1053-1056.

[4]Ketenci S,Ulutas G.Copy-move forgery detection in images via 2D-Fourier transform [C]∥Proceedings of the 36th International Conference on Telecommunications and Signal Processing.Rome:IEEE,2013:813-816.

[5]Chen Li-kai,Lu Wei,Ni Jiang-qun,et al.Region duplication detection based on Harris corner points and step sector statistics [J].Journal of Visual Communication and Image Representation,2013,24(3):244-254.

[6]Amerini Irene,Ballan Lamberto,Caldelli Roberto,et al.A SIFT-based forensic method for copy-move attack detection and transformation recovery [J].IEEE Transactions on Information Forensics and Security,2011,6(3):1099-1110.

[7]Jaberi Maryam,Bebis George,Hussain Muhammad,et al.Accurate and robust localization of duplicated region in copy-move image forgery [J].Machine Vision and Applications,2014,25(2):451-475.

[8]Muhammad G,Hussain M,Khalid Khawaji,et al.Blind copy move image forgery detection using dyadic undecimated wavelet transform [C]∥Proceedings of the 17th International Conference on Digital Object Identifier.Corfu:IEEE,2011:1-6

[9]Ryu Seung-jin,Krichner Matthias,Lee Min-jeong,et al.Rotation invariant localization of duplicated image regions based on Zernike moments [J].IEEE Transactions on Forensics and Security,2013,8(8):1355-1370.

[10]Yu Guoshen,Morel Jean-Michil.A fully affine invariant image comparison method[C]∥Proceedings of the 34thInternational Conference on Acoustics,Speech,and Signal Processing.Taipei:IEEE,2009:1597-1600.

[11]Jean-Michil Morel,Guoshen Yu.ASIFT:a new framework for fully affine invariant image comparison[J/OL].[2014-06-06].http:∥www.cmap.polytechnique.fr/～yu/publications/ASIFT_SIIMS_final.pdf.

[12]G T赫尔曼.由投影重建图像CT的理论基础 [M].严洪范，译.北京:科学出版社,1983:1-38.

[13]赵俊红,康文雄.基于投影数据主成分分析的图像篡改检测算法 [J] .计算机工程,2012,38(10):203-205.

Zhao Jun-hong,Kang Wen-xiong.Detection algorithm of image forgery based on principal components analysis of projection data [J].Computer Engineering,2012,38(10):203-205.

[14]王敬东,徐亦斌,沈春林.一种新的任意角度旋转的景象匹配方法 [J].南京航空航天大学学报,2005,37(1):6-10.

Wang Jing-dong,Xu Yi-bin,Shen Chun-lin.New scene matching method for arbitrary rotation [J].Journal of Nanjing University of Aeronautics & Asstronautics,2005,37(1):6-10.

[15]Lin Yi-hsien,Chen Chin-hsing,Wei Chih-cheng.New method for subpixel image matching with rotation inva-riance by combining the parametric template method and the ring projection transform process [J].Optical Engineering,2006,45(6):067202/1-9.

[16]徐亦斌,王敬东,李鹏.基于圆投影向量的景象匹配方法研究 [J].系统工程与电子技术,2005,27(10):1725-1728.

Xu Yi-bin,Wang Jing-dong,Li Peng.Research on scene matching method using circular projection [J].Systems Engineering Electronics,2005,27(10):1725-1728.

Passive Forensics of Images on the Basis of ASIFT and

Circle Projection Features

ZhaoJun-hongAiWeiZhuXue-feng

(Key Laboratory of Autonomous Systems and Network Control of the Ministry of Education, South China University of Technology,

Guangzhou 510640, Guangdong, China)

Abstract:This paper deals with an image analysis method, namely passive forensics, to detect copy-move forgery, the most popular manipulation in digital tampered images. On the basis of ASIFT (Affine Scale-Invariant Feature Transform) and circle projection features, a new algorithm is proposed to detect copy-move forgery in images. The results show that the adoption of ASIFT is effective only in finding the forgery area in a tampered image with obvious corner information, while the adoption of improved circle projection features is effective only in finding the forgery area in a tampered image without such obvious corner information as random textures and flat areas. Thus, it comes to the conclusion that the combination of ASIFT and improved circle projection features is more effective for the passive forensics of copy-move forgery.

Key words： copy-move forgery; image analysis; affine scale-invariant feature transform; circle projection; passive forensics

Foundation items: Supported by the National Natural Science Foundation of China(NSFC)-Guangdong ( U1035002) and the Guangdong-Hong Kong Key Project of Science and Technology(2011A011305001,2011A011302001)

†通信作者： 胡斌杰(1960-)，男，博士，教授，主要从事无线通信天线与电波传播、射频识别等研究. E-mail: eebjiehu@scut.edu.cn