导弹弹性导向分离机构仿真分析

田 浩，李慧通，李海月

（哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001）

0 引言

导弹分离装置是导弹设计的关键部件，对导弹飞行成功至关重要［1－3］。导弹分离得到了广泛而深入的研究，目前常用的分离面纵向连接形式有螺栓式连接和包带式连接，分离过程中，连接结构解锁，利用推力和气动阻力差实现分离。上述两种连接方式，冷分离过程存在失控时间长、对另一级分离体影响大的缺点，热分离过程中需对高温燃气进行防热处理，且初始干扰大，两种分离方式均存在很大的碰撞可能性［3］。针对两种分离方式的缺点，文献［2］用柔性切割索和燃气发生器实现级间分离；文献［4-5］根据分离特点，分析了影响分离的各种参数；文献［6-7］对分离过程中分离体间的碰撞进行了判断和计算。本文对一种有导向行程长、碰撞机率大特点的套筒式导弹分离机构进行了研究。

1 分离机构组成

分离过程采用冷分离方案，用导爆索将分离连接面环向切开，反推火箭点火，将下面体推离上面体，分离过程中由安装在下面体上的8套滑轮机构进行导向和限位。导弹下面体和上面体间有较长重合段，导弹上面体安装在下面体内部，两体呈圆筒状，两组分离火箭对称安装在下面体外部，如图1所示。

图1 套筒式分离方案Fig.1 Sleeve separation scheme

滑轮机构分成上、下两组，以下面体本体坐标系为参考，上部滑轮沿坐标轴方向对称安装，下部滑轮与上部滑轮成45°角安装。滑轮组采用相同设计参数。组成导向机构的滑轮组均由弹性杆和滚轮组成，弹性杆安装在底座上，分离过程中随分离体的相对偏转而转动，从而产生压力的作用以控制两体的偏转。

2 分离模型

2.1 动力学建模

整个分离系统由上面级、下面级和8套导向滑轮机构三部分组成。简化物理模型：导向机构简化为一组末端携带滚轮的弹簧组；忽略滑轮的弹性变形；因分离高度较高，空气稀薄不考虑大气动力影响；分离时间短暂，不考虑控制伺服系统对分离的影响。分离体六自由度欧拉方程为

式中：F，m分别为分离体所受合力和质量；M为分离体所受合力矩；a为质心加速度；ω为姿态角速度；I为惯量阵。

分离体质心角速度与分离体欧拉角速度间的关系可表示为

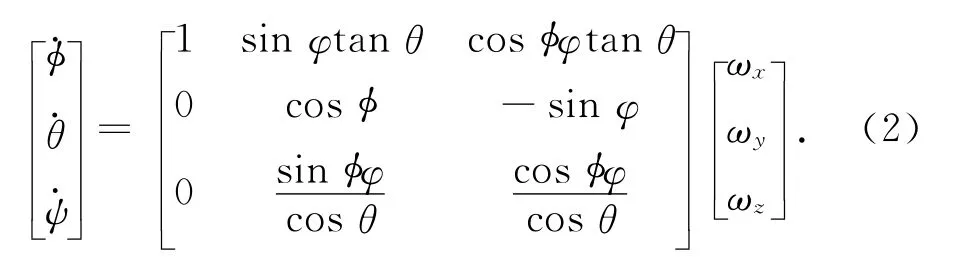
式中：x，y，z为惯性系中质心坐标位置；ωx，ωy，ωz为惯性系中质心角速度分量；φ为滚转角；θ为偏航角；ψ为俯仰角。

分离开始时刻，弹簧处于压缩状态，弹性杆刚度系数等效于弹簧弹性系数，弹性杆预压力等效于弹簧预紧力，滚轮安装高度等效于弹簧安装高度。根据两体相对姿态和相对位置计算弹性杆变形量，进而获得导向力，分离导向机构影响参数依次为刚度系数k，预紧力F0，滚轮安装高度h，导向力

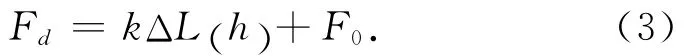
式中：ΔL（h）为弹性杆由于两体相对转动产生的变形量，姿态相同时ΔL的长度与h相关。设惯性系中上面级质心位置矢量为xac，下面级质心位置矢量xbc，安装位置相对上面级质心距离矢量为rda，弹性力作用点相对下面级质心距离矢量为rdb，则相对距离

通过惯性坐标系向弹体坐标系转换可得每个导向机构的变形量。

整个分离过程中，分离体受到反推火箭推力、导向机构导向力和拔脱机构拔脱力的作用。上面级受力和力矩分别为

式中：Fdi，Mdi分别为导向机构对分离体作用力和力矩；G为地球引力；Fc，Mc分别为低冲分离机构对分离体作用力和力矩。此处：i＝1，2，…，8。下面级受力和力矩分别为

式中：Fp，Mp分别为反推火箭对分离体作用力和力矩；Ff，Mf分别为主火箭残余推力对分离体作用力和力矩。

分离过程中分离体受到导向机构的约束力，同时受侧向力和力矩的作用，主要由反推火箭和主火箭残余推力导致。

2.2 反推火箭偏差

反推火箭残余推力点的偏差和推力方向偏斜是导致分离干扰的重要因素，对下面级弹体的姿态有重要影响，如图2所示。图中：点O为弹体质心在顶端界面的投影点。

由于质心位置与弹体中轴线并不重合，只考虑推力作用点相对质心位置的关系。

图2 火箭推力偏差Fig.2 Main engine thrust bias

反推火箭位于顶部，反推火箭的作用力随时间而变，假设某时刻反推火箭推力Fp与弹体纵轴重合，这时Fp作用在箭连体坐标系中的分量为

由于发动机推力线与火箭本体纵轴存在偏角λ，发动机推力线在火箭本体横切面上的投影与质心坐标系y轴的夹角为ρ，则发动机推力在弹体坐标系中的分量可表示为

由此得到了反推发动机对分离体侧向力偏差Y轴向大小－Fpsinλcosρ，Y轴向侧向力大小为Fpsinλsinρ。设反推火箭推力的作用点相对下面级质心的距离矢量为rp，则推力偏心产生的力矩

综上，可得反推火箭的在质心坐标系中三个轴方向的推力大小及力矩大小。

同理可得下面级主发动机残余推力的Ff，Mf。

2.3 碰撞检测

对本文研究的分离过程，碰撞问题主要考虑相互运动阶段碰撞的可能性。根据图1的分离体结构，可能发生碰撞的危险截面位置不变（如图3所示），危险截面特征点位置虽不固定，但在同一平面内变化。危险截面点位置如图3所示，分别为上面体底部圆周与下面体内部圆筒（down）和下面体顶部圆周与上面体外部圆筒（up），两位置中小间距值即为分离体最小距离。分离过程中若分离间距小于零，则表示两体发生碰撞，分离失败。

3 仿真结果

图3 分离最小间距Fig.3 Minimum distance of separation

分离体间采用套筒式安装方式，分离机构嵌套安装在下面体内圆周，两体初始距离0.1m，设定导向机构基准参数依次为k＝10kN／m，F0＝200N，h＝0.4m。分离长度到达2.5m时停止仿真。

3.1 不同间距随刚度系数时的相对姿态角

导向力与刚度系数成线性关系，仿真过程中，忽略分离体相对倾斜造成的分离不同步。预紧力和安装高度取基准参数，设定k分别为 5，8，10，15，20kN／m，对分离过程进行仿真，所得两体相对姿态角如图4～8所示。由图可知：整个仿真过程中滚转角变化幅度很小，刚度系数未对其产生明显影响；刚度系数对分离体横轴方向力矩影响较严重，故俯仰和偏航角度变化更明显。观察曲线走势可发现，小刚度系数下两体相对姿态角随时间而增大，大刚度系数下两体相对姿态角先减小后增大，这是由于刚度系数增大，两体发生偏转时由导向机构产生的恢复力矩增大，促使分离体达到一定偏转程度后发生回转。

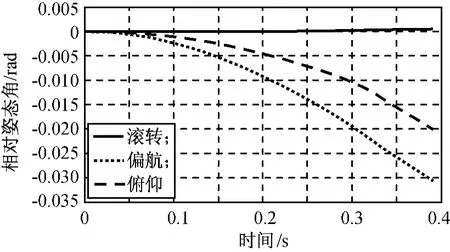
图4k＝5kN／m时两体相对姿态角Fig.4 Relative attitude fork＝5kN／m

图5k＝8kN／m时两体相对姿态角Fig.5 Relative attitude fork＝8kN／m

图6k＝10kN／m时两体相对姿态角Fig.6 Relative attitude fork＝10kN／m

图7k＝15kN／m时两体相对姿态角Fig.7 Relative attitude fork＝15kN／m

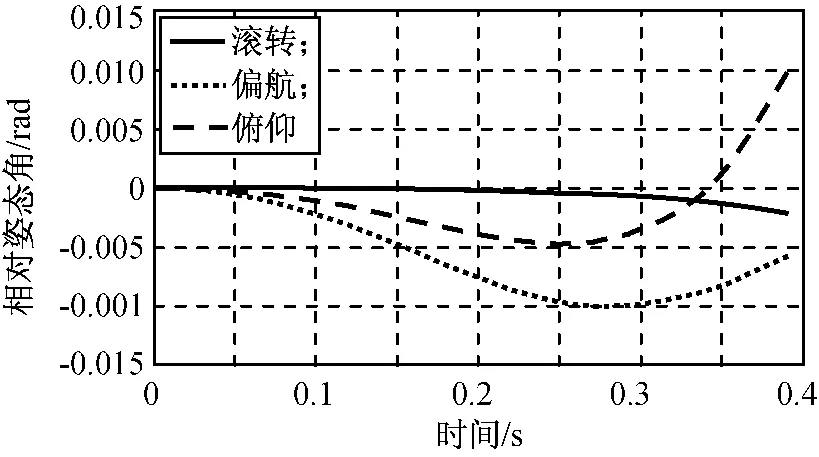
图8k＝20kN／m时两体相对姿态角Fig.8 Relative attitude fork＝20kN／m

不同刚度系数的两体最小距离仿真结果如图9所示。由图可知：刚度系数增大，两体间距先增大后减小。k＝5kN／m时，两体最小间距小于零，即两体发生碰撞，分离失败，小刚度系数不利于分离的进行。k＝16kN／m时，分离间距最大。刚度系数对姿态角的影响是形成分离距离变化规律的主要原因，小刚度系数状态下，两体相对姿态角持续增大，分离间距减小；大刚度系数下，分离后期的两体相对姿态角大幅度回转，这也造成了分离间距的减小。

图9 不同刚度系数的最小间距Fig.9 Minimum distance under various rigidity

3.2 不同预紧力时的相对姿态角与间距

一体运动阶段，导向机构处于压缩状态，具有初始预紧力，由于弹性杆不能伸长，因此当导向机构弹性杆恢复至松弛状态时，弹性力为零。刚度系数和安装高度取基准参数，设预紧力F0分别为50，100，200，500，1 000N，对分离过程进行仿真，所得两体相对姿态角如图10～14所示。由图可知：滚转角在整个分离过程中几乎接近于零，可见预紧力对其影响亦可忽略不计；F0为100，200N时，偏航角与俯仰角在分离后期有小幅回转，F0大于500N时两者持续增大。

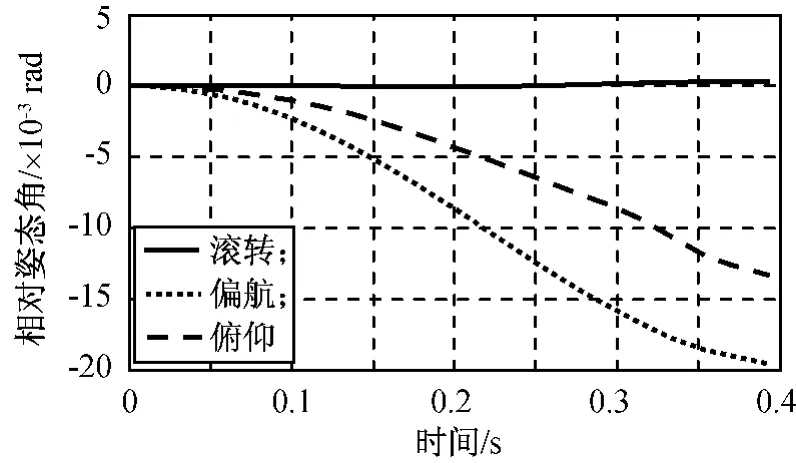
图10F0＝50N时两体相对姿态角Fig.10 Relative attitude forF0＝50N

不同预紧力时的两体最小距离仿真结果如图15所示。由图可知：F0在50～1 000N间变化时，两体最小间距先增大后减小，但间距值始终大于零，未出现碰撞现象，分离间距在预紧力为140N时达到峰值。分析预紧力对相对姿态角的影响可知，预紧力过小，上面体受导向机构作用持续偏转，偏转速度有减缓趋势，两体间距持续变小；预紧力过大，下部导向机构分离后，导向机构对下面体的力矩增大，两体偏转速率增大，两体间距迅速减小。

图11F0＝100N时两体相对姿态角Fig.11 Relative attitude forF0＝100N

图12F0＝200N时两体相对姿态角Fig.12 Relative attitude forF0＝200N

图13F0＝500N时两体相对姿态角Fig.13 Relative attitude forF0＝500N

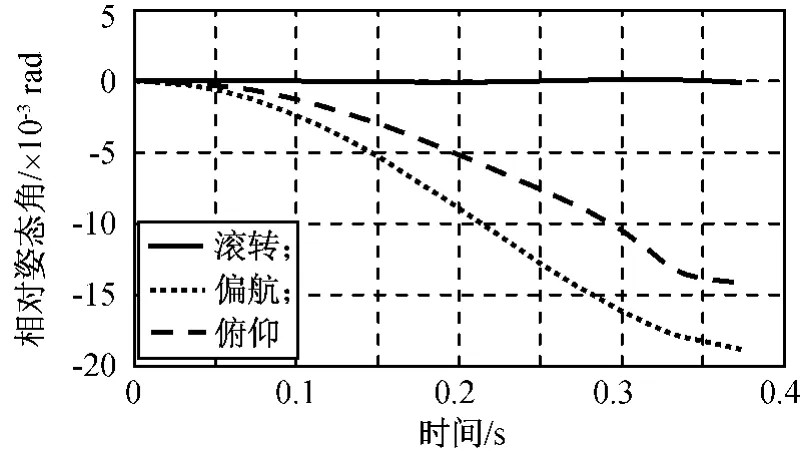
图14F0＝1 000N时两体相对姿态角Fig.14 Relative attitude forF0＝1 000N

图15 不同预紧力的最小间距Fig.15 Minimum distance under various preload

3.3 不同安装高度时的相对姿态角与间距

以组合体质心为基准平面，上、下部导向机构导向轮具有一定的安装高度，安装高度的大小影响下部导向机构分离时间和单层导向机构作用时间，进而影响分离过程中两体姿态角和间距的变化。设下面体顶部距离组合体质心高度0.7m，底部距离组合体质心1.8m，导向机构安装高度小于0.7m，刚度系数和预紧力取基准参数，在h分别为0.2，0.3，0.4，0.5，0.6m 条件下对分离过程进行仿真，所得两体相对姿态角如图16～20所示。由图可知：随着安装高度增加，俯仰角和偏航角变化幅度减小；h大于0.4m后，两者在分离后期出现拐点，且拐点时刻随高度增大而提前。

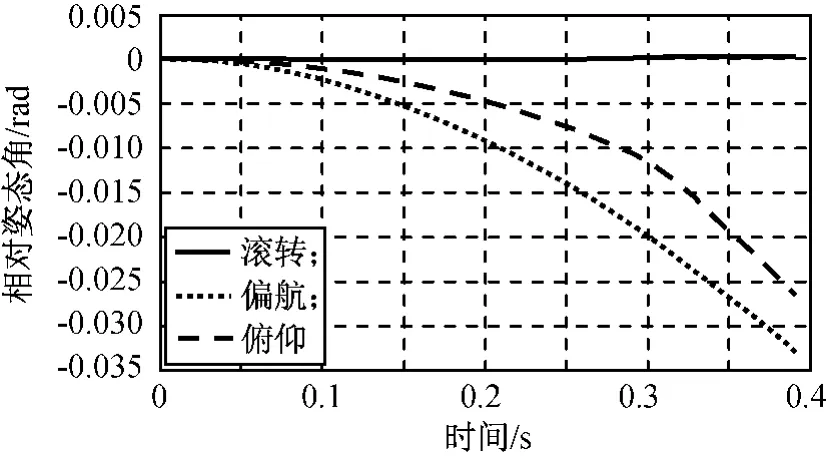
图16h＝0.2m时两体相对姿态角Fig.16 Relative attitude forh＝0.2m

不同安装高度时的两体最小距离如图21所示。由图可知：两体最小间距随h增大而增大。H为0.1，0.2m 时，两 体 最 小 距 离 分 别 为 －42.6，－7.1mm，间距小于零，分离失败，此两者安装高度不可取。受分离体结构设计限制，h不能大于0.7m，h为0.6m是仿真中的最佳分离状态。

图17h＝0.3m时两体相对姿态角Fig.17 Relative attitude forh＝0.3m

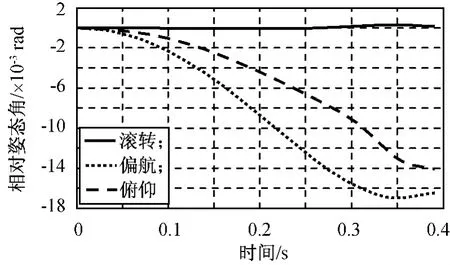
图18h＝0.4m时两体相对姿态角Fig.18 Relative attitude forh＝0.4m

图19h＝0.5m时两体相对姿态角Fig.19 Relative attitude forh＝0.5m

图20h＝0.6m时两体相对姿态角Fig.20 Relative attitude forh＝0.6m

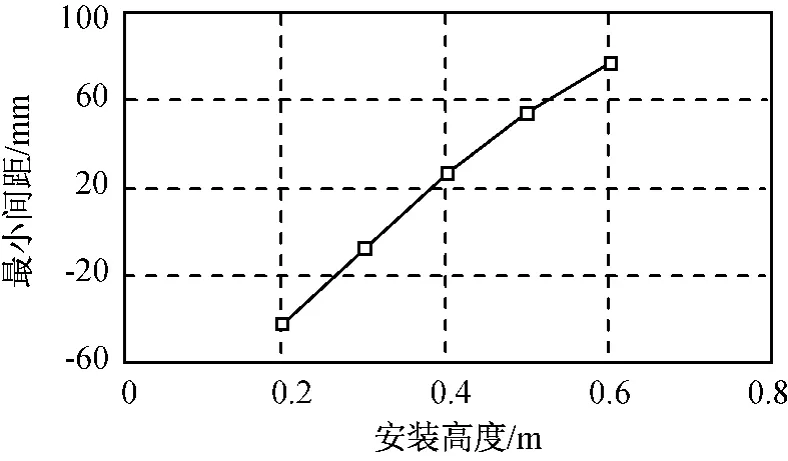
图21 不同安装高度的最小间距Fig.21 Minimum distance under various height

分析下面体力矩的变化可知：上、下部导向轮产生的作用力矩方向相反，下面体在反推火箭偏心力矩作用下发生偏转，导向力矩不断增大，下部导向轮分离后，上部导向轮力矩抑制偏转，此时若安装高度较小，则产生的抑制力矩小，不足以扭转两体相对姿态的变化趋势，若安装高度较大，其产生的力矩在某一时刻超越偏心力矩，两体姿态运动方向扭转。安装高度越大，产生力矩的力臂越大，恢复力矩超越偏心力矩时间越提前。

4 结论

针对具有导向行程长、碰撞机率大特点的分离机构，本文提出一种带弹性导向机构的分离装置，该装置能有效限制两体相对偏转，降低碰撞机率。对该导向机构参数进行了动力学建模仿真与分析，给出了分离过程中两体相对姿态与最小间距。仿真结果证明：导向机构三可变因素对分离的影响程度不同，刚度系数与安装高度对分离影响大，预紧力对分离影响较小。刚度系数增大，间距先增大后减小，间距变化范围大，小刚度系数状态下发生碰撞；间距随安装高度增大而增大，间距变化范围大，小安装高度状态下发生碰撞；预紧力增大，间距先增大后减小，间距变化范围小。由于导向机构各参数间可能存在互相影响关系，本文中各峰值参数的组合状态不一定是最佳组合参数。后续研究中，可通过比对多种组合参数的结果，以获得优化的参数组合。

［1］ 杨 涛，王中伟，张为华，等.导弹套接分离方案级间分离过程仿真分析［J］.弹箭与制导学报，2005，25（4）：144-145＋149.

［2］ 韩 松，郭凤美.一种新型级间分离技术研究［J］.宇航学报，2002，23（4）：47-51.

［3］ 朱维亮，张文峰.一种新型导弹级间分离机构研究［J］.航天返回与遥感，2005，26（1）：53-57.

［4］ 万 音.级间段气动设计及羽流诱导分离对火箭气动特性的影响［J］.宇航学报，1992，13（2）：95-98.

［5］ 任怀宇，张 铎.导弹级间热分离动态特性仿真研究［J］.宇航学报，2005，26（4）：509-513.

［6］ 张 岩，唐乾刚，张 翼，等.导弹分离碰撞判断与最小距离快速算法［J］.战术导弹技术，2003（4）：41-46.

［7］ 黄 帅，唐 硕，泮斌峰.运载火箭级间分离与碰撞检测分析［J］.科学技术与工程，2012，12（6）：1321-1324.