基于导航接收机的自旋卫星姿态确定方法

王 伟，方宝东，彭玉明

（上海卫星工程研究所，上海 200240）

0 引言

随着小卫星技术不断发展与应用，因其质量轻、体积小、成本低、发射灵活等特点而受到多个国家的重视［1］。我国某项目论证中包括两颗微小自旋卫星，若使用工程中传统的太阳－地球姿态确定方法，则需携带红外地球敏感器和太阳敏感器，不符合微小卫星轻质量、低成本的发展方向；若利用传统导航接收机确定姿态的方法，通过测量各天线对间的基线在参考坐标系中的向量表示卫星本体相对参考坐标系的姿态，则至少需要3个天线并跟踪2颗导航卫星。采用该法不仅需求解载波相位整周模糊度，而且要接收多颗卫星的信号，需用多通道处理，对接收机硬件提出了更高的要求，增加了微小卫星的重量、功耗和成本。为此，本文研究了一种基于单天线导航接收机的姿态确定方法。

1 导航接收机载波跟踪环理论

导航接收机初始捕获过程建立了对导航信号频率和代码相位参数的粗校准。导航接收机跟踪的目的是进行细调，以便系统能以精确的代码相位和频率信息解调出导航数据。因受多普勒频率、卫星频偏、采样时钟频偏等多种因素的影响，接收机须能复现导航卫星载波信号，以使其与导航卫星的信号载频相匹配。否则，在距离域内的信号相关过程将因接收机频率响应的滚降特性而出现严重衰减，使接收机不能正确捕获到卫星信号。因此，接收机先搜索导航卫星的载波多普勒频率，再跟踪该卫星的载波多普勒状态，以便在载波多普勒频域内完成载波“剥离”过程；接收机同时还须复现导航卫星发射的伪码，再移动复现码的相位，直至与卫星的伪码发生相关。码相关过程通过被相移的复现码与输入的卫星码实时相乘，由积分和累加处理而实现。当接收机复现码的相位与接收卫星码相位相匹配时，获得最大相关。当两者相位偏移超过1个基码时，得到最小相关［2－3］。码相位跟踪环和载波频率跟踪环如图1所示。图中：载波环鉴别器输出的是当前接收机环路本地载波数字控制振荡器（NCO）复现的载波相位与实际接收卫星载波相位的差值，通过对该差值进行滤波处理可算出此刻实际多普勒频率与接收机估计多普勒频率的差值，将该差值反馈至载波NCO，不断迭代完成载波信号的剥离［4］。

图1 导航接收机载波跟踪环原理Fig.1 Principle of carrier phase tracking loop of navigation receiver

2 自旋卫星姿态确定原理

对某自旋卫星，忽略空间章动因素的影响，以自旋卫星上表面中心作为坐标原点建立本体坐标系O-xbybzb（如图2所示）：卫星自旋轴方向为Ozb轴；垂直于Ozb轴的自旋卫星表面作为xbOyb平面，并在其中定义相互垂直的Oxb、Oyb轴。

图2 自旋卫星姿态测量原理Fig.2 Measuring principle of spinning satellite’s attitude

图2中：ωa为卫星自旋角速度；ra为导航接收机天线的安装半径；ρs为自旋卫星至导航卫星的距离；ψa为接收机天线与本体坐标系Oxb轴的夹角；ψs为赤道惯性坐标系中自旋卫星指向导航卫星矢量rs在xbOyb平面内的投影与Oxb轴的夹角；θs为rs与xbOyb平面的夹角。则接收机天线至导航卫星的距离

因实际有（ra／ρs）≪1，则导航接收机天线接收到的信号相位可表示为

将式（1）代入式（2），整理得

由式（4）、（5）可有

建立离散载波相位模型。设导航接收机产生的伪随机噪声码（PRN码）环开始和结束在时间节点t0，t1，t2，…，tn的载波相位模型可表示为

上述计算模型的数据来源于接收机延迟锁定环路同相信号In和正交信号Qn单位周期内的积分输出，该输出经过锁相环鉴别器得到载波相位差，即接收机跟踪环路本地生成的载波相位与实际信号载波相位的差值。锁相环鉴别器输出的载波相位差可表示为

对自旋卫星，在导航接收机跟踪环路锁定状态下，从时刻tn－1到tn的平均载波相位差可表示为

将式（8）代入式（10），整理可得

在导航接收机跟踪环路中，需通过鉴相器输出的载波相位差估计向载波NCO输入的多普勒频率ωre，且计算的ωre须使载波相位差趋向并稳定在零值附近，否则接收到的信号和本地生成信号不能很好地相关而导致接收机的跟踪环路失锁。本文采用的ωre控制率为：在时刻tn＋2预估计载波相位差等于tn时刻计算值的α倍，α为锁相环中的调节参数，为经验值，取值为0＜α≤1，本文取α＝0.92［6］。有

综上，式（11）中载波相位差yn由接收机锁相环鉴别器输出端直接获得，为已知量，由式（8）、（12）可不断计算参数xc，xs，再由式（6）、（7）计算在本体坐标系中表示自旋卫星指向导航卫星矢量s的角度θs，ψs。

导航与自旋卫星在赤道惯性坐标系中的位置信息为已知量，前者可由导航电文解算，后者可用导航星座定位确定。则自旋卫星通过导航接收机同时捕获并跟踪两颗或以上的导航卫星，用双矢量定姿技术可获得其自旋轴矢量在空间惯性坐标系中的投影，自旋卫星在空间的姿态即可确定［7－8］。

3 系统建模与仿真

3.1 系统建模与初始仿真信息

本文用仿真方法获得接收机鉴别器输出载波相位差数据，导航卫星选用美国GPS卫星导航星座。先用STK软件给出在赤道惯性坐标系内两颗导航卫星和自旋卫星的位置和速度信息，自旋卫星姿态为已知，再由卫星空间运动几何模型算出载波相位差的变化曲线。假设自旋卫星位于高度400km太阳同步轨道，且确保选择的导航卫星整个运动过程始终在接收机天线可视范围内。

仿真中，设初始参数为：ra＝0.3m；ωa＝2.09rad／s；ψa＝0°。取仿真步长为自旋卫星自旋周期的1／4；卫星自旋轴指向矢量z在赤道惯性坐标系中的投影为

令实际计算出的自旋轴指向矢量为z，z′的夹角γ表示自旋轴指向矢量计算的误差角（姿态误差角）。

3.2 仿真结果

仿真所得不同时间GPS 1，2号卫星相对自旋卫星的载波相位差如图3、4所示。

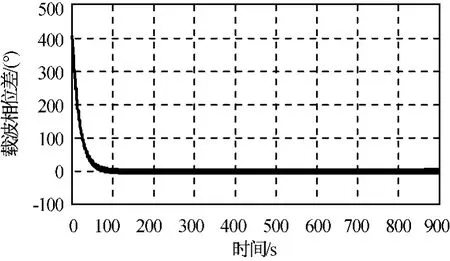
图3 GPS 1号卫星载波相位差Fig.3 Carrier phase differences of GPS 1

图4 GPS 2号卫星载波相位差Fig.4 Carrier phase differences of GPS 2

将上述载波相位差作为数据源代入仿真模型，假设载波相位差、自旋转速测量准确无误差，可得自旋卫星自旋轴指向矢量在赤道惯性坐标系中的投影分别如图5～7所示，理想状态下姿态误差角如图8所示。

图5 自旋轴指向矢量在Oxe轴上分量Fig.5 Spinning axis pointing vector onOxeaxis

图6 自旋轴指向矢量在Oye轴上分量Fig.6 Spinning axis pointing vector onOyeaxis

图7 自旋轴指向矢量在Oze轴上分量Fig.7 Spinning axis pointing vector onOzeaxis

由图5～8可知：初始时刻自旋卫星与GPS卫星载波相位差值较大，对应于接收机处于未锁定状态，载波相位差无法用于姿态确定。当接收机锁定GPS卫星信号时，载波相位差开始收敛，自旋轴矢量方向开始确定并最终稳定在理论值附近。理想状况下，实际计算值与理论值重合，误差角为零。

图8 理想状态下姿态误差角Fig.8 Attitude angle error under ideal condition

在实际的导航接收机中，载波相位的测量受射频信号干扰、卫星时钟误差、多路径偏差等因素的影响存在一定的误差。另外，自旋卫星在空间旋转过程中，自旋角速率受大气阻力、地球不规则形状引力摄动、太阳光压等因素的影响与理论转速值间也有误差。为综合考虑载波相位和自旋角速率测量误差对自旋卫星姿态确定的影响，在仿真中加入载波相位测量误差3mm的和的自旋角速率测量误差0.1（°）／s，仿真结果如图9所示。由图9可知：两种测量误差因素对定姿精度的影响约2.17°。

分别仿真载波相位误差和自旋角速率测量误差对自旋轴指向矢量误差角的影响，结果见表1。由表1可知：载波相位测量误差对定姿结果的影响较明显，是主要影响因素，自旋角速率测量误差对定姿结果的影响相对较小。根据表1给出的两种测量误差对应的误差角取值，在工程应用中可由现有的接收机和陀螺精度设备选择不同的匹配实现工程任务需求。

图9 载波相位和自旋角速率测量误差对姿态误差角的综合影响Fig.9 Influence on attitude angle error by combining carrier phase error and rotation velocity detection error

不同自旋卫星角速度ωa和接收机天线安装半径ra下的定姿精度仿真结果见表2。由表2可知：ωa的变化对自旋卫星姿态确定基本无影响，转速由10r／min提高到200r／min，误差角变化不大，其中微小的变化可能是仿真中每次加入的随机噪声值不同而造成的；ra与误差角的变化成反比，增大ra可减小误差角；载波相位和自旋角速率测量误差不变时，自旋半径从0.1m增加到5m可使误差角从6.56°减小到0.49°，因此在工程应用中应尽可能将接收机天线安装在离自旋卫星自转轴较远处，以降低对姿态确定精度的影响。

4 结束语

本文对基于导航接收机的自旋卫星的姿态确定方法进行了研究。由于采用单天线，该方法较传统导航接收机定姿的方法具有质量轻、低能耗，以及避免整周模糊度计算等优点。仿真结果表明：载波相位测量误差相对自旋角速率测量误差对姿态确定的影响是主要因素，自旋卫星角速度对姿态误差角无明显影响，接收机天线安装半径越大，姿态确定误差角越小。将上述结论用于某型号，取载波相位测量误差3mm，自旋角速率测量误差0.1（°）／s，定姿精度2.17°。

表1 不同载波相位和自旋角速率测量误差下的姿态误差角Tab.1 Attitude angle error under various carrier phase error and rotation velocity detection error

表2 不同自旋转速变化和接收机天线安装半径下的姿态误差角Tab.2 Attitude angle error under various rotation velocity variation and antenna setting radius

［1］ 罗建军，袁建平，刘祥林.卫星导航系统的发展及其军事应用［J］.全球定位系统，2001，26（1）：25-26.

［2］ KAPLAN E D，HEGARTY C J.GPS原理与应用［M］.寇艳红（译）.北京：电子工业出版社，2007.

［3］ 杨 俊.GPS基本原理及其Matlab仿真［M］.西安：西安电子科学技术出版社，2006.

［4］ 黎松友，刘良栋，严拱添.利用GPS载波相干测量技术确定空间飞行器姿态的研究［J］.控制工程，1998，1（4）：4-6.

［5］ PAOLO T.GPS based attitude determination algorithm for the spin-stabilized microsatellite UNISAT［J］.Acta Astronautica，2000，47（2）：139-146.

［6］ PSIAKI M L.Attitude sensing using aglobal-position-system antenna on a turntable［R］.AIAA，2000-3947.

［7］ 章仁为.卫星轨道姿态动力学与控制［M］.北京：航空航天大学出版社，1998.

［8］ 屠善澄.卫星姿态动力学与控制［M］.北京：宇航出版社，2001：336-339.