基于鲁棒近似方法的高超声速导弹复合控制方法研究

姚 勤，杜 英，王宇轩

（1.中国人民解放军海军驻上海地区航天系统代表室，上海 200233；2.上海航天控制技术研究所，上海 200233）

0 引言

高超声速飞行器是指飞行马赫数大于5的飞行器，被称为航空史上继发明飞机、突破声障飞行后第三个划时代的里程碑［1］。由于高超声速技术的诸多优点，高超声速导弹成为各国的研究热点。高超声速导弹具有大过载机动、适应高空复杂气动环境以及精确快速响应等特点。这些特点要求高超声速导弹飞行器控制器能有效抑制通道间的耦合和模型的参数不确定性［2－3］。传统单通道控制器无法满足高超声速导弹的控制要求。反馈线性化方法是实现非线性控制的有效方法之一，用微分几何理论抵消系统非线性项，以实现系统线性化和解耦，可用于解决高超声速导弹通道间耦合，但反馈线性化仍存在需求精确模型对不确定性敏感的缺点。目前，该领域研究主要集中于用强鲁棒的控制方法与反馈线性化结合以提高系统鲁棒性，如用模型参考自适应控制、H∞鲁棒控制等，但此类控制器结构复杂且效果不理想［4－5］。本文用鲁棒近似控制方法对补偿不确定性有强鲁棒性的优势，设计了反馈线性化和鲁棒近似复合飞行控制器并进行仿真验证。

1 被控对象模型

1.1 弹体动力学模型

由动力学、运动学方程可得高超声速导弹三通道多输入多输出非线性模型

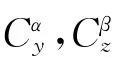
1.2 弹体系过载模型

高超声速导弹在弹体系中的过载完整模型可表示为

式中：X为速度方向空气阻力；ny，nz分别为俯仰和偏航方向过载。

2 控制器设计

2.1 反馈线性化

将滚动通道的斜吹力矩作为干扰处理。由式（1）可知，滚动通道不受其他两个通道的耦合影响，可进行单通道设计。针对俯仰通道、偏航通道的耦合模型应用反馈线性化方法进行精确线性化变换。

取俯仰、偏航通道中的状态变量为［α ωzβωy］T，控制量为 ［δzδy］T，变化后的仿射非线性系统为

滚动通道的模型不变，仍为

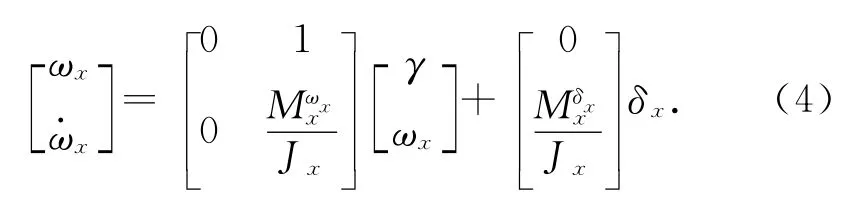
对俯仰／偏航通道二输入二输出非线性耦合系统使用反馈线性化解耦。经L导数变换得判别矩阵为

1（x）≠0Lfh2（x）≠0，得相对阶ρ＝ （r1，r2）＝ （2，2），满足线性化要求r1＋r2＝4＝n。由此可得结论：原非线性系统可通过反馈线性化完全解耦。

E非奇异，则可取控制量

将控制量代入原方程式（3）进行反馈线性化，则俯仰／偏航通道模型分别为

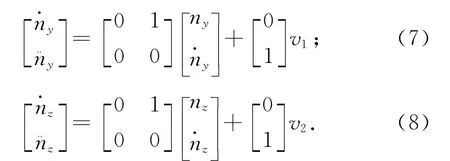
2.2 鲁棒近似控制器

针对模型式（7）、（8）设计鲁棒近似控制器，实现鲁棒近似与反馈线性化复合控制，提高控制系统的鲁棒性。鲁棒近似控制的优点是：在抵消系统非线性动态的同时，自动估计并补偿了系统的各种不确定因素和未知因素，适应性和鲁棒性很强；需要整定的参数少，并有明确的物理意义作指导；不依赖于被控对象的具体表达形式，对模型信息的需求量少，结构简单且原理直观清晰，为工程应用提供了方便。

图1 鲁棒近似控制器结构原理Fig.1 Configuration of the bust approximate method

2.2.1 鲁棒近似控制理论基础

基于反馈线性化，根据式（6）定义新状态变量

式中：a（z，w）为E中元素。式（9）中包含了模型的所有信息，可视为系统的一维扩张状态，则

若控制对象模型出现参数摄动，则经反馈线性化后的线性模型中将出现偏差量。由于反馈线性化运算复杂，包含求解偏导、矩阵求逆等运算，偏差量具体形式无法得知，一般只能得到偏差量的近似表达式，无法实现对偏差量的完全补偿，导致控制性能下降。因此，期望用一种性能优越的观测器，对包含系统非线性动态、模型不确定性及外部干扰等所有不确定性干扰量的扩张状态d（z，w，u）进行估计和补偿。

假设模型扩张变量的导数（z，w，u）有界。依据具体对象模型的特点及控制跟踪要求，特别是相对阶ρ的值，构造一种简单易实现的观测器结构。通过观测对象模型的输入输出值，实时得到对象模型的动态估计状态量，从而对不确定对象的总体状态进行完全补偿。与一般观测器不同的是，所观测的不是某个或数个单独的状态变量，而是包含完整模型动态特性的扩张状态。观测器结构会产生积分作用，可消除阶跃响应下的稳态误差，实现对控制指令精确跟踪。

状态调节器的模型观测器结构为

式 中：ξ为 定 义 的 中 间 变 量；kρ－1＝sgn （b（z，w））μ；ki（i＝0，…，ρ－2） 为任意常数，会一定程度影响系统动态性能［6］。此处：μ为某一适当的正数，此系数决定闭环系统的稳定性。

鲁棒近似反馈线性化的控制律为

考虑式（10）、（12），得到

式中：为模型观测器产生的估计误差，且＝d－。只要有界且值足够小，系统仍可近似为线性的积分串联型

2.2.2 设计步骤

对模型（7）、（8）设计鲁棒近似控制器，步骤如下：

a）由模型对象可知误差导数（z，w，u）有界，满足鲁棒近似的要求。

b）与状态反馈一样选取满足性能指标的极点，经调试选择状态极点为（－6＋3i，－6－3i）。此处：i为虚数单位。

c）用式（3）设计扩张观测器，可得

设 计 控 制 器 中 参 数，其 中h1，h2满 足（s＋6＋3i）（s＋6 －3i）＝s2＋h2s＋h1。取k1＝5，k2＝5。

根据以上步骤，可得到鲁棒近似控制器，将其用于反馈线性化后的模型，实现与反馈线性化复合控制。

3 仿真验证

建立导弹的非线性刚体动力学模型，对所设计的反馈线性化控制律进行仿真验证。设模型参数：马赫数Ma＝5，高度H＝22km。取仿真初值为：α0＝0°，β0＝0°，ωz0＝0（°）／s，ωy0＝0（°）／s，δy0＝0°，δz0＝0°。仿真条件为：在2s时刻分别加入滚动干扰50（°）／s；对标称参数进行2.0，0.5倍拉偏，仿真结果如图2所示。

图2 过载响应Fig.2 Response ofg-control

由仿真结果可知：在反馈线性化作用下，滚动引起的俯仰、偏航通道耦合作用被有效抑制。同时使用鲁棒近似控制后，控制对象模型参数发生较大摄动时，仍能有效地进行控制并且无稳态误差，设计的控制系统有较强的鲁棒性。

4 结束语

本文用反馈线性化和鲁棒近似复合控制方法设计了高超声速导弹的飞行器控制器。用反馈线性化对通道耦合的非线性导弹模型进行控制器设计，实现对导弹俯仰／偏航通道的过载控制。针对反馈线性化方法模型精确性敏感问题，结合鲁棒近似控制方法，有效提高了飞行器控制器的鲁棒性。仿真结果表明本文设计的控制器可有效抑制通道耦合且有较强鲁棒性。

［1］ 黄 琳，段志生，杨剑影.近空间高超声速飞行器对控制科学的挑战［J］.控制理论与应用，2011，28（10）：1496.

［2］ NIELSEN J N.Nonlinearities in missile aerodynamics［R］.AIAA，1987-78-20.

［3］ 李丽娜，杨 军.大攻角飞行导弹自动驾驶仪反馈线性化设计［J］.火力与指挥控制，2009（3）：113-115.

［4］ 孙兆兴.高超声声速导弹复合控制方法［D］.哈尔滨：哈尔滨工业大学，2011.

［5］ MARRISON C I，STENGEl R F.Design of robust control systems for a hypersonic aircraft［J］.AIAA Journal of Guidance，Control，and Dynamics，1998，21（1）：58-63.

［6］ 陈金莉.鲁棒近似反馈线性化方法及其在航天器姿态控制中的应用［D］.北京：北京航空航天大学，2007.