转台伺服系统的动态滑模控制研究

陈 坤，闵 斌，于启洋，张 垚

（1.上海航天控制技术研究所，上海 200233；2.山东信息通信技术研究院，山东 济南 250101）

0 引言

近年来，随着航空、航天技术的发展，各种高精度飞行器获得了大力发展。作为仿真及测试与分析试验的平台，对转台的相应性能要求也越来越高，这些性能要求包括超低速、高精度、宽调速、高频响等。长期以来，传统PID控制在伺服控制领域被广泛应用，但该控制策略很难处理系统不确定性的影响。在实际转台控制系统中，因各种因素的影响，使转台控制系统中存在非线性因素：摩擦力矩、干扰力矩、耦合力矩等多个不确定项，如转动惯量（源自负载变化）等参数变化；高频未建模动态及机械谐振；测量延时及测量噪声［1］。由于上述因素的存在，无法建立精确的数学模型，如忽略对象的不确定性，根据近似或简化模型设计控制器，被忽略的因素可能会引起控制系统品质的恶化，甚至导致系统的不稳定。因滑模变结构控制对外部干扰和不确定性具强鲁棒特性，故可基于滑模变结构控制理论，设计动态滑模控制器，以提高转台控制中的抗干扰性［2－3］。对常规滑模控制器，其最大缺点是抖振明显，可引入动态滑模控制器以削弱传统滑模控制带来的抖振。本文对转台伺服系统的动态滑模控制进行了研究。

1 转台伺服系统模型

在控制系统设计中，需先解决控制对象的数学建模。本文研究的转台控制系统由三个独立通道组成，控制结构基本相同，在正常情况下其中任意框的模型可简化为线性二阶环节系统。该系统采用直流力矩电机驱动，忽略电枢电感影响。DSMC结构如图1所示。图中：Kpu为功放增益；Km为转矩系数；Ke为反电动势系数；J为转动惯量；Df为干扰力矩；Ra为电枢电阻；Θ（s），Ω（s）分别为角位置θ与角速度的拉氏变换。

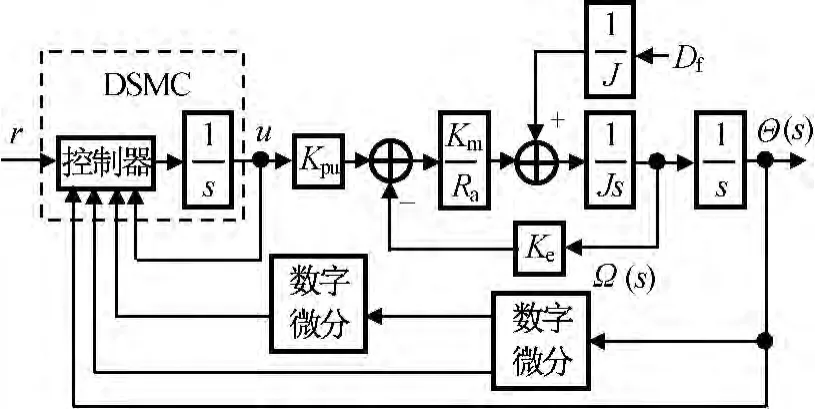
图1 DSMC转台伺服系统结构Fig.1 Strueture of DSMC tumate servo system

对图1所示的系统，其状态方程可表示为

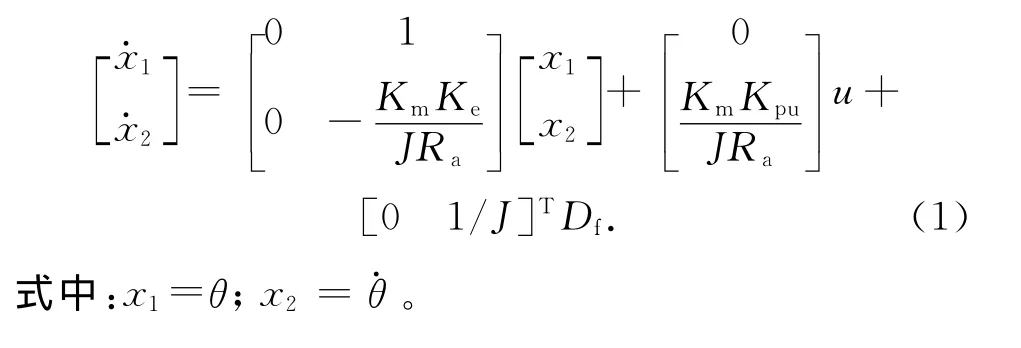
2 动态滑模控制

动态滑模方法是将常规滑模变结构控制中的切换函数s通过微分环节构成新的切换函数δ，该切换函数与控制器输出的一阶或高阶导数有关，可将不连续项转移至控制的一阶或高阶导数中，得到在时间上本质连续的动态滑模控制律，有效削弱抖振。

2.1 控制器设计

设跟踪误差

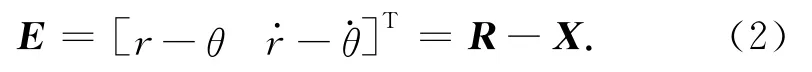
式中：r为位置指令；R＝ ［］T；X＝ ［x1x2］T＝［］T。

定义切换函数

式中：D为大于0的常数；C＝［c1c2］；u为控制量。当s＝0时，Du＝－CE。为形成负反馈，要求C＜0。则切换函数的一阶导数

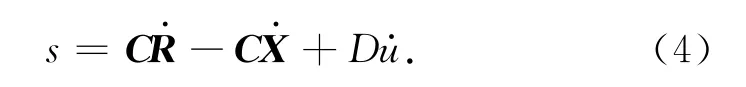
采用指数趋近律

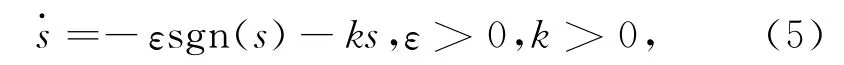
则由式（4）、（5）可得动态控制律

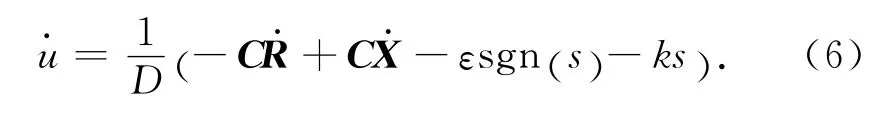
2.2 稳定性分析

定义Lyapunov函数V＝0.5s2，则

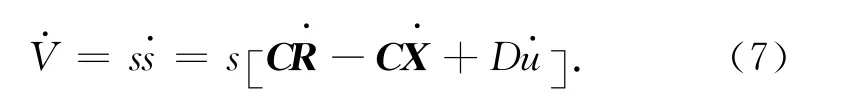
将式（6）代入式（8）可得

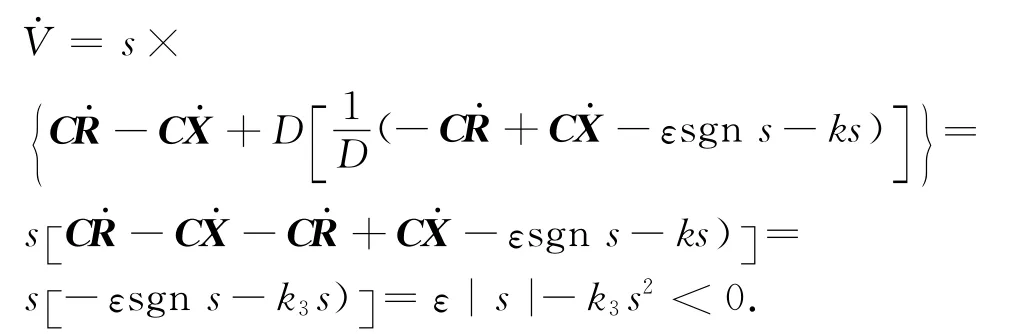
故本文设计的动态滑模控制律Lyapunov稳定。

3 仿真

本文某三轴转台中的一个框架为例，在Simulink软件中搭建相关模型。取系统模型：Ra＝6.3Ω，Ke＝6V／（rad·s－1），Km＝3.8N·m／A，J＝0.9kg·m2。 动 态 滑 模 控 制 律 中，取C＝－［300 0.095］，D＝0.003，ε＝0.1，k＝20。取位置参考输入信号r（t）＝0.001sin（4πt），外加干扰力矩Df＝5sin（20πt）。仿真结果如图2～3所示。

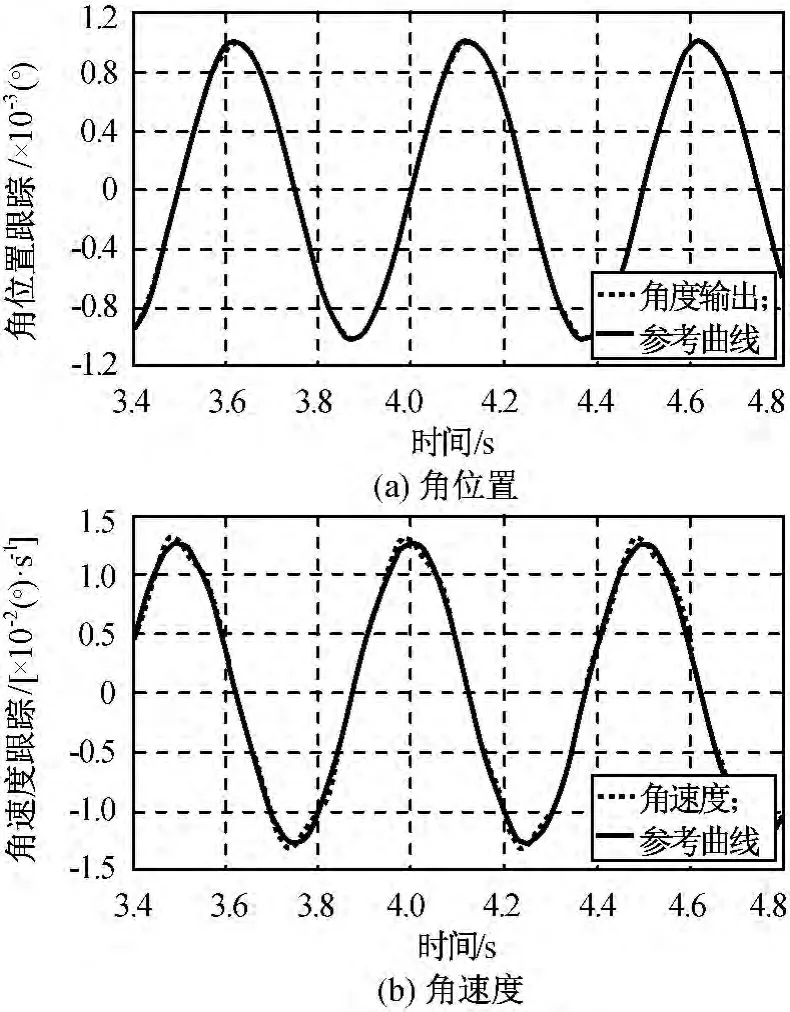
图2 PID跟踪结果Fig.2 Tracing result of PID

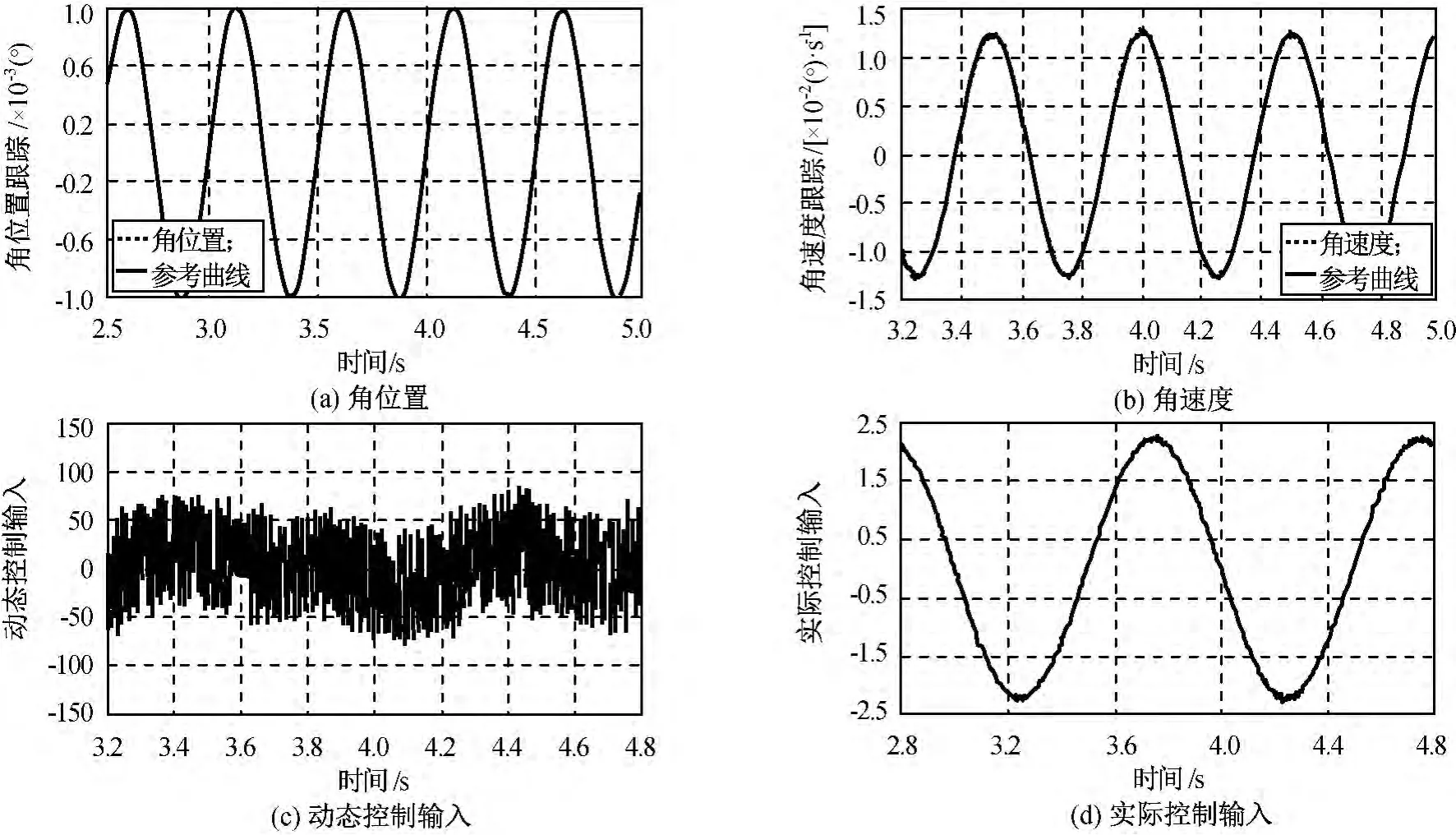
图3 DSMC跟踪结果Fig.3 Tracing result of DSMC

比较图2、3可知：采用DSMC，角度输出和角速度输出能更好地跟踪相应的参考输入曲线，表明DSMC能更有效抑制干扰力矩，鲁棒性更强。由图3（c）、（d）可知：动态控制输入信号u·抖动较大，其中包含很多不连续信号，经将系统控制输入的一阶导数引入切换函数，得到的实际系统控制输入信号，实现了在时间上本质连续的动态滑模控制律，有效降低了抖振。

为进一步证明DSMC削弱抖振的作用，采用基于指数趋近律的传统滑模控制（SMC），并用极点配置法求切换函数，控制器参数：ε＝0.1，k＝20，c1＝6，c2＝0.1［4］。仿真结果如图4、5所示。

比较图3（b）、图4（b）可知：DSMC的角速度跟踪曲线的抖振程度稍小。比较图3（d）、图5可知：SMC的控制输入抖动严重，而DSMC则明显更好，进一步证明了DSMC的优越性。

4 结束语

针对转台控制系统中的各种不确定因素的影响，如高频力矩干扰，为提高系统的鲁棒性，本文采用动态滑模控制方法，根据滑模控制理论并进行MATLAB仿真，结果表明，与传统双闭环PID控制相比，DSMC具有更强的鲁棒性。与传统滑模控制（SMC）相比，DSMC有更平滑更连续的控制输入，并在一定程度上削弱抖振。

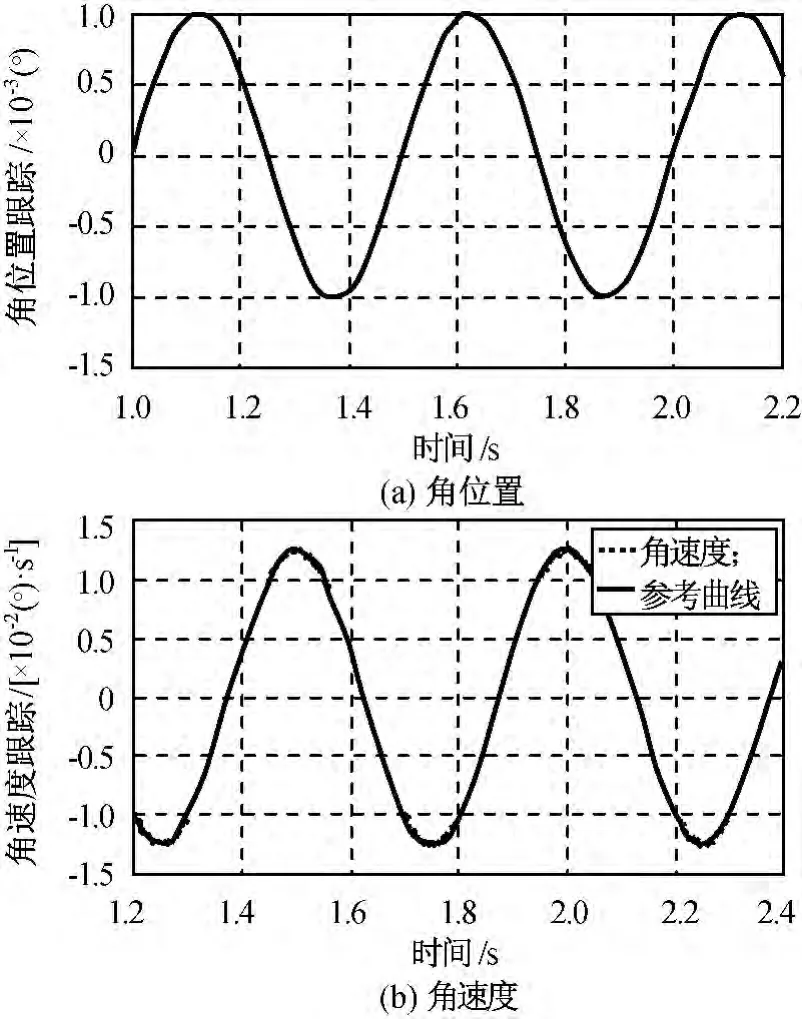
图4 SMC跟踪结果Fig.4 Tracing result of SMC

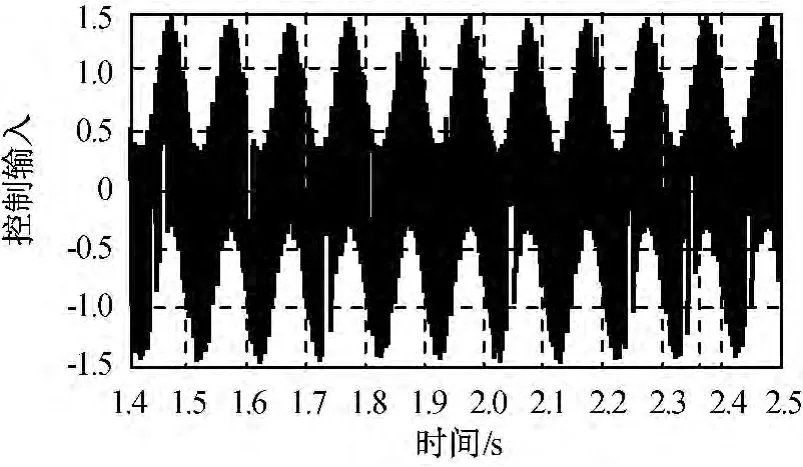
图5 SMC控制输入信号Fig.5 Input signal of SMC control

［1］ 刘金琨.滑模变结构控制 MATLAB仿真［M］.北京：清华大学出版社，2005.

［2］ PIEPER J.First order dynamic sliding mode control［C］／／ Proceedings of the 37thIEEE Conference on Decision ＆ Control.Tampa：IEEE，1998：2415-2420.

［3］ RAMIREZ H S，SANTIAGO O L.Adaptive dynamic sliding mode control via backstepping［C］／／Proceedings of the 32thIEEE Conference on Decision ＆Control.San Antonia：IEEE，1992：1422-1427.

［4］ 胡跃明.变结构控制理论与应用［M］.北京：科学出版社，2003.