基于CORDIC算法的半球谐振陀螺信号相位跟踪和解调

夏 语，李建勋，张明举，赵万良，王 伟

（1.上海交通大学 机械与动力工程学院，上海 200240；2.上海航天控制技术研究所，上海 200233）

0 引言

半球谐振陀螺是新一代惯性敏感元件，其机械结构中无经典陀螺中的高速转子和活动支承，利用半球谐振子产生的哥氏效应引起振型移动实现角度或角速率的测量，寿命可达15年以上，具有测量精度高、稳定性强、抗辐射、长寿命等优点，特别适于空间领域应用。从1996年NASA将第一颗装有半球谐振陀螺空间惯性参考单元的卫星送上太空至今，美国在轨工作的半球谐振陀螺惯性基准已有91套，累计工作时间超过1 200万小时，在轨工作无一失效［1］。近年来，我国自主研发的半球谐振陀螺惯性基准也取得了较大的进展［2］。2012年10月发射的实践9号卫星首次搭载了中国电科26所研制的半球谐振陀螺惯性组合，成功切入卫星姿态控制系统，参与卫星姿态控制，在轨运行稳定，但其精度较国外产品差距较大［3］。国内的半球谐振陀螺控制回路主要以模拟电路为主，回路中相位跟踪器用锁相环的方式实现，锁相环电路由压控振荡器（VCO）和锁相回路（PLL）组成，VCO输出的信号分成两路，一路通过分频和锁相回路产生本振信号，另一路信号与本振信号相位比较，若相位差为定值，则说明相位已被跟踪，若相位差在变化，则锁相回路输出将变化，控制VCO，使相位差稳定，说明锁相环的输入与输出频率与相位保持特定关系，完成锁相的闭环。但模拟电路用于陀螺控制回路中缺点有：模拟器件温度偏移较严重，温度变化时参数会随之改变，影响陀螺性能稳定；模拟电路各模块易引入噪声，前后器件会互相影响，调试过程复杂；性能优良的模拟电路滤波器设计复杂，阶数一般较高，占用印制板面积大。数字电路精度高、可靠性强、设计简便、受温度影响小，非常适于陀螺控制回路。数字控制回路中，用现场可编程逻辑阵列（FPGA）或数字信号处理器（DSP）为基础，设计相位跟踪器中采用直接数字频率合成（DDS）技术。以查找表为核心的相位跟踪器虽然原理简单，但实现较困难，以CORDIC算法为核心的相位跟踪器易实现，且能同时完成陀螺信号解调任务。为此，本文研究了两种基于FPGA的HRG的相位和解调。

1 HRG螺数字控制回路原理介绍

HRG数字控制回路从陀螺的读出电极获取x、y两路输入信号，经A／D采样，进入FPGA完成相位跟踪和三路信号处理，信号处理过程分为解调、低通滤波、PID控制和调制，通过执行机构作用于陀螺。其原理如图1所示。

相位跟踪器是回路中重要组成部分。它通过两次过零信号的间隔估计载波频率，并计算出对应的相位累加步进，再进行步进累加，最后输出与输入信号相位相同的本地载波。本地载波的精度直接关系解调陀螺信号和调制信号的精度，当本地载波精度不足时，会造成整个系统性能下降。因此，相位跟踪器设计尤为重要，一种以查找表法为核心相位跟踪器如图2所示。

图1 HRG数字控制回路Fig.1 Digital control loop of HRG

图2 以查找表法为核心的相位跟踪器Fig.2 Phase tracker based on lookup table

过零比较信号由计数器得到计数N，利用360／N模块得到360°与N的商，即相位累加步进Cp。Cp自身累加后得到所需的正余弦地址，然后在SRAM中的查找表中读取对应的正余弦值，即生成本地载波Vrc，Vrs并送回FPGA。通过计算得出查找表需约16MB储存空间，该查找表无法置于FPGA中，只能存放于SRAM中。此外还需增加FLASH芯片，用于断电储存查找表。

该方案的特点是：软件需增加FPGA与SRAM、FLASH的通信模块程序；读写SRAM需消耗一定的FPGA资源；硬件需增加FLASH和SRAM等芯片，这增加了印制板面积，增加了未来HRG惯性组合小型化的难度。因此，有必要更换低硬件复杂度、低资源消耗的方案。

本文利用CORDIC算法特点，设计了一种算法简单、无需增加硬件的相位跟踪器，且跟踪器可在生成本地载波同时完成陀螺信号的解调任务，极大节约FPGA资源。

2 基于CORDIC算法的相位跟踪器方案设计

CORDIC算法即坐标旋转数字计算方法，该算法通过多次迭代加法和移位运算产生高精度的正余弦波形。

已知向量（xi，yi），以及旋转量θi，可计算出旋转后的向量值（xi＋1，yi＋1），有

式中：0≤i≤n。此处：n为迭代次数。n越大，xn，yn就越逼近真实目标值。

用于CORDIC算法中每个迭代i的旋转角度见表1。

表1 迭代旋转角度Tab.1 Iterative rotation angle

提取cosθi，将tanθi＝2－i代入式（1），可得

式（2）中：2－i在二进制中实际操作为小数点向右移动i位，以此可证明CORDIC算法仅需简单的移位和相加运算就能进行三角运算；zi用于累加每次迭代过程中追踪累加的旋转角度，迭代i次后zi将逼近于0，而xi，yi将逼近真实的目标值；di为±1，由zi的符号位决定，当zi＜0时，di＝1，否则为－1。

CORDIC算法基本逻辑如图3所示。

由以上CORDIC算法原理可实现相位跟踪器功能。对CORDIC逻辑模块，式（1）累加n次后得

式中：K为在迭代n次后xn，yn的被伸缩倍数（即每个迭代方程中cosθi的积），且

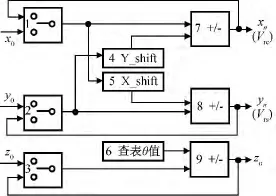
图3 CORDIC算法基本逻辑Fig.3 CORDIC algorithm basic logic

故当x0＝K，y0＝0，z0为控制回路中的相位累加值时，由式（3）可得本地载波

以CORDIC算法为核心的相位跟踪器原理如图4所示。以CORDIC算法为核心的相位跟踪器能在FPGA中完成所有的本地载波生成任务，无需与SRAM通信读写外置查找表，且算法中只有加法和移位，消耗资源少并能减少系统延时。

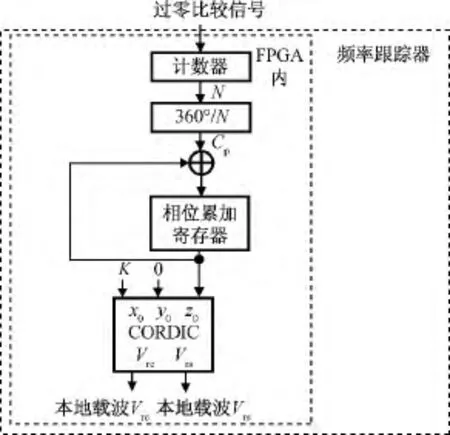
图4 以CORDIC算法为核心的相位跟踪器Fig.4 Phase tracker based on CORDIC algorithm

3 用CORDIC逻辑模块完成信号解调

传统半球谐振陀螺信号解调方案是：相位跟踪器生成的本地载波Vrc，Vrs与x，y相乘进行解调，需要3个乘法器解调出3路控制信号，如图5所示。

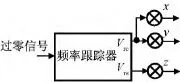
图5 信号解调Fig.5 Signal demodulation

以CORDIC算法为核心的相位跟踪器除能便利地得到本地载波外，还可利用其原理完成控制回路中的解调过程（如图6所示），能节约3个乘法运算。

以x线路为例，令式（5）的初始值：x0为输入陀螺信号x，y0＝0，z0为相位累加值，则

由此可见，可通过CORDIC自身算法直接输出x、y信号与本地载波的乘积，完成3路信号的解调，节省3个乘法器，且整个系统的输出也无变化。用CORDIC解调后的数字控制回路如图7所示。

图6 用CORDIC内部逻辑完成信号解调过程Fig.6 Signal demodulate process with CORDIC logic

4 方案仿真验证

分别对以查找表法为核心的相位跟踪器及解调过程（A方案，如图8所示）和以CORDIC算法为核心的相位跟踪器及解调过程（B方案，如图9所示）进行建模（两个方案的输出均通过低通滤波器，否则信号会被高频淹没）。

图7 CORDIC解调的数字控制回路Fig.7 Digital control loop with CORDIC demodulation

图8 查找表法为核心的相位跟踪器及解调过程（方案A）Fig.8 Phase tracker and demodulation based on lookup table（scheme A）

图9 CORDIC逻辑为核心的相位跟踪器及解调过程（方案B）Fig.9 Phase tracker and demodulation based on CORDIC algorithm （scheme B）

仿真条件如下：仿真输入（模拟过零比较信号）4.5kHz方波信号，高电平＋1V，低电平0V，占空比50%；仿真输出幅值控制解调信号xVrc，力反馈控制解调信号yVrc，正交控制解调信号yVrs。

4.1 仿真结果对比

方案A、B分别在Simulink中进行仿真，结果如图10～12所示。由图可知：初始化期间（前0.4×10－3s内）波形不同，0.4×10－3s后波形相同（严格说两波形是倍数关系，该倍数与上文推算的伸缩因子K≈0.607 3相同），而K可在之后的PID环节吸收，故方案B可从功能和性能上替代方案A。

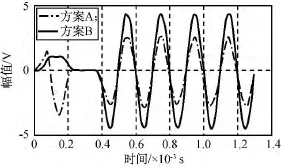
图10 两种方案幅值解调信号（xVrc）输出Fig.10 Amplitude demodulation signal output of two schemes

4.2 FPGA资源评估

宇航级的FPGA的逻辑单元仅为工业级的FPGA约1／10倍，节约FPGA资源对航天产品是必须考虑的。评估FPGA资源使用率时，选用的是ANTEL的型号为A3P250FPGA，该FPGA有逻辑单元25万门，用Modelsim对方案A、B对应的Verilog程序进行评估。方案A资源利用率可达128.91%，已超出硬件的极限，方案B资源利用率为80.47%，方案B较方案A少3个乘法器，节约FPGA资源近50%。

图11 两种方案力反馈解调信号（yVrc）输出Fig.11 Force feedback demodulation signal output of two schemes

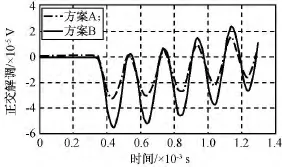
图12 两种方案正交解调信号（yVrs）输出Fig.12 Quadrature demodulation signal output of two schemes

以上算法验证和仿真结果表明，方案A、B的输出结果完全一致，但方案B的软件减少了通信模块，硬件减少了SRAM，FLASH，并可节约大量的FPGA资源。由此可认为以CORDIC算法为核心的相位跟踪器更优。

5 结束语

本文设计了半球谐振陀螺数字控制回路中两种相位跟踪器。与以查找表法为核心的相位跟踪器相比，以CORDIC算法为核心的相位跟踪器只用加法和移位实现了相位跟踪和陀螺信号解调的功能，其软硬件实现简单、计算快速、节约资源，算法推算和仿真试验结果表明该法的可靠性高，能保证整个回路的数据精度要求。本文研究为陀螺数字信号系统的设计提供了一定的参考依据。

［1］ ROZELLE D M.The hemispherical resonator gyro：from wineglass to the planets［R］.Northrop Grumman Corporation，2004.

［2］ 高胜利.半球谐振陀螺的分析与设计［D］.哈尔滨：哈尔滨工程大学，2008.

［3］ 中国电子科技集团公司.中国电科研制的半球谐振陀螺完成卫星闭环控制试验［EB／R］.［2012－12－21］.http：／／www.sasac.gov.cn／n1180／n1226／n2410／n314319／15024297.html.