库仑力卫星编队动力学建模及基本稳定条件分析

孙 杰，张东青，张红英，张锦绣

（1.上海卫星工程研究所，上海 200240；2.哈尔滨工业大学 卫星技术研究所，黑龙江 哈尔滨 150080）

0 引言

自20世纪90年代以来，卫星编队飞行技术得到了迅速发展，美、俄、欧空局等众多国家和空间组织机构都开展了编队飞行技术的研究，并取得了卓越的成效，尤其是由DLR研制的TanDEM-X编队在2010年7月投入运行，该计划是国际上首个投入在轨运行的近地卫星编队［1］。随着技术的发展和任务的不同，对近距离编队甚至超近距离编队也提出了技术需求。

库仑力卫星编队技术是近年来一种新兴的编队技术［2］，其基本概念是采用一定技术手段（如电子枪）使卫星带电（正电荷或负电荷），通过控制卫星带电量实现卫星编队相对位置的控制，未来将成为解决超近距离编队的一种有效途径。在库仑力卫星编队中，任意两颗卫星间的相对距离由它们间的库仑力控制，故不会产生对邻近卫星敏感器的污染问题；同样，基于带同性电荷卫星相互排斥机理，在近距离编队时带同性电荷的卫星也不会产生碰撞问题。因此，库仑力编队既可利用卫星在空间环境中充电的特性产生控制力，又能解决现有推进系统的敏感器污染和近距离碰撞问题。前期空间试验已经证明了空间环境中卫星表面带电的可能性，对电磁力卫星编队也进行了大量的研究。1979年发射的史卡莎（SCATHA）试验卫星表明在空间等离子环境中仅数十毫安的电流就可使卫星获得3kV电势，空间等离子环境可充电势达14kV，且基于库仑力控制比冲可达1 000ms，远高于 EP推力器［3－4］。文献［5］建立了N体充电卫星的动力学模型，其主要基于圆轨道假设，且成员间的距离小于100m；文献［6］研究了两卫星间利用库仑力系绳编队的动力学方程及其稳定性问题；文献［7］讨论了几种稳定的编队构形，并提出了一些关于闭环控制的问题；文献［8］提出了表明基于库仑力实现系统编队重构的方法以节约能量。

本文对库仑力卫星编队空间德拜屏蔽效应进行了分析，用拉格朗日方程建立了Hill坐标系中的地球同步轨道库仑力编队相对运动动力学模型，分析了系统的基本平衡条件，并用于地球同步轨道上的两星编队。

1 参考坐标系

2 库仑力编队空间德拜屏蔽效应

在包括大气阻力、地球非球形摄动、太阳光压、空间等离子等多个影响库伦力编队性能的因素中，空间等离子环境直接影响库仑力编队的性能，其中最突出的因素为德拜（Debye）屏蔽效应［9］。德拜屏蔽效应的分析结果将直接决定库伦力编队的应用范围。

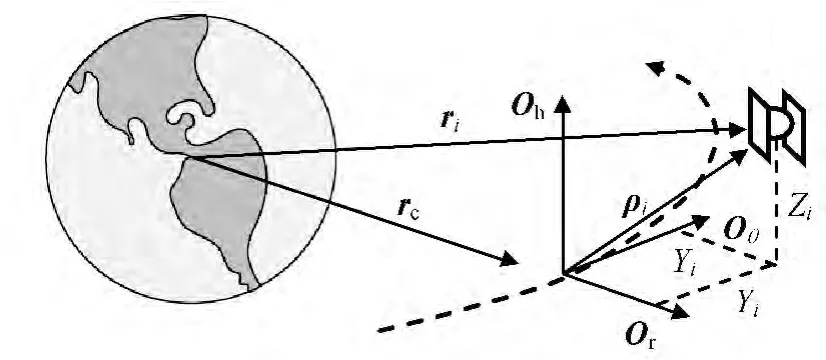
图1 Hill坐标系Fig.1 Hill coordinate

由静电学理论可知，带电体在等离子和真空环境中的表现完全不同。将一正电荷放入等离子环境中，它将吸引等离子环境中的负电荷，同时排斥等离子环境中的正电荷，最终会成一个负电荷团，将该正电荷包围，并屏蔽这个正电荷的电场。因此，电场在等离子环境中衰减较在真空中更快，该现象被称为德拜屏蔽效应，电荷团的平均半径称为德拜长度。

当与正电荷的距离大于德拜长度时，正电荷的电场呈指数衰减，可表示为

式中：F为库仑力；kc为静电引力常数；q为星体带电量；d为星体间距；λd为德拜长度。当与正电荷的距离小于德拜长度时，正电荷的电场相当于一个点电荷在真空中的电场。

在不同的轨道高度，因环境中离子密度不同，德拜长度有所差异。同时，太阳的活动对德拜长度也有一定影响。不同轨道高度德拜长度见表1［10］。

表1 不同高度轨道的德拜长度值Tab.1 Debye length at different orbit

由表1可知：在近地轨道，德拜长度仅为2～40cm，要求编队的距离极小，仅适于卫星机构的对接操作，不适于进行编队飞行；在地球同步轨道，德拜长度为100～1 000m量级，完全能满足编队飞行的需要；对深空环境，库仑力编队也具备一定前景，但仅限较近距离编队飞行。本文选择地球同步轨道对库仑力编队进行动力学建模与稳定性分析。

3 库仑力编队动力学建模

为便于分析问题，将Hill模型的原点建立在编队质心处。则在编队质心处式成立

式中：xcm，zcm为库仑力编队在Hill模型中的质心位置坐标；n为轨道角速度［11］。可见，若xcm，zcm为零，则卫星编队质心在X、Z向上无加速度，编队达到稳定状态，同时卫星编队质心在Y向上有位移但对编队稳定性无影响。为使卫星编队在初始时刻就达到稳定和编队的唯一性，令卫星在Y向上无初始位移，即成立质心条件

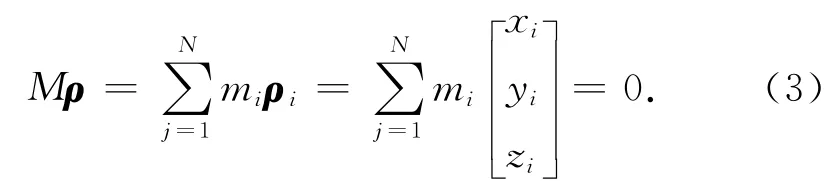
式中：M为卫星编队的质心；ρi为卫星编队质心在Hill模型中的位置矢量；xi，yi，zi分别为ρ的三轴标量。

进一步为克服重力梯度力矩，编队系统一个惯性主轴须沿向；为保证编队绕地球的角速度，编队一个惯性主轴须与轴重合；第三个主轴的方向由右手定则自然确定，这就要求库仑力卫星编队的惯性主轴必须与Hill模型的三个坐标轴重合。

在Hill坐标系中，任何一颗卫星的位置矢量可表示为

编队中第i个卫星相对FI系的速度可表示为

式中：为卫星在Hill模型中绕Z轴旋转的角速度；r为参考卫星的地心距。

每个卫星的动能可表示为

用拉格朗日方程建立动力学关系

式中：T为卫星的总动能；Qi＝Qig＋Qic［7］。此处：Qig，Qic分别为地球重力项和库仑力项，且

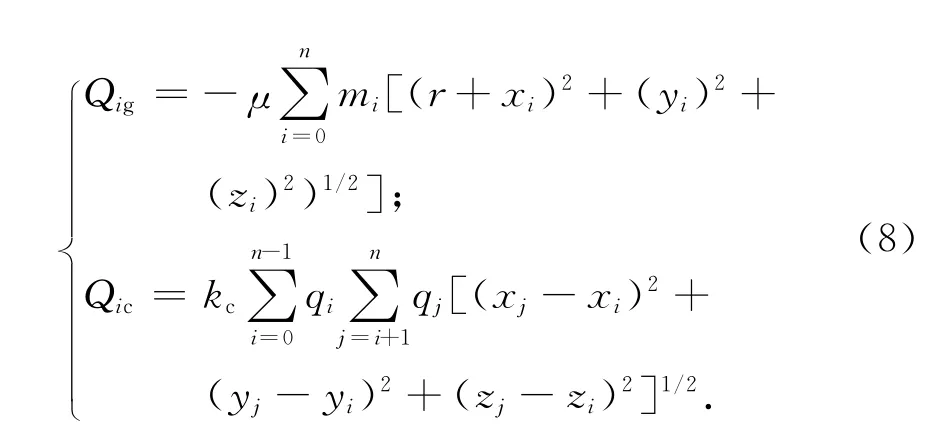
其中：μ为地球引力常量；kc为静电引力常量。将式（6）、（8）代入式（7）可得

将重力项整理成

在此基础上，用泰勒展开形式

因μ＝r3n2（n为卫星编队的平均轨道角速度），则可得

将式（12）代入式（9），并考虑德拜屏蔽效应，可得Hill模型中卫星库仑力编队的动力学方程

式中：ρij为两星间距，且ρij＝｜ρi－ρj｜。

4 编队基本平衡条件及两星状态简化

为使库仑力飞行编队中各星间的相对位置保持稳定，在不考虑扰动条件下，动力学方程式（13）中所有导数项均必须为零。具体编队构形是通过严格布置各卫星在编队中的位置和卫星的电势（电荷量）实现的。式（13）考虑了德拜屏蔽效应，在地球同步轨道上，含德拜长度的指数项可近似为1。

为使表达更简洁，将方程中的q，kc，n合称为一个参数，定义

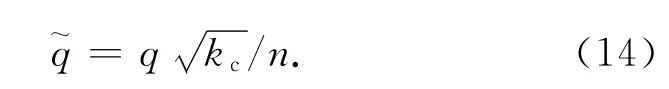
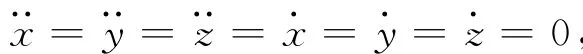
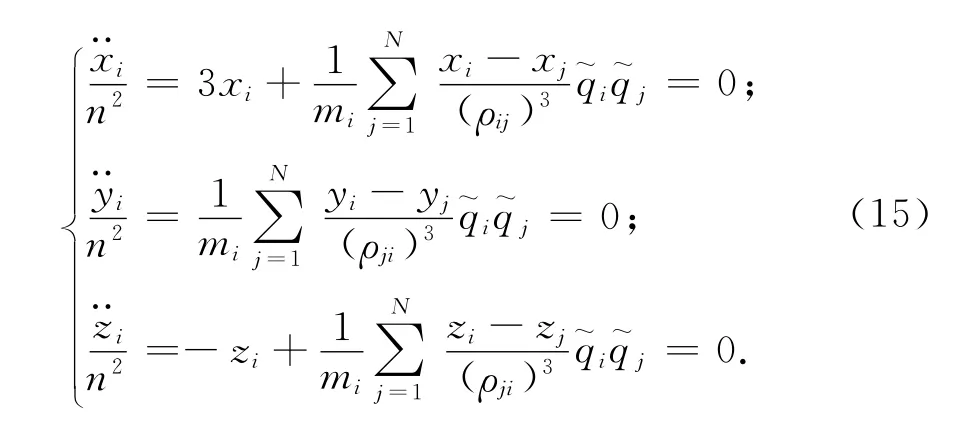
对一般N星问题，若卫星的编队按式（16）构形，则该库仑力卫星编队可达到稳定。

对两星问题，两星沿Hill坐标系X轴的编队如图2所示。两星的间距为L，两者的质心位于坐标原点，满足质心条件。因两者共线且位于X轴上，主轴条件自然满足。

图2X轴上两体编队Fig.2 Two-body formation flying inXaxis

根据质心条件可得

将两星的间距表示成第一颗卫星的坐标

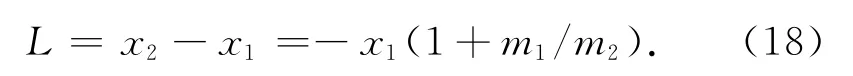
将此问题的编队形式代入Hill方程式，可得X向上的两组方程（每个卫星各有一个）

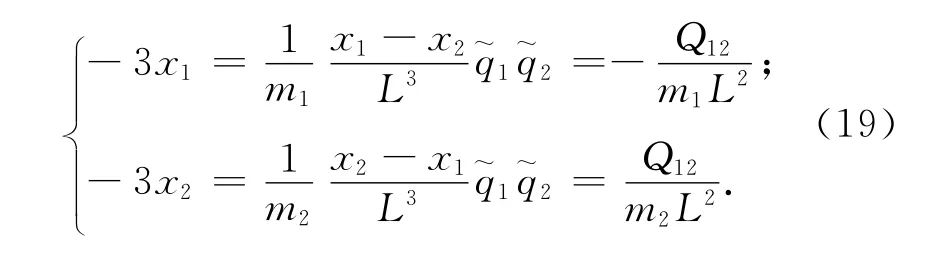
将式（17）、（18）代入式（19）中，解出Q12，编队构形方程为

同理，若设任意轴上的两星编队的构形方程为

则可得X、Z轴（即沿地心方向与沿轨道面法线方向）存在稳定构形，沿飞行方向则无稳定构形。任意轴上两星库伦力编队存在情况见表2。

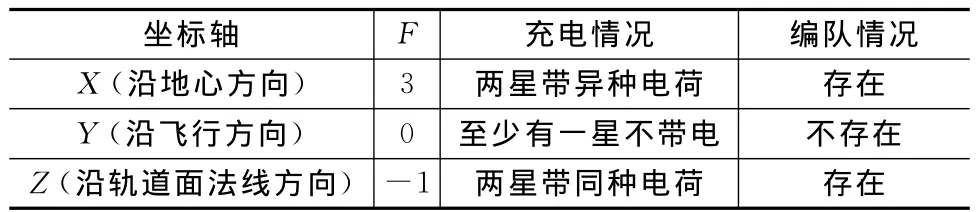
表2 任意轴上两星库伦力编队存在情况Tab.2 Pair coulomb satellite formation in random axis

5 数学仿真及结果分析

如前分析，理论上满足两星库仑力编队在Hill坐标系中任意轴上的稳定构形存在无穷多个，因此编队构形选择成为关键。本文针对X轴上的两星编队，讨论影响编队充点电势的因素，进而得到关于编队优化的一般性结论。为简化问题，假定编队内两卫星的质量（m1，m2为150kg）、体积和充电电势相等，r1＝r2＝2.5m，n＝＝7.291 5×10－5rad／s［12］。

根据格林公式和式（21），可得充电电荷

将式（22）代入式（20）可得卫星充点电势

数值仿真结果如图3所示。

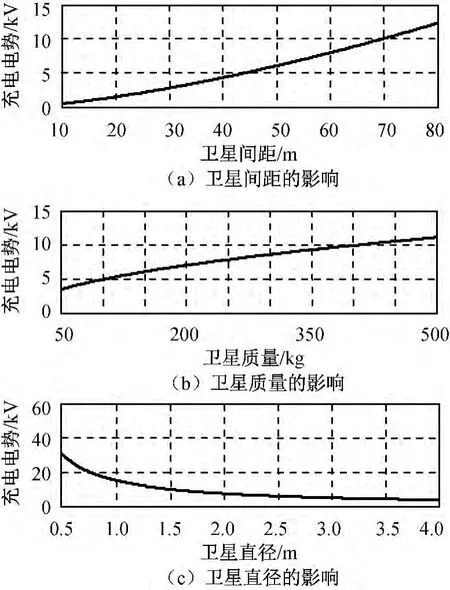
图3 库仑力编队电势Fig.3 Voltage for coulomb satellite formation

由仿真结果可知：对地球同步轨道库仑力编队，随着卫星间距的增大、卫星质量的增加，卫星所需充电电势逐渐增大；充电电势与卫星直径成反比关系，充电电势随卫星直径增大而快速下降。由此可知，为减小库仑力卫星编队所需电势以节约能源，应减小编队距离，减轻卫星重量，同时增大卫星外表面体积，提高库仑力编队的效率。

6 结束语

本文分析了库伦力编队空间德拜屏蔽效应，建立了基于拉格朗日方程的库仑力卫星编队动力学模型并得到简化模型，得到了编队系统达到稳定的基本平衡条件：基于地球同步轨道等离子环境中德拜长度在100～1 000m量级，相较近地和深空轨道，地球同步轨道为库伦力编队的最佳应用范围；双星地球同步轨道库伦力编队在沿地心方向与沿轨道面法线方向存在稳定构形；为提高库伦力编队效率节约能源，应减小编队距离，减轻卫星重量，同时尽可能增大卫星外表面体积。研究为后续N星库仑力编队的进一步分析提供了参考。

［1］ KRIEGHER G，MOREIRA A，FIEDLER H，et al.TanDEM-X：a satellite formation for high-resolution SAR interferometry［J］.IEEE Transactions on Geosciences and Remote Sensing，2007，45（11）：3317-3340.

［2］ PARKER G，SCHAUB H，NATARAJAN A，et al.Coulomb force virtual space structures［C］／／Workshop on Innovative Systems Concepts，Noordwjik：［s.n.］，2006：39-44.

［3］ GARRETT H B，SCHWANK D C，DEFROST S E.A statistical analysis of the low energy geosynchronous plasma environment［J］. Protons Planetary Space Science，1981，29（10）：1021-1044.

［4］ MULLEN E G，GUSSENHOVEN M S，HARDY D A.SCATHA survey of high-voltage spacecraft charging in sunlight［J］.Journal of Geophysical Research，1986，91（7）：74-90.

［5］ CHONG J H.Dynamic behavior of spacecraft formation flying using coulomb forces［D］. Houghton：Michigan Technological University，2002.

［6］ NATARAJAN A.A study of dynamics and stability of two-craft coulomb tether formations［D］.Blacksburg：Virginia Tech，2007.

［7］ SCHAUB H，PARKER G G，KING L B.Simulated Reprint from Journal of the Astronautical Sciences.2004，45（3）：169-193.

［8］ PETTAZZI L，KRUGER H，THEIL S.Electrostatic force for swarm navigation and reconfiguration［J］.Acta Futura，2008，26（4）：80-86.

［9］ NICHOLSON D R.Introduction to plasma theory［M］.Malabar：Krieger Pub Co，1992：56-89.

［10］ PARKER G，KING L B，SCHAUB H.Steered spacecraft deployment using interspacecraft coulomb forces［C］／／American Control Conference.Minneapolis：［s.n.］，2006：14-36.

［11］ SCHAUB H.Stabilization of satellite motion relative to a coulomb spacecraft formation［J］.Journal of Guidance，Control and Dynamics，2005，28（6）：1231-1239.

［12］ BERRYMAN J，SCHAUB H.Analytical charge analysis for two-and three-craft coulomb formations［J］.Journal of Guidance，Control，and Dynamics，2007，30（6）：1701-1710.