磁悬浮力矩陀螺内外框架低速高精度控制技术研究

李延宝，李结冻，孙宏丽，于常利，卢 山

（1.上海航天控制技术研究所，上海 201109；2.上海市空间智能控制技术重点实验室，上海 201109）

0 引言

随着航天技术的发展，动量交换装置因其输出范围大、响应快且可连续变化、不消耗工质等优点而更多地用于航天器姿态控制系统［1］。磁悬浮控制力矩陀螺（MSCMG）是空间站等大型航天器实现姿态控制的关键执行机构，其精度直接决定了航天器的姿态控制精度，而MSCMG的框架系统是影响其输出力矩精度的重要因素［2］。DGMSCMG不仅满足高精度、长寿命要求，而且可减小姿控执行机构的体积和质量，是航天器实现高精度和快速机动姿控的理想执行机构［3］。控制力矩陀螺的高精度伺服系统用于解决各种干扰对框架系统的可靠工作产生的破坏，克服了摩擦力矩、不平衡力矩等外部扰动力矩，与内部高速磁悬浮转子的耦合力矩，框架转动惯量变化带来的系统大范围参数变化等不确定性［4］。文献［5］采用一种前馈方法，不但对时间滞后进行补偿，而且只需很小的调节系数就能满足系统带宽要求，提高了系统的稳定裕度。为提高磁悬浮转子系统的稳定性，文献［6］提出了一种基于复合控制的补偿方法，通过磁轴承产生相应的电磁力，对陀螺耦合力矩和惯性耦合力矩进行补偿控制。文献［7］提出用角加速度反馈的方式增加系统的主动阻尼，降低谐振的影响。该法利用加速度传感器检测负载端的加速度，而陀螺框架在负载端只有角位置传感器，故加速度信息估计较难。文献［8-9］将数字滤波器用于控制系统以抑制振动，其应用范围是谐振频率点100Hz以上，用实验验证陀螺框架系统的谐振频率点约30Hz。文献［10］提出将输出轴扭矩的微分反馈至电机控制端，但该法中扭矩的估计对噪声非常敏感，很难正确估计扭矩。文献［11］在系统参数存在非线性变化条件，利用ESO观测谐波减速器输入及输出端的扰动，通过反馈及前馈对扰动进行振动抑制。

本文针对磁悬浮力矩陀螺内外框架低速高精度控制技术问题，建立了航天器内外框架动力学模型，基于它们间的非线性耦合未知干扰，利用基于扩张状态观测器的扰动力矩估计器获取补偿力矩，在常规的PID控制器中通过前馈方式对内外框架进行前馈力矩补偿。并进行了数学仿真试验。

1 坐标系及变量定义

惯性坐标系oi－xiyizi：原点oi位于地心；oixi、oiyi轴分别指向春分点和北极，并与oiyi轴构成右手坐标系。

航天器本体坐标系ob－xbybzb：原点ob为航天器质心；obxb、obyb、obzb轴固定在卫星体上，且为卫星的三个惯量主轴。

DGMSCMG安装参考坐标系os－xsyszs（外框架坐标系在零位置时与之重合）：与本体系固联。为第i个DGMSCMG的参考坐标系至本体系的转换矩阵，并与各DGMSCMG在航天器上的安装方位有关，且为常值矩阵。

外框架坐标系o-x1y1z1、内框架坐标系o-x2y2z2：两者原点与陀螺仪的支承中心重合。当陀螺绕外框架轴正向以角速度相对参考坐标系转动α时，并绕内框架轴以角速度相对参考坐标系转动β，坐标系间的位置关系如图1所示。

2 内、外框架伺服系统耦合动力学建模与分析

2.1 高速转子的转动惯量

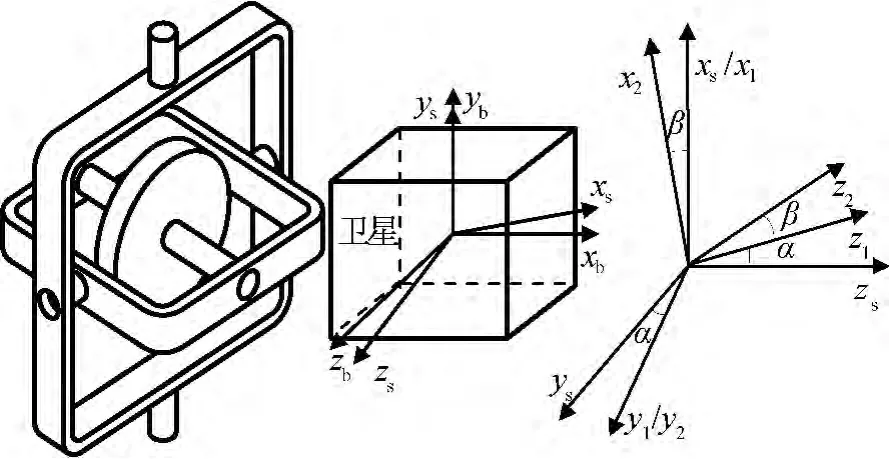
图1 框架坐标系Fig.1 Frame coordinate system of DGCMG

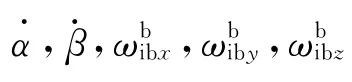
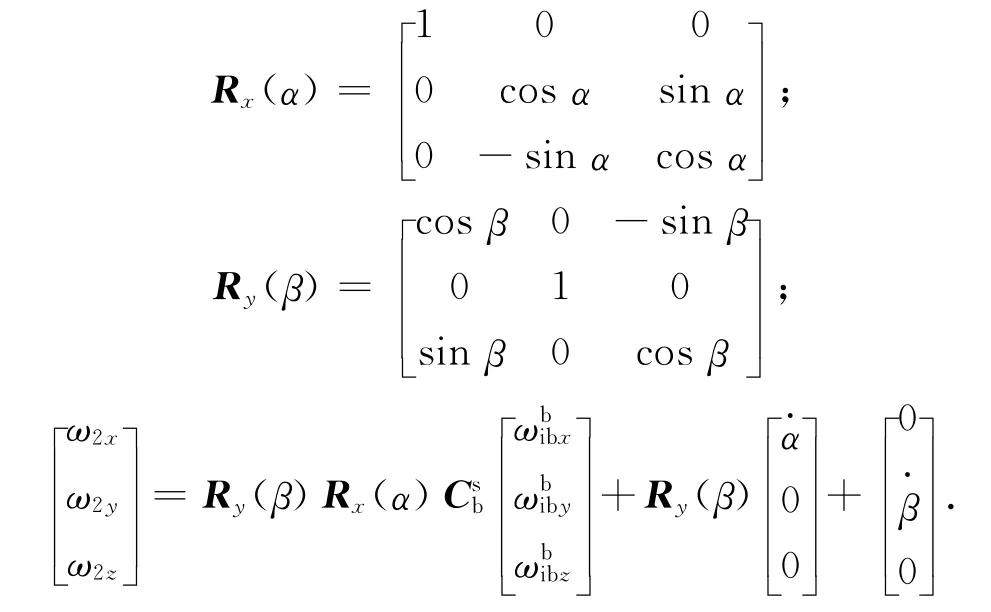
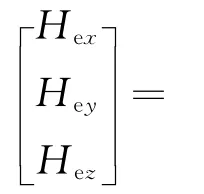
2.2 内框架组件绕内框架轴转动动力学方程

令内框架相对o-x2y2z2系在各轴的转动惯量为J2x，J2y，J2z，则内框架动量矩在o－x2y2z2系的投影为H2x，H2y，H2z（即J2xω2x，J2yω2y，J2zω2z）；内框架组件（内框架和转子）动量矩在o-x2y2z2系的投影为H′2x，H′2y，H′2z（即H2x＋Hex，H2y＋Hey，H2z＋Hez）。

由欧拉动力学方程可得

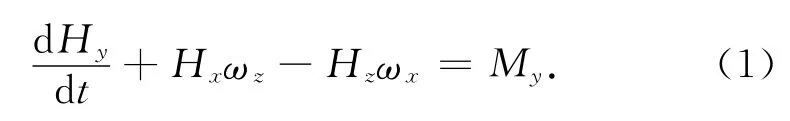
式中：Hx，Hy，Hz分别为转子在x、y、z向的角动量；ωx，ωz为转子相对oi－xiyizi系角速度；My为磁轴承在y向的主动控制力矩。则可得内框架组件的动力学方程

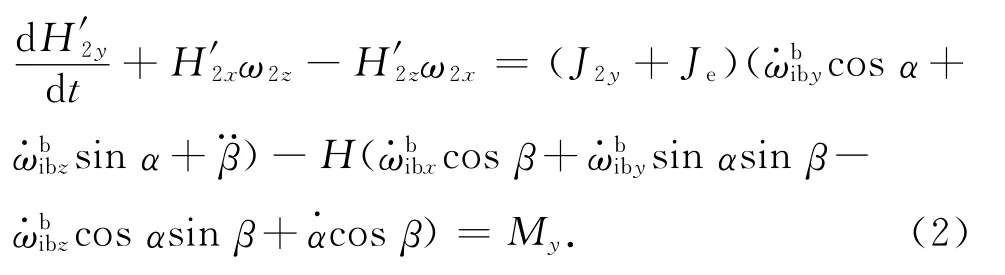
2.3 外框架组件绕外框架轴转动动力学方程

令外框架相对o-x1y1z1系的转动惯量分别为J1x，J1y，J1z，则 外框架相 对ob－xbybzb系 的 角 速度为

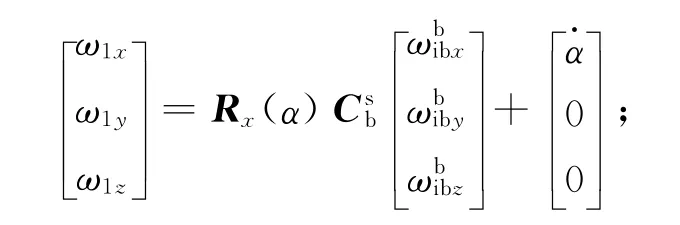
内框架组件动量矩在o-x1y1z1系的投影为

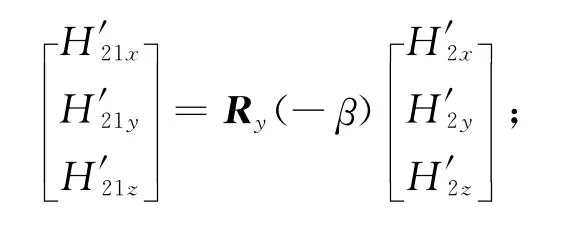
外框架动量矩在o-x1y1z1系的投影为

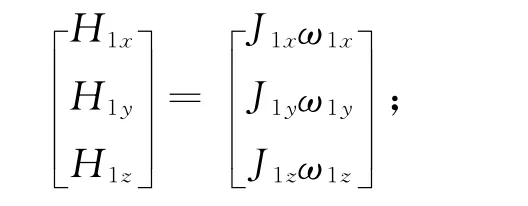
外框架组件动量矩在o-x1y1z1系的投影为

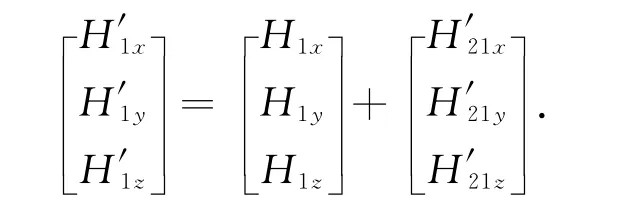
由欧拉动力学方程可得

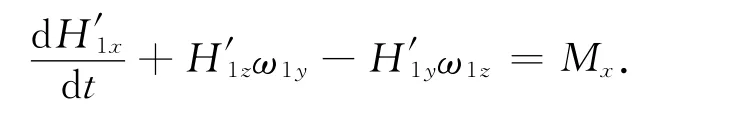
则可得外框架组件的动力学方程

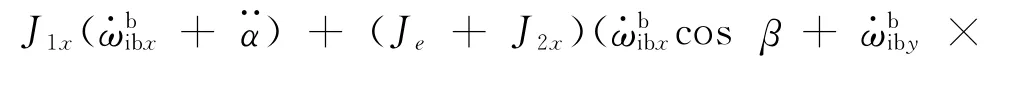
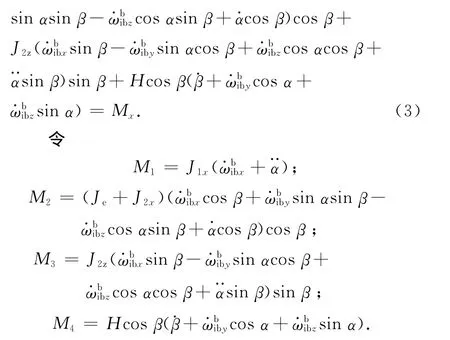
物理意义为：M1为外框架轴上的惯性力矩；M2为内框架组件在o-x2y2z2系ox2轴上的惯性力矩最终在外框架ox1轴上的投影；M3为内框架组件在oz2轴上的惯性力矩最终在外框架ox1轴上的投影；M1，M2，M3之和为惯性力矩；M4为航天器运动引起的陀螺力矩，其中Hβ·cosβ为内框架运动引起的陀螺力矩。

3 框架轴系低速高精度控制

对受未知扰动影响的非线性不确定系统，其数学表达式可表示为x（n）＝f（x，x（1），x（2），…，x（n－1），t）＋w（t）＋bu（t）。此 处：中f（x，x（1），x（2），…，x（n－1），t）为未知函数；w（t）为未知扰动；u（t）为控制输入量；x，x（1），x（2），…，x（n－1）为系统的状态变量，x（t）可测或间接可测。令x1＝x（t），x2＝x′（t），xn＝xn－1（t），则系统可表示为

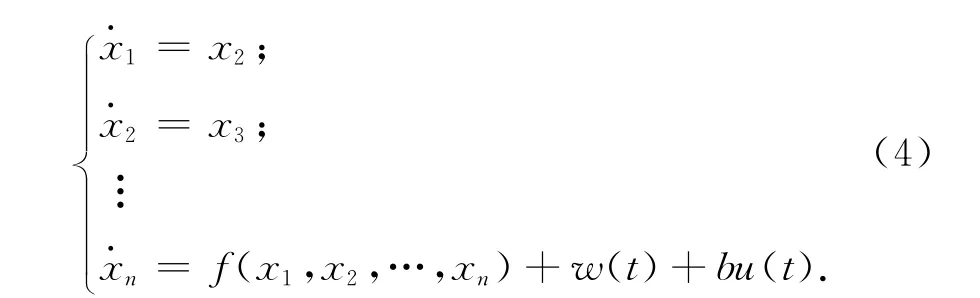
构造非线性系统

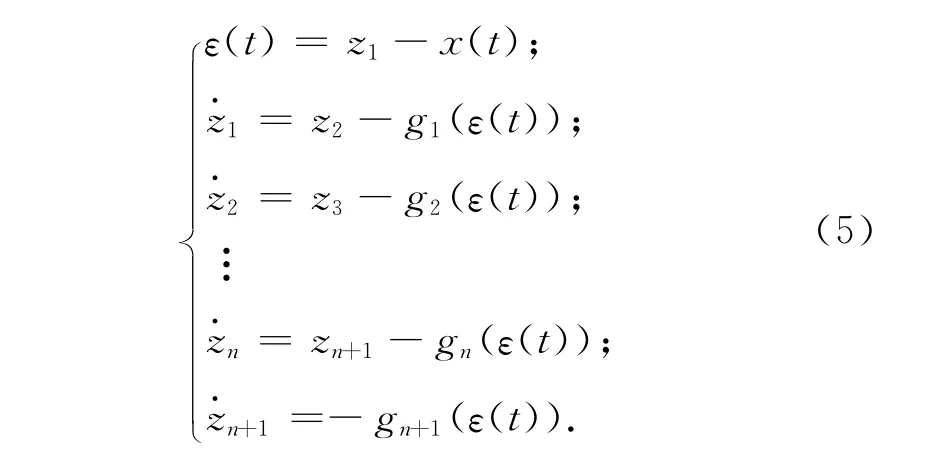
令a（t）＝f（x（t），t）＋w（t），若选择的非线性函数g（z）合适，则能使式（5）系统中的各变量正确跟踪式（4）中的各变量，zn＋1正确跟踪综合扰动a（t），在控制系统中加入相应的补偿，使系统具较强的适应能力。令gi（z）＝kig（z），i＝1，2，…，n－1，此处g（z）为非线性函数，则式（5）可表示为

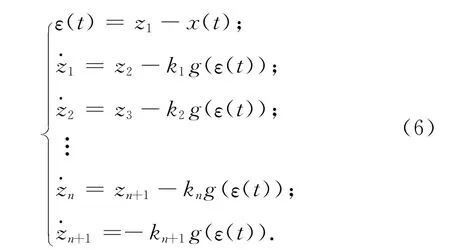
其中g（z）的选取规则为：g（z）连续可微；g（0）＝0；g′（z）≠0。因此选定非线性函数g（z）＝（1－ez）／（1＋ez），以下考虑k1，k2，…，kn＋1的设计。

在基于单轴气浮台的DGMSCMG集成实验中ωibz＝，相应的内、外框架的动力学方程分别为

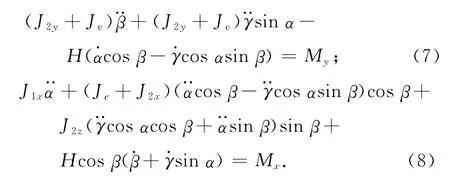
由式（7）、（8）可知：在 DGMSCMG的框架伺服系统中，存在内外框架间的耦合力矩及航天器运动耦合到内外框架上的牵连力矩。上述扰动力矩给框架伺服系统的高性能控制带来了极大的困难。

利用基于扩张状态观测器的扰动力矩估计器获取补偿力矩，在常规的PID控制器中通过前馈方式进行力矩补偿，以内框架为例介绍干扰力矩观测器的设计。将内框架动力学方程改写成 （J2y＋Je＋Md＝My，此处Md为扰动力矩，负载端的状态方程可写为

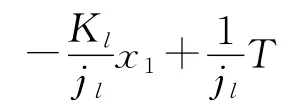
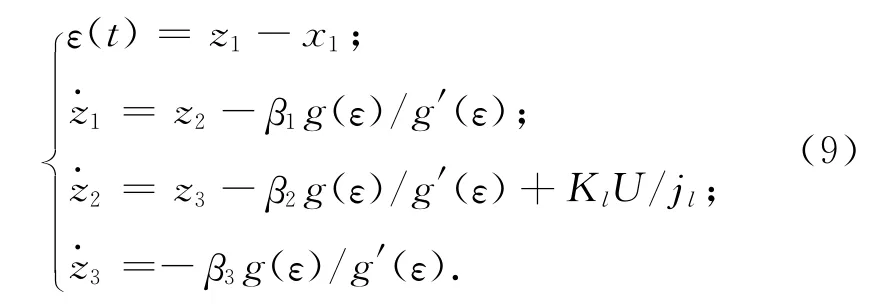
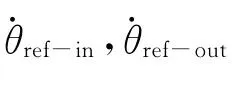
4 仿真分析

为验证基于扩张状态观测器的扰动力矩估计器，以内框架为例，分别对系统中存在干扰力矩但未加干扰力矩补偿，以及系统中存在干扰力矩并加干扰力矩补偿的角速度进行仿真。取系统模型仿真参数为转子质量4.5m／kg；转子径向转动惯量Je＝0.011 9kg·m2；转 子 轴 向 转 动 惯 量Jz＝0.022 9kg·m2；磁轴承电流刚度ki＝220N／A；磁轴承位移刚度kh＝0.7MN／m；内框x向转动惯量J1＝0.020 8kg·m2；外框y向转动惯量J2＝0.039 6kg·m2。

未加力矩补偿时，框架伺服系统的角速度调节曲线如图3所示。由图可知：干扰力矩严重影响框架伺服系统的速度调节性能。加入基于ESO的干扰力矩估计器并通过前馈的方式对力矩进行补偿后，仿真结果如图4所示。由图可知：在同样的控制参数下加入的扰动力矩补偿明显改善了框架伺服系统的速度调节性能，不仅使速度调节有好的快速性，而且提高了系统的稳态精度。

内框架牵连力矩的估计结果如图5所示（由两段时间图6、7组合而成）。由图可知：该时间段在外框架出现阶跃时，耦合到内框的牵连力矩，由图6、7可发现，基于扩张状态观测器的力矩估计可较好地跟踪实际力矩的变化，仅滞后0.005s，对框架10Hz的控制带宽，完全满足要求。

上述仿真表明：ESO的扰动力矩估计器对扰动力矩的估计能实时跟踪扰动力矩。采用前馈力矩补偿后可缓和耦合力矩和牵连力矩的阶跃影响，使输出力矩平滑，提高控制精度。

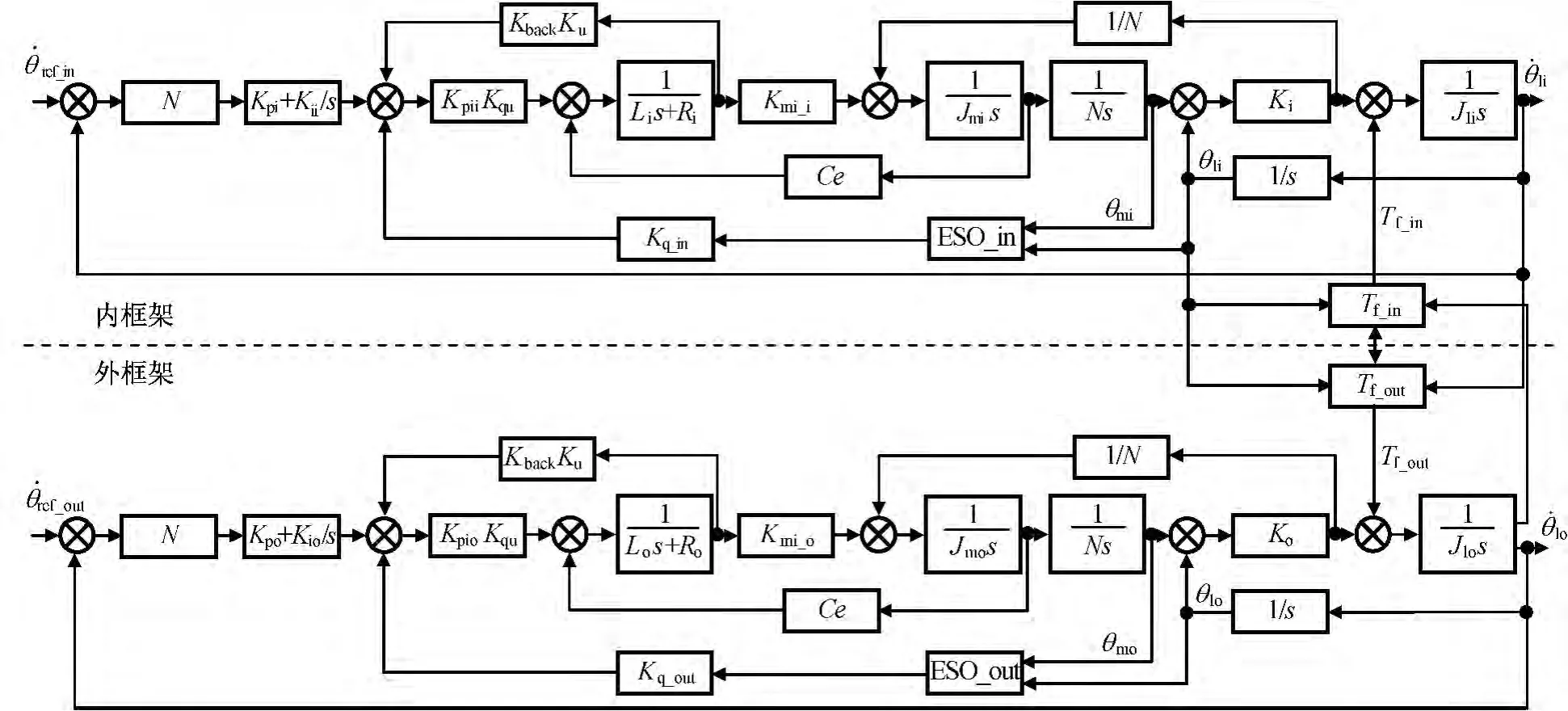
图2 低速高精度控制结构Fig.2 Control structure of low speed and high precision system

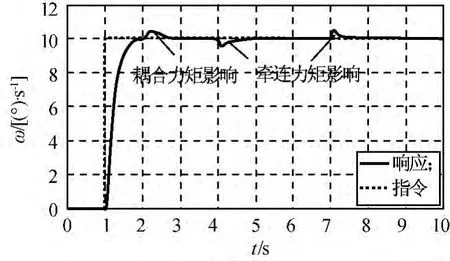
图3 力矩补偿前内框架阶跃响应Fig.3 Inner-gimbal step response without moment compensation

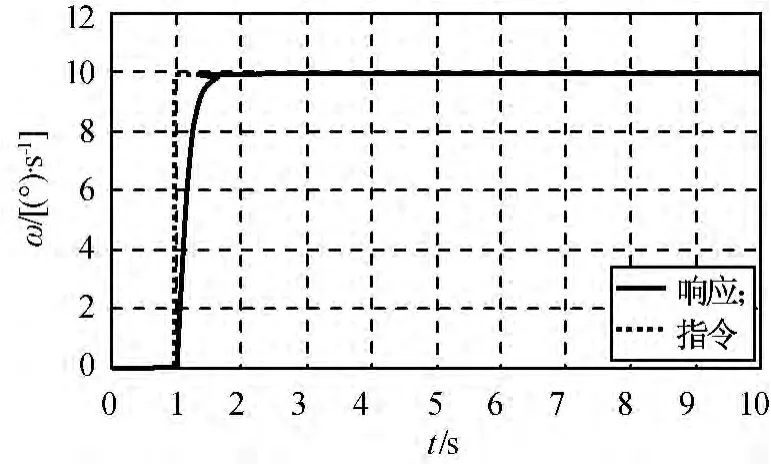
图4 力矩补偿后内框架阶跃响应Fig.4 Inner-gimbal step response with moment compensation

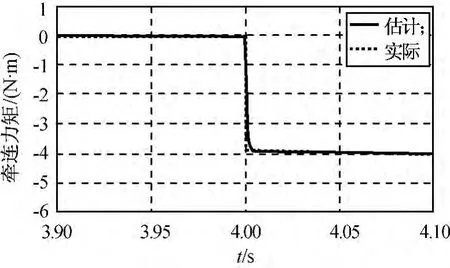
图6 内框架牵连力矩估计1Fig.6 Inner-gimbal moment estimation 1

5 结束语

本文建立了基于磁悬浮双框架控制力矩陀螺内外框架转动动力学模型，基于其间的非线性耦合未知干扰，用基于扩张状态观测器的扰动力矩估计器获取补偿力矩，在常规的PID控制器中通过前馈方式对内外框架进行前馈力矩补偿。仿真结果表明：干扰力矩严重影响了框架伺服系统的速度调节性能；加入基于ESO的干扰力矩估计器并通过前馈的方式对力矩进行补偿后，在相同的控制参数下加入的扰动力矩补偿使框架伺服系统的速度调节性能显著改善。不仅使速度调节具有较高的快速性，而且提高了系统的稳态精度。

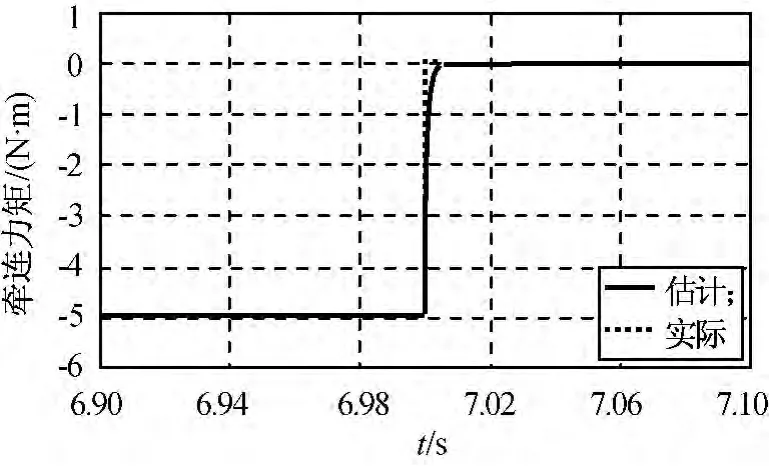
图7 内框架牵连力矩估计2Fig.7 Inner-gimbal moment estimation 2

［1］ 王 磊，赵育善，李 云.平行构型双框架控制力矩陀螺操纵律研究［J］.宇航学报，2009，30（4）：1551-1563.

［2］ 徐向波，房建成.基于角加速度的陀螺框架伺服系统干扰观测器［J］.北京航空航天大学学报，2009，35（6）：669-672.

［3］ 杨 倩，崔培玲，韩邦成，等.航天器机动时DGMSCMG磁悬浮转子干扰补偿控制［J］.宇航学报，2012，33（6）：720-727.

［4］ 于灵慧，房建成.磁悬浮控制力矩陀螺框架伺服系统扰动力矩分析与抑制［J］.宇航学报，2007，28（2）：287-291.

［5］ 李建文，刘 刚，李 红.磁悬浮控制力矩陀螺框架伺服系统前馈补偿模糊控制方法［J］.微电机，2009，42（5）：35-42.

［6］ 杨 倩，崔培玲，韩 邦，等.航天器机动时DGMSCMG磁悬浮转子干扰补偿控制［J］.宇航学报，2012，33（6）：720-727.

［7］ FUTAMI S，KYURA N，HARA S.Vibration absorption control of industrial robots by acceleration feedback［J］.IEEE Transactions on Industrial Electronics，1983，IE-30（3）：299-305.

［8］ VUKOSOVIC S N，STOJIC M R.Suppression of torsional oscillations in a high performance speed servo drive［J］.IEEE Transactions on Industrial Electronics，1998，45（1）：108-117.

［9］ ELLIS G，LORENZ R D.Resonant load control methods for industrial servo drives［C］∥ Proceedings of the IEEE Industry Application Society Annual Meeting.［s.l.］：IEEE，2000，3（2）：1438-1445.

［10］ SUGIURA K.HORI Y.Vibration suppression in 2and 3mass system based on the feedback of imperfect derivative of the estimated torsional torque［J］.IEEE Transactions on Industrial Electronics，1996，43（1）：56-64.

［11］ 李海涛，房建成.基于扩张状态观测器的DGMSCMG框架伺服系统振动抑制方法［J］.航空学报，2010，31（6）：1213-1219.