一种基于时频分解的多目标速度估计方法

谭姗姗，王志诚，余渝生，刘庆波

（上海无线电设备研究所，上海 200090）

0 引言

频率步进信号是一种利用瞬时窄带信号合成宽带信号，在获得距离高分辨性能的同时降低了对接收机带宽和采样率的要求，易于工程实现。因存在距离－多普勒耦合，是一种多普勒敏感信号，目标径向运动会造成距离走动和波形发散，故必须进行速度补偿。传统补偿方法是对回波信号乘以相应的补偿因子，但当多个目标在距离维无法分辨时，方法会失效，不能实现运动补偿［1－2］。文献［3］用修正的多项相位变换方法对线性调频连续波（LFMCW）雷达多目标加速度和速度进行估计，但存在较严重的误差积累效应，且对高阶加速度的求取需要更高的信噪比，故其鲁棒性尚需进一步完善。文献［4］用频域补偿方法实现多目标存在相对运动时的补偿，但当多个不同速度的目标处于同一距离分辨单元时则难以分辨。针对多个不同速度的目标在距离单元不能分辨的情况，本文研究了一种基于时频分解的多目标速度估计算法。

1 多目标回波信号分离和重构

1.1 S-method分布算法

短时傅里叶变换是经典的时频分析算法，其计算可由窗函数沿信号滑动实现。信号x（n）离散时间形式的短时傅里叶变换定义为

式中：n为时间序号；k为频率序号；N＋1为信号x（n）的长度；w（m）为窗函数；j为虚数单位。w（m）的有效宽度越窄（有效时长越短），其分析信号局部频谱特性的能力就越强，反之则越差。

信号x（n）的S-Method分布定义为

式中：L为计算S-Method分布的计算项数［5］。为更好地利用信号的能量，计算信号的S-Method分布时，选取的L值应大于信号带宽对应的数值。当多个目标在频域上的间距小于目标的带宽时，若按此原则选取L，会导致L大于目标速度间距，出现交叉项，导致两个目标无法分辨。若L选取过小，虽可将信号分离开，但不能充分利用信号的能量，导致信号能量不足，特征值过小，造成信号漏检等问题。因此，应根据实际和需求选择合适的L值，具体可参考文献［6］。

S-method分布满足多分量信号的线性可加性，同时通过选取适当的L值可获得较好的频率分辨力，且信号的能量聚集度高。这是S-Method分布相对其他经典时频分布的优势。

1.2 多目标信号分离和重构

对一个包含p个不同速度的目标的回波信号

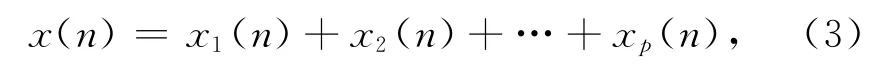
为对x（n）中每个不同速度的目标的回波信号进行分离和重构，按以下步骤进行。此处：n＝1，2，…，N－1，N。

a）由式（2）计算x（n）的S-method时频分布，构造相关矩阵

式中：n1，n2为时间序列，且n1，n2＝1，2，…，N。

b）对R作特征分解

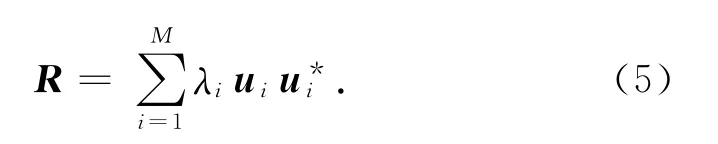
式中：λi为特征值；ui为λi对应的特征向量；为ui的共轭向量。

c）选取R的前p个最大特征值λi，1＜i＜p，并用其对应的ui重构目标信号

式中：xi＝［xi（1）xi（2） …xi（N）］＝xi（n）。xi即为所重构的p个目标的回波信号。

2 多目标速度估计方法

2.1 利用相邻帧相位差的单目标速度估计算法

设频率步进信号的起始载频为f0，频率步进阶梯为ΔF，频率步进脉冲数积累为N1，脉冲重复周期为Tr，脉冲宽度为τ。对一个初始径向距离为R、速度为v的匀速运动目标，其回波经由相参接收机后的输出

式中：c为光速；t为雷达对目标的观测时间。

以一组N个脉冲为1帧，相邻两帧回波数据分别记为第1帧S1和第2帧S2，分别取S1，S2中对应的第m个距离单元的N个采样值，记为s1m，s2m。设第一帧对应的时刻t＝t1，则由式（7），s1m可表示为

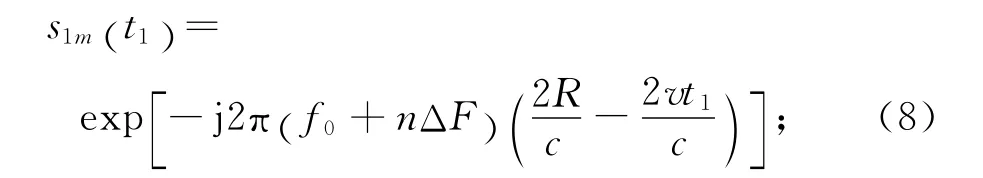
第二帧对应的时刻t＝t2，则s2m可表示为

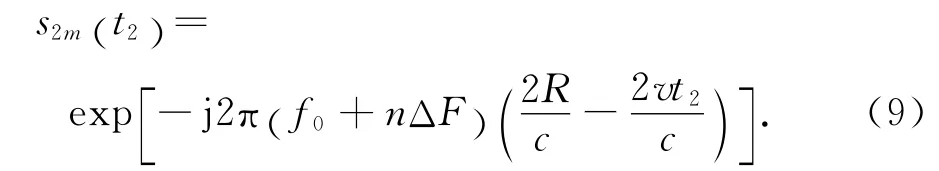
由式（7）、（8）可得相邻两帧同一距离单元的数据s1m，s2m间的相位差

由图1可知：t2－t1＝NTr，则

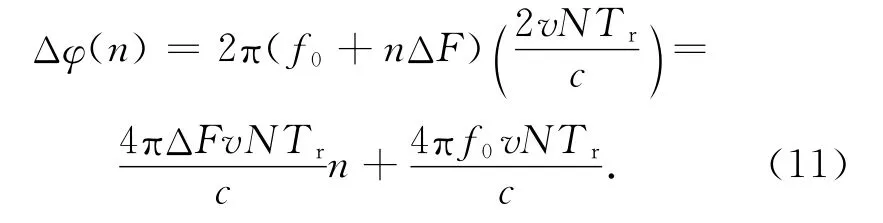
图1中：ΔR＝2vNTr。由式（10）可知：Δφ为由目标在一帧时间NTr内所运动的距离ΔR产生的相位差。

图1 目标相邻帧回波数据间的时间与距离的关系Fig.1 Relationship of time and distance of adjacent frames of target echo

若将式（11）中的速度v作为一个已知常数，积累脉冲数n为自变量，则式中的Δφ（n）是一个关于变量n的线性函数，Δφ（n）满足直线的斜截式方程

式（11）中第一项4πΔFvNTrn／c是与n成正比的比例项，其斜率k＝－4πΔFvNTrn／c；第二项4πf0vNTr／c是常量，可视为直线的截距b。只要求解Δφ（n）的斜率k，便可反推得到

实际应用中，Δφ（n）并不是理想的直线。一方面，由于Δφ的取值范围为［－π，π］，当目标的速度较大时，Δφ会在n＝1，2，…，N间出现多次折叠；另一方面，由于噪声的影响，Δφ会叠加噪声相位，产生相位抖动。由于上述因素的存在，难以直接由Δφ求解出其斜率k。对此，本文先对折叠的相位进行相位解卷绕，使Δφ由折线变成直线，再用直线拟合的方式对整条直线进行拟合，求解其斜率k［7－8］。相位解卷绕和直线拟合算法参见文献［7-8］。

综上，对单目标回波，基于相邻帧相位差的速度估计算法的流程如图2所示。

2.2 多目标速度估计算法流程

对有p个目标的频率步进回波信号进行速度估计步骤如下。

a）先用S-method时频分解方法对回波进行预处理，分离多目标回波信号，多目标速度估计问题转为单目标速度估计问题。

b）用本文的相邻帧相位差的速度估计方法对分离的单个目标逐一进行速度估计。

信号处理流程如图3所示。

3 仿真计算

图2 用信号相邻帧相位差的单目标速度估计算法流程Fig.2 Process for single target velocity estimating by phase differential of adjacent frame algorithm

图3 基于时频特征分解的多目标速度估计算法流程Fig.3 Process for multi-target velocity estimating based on time-frequency eigen decomposition

设f0＝10GHz，Tr＝20μs，τ＝2μs，ΔF＝0.5MHz，N1＝256，fs＝10MHz。回波中包含两个目标：目标1、2处于同一个距离分辨单元内，速度分别为v1＝250m／s，v2＝500m／s，时域信噪比－3dB，进行仿真计算。

相邻两帧的回波数据如图4所示。搜索寻找目标所在的距离单元的数据，取第一、二帧回波数据目标所在距离单元的数据，分别记为S1，S2，作为待分析数据，其数据长度与相同。

用S-method算法对S1，S2进行时频分析，所得结果XSM1，XSM2如图5所示。

XSM1，XSM2通过构造R阵并进行特征值分解后的特征值，结果如图6所示。由图6可知：前两个特征值较大，其开根号值分别对应目标1、2的重构信号幅值。由式（5），用这两个较大的特征值及对应的特征向量可分别重构出两个目标的信号如图7所示。

求出图7（a）、（b）中目标1重构信号的相位差，如图8（a）所示，图7（a）、（b）中目标2重构信号的相位差，如图8（b）所示。用相位解卷绕和直线拟合算法分别对图8中的数据进行拟合，结果如图9所示。其中：目标1、2的相位差的拟合直线斜率分别为0.026 2，0.055 5，用式（13）估计出的目标1、2的速度分别为244.8，517.9m／s。

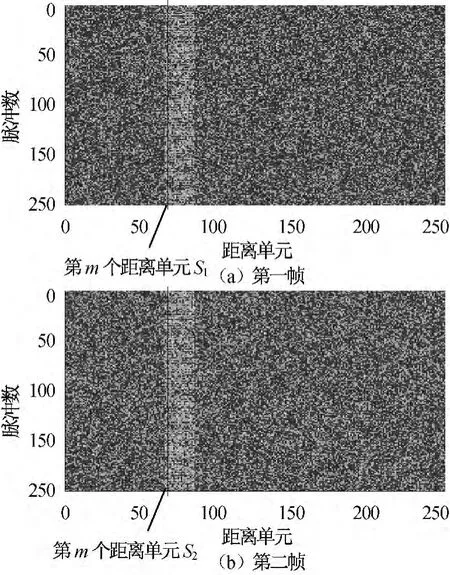
图4 频率步进信号相邻两帧回波数据Fig.4 Adjacent frame echo of stepped frequency signal

4 性能分析

4.1 多目标分辨能力

本文的多目标速度估计方法对多目标的分辨能力取决于S-method时频分解对多目标的分辨力。若目标速度的差值大于一定的范围时，通过选取合适的L值，使两个目标在S-method分布的时频域上的相互影响尽量小，使重构信号的相位最大限度地保持线性特性，从而保证在对重构信号进行速度估计的精度。仿真试验表明，当两个目标的速度差值大于50m／s时，本文的多目标速度估计方法能有效进行速度估计。

图5 目标所在距离单元数据S-method时频分析结果Fig.5 S-method time-frequency analysis results of targets range cell

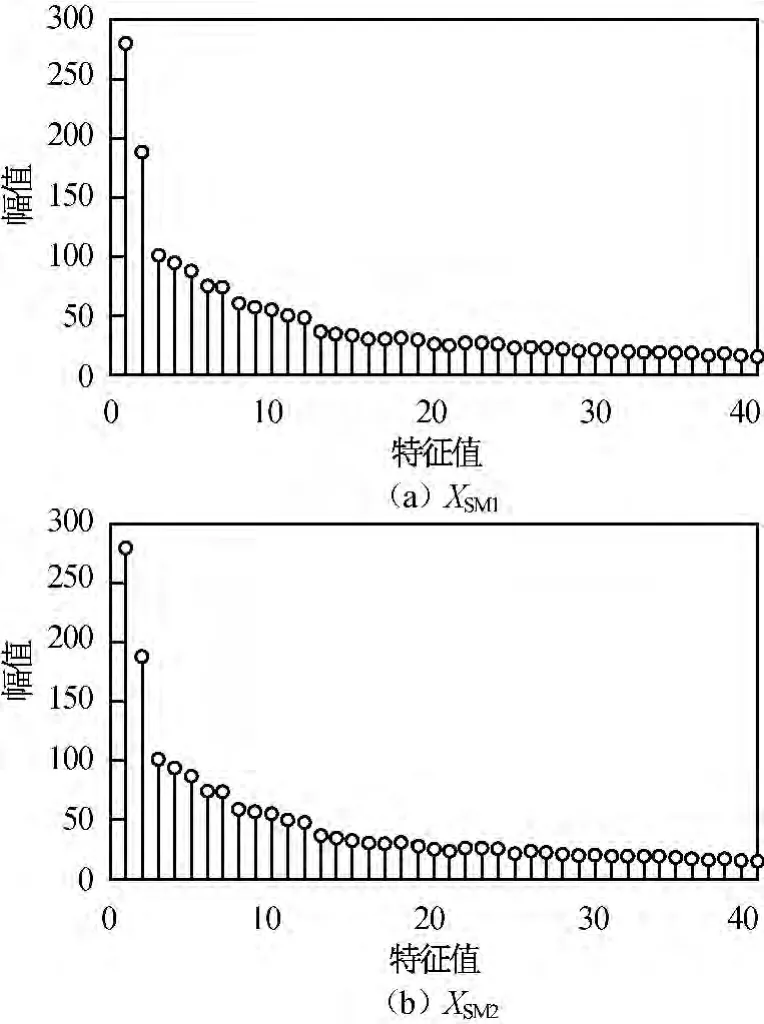
图6 时频分解后的特征值Fig.6 Eigen values of time-frequency decomposition

图7 分离并重构目标1、2的信号Fig.7 Reconstruct signals of two targets

图8 目标1、2的相邻帧信号的相位差Fig.8 Phase differential of adjacent frame of two targets

4.2 S-method时频特征分解对测速性能的影响

因S-method时频分解所重构的信号与实际单个目标的回波信号间存在差异，并不能完全无失真地恢复单目标信号，因此用所重构的单目标信号进行速度估计的误差也大于直接对单目标回波信号进行速度估计，且存在一个固定的差值，该固定差值源于重构信号失真。在信噪比足够的条件下，包含两个目标的多目标回波信号进行速度估计的蒙特卡洛试验的结果如图10所示，目标1的运动速度250m／s，蒙特卡洛试验的速度估计均值236.5m／s，速度估计均方差1.36m／s；目标2的运动速度350m／s，蒙特卡洛试验的速度估计均值332.6m／s，速度估计均方差3.5m／s。

信噪比相同时，若雷达接收回波中只有一个速度250m／s的单目标，无需用S-method时频分解进行目标分离预处理，可直接用相邻帧相位差单目标速度估计方法对目标进行速度估计，蒙特卡洛试验500次，结果如图11所示，单目标速度估计均值250m／s，速度估计均方差1.63m／s。

根据以上分析，基于时频分解的多目标速度估计方法适于对频率步进信号体制雷达的多目标回波进行较粗略的速度估计。

5 结束语

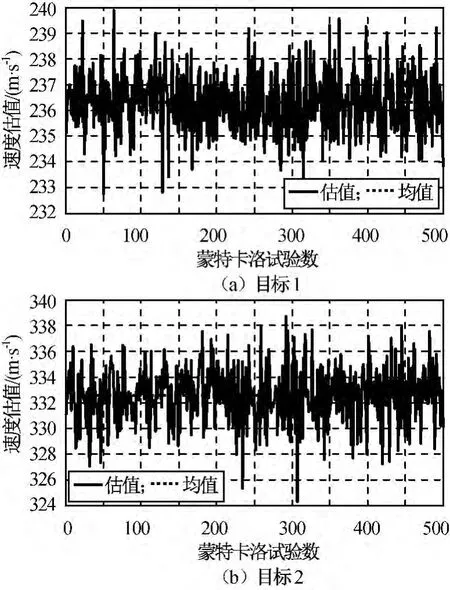
图10 多目标回波的速度估计值Fig.10 Estimated value of velocity for multi-targets echo

针对频率步进信号体制雷达中的同一距离分辨单元存在多目标时的速度估计和补偿的问题，本文提出了一种可行的解决方案。用S-method时频分解法将多目标回波中的每个目标进行分离和重构，用重构信号对每个目标分别进行速度估计，可进行速度补偿等后续信号处理，解决了多目标速度估计的问题。利用频率步进信号的相邻帧相位信息进行速度估计的方法具有测速范围大的优点，适于对多个匀速运动目标进行粗略速度估计。

图11 单目标回波速度估值Fig.11 Estimated value of single target echo

［1］ TAN K K，YU J，YUAN X Z.Existence theorems of nashequlibria for non-cooperativen-person games［J］.Game Theory，1995，24：217-222.

［2］ YU J.Essentiai equilibria of n-person noncooperative games［J］. Toumal of Mathematical Econmicsl，1999，31：361-372.

［3］ 张容权，李 政，杨建宇.LFMCW雷达多目标加速度和速度估计方法［J］.电讯技术，2005（6）：17-20.

［4］ 郭 昕，曾 涛，刘 鹤.频率步进雷达多目标频域运动补偿［J］.北京理工大学学报，2009，29（9）：830-832.

［5］ STANKOVIC L J.A method for time-frequency analysis［J］.IEEE Trans Signal Process，1994，42（1）：225-229.

［6］ 于 洋.基于S-Method特征分解的高频雷达机动目标信号处理［D］.哈尔滨：哈尔滨工业大学，2009

［7］ 任 毅，袁 晓.数字信号处理中相位解卷绕问题分析［J］.电脑开发与应用，2007，20（10）：42-43.

［8］ 许海涛，高彩霞.直线拟合算法［J］.电脑知识与技术，2009，5（4）：864-867.