轴对称双阱势的简化模型及其能级

屈 奎，倪致祥

(阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037)

轴对称双阱势的简化模型及其能级

屈 奎，倪致祥

(阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037)

给出了一般轴对称双阱势的一个简化模型，对薛定谔方程进行了严格求解，得到了波函数与能级方程，并利用Mathematica进行了数值计算，讨论了势垒的平均高度对能量本征值的影响, 发现随着平均势垒高度的增加，能级的值也在不断增加，最后趋向于一个确定的极限值。

轴对称；双势阱；狄拉克势垒；能级

双阱势问题在物理学中具有重要的理论意义和应用价值[1-10],比如组成双原子分子的两个原子核在成键时的库仑势就可以看成双阱势。然而，除了极个别的案例，在一般情况下双阱势的量子问题无法严格求解，而通常的近似方法如微扰方法也失效。本文的目的是对一类重要的二维双阱势，即轴对称双阱势,建立一个具有一定通用性的简化模型，并对薛定谔方程进行求解和分析，得出其能谱，并在此基础上进一步讨论了势垒的平均高度对能量本征值的影响。

1 模型的建立

一般的轴对称双阱势比较复杂，在仅考虑能级问题的时候，可以将轴对称双阱势近似看成一个内部含有势垒的二维无限深轴对称方阱势。即

(1)

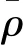
(2)

其中

(3)

为了确定强度K，利用内部势垒的体积不变，即模型与原型的体积相同条件

(4)

由此推出

(5)

考虑到势垒平均高度为

(6)

由此得到

(7)

(8)

这就是我们所给出的轴对称双阱势的简化模型。

2 模型的求解

2.1 定态薛定谔方程及其化简

在极坐标下，二维运动粒子的哈密顿算符为

(9)

在上述势阱中，对应的径向薛定谔方程为

(10)

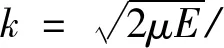
(11)

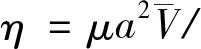
(12)

由于在V(ρ)→∞处波函数ψ→0，所以有齐次边界条件

R(ka)=R(ξ)=0

(13)

由于ρ=0为径向方程(10)的奇点，在该点波函数必须有界，所以有自然边界条件

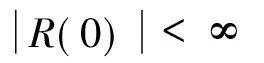
(14)

泛定方程(10)与边界条件(13)和(14)构成了确定能级的定解问题。

2.2 能级方程

显然，在x≠λξ处，泛定方程(10)成为

x2R″+xR'+[x2-m2]R=0

(15)

这是一个m阶贝塞尔方程[11]，其通解为

R=AJm(x)+BNm(x)

(16)

其中Jm(x)和Nm(x)分别为m阶贝塞尔函数和m阶诺依曼函数。将上式代入边界条件(13)和(14)两式，得到

(17)

此处略去了一个归一化因子。

在x=λξ处波函数连续，得到

AJm(λξ)=Nm(ξ)Jm(λξ)-Jm(ξ)Nm(λξ)=R(λξ)

(18)

但由于势阱中存在狄拉克势，在该处波函数的导数不连续，其跃变条件可以通过对方程(12)在x=λξ处的邻域积分得到

λ2ξ2[R'(λξ+0)-R'(λξ-0)]=λ2ξηR(λξ)

将(18)式代入上式，得到

ξ[Nm(ξ)Jm'(λξ)-Jm(ξ)Nm'(λξ)-AJm'(λξ)]=ηAJm(λξ)

(19)

如果Jm(λξ)≠0，上式可以消去系数A，得到

(20)

上式给出了以无量纲势垒位置λ、无量纲势垒高度η和磁量子数m为参数的能级方程，由此可以解出ξ=ξn(λ,η,m)，进一步推出能级

(21)

如果Jm(λξ)=0，则由Nm(ξ)Jm(λξ)-Jm(ξ)Nm(λξ)=0，即Jm(ξ)Nm(λξ)=0。解出无量纲变量ξ后代入(19)式，即可以求出待定参数A。

2.3 解的分析

当n足够大时，利用贝塞尔函数的渐近公式

得到

(22)

当η→∞时，中间势垒将两边的势阱分割为两个独立部分，产生了新的边界条件R(λξ)=0。由(18)式可知，两边的能级分别满足条件

Jm(λξ)=0,Nm(ξ)Jm(λξ)-Jm(ξ)Nm(λξ)=0

(23)

当n足够大时，利用柱函数的渐近公式得到

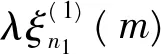
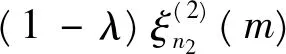
(24)

3 能级的数值结果

将贝塞尔函数和诺依曼函数的具体形式代入能级公式，再进行数值计算，就可以得到能谱。

下面，我们以磁量子数m=0为例，来进行具体计算。利用柱函数的递推公式

Zm'-mZm/x=-Zm+1

立刻得到Z0'=-Z1，能级方程(20)简化为

(25)

上式可以进一步简化为

ξJ0(ξ)[J1(λξ)N0(λξ)-J0(λξ)N1(λξ)]

=-ηJ0(λξ)[J0(λξ)N0(ξ)-N0(λξ)J0(ξ)]

(26)

下面我们具体考虑给定势垒位置，不同势垒高度的情况。

不失一般性，假定λ=0.5，用科学计算软件Mathematica来求解，结果如下：

表1 不同势垒高度时前5个能级的数值结果

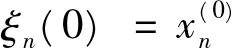
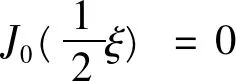
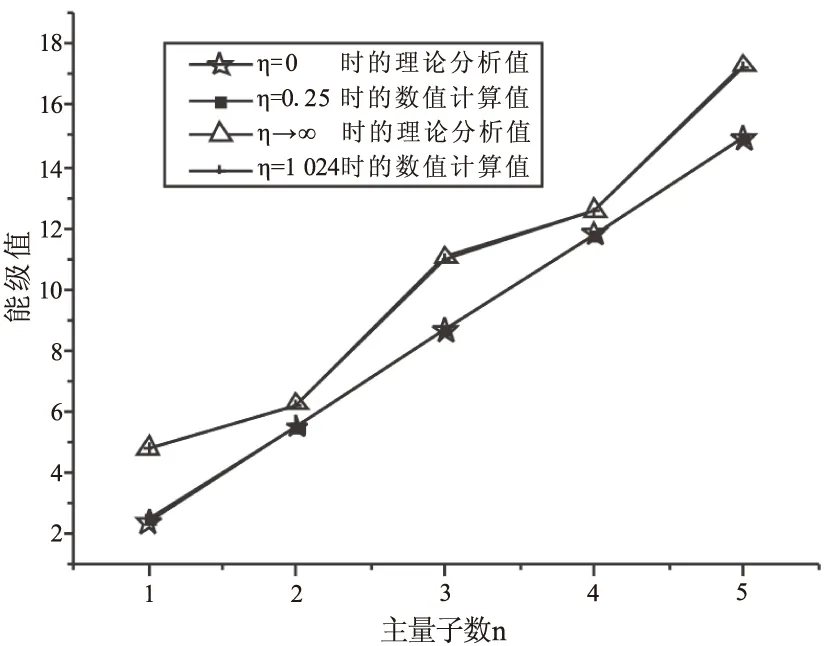
图1 势垒取极限值时能级的理论分析值与数值计算结果的比较

如图1所示，将势垒取极限值时能级的理论分析值与数值计算的结果进行比较可以发现，两者具有很好的一致性。

由此我们发现，模型的能级随着势垒高度的增加而增加，最后趋向于一个确定的极限值，这个极限值就是前面我们在极限分析中所得到的结果。进一步的数值计算表明，如果取不同的磁量子数或者势垒位置，也得到同样的规律。

4 结论

本文提出了轴对称双阱势的一个简化模型，并对该模型中的束缚态能级问题进行了理论分析，得到了严格的能级方程。在此基础上，利用Mathematica进行了数值计算，并讨论了势垒的平均高度对能量本征值的影响。我们发现，随着平均势垒高度的增加，能级的值也在不断增加，最后趋向于一个确定的极限值。

[1] 郑伟谋，刘寄星．量子双阱势准确解模型[J]．物理学报，1985，34(12)：1658-1665．

[2] 袁德荣．一种可能的超导孤子通道:带有非对称双阱势的氢键链[J]．湖北大学学报(自然科学版)，1999，21(3)：239-243．

[3] 朱文熙，王玉平．对称双方势阱能级无简并[J]．大学物理，1999，2(2)：33-34．

[4] 朱 涛，刘克家，王金凤．一种光滑连续双势阱模型的精确求解[J]．贵州工业大学学报(自然科学版)，2003，32(6)：14-17．

[5] 曹冬梅，李永放，王利强．静电场作用下非对称双势阱中本征问题的研究[J]．陕西师范大学学报(自然科学版)，2006，34(4)：37-40．

[6] 房永翠，杨志安，杨丽云．对称双势阱玻色-爱因斯坦凝聚系统在周期驱动下的动力学相变及其量子纠缠熵表示[J]．物理学报，2008，57(2)：661-666．

[7]XiaoKW,HaiWH,LiuJ.Coherentcontrolofquantumtunnelinginanopendouble-wellsystem[J].PhysicalReviewA, 2012, 85(1): 013410.

[8]ZhouXF,ZhangSL,ZhouZW,etal.Bose-Einsteincondensatesinaring-shapedtrapwithanonlineardouble-wellpotential[J].PhysicalReviewA, 2012, 85(2): 023603.

[9]CartariusH,WunnerG.ModelofaPT-symmetricBose-Einsteincondensateinadelta-functiondouble-wellpotential[J].PhysicalReviewA, 2012, 86(1): 013612.

[10]ChenBH,WuY,XieQT.Heunfunctionsandquasi-exactlysolvabledouble-wellpotentials[J].JournalofPhysicsa-MathematicalandTheoretical, 2013, 46(3): 035301.

[11] 倪致祥．数学物理方法[M]．合肥：中国科学技术大学出版社，2012：151-157．

Theenergylevelofasimplifiedmodeloftheaxisymmetricdoublewellpotential

QUKui，NIZhi-xiang

(SchoolofPhysicsandElectronicEngineering,FuyangNormalUniversity,FuyangAnhui236037,China)

Asimplifiedmodeloftheaxisymmetricdoublewellpotentialhasbeenintroduced.ThewavefunctionandenergyeigenequationaregainedfromthestrictsolutionofSchrodingerequation.NumericalcalculationhasbeendonebyusingMathematica.Theinfluenceoftheaverageheightofthebarrierontheenergyeigenvalueisdiscussed.Theresultsshowthatwiththeincreaseoftheaverageheightofthebarrier,thevalueoftheenergyisalsoincreasing,andfinallytendstoacertainlimitvalue.

axialsymmetry;doublewellpotential;dpotentialbarrier;energyeigenvalue

2015-08-06

国家自然科学基金项目(11273008)；安徽省教学团队项目(20100636)；阜阳师范学院质量工程项目(2014JXJD01)资助。

屈 奎(1982-)，硕士，讲师，研究方向：分子与原子物理。

O413.1

A

1004-4329(2015)04-038-04

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-038-04