基于数值及形状相似度的火炮动力后坐模拟准确度评估
第一作者杨玉良男,博士生,1987年生
通信作者秦俊奇男,教授,博士生导师,1961年生
基于数值及形状相似度的火炮动力后坐模拟准确度评估
杨玉良1,秦俊奇1,狄长春1,孙也尊2,李小卫3(1.军械工程学院火炮工程系,石家庄050003; 2. 北京军代局驻二四七厂军代室,太原030009;3. 66036部队保障处,河北邯郸056106)
摘要:火炮动力后坐试验装置通过高速冲击头撞击炮口推动火炮后坐,为新型后坐模拟试验方法。为分析该试验方法模拟后坐的准确度,通过实弹射击试验及基于试验装置的模拟射击试验,获取两种射击条件下后坐位移及速度时间序列;用时间序列相对误差的加权均值表征数值相似度,据时间序列曲率误差值求取形状相似度,据时间序列的曲率距离法求取形状相似度,并基于多属性指标评价理论计算综合相似度,进而对试验装置的后坐模拟准确度进行评估。该研究可为试验装置用于靶场试验提供理论依据。
关键词:火炮动力后坐;曲率;准确度评估;数值相似度;形状相似度
收稿日期:2014-10-16修改稿收到日期:2014-12-12
中图分类号:TJ306+.1文献标志码:A
Accuracy assessment of gun-power-recoil simulation based on numerical value similarity and shape one
YANGYu-liang1,QINJun-qi1,DIChang-chun1,SUNYe-zun2,LIXiao-wei3(1.Department of Artillery Engineering, Ordnance Engineering College, Shijiazhuang 050003, China;2.Beijing Military Delegation Office at Fact. 247, Taiyuan 030009, China;3. Department of Support, PLA Unit of 66036, Handan 056106, China)
Abstract:Gun-power-recoil test machine is a new-fashioned recoil simulation test machine with a high-speed mass impacting the muzzle of a gun to promote gun recoil. In order to analyze the recoil simulation accuracy of the test method, through actual firing tests and simulation firing tests based on the test machine, the gun’s recoil displacement and recoil velocity time series under the two firing conditions were obtained. The numerical value similarity was characterized by the weighted average value of relative error of time series. Shape similarity was calculated by curvature distance of time series. The shape similarity was calculated with the curvature relative error of time series. The comprehensive similarity was calculated based on the multi-index evaluation theory, and the recoil simulation accuracy of the test machine was evaluated. The study results provided a theoretical basis for the application of the gun-power-recoil test machine in the target.
Key words:gun-power-recoil; curvature; accuracy assessment; numerical value similarity; shape similarity
实弹射击试验是检验火炮装备可靠性的重要手段。为节约研制、试验经费,减少试验周期,自上世纪50年代开始寻求等效的火炮动力后坐模拟试验技术、研制试验装置[1-2]。试验模拟准确度会直接影响能否用于靶场试验鉴定。本文以某新研制的火炮动力后坐试验装置为研究对象,结合实弹射击数据及基于该装置模拟射击数据,将两组数据考虑为时间序列,通过计算时间序列数值及形状相似度对试验装置后坐模拟准确度进行评估。数值相似度一般通过计算两个时间序列间距衡量相似性。常用计算公式有曼哈坦距离、欧式距离、明可夫斯基距离等,在此基础上结合文献[3],采用两时间序列相对误差的加权均值表示数值相似度。
形状相似度算法包括时间弯曲距离法[4]、斜率距离法[5]、弧度距离法[6]、曲率距离法[7]、Prony变换法[8]、规范系数法[9]等。其中,时间弯曲距离法计算量过于庞大;斜率距离法、弧度距离法以时间序列中相邻两点间线段呈现的几何性质为依据对序列进行相似性度量,只反映序列相邻时刻信息之关系,对整个序列信息表达具有局限性;Prony变换法通过提取时间序列对应曲线的频率、阻尼、能量、相位等特征进行相似度分析,但不适用于分析强非线性曲线;规范系数法在试验数据有一定噪声波动时易产生计算误差,影响评估结果;曲率距离法能充分体现序列连续时刻信息间关联性,且具有降噪性、直观性、平移旋转不变性等优点[10]。本文采用曲率距离法求取时间序列的形状相似度。
1火炮动力后坐模拟试验方法
实弹射击时火药燃烧产生高压气体,进而推动火炮后坐,作用于身管轴线方向的炮膛合力Fpt即为主动力
(1)
式中:mh为后坐部分质量;X为后坐行程;t为后坐时间;Fpt为炮膛合力;FR为后坐阻力。
基于试验装置进行模拟射击,工作原理见图1。试验装置由液压动力系统、冲击系统及被试件三部分组成。被试件即火炮后坐部分,冲击头在液压动力系统推动下加速运动,达一定速度后冲击头与液压动力系统脱离,高速撞击火炮炮口,推动火炮后坐。推动火炮后坐的主动力为冲击头撞击炮口产生的冲击力Fn,即
(2)
即冲击力Fn替代炮膛合力Fpt发挥与火药燃烧相似的瞬间爆发、推动作用,通过调整冲击头质量、速度及波形发生器的刚度、阻尼值,使冲击力与炮膛合力基本吻合。
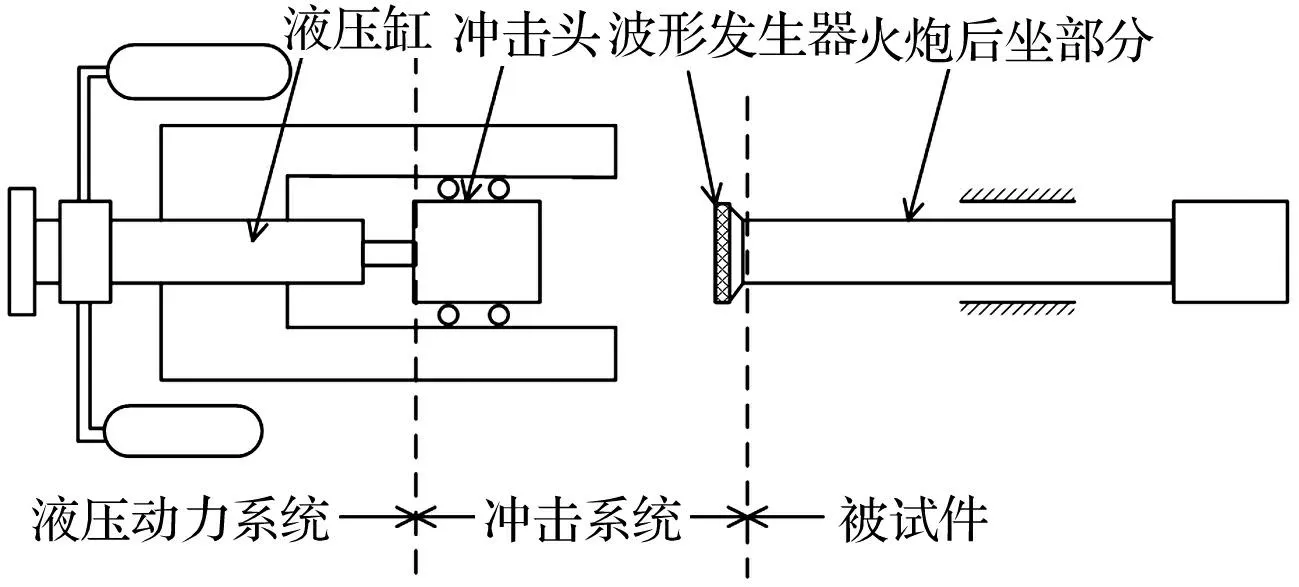
图1 试验装置冲击原理图 Fig.1 Schematic diagram of test machine impact
2实弹射击与模拟射击试验
在武器试验靶场对某型火炮进行实弹射击试验,试验条件为全装药、常温、6°射角。用位移传感器测试射击过程火炮后坐位移,并通过求导获得后坐速度曲线。用国内某研究所的火炮动力后坐试验装置,将火力系统安装在试验装置上。火力系统包括后坐部分(含身管、炮尾及反后坐装置后坐部分)、炮架、高低机、方向机、平衡机、炮塔、座圈等。火炮后坐部分质量1.2 t,实弹射击试验中最大后坐速度为16 m/s,考虑动量守恒,冲击头质量、速度均应与火炮后坐部分相同,此时能量传递率最高。试验装置提供的冲击头最大速度为15 m/s,小于实弹射击,且考虑冲击过程中能量损失,冲击头质量定为1.5 t,冲击头速度为15 m/s。选定波形发生器材料类型,对该火炮进行模拟射击试验。实弹射击与模拟射击试验均进行三次,对测试数据取平均值,获得实弹射击及模拟射击条件下后坐位移及速度曲线,见图2、图3。
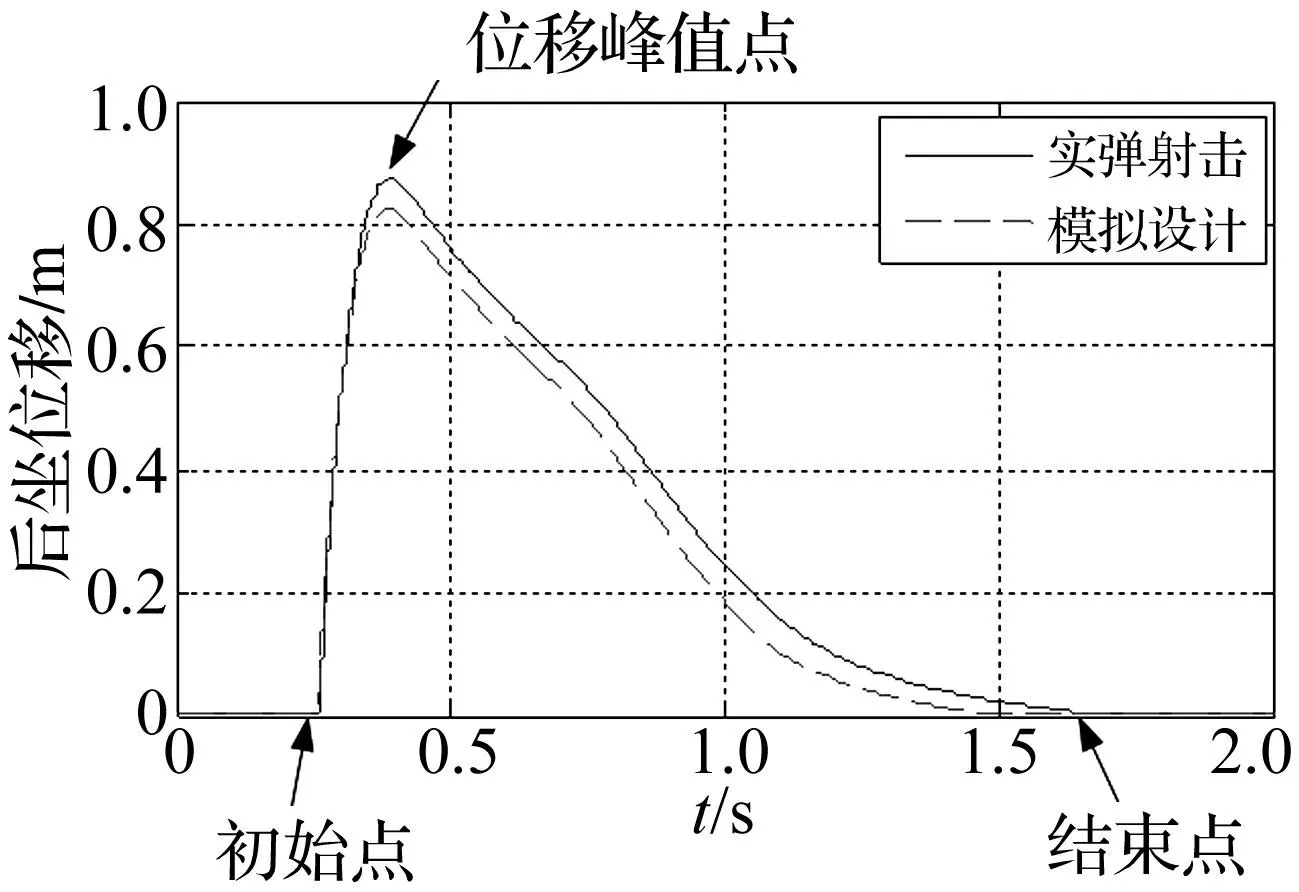
图2 后坐位移对比 Fig.2 Comparison of recoil displacement
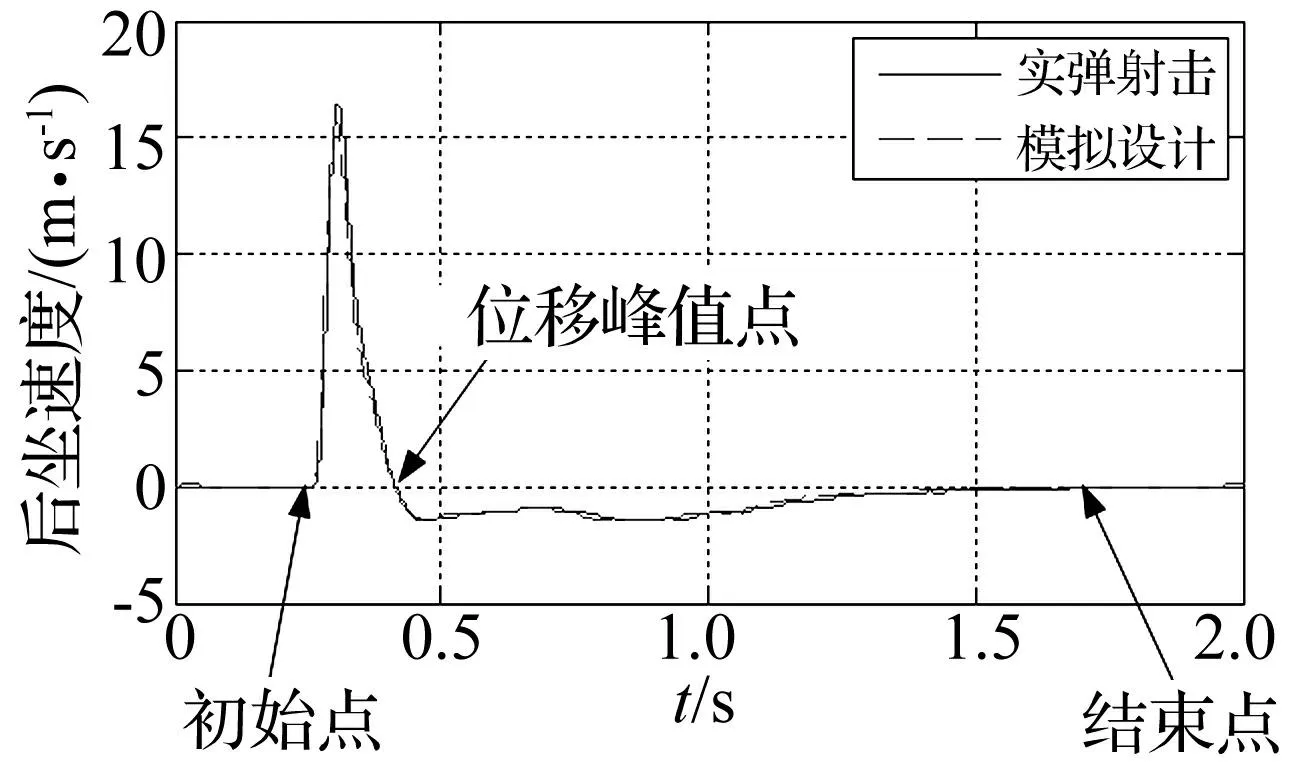
图3 后坐速度对比 Fig.3 Comparison of recoil velocity
3相似度评估算法
在以上数据基础上,采用基于数值及形状相似度算法对试验装置后坐模拟准确度进行评估,流程见图4。
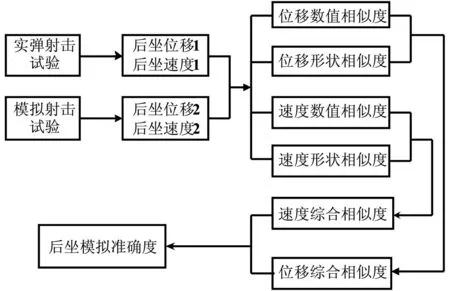
图4 评估算法流程图 Fig.4 Evaluation algorithm flowchart
3.1数值相似度
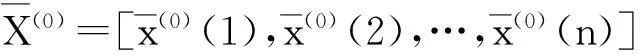
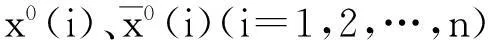
(3)
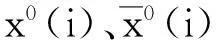
(4)
以每点幅值与全部采样点幅值和的比值作为该点权重γi,即
(5)
则两时间序列的整体数值相似度S1为
(6)
3.2形状相似度
根据两时间序列取曲率距离求取形状相似度,计算步骤如下:
(1)时间序列正向平移。将原序列X(0)=[x(0)(1),x(0)(2),…,x(0)(n)]转化为非负序列X(1),且保证序列形状不变,变换方法为
(7)
(2)时间序列分段表示。为提高时间序列拟合模型精度、减少计算量,需对非负序列进行分段处理,即
X(1)=[X1(1),X2(1),…,Xm(1)]
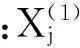
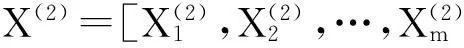
(8)
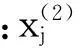
(9)
由式(8)、(9)看出,序列X(1)与X(2)可相互转化,且X(2)反映出X(1)中信息的变化规律,故可通过对X(2)建模分析X(1)。
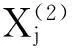
(10)
式中:ci(i=1,2,…,5),α为模型参数;p=1,2,…,lj。
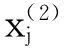
(5)时间序列的曲率表示。设拟合时间序列各段曲率为K=[K1,K2,…,Km],各子序列曲率为Kj=[kj(1),kj(2),…,kj(lj)],则
(11)
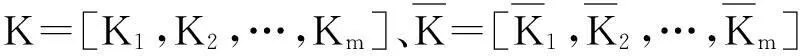
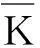
(12)
设定两个子序列的曲率距离阈值thDC,当曲率距离小于阈值thDC时,则称两个子序列相似,反之当曲率距离大于阈值thDC时,则称两个子序列不相似,其中阈值thDC的选取与每段子序列中各点曲率相关。
利用所有相似子序列的长度与序列总长度的比值作为序列形状相似度的度量。
(13)
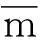
3.3时间序列综合相似度
据两时间序列分别计算数值相似度及形状相似度。基于多属性指标评价理论,两相似度属性用乘法关系较用加法关系求取综合相似度更合理。故实弹射击与模拟射击试验数据序列综合相似度S为
(16)
式中:S1,S2分别为数值及形状相似度。
4模拟准确度评估
据火炮后坐运动过程,将后坐时间数据序列分为后坐段及复进段两个长时子序列。整个时间序列从初始点到结束点,后坐段从初始点到位移峰值点,复进段从位移峰值点到结束点。后坐段中,火炮运动速度快、振动较剧烈,且最大速度出现在该段中;复进段中火炮速度较慢、振动较小,故两段长时子序列权重分别取0.6、0.4。
将两长时子序列划分为多个短时子序列,每段短时子序列长度为10。按以上方法计算每段短时子序列数值及形状相似度,进而推算长时子序列、整个序列数值及形状相似度。结合两种射击条件的后坐数据,计算出后坐位移、速度值及形状相似度见表1、表2。表中子序列1代表后坐段,2代表复进段。结合两表数据,据式(16),计算出两种射击条件下后坐位移的综合相似度为0.860 7,后坐速度的综合相似度为0.803 9。由两表看出,数值相似度大于形状相似度计算结果,综合相似度介于两者之间,考虑数值、形状两方面对相似度影响,计算的结果更合理。

表1 后坐位移相似度

表2 后坐速度相似度
后坐位移与后坐速度两时间序列在模拟准确度评估中均较重要,主次相当,故权重系数均取0.5,获得火炮动力后坐试验装置的后坐模拟准确度为0.832 3。评估结果表明,该试验装置能较准确模拟火炮实弹射击的动态过程。因此,通过对试验装置进行参数优化设计,可提高模拟准确度,更广泛用于火炮装备试验及验收。
5结论
针对火炮动力后坐试验装置的模拟准确度评估问题,采用基于数值及形状相似度的评估算法进行了分析,并得出其整体相似度为0.8323。
根据火炮的后坐运动过程,将其分为后坐及复进两个阶段,并分别赋予权重为0.6、0.4。计算两时间序列相对误差的加权均值求取数值相似度,并考虑了时间序列中数值出现零的情况;根据两时间序列的曲率距离求取形状相似度,采用乘法关系求取综合相似度。本文为试验装置后坐模拟准确度评估提供了理论依据,同时该方法也推广到其它装置,为分析及研究时间序列相似度提供了一定的方法参考。
参考文献
[1]姚养无. 火炮后坐仿真试验系统及其动力学数值仿真[J]. 兵工学报, 2001, 22(2): 152-155.
YAO Yang-wu. Simulation test system of gun recoil and numerical calculations[J]. Acta Armamentarii, 2001,22(2):152-155.
[2]杨玉良,秦俊奇,狄长春,等. 火炮动力后坐试验台波形发生器优化设计研究[J]. 振动与冲击, 2014, 33(2): 47-51.
YANG Yu-liang, QIN Jun-qi, DI Chang-chun, et al. Optimization design on waveform generator of gun- power-recoil test machine[J]. Journal of Vibration and Shock, 2014, 33(2): 47-51.
[3]周成,贺仁睦. 应用界标分界法的电力系统动态仿真准确度评估[J]. 中国电机工程学报, 2010,30(7): 42-47.
ZHOU Cheng, HE Ren-mu.Accuracy assessment of power system dynamic simulation based on landmark method[J]. Proceedings of the CSEE, 2010,30(7): 42-47.
[4]肖辉,胡运发. 基于分段时间弯曲距离的时间序列挖掘[J]. 计算机研究与发展, 2005, 42(1): 72-78.
XIAO Hui, HU Yun-fa. Datamining based on segmented time warping distance in time series database[J]. Journal of Computer Research and Development,2005,42(1): 72-78.
[5]梁建海,张建业,杨峰,等. 时间序列度量的斜率偏离距离方法研究[J]. 计算机工程与应用, 2009, 45(22): 4-6.
LIANG Jian-hai, ZHANG Jian-ye, YANG Feng, et al. Study of distance-measuring method in time series based on slope departure[J]. Computer Engineering and Applications, 2009, 45(22): 4-6.
[6]丁永伟,杨小虎,陈根才,等. 基于弧度距离的时间序列相似度量[J]. 电子与信息学报, 2011, 33(1): 122-128.
DING Yong-wei, YANG Xiao-hu, CHEN Gen-cai, et al. Radian-distance based time series similarity measurement [J]. Journal of Electronics & Information Technology, 2011, 33(1): 122-128.
[7]刘博宁,张建业,张鹏,等. 基于曲率距离的时间序列相似性搜索方法[J].电子与信息学报,2012, 34(9): 2200-2207.
LIU Bo-ning, ZHANG Jian-ye, ZHANG Peng, et al. Similarity search method in time series based on curvature distance[J].Journal of Electronics and Information Technology, 2012, 34(9): 2200-2207.
[8]高松,贺仁睦,马进. 电力系统动态仿真误差评定准则研究[J]. 电力系统自动化, 2006, 30(4): 6-10.
GAO Song, HE Ren-mu, MA Jin.Error criteria on power system dynamic simulation validation[J]. Automation of Electric Power Systems, 2006, 30(4): 6-10.
[9]周成,贺仁睦,王吉利,等. 电力系统元件模型仿真准确度评估[J]. 电网技术, 2009, 33(14): 12-15.
ZHOU Cheng, HE Ren-mu, WANG Ji-li, et al.Assessment on simulation accuracy of power system component model[J]. Power System Technology, 2009, 33(14): 12-15.
[10]王斐,梁晓庚,王艳奎,等. 基于曲率距离的制导系统动态仿真可信度评估[J].系统仿真学报,2013,25(8):1896-1900.
WANG Fei, LIANG Xiao-geng, WANG Yan-kui, et al. Credibility evaluation for guidance system dynamic simulation with curvature distance[J]. Journal of System Simulation, 2013, 25(8): 1896-1900.
[11]陈举华,郭毅之. GM模糊优化方法在小子样机械系统故障预测中的应用[J]. 中国机械工程, 2002, 13(19): 1658-1660.
CHEN Ju-hua, GUO Yi-zhi. Application of GM fuzzy optimal method in fault forecasting for a few sample mechanical systems[J]. China Mechanical Engineering, 2002, 13(19): 1658-1660.


