基于非线性气弹耦合模型的风力机柔性叶片随机响应分析

第一作者徐磊男，硕士生，1988年生

通信作者李德源男，博士后，教授，1965年生

基于非线性气弹耦合模型的风力机柔性叶片随机响应分析

徐磊1，李德源1，莫文威1，吕文阁1，刘雄2(1.广东工业大学机电工程学院，广州510006; 2.汕头大学能源研究所，汕头515063)

摘要：为准确模拟柔性叶片在紊流风速下的气弹响应，研究叶片振动对气动载荷与气弹响应的反馈,构建包含多体系统动力学模型与气动模型的柔性叶片非线性气动弹性力学模型。在将细长柔性叶片离散为多刚体系统基础上，运用计算多体系统动力学理论和Roberson-Wittenburg的建模方法，结合叶素动量理论，采用Kaimal模型模拟脉动风速，建立风力机柔性叶片的气弹耦合方程。算例以美国可再生能源实验室(NREL)研制的5MW近海风力机为研究对象，分析叶片的振动和叶根的挥舞与摆振力矩，研究柔性叶片振动对气动载荷影响。结果表明,叶片达到一定长度后，模拟风力机气弹响应问题时，其振动影响不可忽略。

关键词：风力机；气弹响应；气弹耦合；振动

基金项目：国家自然科学基金(51276043)；教育部高等学校博士点科研

收稿日期：2014-01-08修改稿收到日期：2014-11-10

中图分类号:TK83文献标志码：A

Random response analysis for flexible blade of a wind turbine based on nonlinear aero-elastic coupled model

XULei1,LIDe-yuan1,MOWen-wei1,LÜWen-ge1,LIUXiong2(1. School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China;2.Institute of Energy Science, Shantou University, Shantou 515063, China)

Abstract:In order to exactly model the aeroelastic response of a blade under turbulent flow and study blade vibration’s feedback on aerodynamic load and aeroelastic response, here a nonlinear aeroelastic mechanical model containing flexible blade multibody system’s dynamic model and an aerodynamic model was constructed. Through discreting a flexible slender blade into a multi-rigid-body system, the aeroelastic coupled equations of the blade were obtained by using the theory of computational dynamics of multibody system and Roberson-Wittenburg modeling method. In the coupled equations, the blade element-momentum theory (BEM) was used to calculate the aeroelastic load of the wind turbine blade and Kaimal model was used to calculate random wind speed. The time domain response of a 5-MW offshore wind turbine blade of the US. Renewable Energy Laboratory was calculated. The response included the vibration of the blade and the flapwise and edgewise bending moments at the blade root. The effect of the vibration of the flexible blade on the aerodynamic load was also studied. The results revealed that the effect of slender blade vibration can not be ignored when simulating the aeroelastic response of a wind turbine.

Key words:wind turbine; aeroelastic response; aeroelastic coupled; vibration

大型风力机叶片一般采用复合材料蒙皮，其外形尺寸不断增大，作为主要承受空气动力的构件，细长叶片的有限变形和振动对于风力机组气动力的影响以及由此引起的与叶片结构响应的耦合成为不能忽略的问题。寻求包含非线性变形效应的柔性叶片动力特性与气动弹性耦合的数值分析方法成为了风力机气弹分析的重要基础[1]。

对于风力机系统的力学建模，目前国内外常用的建模方法主要有多体系统方法 (Multibody Systems，MBS)、有限元方法(Finite Element Systems，FES)和连续系统(Continuous Systems，COS)方法等[2-4]。对于风力机叶片来说，COS方法所建立的偏微分方程组仅在特殊的、简单的几何结构和载荷下才可能求解，不太适合复杂系统的时域仿真；而FES方法具有较多的自由度，计算和分析成本较高，仅适合于静态载荷分析和微动力学分析；MBS方法是将实际的机械构件视为刚体，用有限的自由度导出系统动力学微分方程(组)，但当系统中柔性构件的变形对系统动力学行为产生较大影响时，该方法模拟的精度有限。混合多体系统(Hybrid Multibody System，HMBS)方法则考虑了系统中构件的柔性，适合于包含刚体和柔性体的复杂系统的力学建模，也适合于风力机叶片或整机的力学建模。

对于风力机叶片这种具有空间运动和弹性变形的构件，Rauh等[5-7]引入“超级单元”(Superelement)对其进行离散，以反映其弹性变形,将LW-50/750风力机中变形相对较大的构件(如风轮叶片和塔架)处理为柔性体，将变形相对较小的构件(如轮毂、机舱)处理为刚体，采用超级单元(无扭转自由度)对风力机的柔性构件进行离散，各刚体之间通过力元(弹簧和阻尼器)和铰连接。这样风力机系统可以用一离散的刚、柔混合多体系统来表示。采用超级单元(含扭转自由度)对600 kW风力机的柔性叶片及塔架进行离散处理，基于虚功原理导出了整机混合多体系统的拉格朗日方程的显式表达式并分析了整机的固有模态。使用HMBS方法建立了NM80风力机的力学模型，利用哈密顿原理导出了动力学方程；分析了超级单元个数及计算弹簧系数不同的方法对柔性件的固有频率和阻尼系数计算精度的影响。

对于叶片的空气动力计算，目前通过数值求解Navier-Stokes 方程的计算流体力学(Computational Fluid Dynamics, CFD)方法[8]，计算精度较高，但对于风力机叶片这种较大尺寸且旋转运动的构件，计算量较大，要实现实时的气弹耦合还有一定困难。在风力机气动载荷计算中，叶素动量理论(Blade Element-Momentum Theory, BEM)[9]计算结果较合理且求解快速，还可与其它非定常气动模型结合，已在GH BLADED等大多数风力机性能与气动分析软件中广泛应用。其它用于气动载荷分析的方法如广义动态尾流理论(Generalized Dynamic Wake Theory ,GDW)等[10]也逐渐受到关注。相比于BEM理论，GDW除了计算旋转平面到尾流的轴向诱导速度还考虑了尾迹效应，气动模型相对更复杂。

对于风力机叶片或整机的非线性气弹分析，近年来国内外学者也进行大量的研究工作。任勇生等[11-12]基于叶片的典型截面模型和ONERA非定常气动模型对风力机叶片挥舞/摆振非线性气弹系统的动力失速稳定性进行了研究。刘廷瑞等[13-14]运用连续梁模型，通过方程的线性化和Galerkin数值求解方法，对叶片的非线性气弹问题进行了研究。李映辉等[15]同样通过建立连续梁的偏微分方程，施加外部和内部的正弦激励，通过Galerkin数值分析方法，研究了叶片的非线性振动。Holierhoek[7]利用WOBBE程序研究了由失速和附着流引起的叶片挥舞-摆振不稳定性的可能性。Meng[10]则通过开发结构和气动接口程序实现了基于现有的非线性多刚体动力学程序(MBDyn[16])和空气动力学模块(AeroDyn[17])的耦合求解。Ahlström[18]则使用MSC.Marc建立Alsvik水平轴风力机的有限元模型用于计算其动力学响应；采用现有的基于BEM理论的空气动力学程序AERFORCE计算气动载荷，同时使用SOSIS-W软件来模拟不同的风场条件，实现了风力机的气弹耦合计算。Hansen[1]采用CFD方法计算了某风力机的风轮空气动力学，研究了上游方向风轮的尾涡形成过程及其对下游方向风轮的影响。

本文应用计算多体动力学理论，将柔性叶片离散为若干通过运动副联接的多体系统，基于动力学普遍方程导出了该系统的动力学方程的一般形式，编制了通用的动力学建模与仿真程序。该程序能根据用于描述系统拓扑构型的输入数据自动建立和数值求解受约束的系统动力学方程(微分-代数方程组)。通过对系统的脉冲响应与系统的传递函数分析，得到系统的动力特性。在叶片多体系统模型的基础上，结合BEM气动模型导出气弹耦合模型，在数值积分的每一时间步中,气动模型也能实时地根据叶片各刚体的广义坐标和广义速度计算出作用在叶片各刚体上的气动载荷，并将其反馈到叶片动力学微分方程中，从而实现叶片的非线性气弹耦合时域响应分析。

本文针对美国可再生能源实验室(NREL)研制的5MW变速恒频风力机叶片[19]，数值分析了叶片在紊流风速下挥舞、摆振与扭转振动和叶根力矩的时域响应，重点关注了柔性叶片的振动对其气动载荷的影响。相关研究在大型风力机叶片设计与优化以及保障风力机组的安全稳定运行具有重要应用价值和意义。

1柔性叶片的多体系统动力学建模

大型叶片由于其较大的展弦比，且外壳一般采用玻璃钢等复合材料制成，在气动与机械载荷作用下，叶片在垂直来流和沿来流方向产生较大的弯曲变形并伴随扭转变形，表现出较大的柔性，与气动载荷形成反馈。本文借助 “超级单元”的思想将叶片离散为通过带弹簧和阻尼器的万向节或转动铰相联接的多刚体系统[7]，每个超级单元包含四个刚体。这样，叶片的横向弯曲变形与扭转变形就可以用较少的自由度得到展现。结合现代计算技术，采用计算多体动力学中的R-W建模方法来建立叶片的多体动力学模型。

1.1超级单元模型和叶片的离散

对于叶片这种细长构件，见图1。将其离散为若干个超级单元。每个单元中，用B1和B2，B3和B4四个通过万向节连接的刚体来反映其在相互垂直面内的弯曲变形，其广义坐标为θ1,θ2,θ4,θ5；而扭转变形则由B2和B3间的旋转铰来反映，广义坐标θ3。刚体间的相对运动通过弹簧与阻尼器约束(如图中的Cy1～Cy3、Cz1～Cz3)。

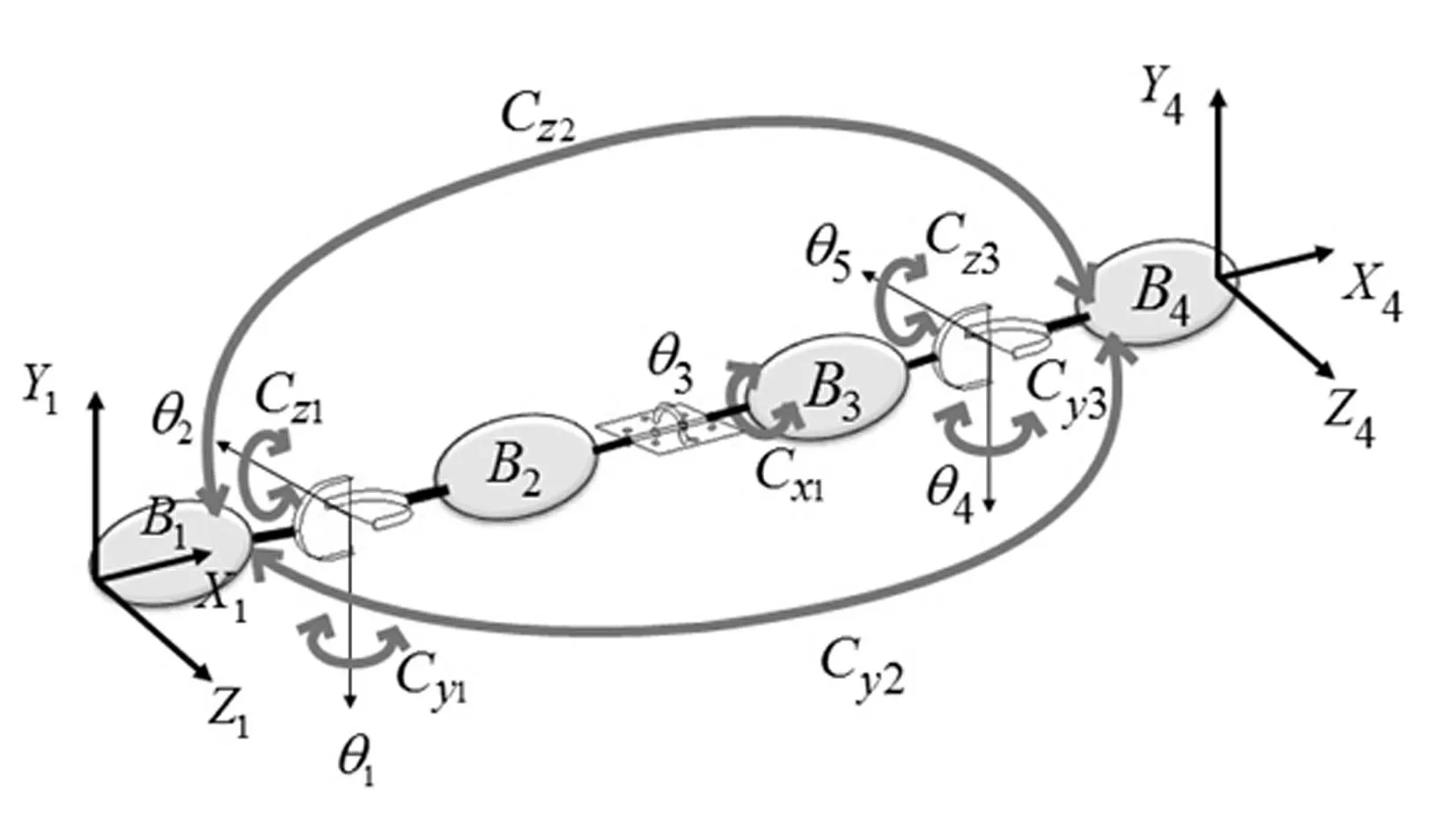
图1　超级单元模型 Fig.1 Superelement model

美国可再生能源实验室NREL推出的5MW近海风力机叶片长61.5 m，风轮直径125.0 m，本文将该叶片离散为4个超级单元，其中前后两个超级单元中相邻的刚体固结为一个刚体(如B4、B7和B10)，这样，整个叶片的拓扑构型为13个刚体组成的多体系统，共21个自由度，见图2。惯性坐标系为OXYZ(固定坐标系)，为方便考察叶片的挥舞和摆振方向的变形，建立叶根随动坐标系O′X′Y′Z′，OO′表示轮毂中心与叶根的距离，叶片绕固定坐标系的Z轴即风轮主轴的轴线转动。

1.2柔性叶片的多体系统动力学方程

R-W方法的特点是应用图论中的概念来描述多刚体系统，将系统中各对相邻刚体间的相对定位参数作为描述系统位形的广义坐标。如图2中对叶片多刚体系统进行规则标号，共有13个刚体(Bi,i=1,…,13)和内接铰(Hi,i=1,…,13)。除铰H1建立在定坐标系O点，其余内接铰Hi的铰点均建立在各刚体质心截面的气动中心(弦长1/4处)。体B1绕Z轴以风轮转速转动，即存在运动约束；内接铰Hi的相对运动可通过固结在体Bi及其内接体上的相对坐标系来描述。

图2　刚体规则标号、惯性坐标系XYZ和叶片坐标系X′Y′Z′ Fig.2 Regular mark number of each rigid body, inertial coordinate system XYZ and blade coordinate system X′Y′Z′

如上所述，可得叶片多体系统的广义坐标阵为

q(t)=(q1,…,q21)T

(1)

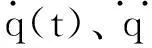
(2)

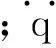
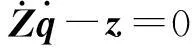
(3)

文献[20]中给出了广义质量阵Z、广义力阵z的具体表达形式和导出方法，由于篇幅所限，本文不再赘述。该方程组中，广义坐标q描述了刚体间的相对转动，由于柔性叶片较大的变形，这些量一般不为小量，不适合进行线性化，而且由于叶片的旋转，广义质量阵等随时间变化，即式(3)描述的是非线性、时变的系统。方程组的求解有一定困难，一般采用适当的数值积分方法结合相应的初始条件求得数值解。

1.3模型的相关参数与模型验证

叶片离散为多刚体系统，各刚体之间通过带弹簧和阻尼器的万向节或旋转铰连接。弹簧和阻尼器的设置是为了约束刚体间的相对转动，弹簧的刚度系数的取值应当使建立的叶片多刚体模型的力学特性与柔性叶片的尽量符合，一般应该满足：①在相同的静载荷作用下，叶片多刚体模型与原柔性叶片的弹性变形相同；②超级单元应与相同尺寸的刚性梁有相同的质量和惯性性质；③叶片多刚体模型的动力特性应尽量接近原柔性叶片的动力特性，如前若干阶固有频率、振型等相差满足要求的精度。

分析计算中涉及的叶片相关参数如沿叶片轴的刚度、质量分布，叶片截面几何参数以及与气动载荷计算相关的翼型翼型气动特性等参数可参考NREL发布的文献[19]。由于叶片的几何形状与力学特性可以用弹性梁来描述，参考文献[7]中列出了各超级单元中弯曲和扭转弹簧的刚度系数计算表达式。针对该5MW风力机叶片，计算得到的弹簧刚度系数见表1。在所建立的叶片多体模型基础上，通过施加脉冲激励，由频响函数(FRF)求得了该叶片的前5阶固有频率，该结果与应用多体动力学软件ADAMS对该叶片的分析结果以及NREL提供的分析结果进行了对比，结果见表2。

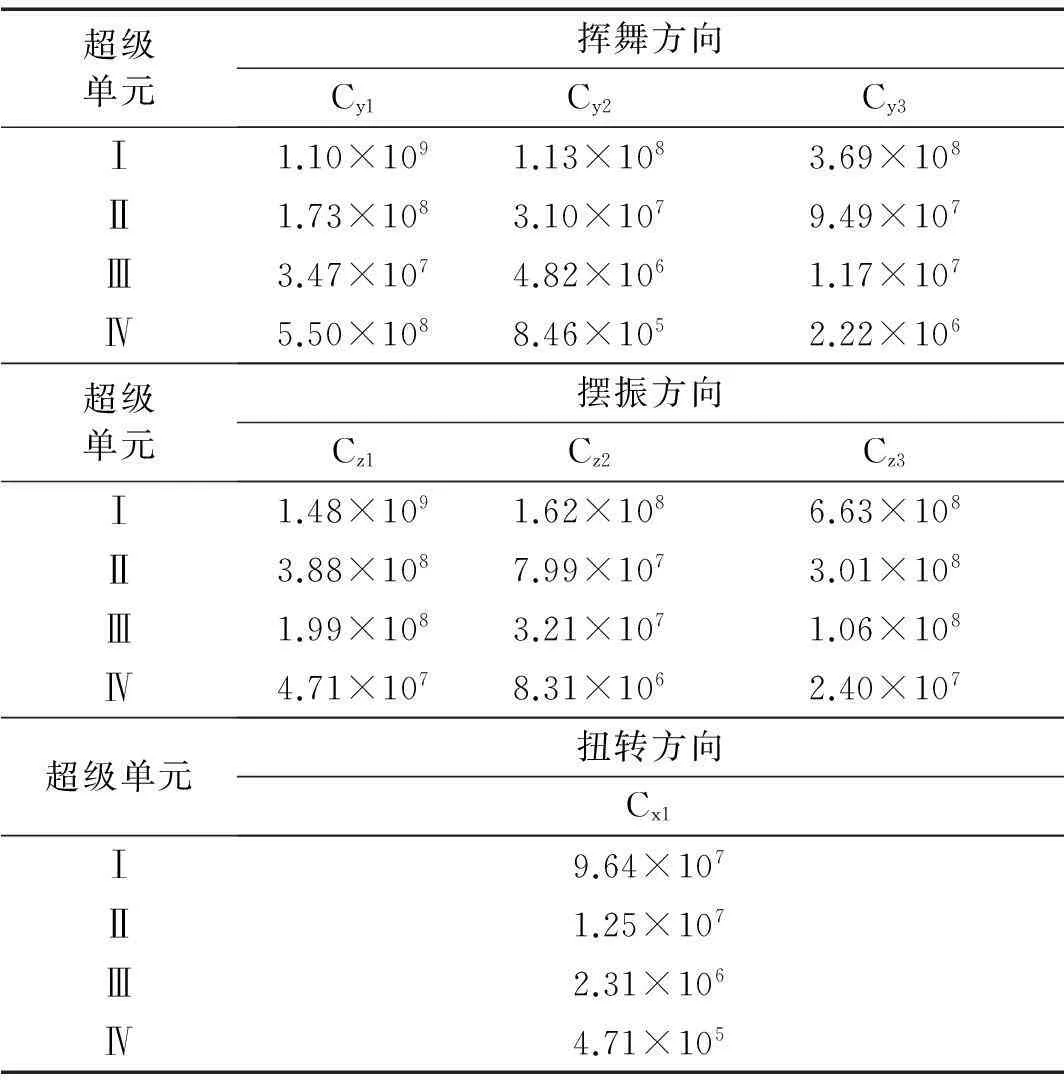
表1　NREL-5MW风力机叶片弹簧刚度系数/(Nm/rad)

表2　计算结果对比

注：单位为Hz,“—”表示没有数据

从表2可以看出，本文计算的叶片前5阶频率与NREL提供的结果基本吻合，表明文中的叶片离散模型与实际叶片的力学特性基本相同，质量、刚度分布也基本与实际相符；也证明了超级单元法能用较少的自由度准确地描述柔性叶片的弹性变形、气动载荷和叶片旋转运动间的耦合。结果也验证了仿真程序的有效性与叶片动力学模型的正确性。

2带约束项的柔性叶片多体动力学方程的建立及其数值求解

叶片在受力运动过程中，要受到各种几何或运动约束，如：控制系统所加的对风轮转速或主轴转矩的控制等，使得描述叶片多体系统位形的坐标q(t)=(q1,…,qn)T(n=21)相互不独立，若系统独立的约束方程个数为s个，即

Φ=(Φ1,…,Φs)T=0

(4)

则系统的独立的变量中只有δ=n-s个为独立的。结合前面导出的动力学方程(3)，得到带拉格朗日乘子叶片系统的动力学方程

(5)

式中：Φq为约束方程的雅克比s×n阶矩阵;σ=(σ1,…,σs)T为与约束方程对应的拉格朗日乘子阵;ΦTqσ表示刚体间所有理想约束力的贡献。此方程与约束方程(4)一起构成封闭的微分-代数方程组。

采用违约稳定方法求解(5)式与(4)式联合的微分-代数方程组，将全部广义坐标与拉格朗日乘子作为未知变量，方程组变为较大变量数的封闭方程。对违约现象进行修正，其思想在于对约束方程进行人工反馈[20]，方程为

(6)

式中:α,β为常数。适当选择这两个参数可保证Φ=0的解渐近稳定。将式(6)与式(5)组合成矩阵形式

(7)

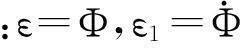
3叶片气动载荷计算与气弹耦合分析

作用在叶片上的随机空气动力的计算采用叶素-动量理论(BEM)，结合普朗特叶尖修正理论对气流绕叶尖的损失[8]。假设某刚体Bi(i=1,…,13)所受气动载荷沿叶片展向均匀分布，作用在叶片截面弦上距离前缘1/4即气动中心处,见图3。在叶素理论中，忽略气流沿叶片展向的流动，此时，作用在叶片旋转平面内某一环形区域上的推力FT及转矩Q为

FT=0.5BρcW2[CL(α)cosφ+CD(α)sinφ]L

(8)

Q=0.5BρcW2[CL(α)sinφ-CD(α)cosφ]Lr

(9)

进一步考虑气流的三维流动，根据动量理论，此时，环形区域所受的推力FT及转矩Q表达为

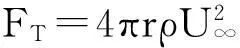
(10)

Q=4πr3ρU∞ω(1-a)a′FL

(11)

式中:c为Bi的质心截面处的弦长；W为相对风速，表示刚体Bi质心截面气动中心处的转速ωr与来流风速U∞的合速度；α为刚体Bi质心截面处的攻角；L为刚体Bi的长度；ρ为空气密度；CL、CD和CM分别是升力系数、阻力系数和力矩系数，由翼型特性与攻角确定；r为刚体Bi质心截面气动中心距离旋转中心的距离；B为风轮叶片数；ω为叶片转速；a、a′分别为轴向、切向诱导因子；F为普朗特叶尖损失因子。

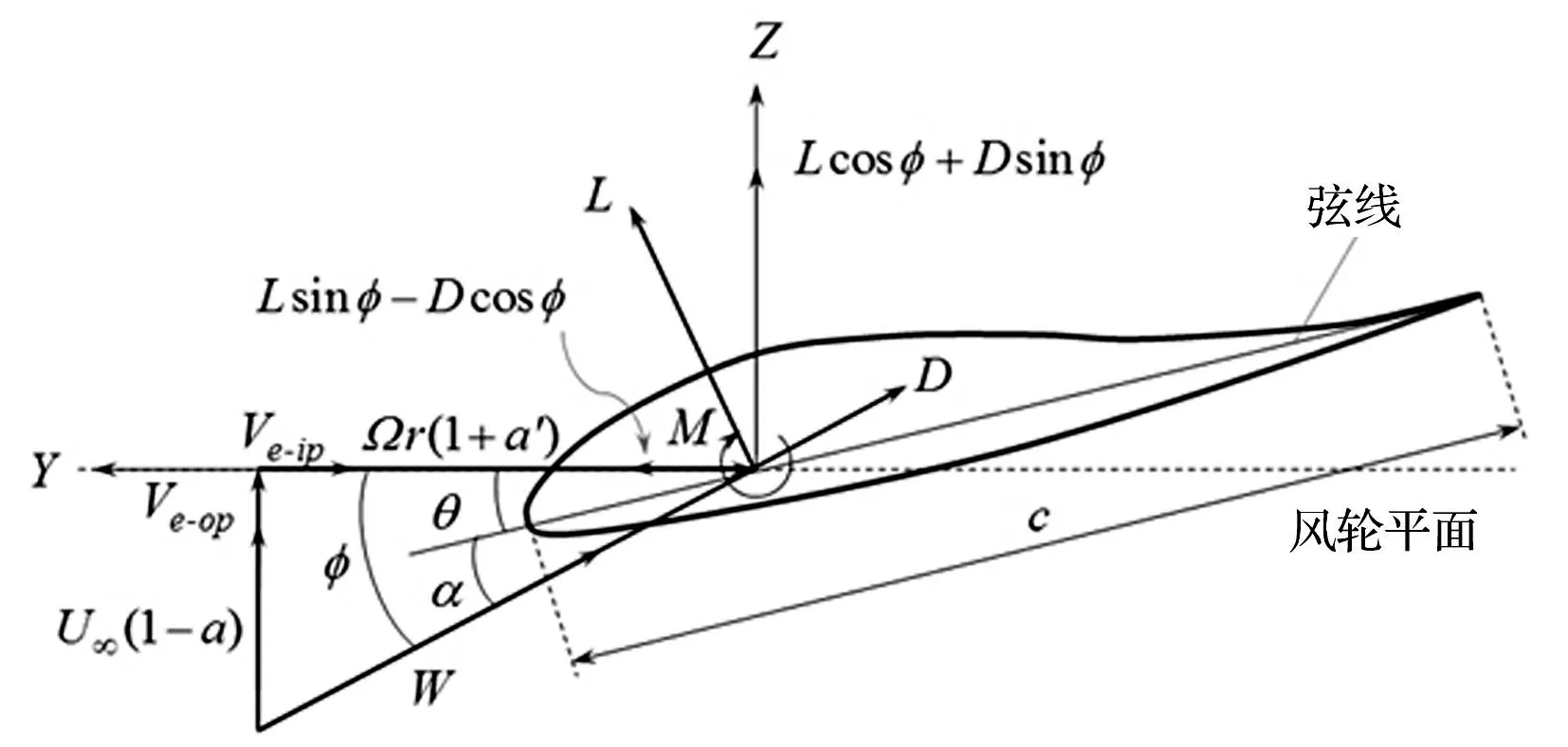
图3　刚体B i质心截面上的气动参数及气动中心连体基 Fig.3 Aerodynamic parameters on a CM cross-section of rigid body B iand body-fixed coordinate system aerodynamic center

本文研究的重点之一在于分析叶片变形对气动载荷的影响，这种影响体现在叶片挥舞与摆振速度对入流角φ及叶片扭转对攻角α的影响

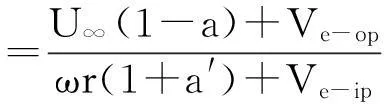
(12)

α=φ-θ

(13)

式中:φ为入流角(图3)；θ为叶片截面的扭转角；Ve-op、Ve-ip分别为气动中心挥舞与摆振速度。

应用以上表达式进行叶片气动载荷计算时，其中的轴向诱导因子a、切向诱导因子a′，以及入流角φ和攻角α需要根据翼型静态升、阻力数据通过迭代计算，具体迭代步骤见文献[21]。

叶片所受空气动力与其弹性变形的相互影响即气弹耦合分析流程见图4。图中显示了叶片多体系统动力分析模块与其气动载荷计算模块的耦合过程，在求解动力学微分方程数值积分的每一个时间步中，调用气动模块计算出该时刻的气动载荷，然后，这些载荷返回到数值积分模块，计算出下一时间步中各广义坐标与广义速度的值，这些参数再输入到气动模块，如此循环直到时间设定的仿真时间tend。

在本文的分析中，假设叶片以匀角速度绕主轴转动，为此建立约束方程

Φ=q1-ωet=0

(14)

式中:广义坐标q1为叶根刚体相对于主轴的转动;ωe为额定转速。如果叶片转速随风速变化，如变转速控制风力机，(14)式变为非线性约束方程。数值积分采用违约稳定法，取α=β=10，积分精度可视要求由分析者设定，本文算例仿真分析时取为10-5。

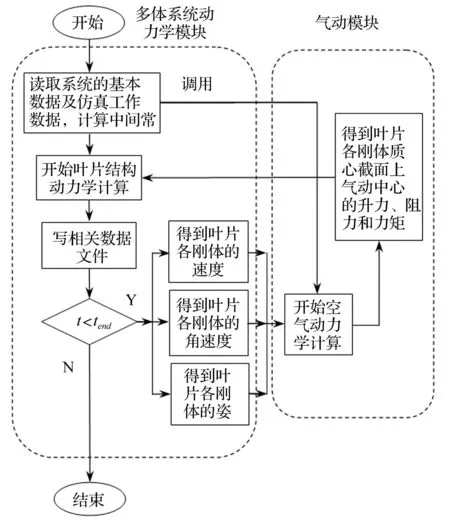
图4　气弹耦合分析流程图 Fig.4 Flow chart of aeroelastic coupling analysis

4紊流风场风速的模拟

从风力机风场大量实测风的数据可以知道，风速由两部分组成。第一部分是长周期部分，是大气宏观整体运动形成的，其周期一般在10 min以上，方向一般为水平纵向，大小只与高度有关；第二部分是短周期部分，是局部的紊流运动形成的，其周期只有几秒至几十秒。那么对于实际风场，风力机风场模型可分为稳态风和脉动风。

根据统计大量的风速实测样本可知，脉动风是零均值平稳的随机过程。可以采用自回归(Auto-Regressive，AR)模型模拟风速时程，那么M个点空间相关脉动风速时程过程[V(t)]=[V1(t),…,VM(t)]T可由下式生成

(15)

式中:[V(t-kΔt)]=[V1(t-kΔt),…,VM(t-kΔt)]T；[ψk]为AR模型自回归系数矩阵，M×M阶方阵；k=1,…,p，p为AR 模型的阶数；Δt为时间步长；N(t)为独立随机过程向量。

模拟风速时程的问题归结为回归系数矩阵[ψk]的求解、给定随机方差[N(t)]的求解和AR模型阶数的确定。具体分析过程见文献[22]。

风速谱采用Kaimal谱。该谱考虑了脉动风速功率谱随高度的变化，其纵向脉动风速功率谱表达式为

(16)

式中:f=nz/V(z)，V*=KV(z)/ln(z/z0),K≈0.4，V*为摩擦风速，V(z)为距地面高度z处的平均来流风速[22]。

频率取样点数取N=512，时间间隔Δt=0.1s，风速模拟时间为50 s，AR模型阶数p=4。5 MW大型水平轴风力发电机轮毂高度为90 m，图5为轮毂中心平均风速V(z)=11.4 m/s时中心处随机紊流风速时程曲线。

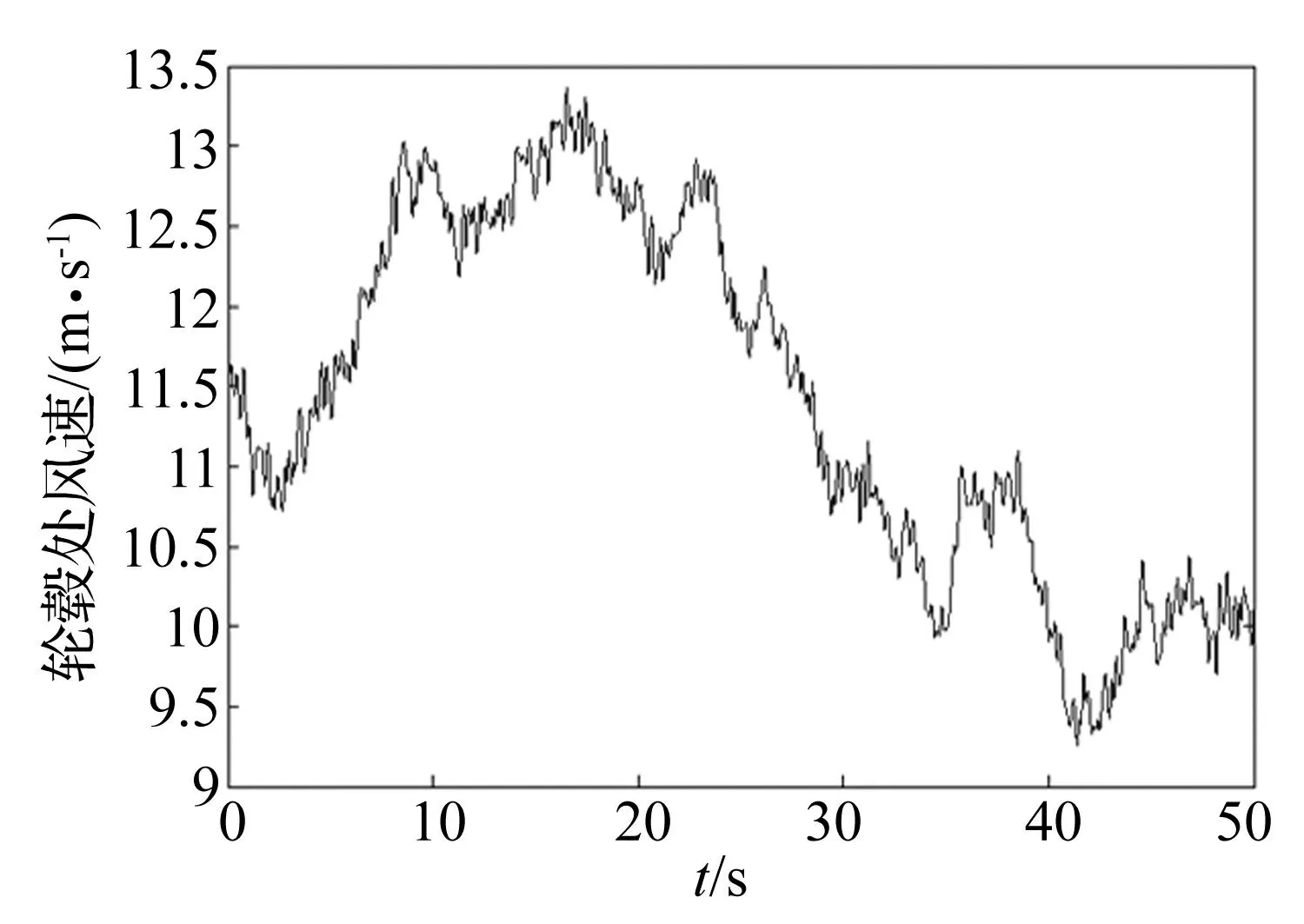
图5　轮毂处风速时间历程曲线 Fig.5 The time history curves of wind speed at the hub

5算例分析

5.1模型及其参数的选取

基于以上的建模基础，对文献[19]提供的5 MW风力机叶片在随机风速下的气弹响应进行了数值分析。计算过程在随机风速及额定转速(12.1 r/min)下进行。

考虑到此风轮直径(126 m)较大，叶片上各刚体(叶素)在不同的高度风速存在风剪，引入风速随高度变化的公式加以修正

(17)

式中:V,V0为距地面高度分别为H及H0处的平均风速。本文取V0=11.4 m/s，为轮毂高度H0=90 m处的风速；α为切变系数或粗糙度指数，是一个经验指数，其值为0.125～0.6，文中取0.16。

5.2叶片的气弹响应分析

图6中(a)和(b)分别为叶根的挥舞和摆振角加速度。由于叶片挥舞方向的弹簧刚度系数比摆振方向小，故叶片挥舞角加速度明显比摆振角加速度大。虽然模拟风速的瞬时波动会迅速加剧叶片的振动(如图6(b)中，摆振角加速度在35 s附近突然增大，这与图5中的模拟风速在该时刻迅速增加有关)，但从整体趋势来看，结构阻尼的存在使得叶片在这两个方向的角加速度慢慢地减少。

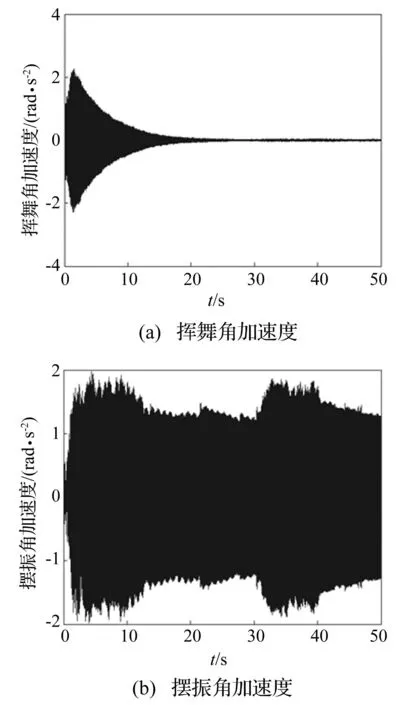
图6　 叶片挥舞角加速度和 摆振角加速度的时间历程曲线 Fig.6 The time history curves of flapwise and edgewise angular acceleration

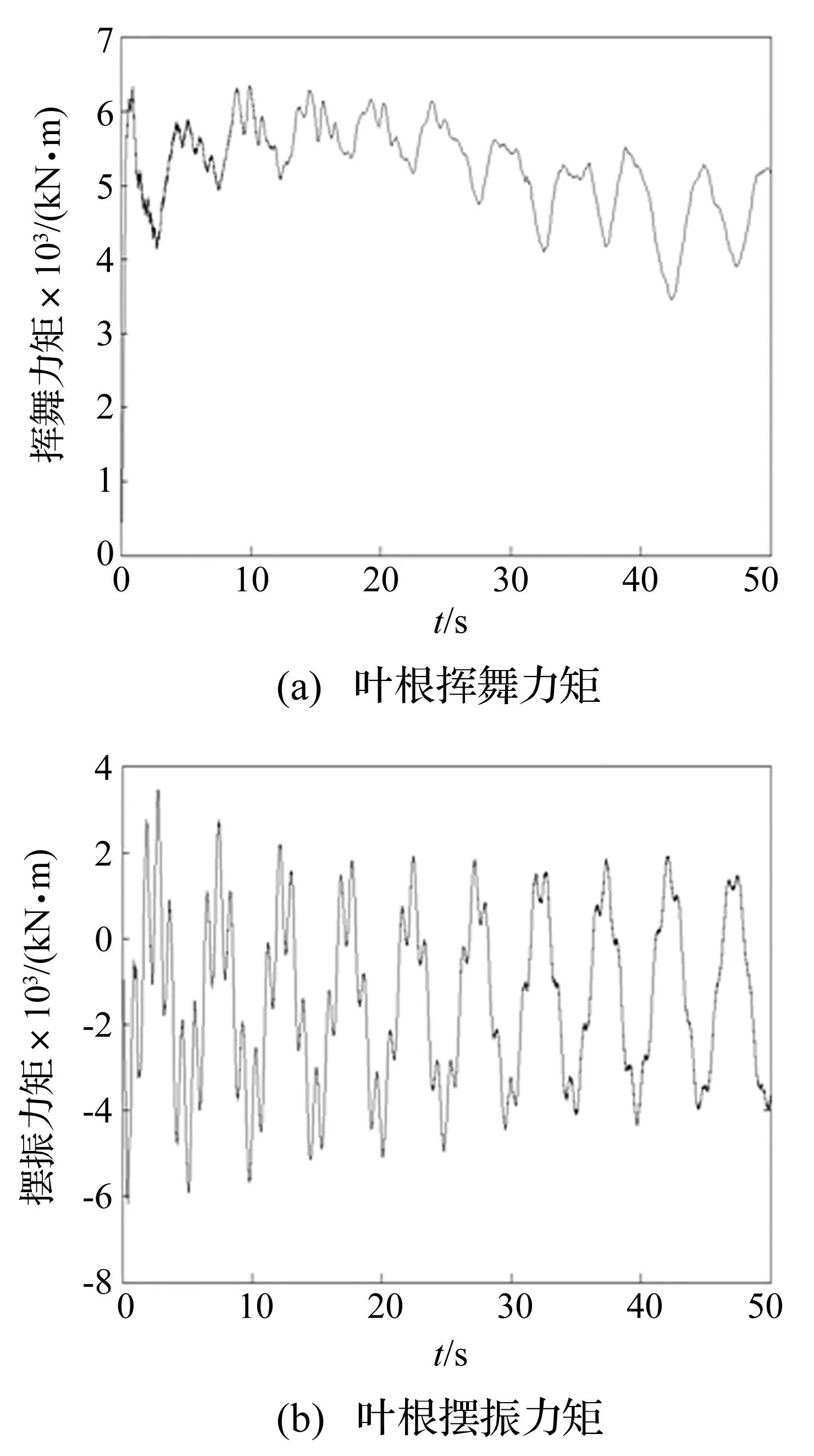
图7　叶根挥舞和摆振力矩时间历程曲线 Fig.7 The time history curves of flapwise and edgewise bending moment at the blade root

图7的(a)和(b)图分别为叶片叶根处的挥舞力矩和摆振力矩随时间变化曲线。在气动推力的持续作用下，叶根处承受着较大的挥舞力矩，均值约为5×106N·m。而在摆振方向，叶根同样承受着较大的力矩(约2×106N·m)，其中一部分来自于气动切向力产生的气动力矩，而主要部分则来自于叶片的自重。叶片在旋转过程中，叶片重力的方向会周期性地改变，导致叶片的摆振力矩变化幅度比挥舞力矩大，所以叶根处很容易产生疲劳破坏。

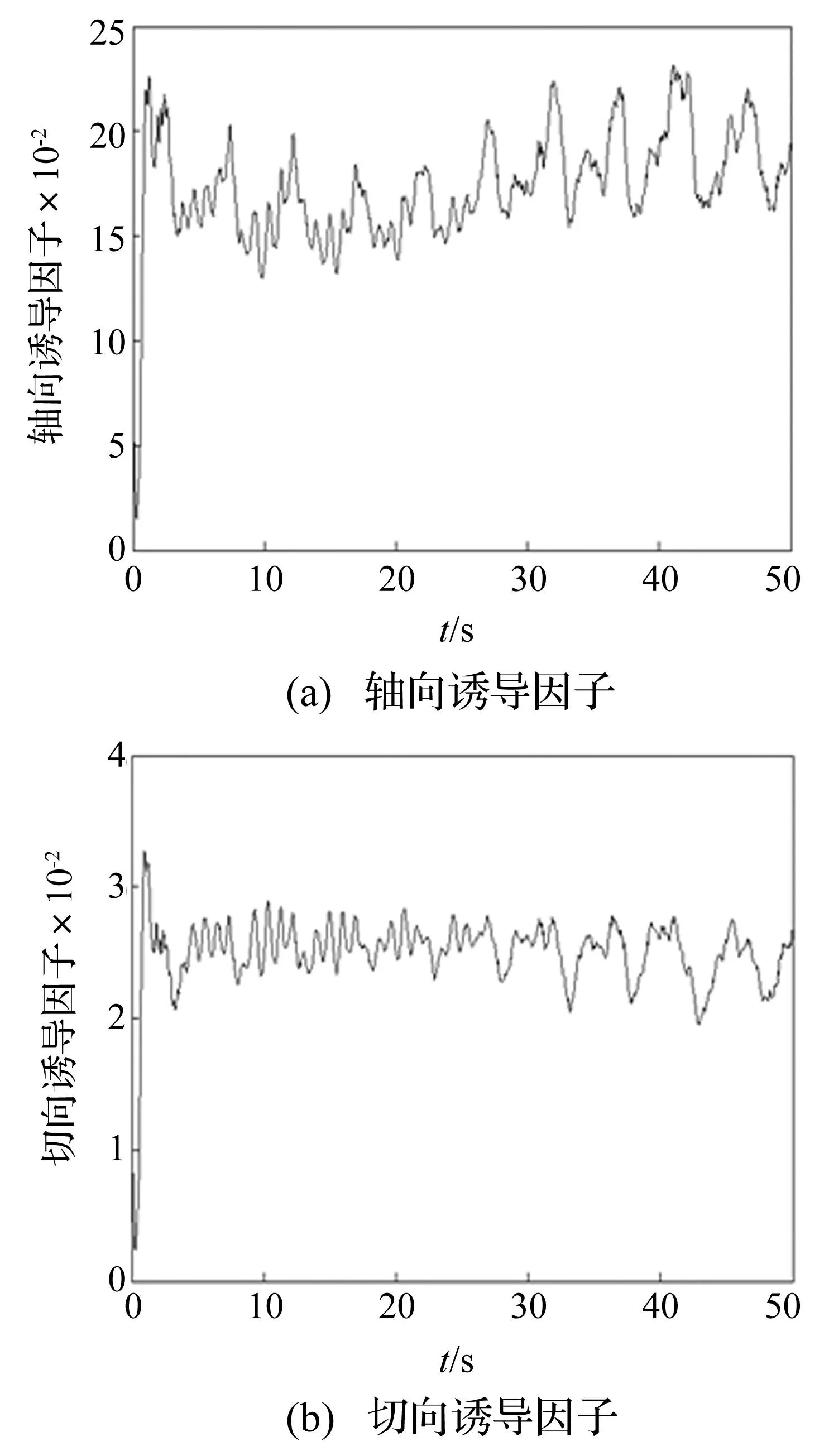
图8　叶尖轴向和切向诱导因子时间历程曲线 Fig.8 The time history curves of axial and tangential inducing factors at the blade tip

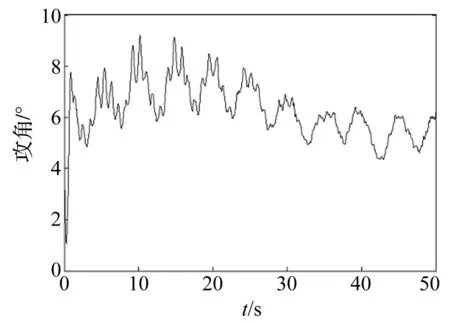
图9　刚体B 13(叶尖)质心截面上攻角的时间历程曲线 Fig.9 The time history curve of attack angle in the center-mass section of rigid body B 13 (blade tip )

图8(a)和(b)分别为叶尖轴向诱导因子和切向诱导因子随时间的变化情况。图8(a)中轴向诱导因子在0.15～0.25左右变化，小于0.4；图8(b)中切向诱导因子较小，仅在0.025左右变化。说明在风力机运行过程中，尾流较稳定，其旋转速度较小。

叶尖是叶片变形最大的位置，需要了解其气动参数随时间的变化情况。图9为刚体B13(叶尖)质心截面上的攻角的时间历程曲线。由于叶片的各种振动的叠加作用，导致叶尖攻角产生波动，但大约保持在5°～9°范围内。

图10(a)和(b)分别为叶片各刚体在叶片坐标系X′方向(挥舞)和Z′方向(摆振)的位移。刚体B1(叶根)代表叶片上与轮毂固结的刚体，其运动被约束，故X′方向和Z′方向位移均为零，距离风轮主轴越则位移越大。从图10(a)中可以看出叶片在X′方向由于持续受到气动推力作用而产生变形，叶尖处变形最大，约为5 m左右。当风力机进入到稳定运行阶段后，由于攻角的变化，引起气动载荷的改变，导致叶片出现挥舞振动。图10(b)中叶片在摆振方向受到了由气动载荷在风轮旋转平面内产生的切向力的作用，故叶片在旋转平面内的振动较为频繁。

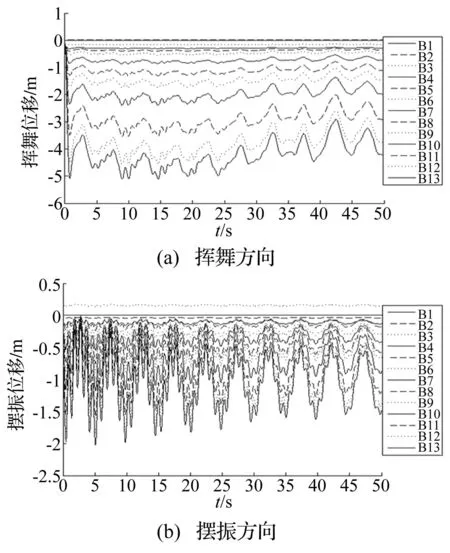
图10 各刚体挥舞与摆振位移(叶片坐标系) Fig.10 The flapwise and edgewise displacement of each rigid body (in blade coordinate system)

6结论

(1)本文针对大型风力机柔性叶片的气弹耦合进行研究。由于叶片动力学微分方程的非线性与耦合的复杂性，文中应用超级单元法将柔性叶片离散为有限个刚体组成的多体系统，用较少的自由度来模拟这种耦合。应用计算多体动力学理论，建立柔性叶片多体系统的非线性代数-微分气弹耦合方程，结合适当的数值求解方法，实现了柔性叶片的非线性气弹耦合时域响应分析。算例对5 MW的风力机在紊流风速下的非线性气弹响应进行了数值模拟。

(2)通过MATLAB仿真平台，编制了柔性叶片气弹耦合模型的构建与数值求解的程序，使得叶片多刚体模型的构建与求解的程序化，在叶片设计或优化阶段，仅需调整输入参数，就能得到不同的优化结果。对于变速或定转速风力机，通过建立相应的转速约束条件，可以实现相应的运动分析。除叶片的运动分析外，增加内力分析模块，可以分析叶片危险截面内力和变形，实现在特殊风况条件下叶片的强度、刚度校核。在叶片适当位置施加脉冲激励，通过传递函数分析，可以得出叶片的根迹图，以及叶片动力特性如固有频率、振型、气弹阻尼等与气弹稳定性相关的分析。在输入文件中，通过增加或减少超级单元的个数，可对分析精度或计算量进行调整。

(3)算例分析表明，长大叶片在随机风载荷作用下，其挥舞与摆振等均为大幅值的非线性振动，且随着风力机单机的功率不断增大、叶片的柔性不断增加，叶片的振动对叶片的气动力有强烈的反馈，二者间相互影响即气弹耦合越加明显。

(4)大型风力机柔性叶片在紊流作用下的气弹耦合时域响应分析，不仅在风力机叶片的设计阶段，同时在风力机运行过程中，为保证其安全稳定运行均有重要的应用价值，也是进行叶片气弹稳定性分析的重要基础。本文的工作为进一步研究柔性叶片非线性气弹失稳机理与气弹失稳影响因素，构建整机的气弹耦合分析模型提供有参考价值的思路和平台。

参考文献

[1]Hansen M O L, SØrensen J N, Voutsinas S, et al. State of the art in wind turbine aerodynamics and aeroelasticity[J]. Progress in Aerospace Sciences,2006, 42: 285-330.

[2]Molenaar D P. Modeling and control of the NedFlex turbine-NedFlex: a flexible, variable rotational speed wind turbine[R]. Mechanical Engineering, Systems and Control Group, Delft University of Technology, The Netherlands, Technical Report TUD-WBMR-A-746,August,1996.

[3]Molenaar D P. Modeling the structural dynamics of the Lagerwey LW-50/750 turbine. Wind Engineering,1998,22(6):253-264.

[4]Molenaar D P. Cost-effective design and operation of variable speed wind turbines[D]. Ph.D. Thesis: Delft University of Technology,2003.

[5]Rauh J, Schiehlen W. Various approaches for the modeling of flexible robot arms[C]// Proceedings of the Euromech-Colloquium 219 on Refined Dynamical Theories of Beams, Plates, and Shells and their Applications, Kassel, 1986, Springer-Verlag, Berlin Heidelberg,1987:420-429.

[6]Zhao X Y, Peter M, Wu J Y. A new multibody modelling methodology for wind turbine structures using a cardanic joint beam element. Renewable Energy,2007, 32:532-546.

[7]Holierhoek J G. Aeroelasticity of large wind turbines[D]. Ph.D. Thesis: Delft University of Technology,2008.

[8]Meng F Z.Aero-elastic stability analysis for large-scale wind turbines[D]. Ph.D. Thesis:Delft University of Technology,2011.

[9]Hansen M O L. Aerodynamics of wind turbines(2nd ed)[M].UK: Earthscan,2008.

[10]Kim S, Sclavounos P D. Fully coupled response simulations of theme offshore structure in water depths of up to 10 000 feet[C]. In: Proceedings of 11th International Offshore and Polar Engineering Conference (ISOPE), Stavanger, Norway, 2005: 457-466.

[11]任勇生,林学海.风力机叶片挥舞/摆振的动力失速非线性气弹稳定性研究[J].振动与冲击,2010,29(1): 121-124.

REN Yong-sheng, LING Xue-hai. Flap/lead-lag nonlinear aeroelastic stability of a wind turbine blade system during dynamic stall[J]. Journal of Vibration and Shock,2010,29(1): 121-124.

[12]任勇生,刘廷瑞.具有结构阻尼的复合材料薄壁梁的动力失速非线性颤振特性[J].振动与冲击,2013, 32(18): 146-152.

REN Yong-sheng, LIU Ting-rui. Stall nonlinear flutter behavior of a thin-walled composite beam with structural damping[J]. Journal of Vibration and Shock,2013, 32(18): 146-152.

[13]任勇生,刘廷瑞,杨树莲,等.风力机复合材料叶片的动力失速气弹稳定性研究[J].机械工程学报,2011, 47(12): 113-125.

PEN Yong-sheng, LIU Ting-rui, YANG Shu-lian. Aeroelastic Stability Analysis of Composite Wind Turbine Blade Dynamic Stall[J]. Journal of vibration engineering,2011, 47(12): 113-125.

[14]刘廷瑞,任勇生.基于复合材料薄壁结构的转子叶片非线性气弹时域响应分析[J].太阳能学报,2012,33(1): 105-112.

LIU Ting-rui, REN Yong-sheng. Nonlinear aeroelastic response analysis of rotor blade modeled as composite thin-walled structure [J].Acta Energiae Solaris Sinica,2012,33(1):105-112.

[15]Li L, Li Y H, Liu Q K, et al. Flapwise non-linear dynamics of wind turbine blades with both external and internal resonances[C]. International Journal of Non-Linear Mechanics, 2014.

[16]Masarati P. Comprehensive multibody aero servo elastic analysis of inte-grated rotorcraft active controls[C]. Ph D thesis, Politecnio di Milano, Di-partimento di Ingegneria Aerospaziale, Jul,2000.

[17]Laino D J,Hansen A C. User’s guide to the wind turbine aerodynamics computer software. Technical report, Windward Engineering[D]. LC, Salt Lake City, UT 84117, December,2002.

[18]Ahlström A. Aeroelastic simulation of wind turbine dynamics[D]. Ph.D. Thesis: Royal Institute of Technology; 2005.

[19]Jonkman J, Butterficle S, Msuial W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. Springfield: U.S.National Rene-wable Energy Laboratory, 2009.

[20]洪嘉振.计算多体系统动力学[M]. 北京：高等教育出版社，1999.

[21]李春，叶舟，高伟,等.现代陆海风力机计算与仿真[M]. 上海：上海科学技术出版社，2012.

[22]袁波,应惠清,徐佳炜.基于线性滤波法的脉动风速模拟及其MATLAB程序的实现[J].结构工程师，2007,23(4):55-61.

YUAN Bo, YING Hui-qing, XU Jia-wei. Simulation of turbulent wind velocity based on linear filter method and MATLAB program realization [J].Structural Engineers, 2007, 23(4):55-61.