梁式桥抗震设计的弹塑性位移反应谱
第一作者李宇男,博士后,副教授,硕士生导师,1982年生
梁式桥抗震设计的弹塑性位移反应谱
李宇,王森,车艳阳,武芳文(长安大学公路学院旧桥检测与加固技术交通行业重点试验室, 西安710064)
摘要:合理选取四类场地320条强震记录,研究地震动特性及恢复力模型动力参数对弹塑性位移谱与残余位移谱影响。结果表明,给出某一标准设防烈度的弹塑性反应谱,其它设防烈度下弹塑性反应谱可据PGA设防烈度与PGA标准烈度比值调整获得;可忽略屈服后刚度比对弹塑性位移谱影响,但应选择偏于保守的屈服后刚度比统计残余位移谱,由此建立的残余位移谱只适用短周期、低延性一般规则桥梁中、低矮桥墩的抗震设计;阻尼比与位移延性比为影响弹塑性位移谱及残余位移谱重要因素,阻尼比增大会减少桥梁非弹性变形及震后残余位移。基于该结果建立适用于我国梁式桥抗震设计的弹塑性及残余位移谱,为考虑残余位移影响的梁式桥基于性能的抗震设计提供重要参考依据。
关键词:弹塑性反应谱;抗震设计;地震动峰值加速度;屈服后刚度;延性
基金项目:国家自然科学基金资助项目(51408042,51408040);陕西省自然科学基金资助项目(2014JQ7253);中央高校基本科研业务费专项资金资助(2013G1211006)
收稿日期:2013-12-05修改稿收到日期:2014-04-10
中图分类号:U442.5文献标志码:A
Elasto-plastic response spectra for beam bridge’s aseismic design
LIYu,WANGSen,CHEYan-yang,WUFang-wen(Key Laboratory of Ministry of Communications for Bridge Detection & Reinforcement Technology, School of Highway, Chang’an University, Xi’an 710064, China)
Abstract:With 320 strong ground motion records of four sites appropriately selected, the elasto-plastic dynamic analysis was performed to study the effects of characteristics of earthquake motions and dynamic parameters of a restoring force model on elasto-plastic displacement spectra and residual displacement spectra. The study results showed that elasto-plastic response spectra of other protected earthquake intensity can be obtained by adjusting elasto-plastic response spectra of a standard protected earthquake intensity according to the ratio of PGA for protected earthquake intensity to PGA for standard protected earthquake; effects of yielding rigidity ratio on elasto-plastic displacement spectra can be neglected, but conservative yielding rigidity ratio is chosen to establish residual displacement spectra which can be applied in low and medium-height piers’ aseismic design of general regular bridges with short natural periods and low ductility; elasto-plastic displacement spectra and residual displacement spectra are affected obviously by both damping ratio and ductility, elasto-plastic displacements and residual displacements of bridge decrease with increase in damping ratio. Based on the above results, the elasto-plastic displacement spectra and residual displacement spectra applicable to aseismic design for Chinese bridges were established. They provided an important guidance for performance-based aseismic design of beam bridges considering the effects of residual displacements.
Key words:elasto-plastic response spectra; aseismic design; peak ground motion acceleration (PGA); yielding rigidity; ductility
非线性静力分析法(NSP)[1, 14-20]为计算结构弹塑性地震响应方法之一。由于NSP法需弹塑性反应谱为其提供目标位移及弹塑性需求谱,故针对弹塑性反应谱的研究已广泛开展。Newmark等[2]将10条常用地震动记录作为输入,给出几种不同的非线性反应谱。陈聃等[3]建立以延性系数为谱坐标、能反映地震动对结构强度及延性两方面要求的非线性反应谱。韦承基等[4]建立弹塑性位移比谱,并考虑不同结构强度影响。程民宪等[5]研究结构低周疲劳性能对地震破坏反应影响,并给出以残余强度为谱坐标的非线性反应谱。Lieping等[6]给出体系最大总输入能增量与最大弹塑性位移关系式。Fajfar等[7-8]采用力降低系数、性能系数或延性折减系数对弹性反应谱进行折减,直接获得弹塑性反应谱。
关于弹塑性反应谱研究虽有许多成果,但所依据的地震动记录太少不具统计规律,或仅由经验公式推导,结果过于粗略,离工程设计应用尚远。因此,本文选取四类场地的320条强震记录,采用与钢筋混凝土受弯构件试验吻合较好的Takeda双线性刚度退化模型,利用SDOF弹塑性动力分析程序,研究地震动特性及恢复力模型动力参数对弹塑性、残余位移谱影响,建立适用于我国桥梁结构抗震设计的弹塑性、残余位移谱。
1基本理论
弹塑性反应谱为考虑结构非线性变形的地震反应谱。该反应谱除受结构周期、阻尼特性影响外,与结构响应的弹塑性程度有关,可定义为具有一定阻尼的SDOF弹塑性体系对实际地面运动最大反应与体系自振周期的关系曲线。对某SDOF体系,可据其自振周期及阻尼在弹塑性反应谱中求得体系弹塑性地震响应的最大值。
质量为m的弹塑性单自由度体系在强地面运动作用下的运动微分方程[9]为
(1)
式中:r(x)为弹塑性SDOF体系恢复力。
结构处于弹性阶段时,r(x)仅为时间的函数;而结构进入非弹性变形阶段后r(x)则随结构位移的改变而改变。在结构动力参数中引入适当塑性影响参数后即可获得各种形式的弹塑性反应谱,包括弹塑性加速度谱Sat、弹塑性位移谱Sd、残余位移谱Dres等。
2地震波选取
以文献[10-11]为依据,从PEER[12]强震记录数据库中挑选主要地震事件(断层距在6.2~161.7 km、震级5.7~7.6)320条强震记录(Ⅰ、Ⅱ、Ⅲ、Ⅳ类场地各80条),其震级、震中距分布情况见图1。
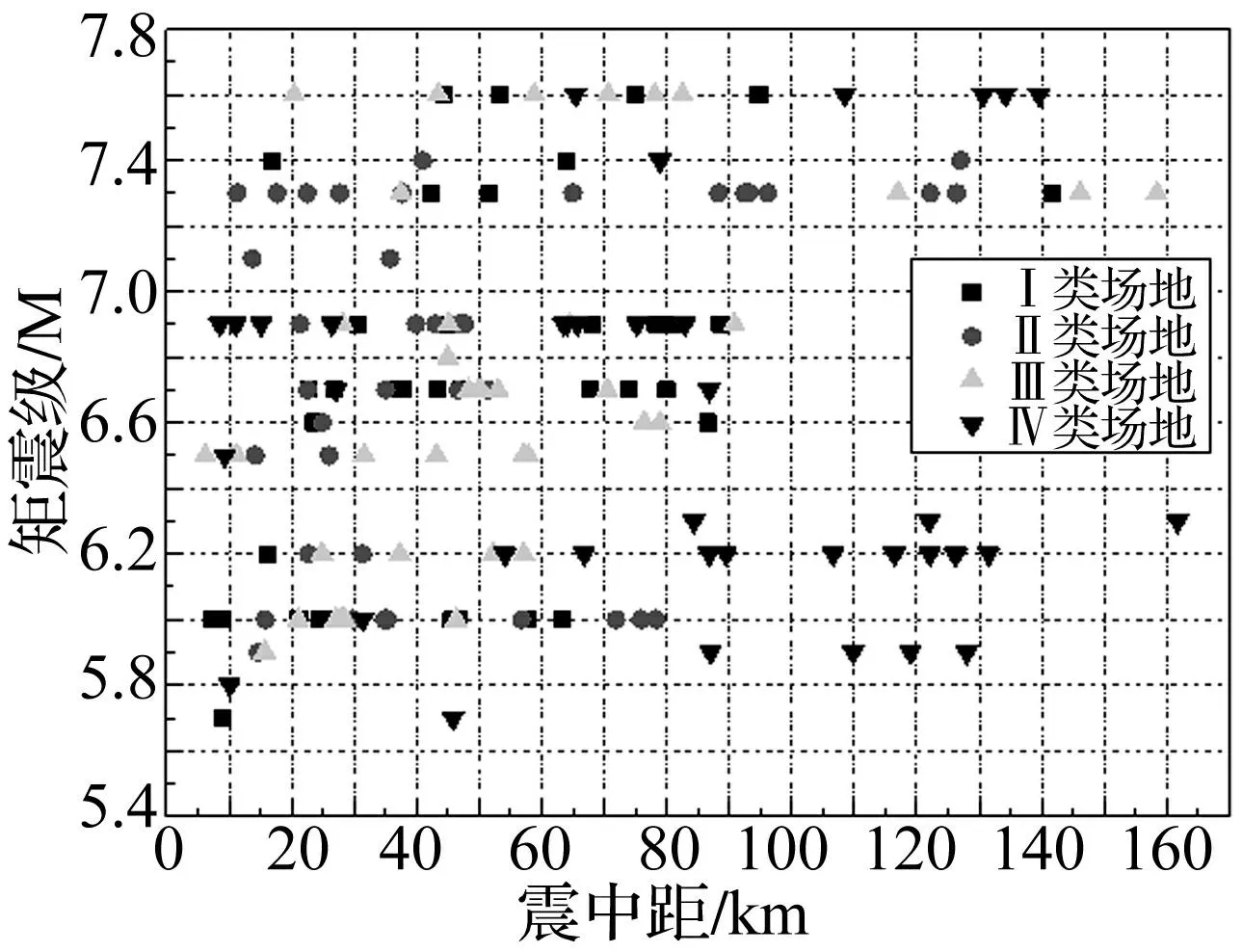
图1 震级-距离分布 Fig.1 Magnitude-distance distribution
图2为以320条地震波为激励统计所得四类场地动力放大系数β曲线(ξ=5%),并与文献[10]进行比较。可以看出,本文统计的β曲线总体上与规范值符合较好,说明所选320条地震动记录特性基本符合规范要求。
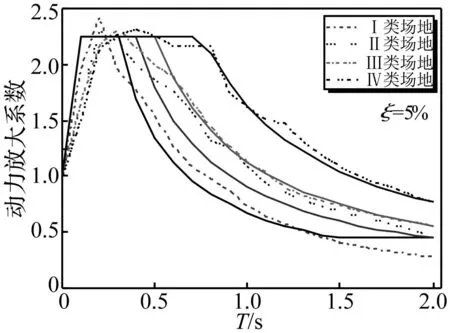
图2 不同场地动力放大系数 Fig.2 Dynamic magnification factors in different sites
3弹塑性反应谱参数影响研究
3.1地震动峰值加速度影响
以I类场地为例,采用Takeda双线性刚度退化模型,阻尼比ξ=5%,屈服后刚度比η=0.05,位移延性比μ=1.0~5.0。利用Bispec[13]计算罕遇地震下6~9度设防时各类弹塑性反应谱的平均值,研究地震动峰值加速度PGA对弹塑性位移谱Sd及残余位移谱Dres的影响,见图3。由图3看出,其它条件相同时,虽Sd、Dres均随PGA增大而增大,但其谱曲线形状并无太大改变。为找原因,本文以7度Sd谱值为准,6~9度不同周期对应的Sat谱值分别为7度的0.523 1、1.809 8、3.048 1倍,分别与6~9度PGA值与7度PGA值比值大致相同。PGA对Dres影响规律基本相同。因此,只要以某一设防烈度为标准,给出与其相应的弹塑性位移谱、残余位移谱,其它设防烈度下弹塑性位移谱、残余位移谱即可据PGA设防烈度与PGA标准烈度比值调整获得。
3.2屈服后刚度比影响
以I类场地为例,将80条强地震动记录按罕遇地震7度设防标准调幅为0.21 g,采用Takeda双线性刚度退化模型,阻尼比ξ=5%,位移延性比μ=1.0~5.0,利用Bispec[13]分别计算η=0.0, 0.025, 0.05时弹塑性位移谱Sd及残余位移谱Dres的均值。不同η对弹塑性位移谱Sd及残余位移谱Dres的影响见图4。由图4看出,①不同η对应的弹塑性位移谱Sd曲线大体相互重合,故统计Sd谱时可忽略η。②随周期T增加,不同η对应的Dres谱呈递增趋势;随η增大,对应于同一周期的Dres则有所降低。η对短周期(T<1 s)、低延性(μ<3)SDOF体系残余位移Dres影响较小;对中长周期(T>2 s)、大延性(μ>5)SDOF体系的Dres值影响较大。可见,为使桥梁结构的震后残余位移能被限制在容许范围内,应选择偏于保守的η统计残余位移谱Dres,而由此建立的残余位移谱适用于短周期、低延性一般规则桥梁中、低矮桥墩的抗震设计。


图3 PGA对弹塑性反应谱影响Fig.3EffectofPGAontheelasto-plasticresponsespectra图4 刚度比对弹塑性反应谱影响Fig.4Effectofηontheelasto-plasticresponsespectra图5 阻尼比对弹塑性反应谱影响Fig.5Effectofζonelasto-plasticresponsespectra
3.3阻尼比影响
以I类场地为例,将80条地震波按罕遇地震7度设防调幅为0.21 g,采用Takeda双线性刚度退化模型,设屈服后刚度比η=0.05,位移延性比μ=1.0~5.0,结构阻尼比取值分别考虑钢结构(ξ=2%)、钢筋混凝土结构(ξ=5%)及隔震结构(ξ=10%, 14%),利用Bispec[13]分别计算四种阻尼比的弹塑性位移谱Sd及残余位移谱Dres的平均值。
ξ对弹塑性位移谱Sd及残余位移谱Dres影响见图5。由图5看出,随周期T增加不同ξ对应的弹塑性位移谱Sd及残余位移谱Dres均呈递增趋势;而同一周期T对应的弹塑性位移及残余位移值则随ξ增大而减小。原因为地面运动输入结构的能量一定,阻尼比增大造成结构阻尼耗能增加、滞回耗能减少,从而减少结构的非弹性变形及结构震后残余位移。
3.4位移延性比影响
以Ⅲ类场地为例,将80条地震波按罕遇地震7度设防标准调幅为0.21 g,采用Takeda双线性刚度退化模型,阻尼比ξ=5%,屈服后刚度比η=0.05,用Bispec[13]计算μ=1.0~5.0时各类弹塑性反应谱的平均值,研究μ变化对弹塑性位移谱Sd及残余位移谱Dres影响,见图6。由图6看出,①随μ增大弹塑性位移谱Sd总体呈递减趋势,尤其μ>3后,不同μ对应的Sd谱曲线趋于一致;对中短周期结构而言,可忽略μ对Sd谱影响。②Dres谱值均随μ的增大而增大;当μ>3后,不同μ对应的Dres谱曲线亦将趋于一致。
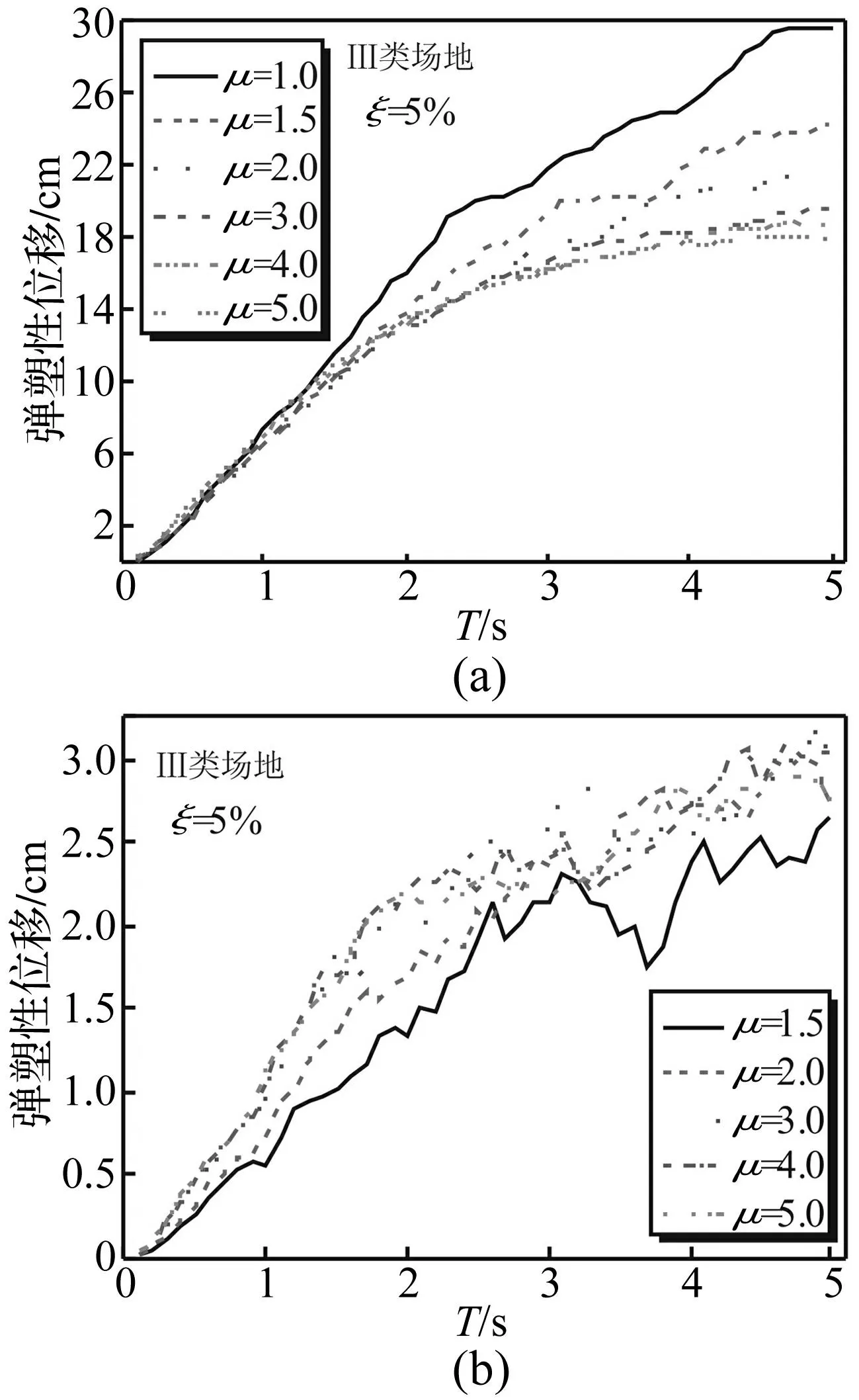
图6 位移延性比对弹塑性反应谱影响 Fig.6 Effect of ductility on elasto-plastic response spectra
4弹塑性反应谱建立
将320条强震记录作为地震动输入,采用Takeda双线性刚度退化模型,利用Bispec[13]计算周期在0.05~5 s、位移延性比μ=1.0~6.0及阻尼比ξ=1%~15%的弹塑性位移谱Sd及残余位移谱Dres的平均值,获得具有统计意义的弹塑性位移谱及残余位移谱,进而为考虑残余位移影响的桥梁基于性能抗震设计方法提供设计谱。限于篇幅,仅给出ξ=5%、μ=1.0~6.0、罕遇地震7度设防时,四类场地的弹塑性位移谱Sd及残余位移谱Dres,其它设防烈度的Sd、Dres谱可由PGA设防烈度与PGA7度罕遇的比值调整获得。
4.1弹塑性位移谱
统计所得弹塑性位移谱见图7。由图7看出,①各场地的弹塑性位移谱曲线均随周期T的增加呈递增趋势;②随场地土质变软,弹塑性位移谱值呈递增趋势,较其它三类场地,Ⅳ类场地的弹塑性位移谱值最大。

图7 四类场地弹塑性位移谱 Fig.7 Elasto-plastic displacement spectra in four sites

图8 不同场地条件下残余位移谱 Fig.8 Residual displacement spectra in different site
4.2残余位移谱
统计所得残余位移谱见图8。由图8看出,①各场地残余位移谱均随T的增加而增大;②随μ增大各场地残余位移谱值随之增大;③场地条件对残余位移谱影响较大,其它条件相同时,Ⅱ类场地残余位移谱值最小,而其它三类场地残余位移谱值则随场地土质变软而增大。
5结论
本文通过合理选取强震记录,研究地震动特性、恢复力模型动力参数对弹塑性位移谱及残余位移谱影响,建立适用于我国桥梁抗震设计的弹塑性位移谱及残余位移谱,结论如下:
(1)给出某一设防烈度的弹塑性位移谱、残余位移谱,其它设防烈度下弹塑性、残余位移谱可据PGA设防烈度与PGA标准烈度的比值调整获得。
(2)可忽略屈服后刚度比对弹塑性位移谱影响,应选择偏于保守的屈服后刚度比统计残余位移谱。由此建立的残余位移谱适用于短周期(T<1 s)、低延性(μ<3)一般规则桥梁中、低矮桥墩的抗震设计。
(3)阻尼比及位移延性比为影响弹塑性位移谱及残余位移谱重要因素,而阻尼比增大会减少桥梁结构的非弹性变形及震后残余位移。
(4)弹塑性反应与多种非线性因素有关,若需获得可靠的反应谱,需进行大量验证,尤其对弹塑性地震反应分析结果的验证[21]。本文所建弹塑性位移谱及残余位移谱可为桥梁基于性能的抗震设计提供重要参考依据。
参考文献
[1]何文福, 刘文光,杨骁,等. 隔震结构弹塑性反应谱分析研究[J]. 振动与冲击, 2010, 29(1): 30-33.
HE Wen-fu, LIU Wen-guang,YANG Xiao,et al. Elasto-elastic response spectra of isolated[J]. Journal of Vibration and Shock, 2010, 29(1): 30-33.
[2]Newmark N M, Hall W J. Seismic design criteria for nuclear reactor facilities[C].//Proceedings of the 4th World Conference on Earthquake Engineering Santiago, Chile, 1969: 37-50.
[3]Chen Dan. Ductility spectra and collapse spectra for earthquake resistant structures[C].//Proc.7th European Conference on Earthquake Engineering, 1982.
[4]韦承基. 弹塑性结构的位移比谱[J]. 建筑结构学报, 1983, 4(2): 40-48.
WEI Cheng-ji. Displacement ratio spectrum of elastoplastic structures[J].Journal of Building Structures, 1983, 4(2): 40-48.
[5]Cheng Ming-xian. Residual strength spectra for earthquake resistant structures[C].//Proc.1st Conference on Design, Construction and Repair of Building Structures in Earthquake Zones, 1987.
[6]Ye L P,Maximum O S. Seismic displacement of inelastic systems based on energy concept[J]. Earthquake Engineering and Strucutral Dynamics, 1999,28:1483-1499.
[7]Fajfar P, Fischinger M. Earthquake design spectra considering duration of ground motion[C].//Proc.4th U.S.NCEE, California, 1990:15-24.
[8]Tolis S V, Faccioli E. Displacement design spectra[J]. Journal of Earthquake Engineering,1999,3(1):107-125.
[9]王博,白国良,代慧娟.典型地震动作用下长周期单自由度体系地震反应分析[J].振动与冲击,2013, 32(15): 190-196.
WANG Bo,BAI Guo-liang,DAI Hui-juan.Seismic response analysis of long-period SDOF system under typical ground motions[J].Journal of Vibration and Shock,2013,32(15):190-196.
[10]GB50111-2006,铁路工程抗震设计规范[S].
[11]JTG/TB02-01-2008,公路桥梁抗震设计细则[S].
[12]弓俊青,朱晞. 以位移为基础的钢筋混凝土桥梁墩柱抗震设计方法[J].中国公路学报,2001,14(4): 42-46.
GONG Jun-qing, ZHU Xi. Displacement}ased seismic design method for RC bridge columns[J]. China lournal of Highwav and Transport, 2001, 14(4): 42-46.
[13]黄建文,朱晞. 近场地震作用下钢筋混凝土桥墩基于位移的抗震设计[J].土木工程学报,2005, 38(4): 84-90.
HUANG Jian-wen ZHU Xi. Displacement based seismic design for rc bridge columns under near fault earthquakes[J]. China Civil Engineering Journal, 2005, 38(4): 84-90.
[14]Kawashima K, MacRae G A, Hoshikuma J, et al. Residual displacement response spectrum[J]. Journal of Structural Engineering, 1998, 124(5): 523-530.
[15]Kawashima K. Seismic design and retrofit of bridges[C]. 12WCEE, New Zealand, Reference No.2828, 2000.
[16]Japanroad association. design specifications of highway bridges, part V: seismic design[S]. Tokyo, Japan, 1996.
[17]Riddell R,Newmark N M. Statistical analysis of the response of nonlinear systems subjected to earthquakes[R]. University of Illinois, Urban, Illinois, 1979.
[18]Mahin S A, Bertero V V. An evaluation of inelastic seismic response spectra[J]. Journal of the Structural Division, 1981, 107(ST9): 1777-1795.
[19]MacRae G A, Kawashima K. Post-earthquake residual displacements of bilinear oscillators[J]. Earthquake Engineering and Structural Dynamics, 1997,26(77): 701-716.
[20]Zatar W A, Mutsuyoshi H. Reduced residual displacements of partially prestressed concrete bridge piers[C]. 12WCEE, New Zealand, Reference No.2828, 2000.
[21]李宇. 考虑残余位移和土-结构相互作用的桥梁结构基于性能的抗震设计及评估[D]. 北京:北京交通大学, 2010.


