低噪音深沟球轴承振动特性研究
第一作者邓四二男,博士,教授,博士生导师,1963年生
低噪音深沟球轴承振动特性研究
邓四二1,孙朝阳2,顾金芳3,崔永存1(1.河南科技大学机电工程学院,河南洛阳471003; 2.洛阳轴研科技股份有限公司,河南洛阳471039;3.上海天安轴承有限公司,上海201108)
摘要:在滚动轴承动力学分析理论基础上建立含轴承零件工作表面波纹度的深沟球轴承动力学数学模型,并以某型号低噪音深沟球轴承为例,对不同结构参数、工况参数及谐波参数下低噪音深沟球轴承的振动特性进行理论分析。结果表明,合理选取径向游隙、内外沟曲率半径系数及保持架兜孔间隙等参数能使轴承本身达到减振降噪目的;振动值随轴承宽度增加逐渐减小;施加一定轴向载荷能有效降低轴承振动;存在的合理转速使用范围能有效降低轴承振动;内外滚道谐波阶次等于钢球数目整数倍时,轴承振动明显加剧;外滚道激励谐波对应的激励频率为kzfc,内滚道激励谐波对应的激励频率为kzfc+fs;偶次谐波阶次钢球表面波纹度对轴承振动有激励作用;轴承旋转套圈会激励更大的轴承振动值;瞬时载荷增加或瞬时速度提高均会致轴承振动增大。
关键词:深沟球轴承;低噪音;表面波纹度;振动
基金项目:国家十二五科技攻关项目(JPPT-ZCGX1-1);河南省科技创新杰出人才(144200510020)
收稿日期:2014-01-28修改稿收到日期:2014-04-16
中图分类号:TH113文献标志码:A
Vibration characteristics of low-noise deep groove ball bearings
DENGSi-er1,SUNChao-yang2,GUJin-fang3,CUIYong-cun1(1. School of Mechatronic Engineering, Henan University of Science and Technology, Luoyang 471003, China; 2. Luoyang Bearing Science and Technology Co., LTD, Luoyang 471039, China; 3. Shanghai Tianan Bearing Co., LTD, Shanghai 201108, China)
Abstract:Based on the dynamic analysis theory of rolling bearings, a dynamic model for deep groove ball bearings considering the effects of bearing components’ working surface waviness was established. Taking a type of low-noise deep groove ball bearing as an example, the bearing vibration characteristics were analyzed theoretically with various bearing structural parameters, working conditions and working surface wavinesses. The results showed that the bearing basic vibration can be reduced by selecting reasonable primary parameters, for instance, bearing radial clearance, inner and outer raceway groove curvature radius coefficients, pocket clearance of cage, and so on; the larger the bearing width, the smaller the bearing vibration; a certain axial loads can reduce effectively the bearing vibration; there is a reasonable rotating speed range for smaller bearing vibration; the severe vibration occurs when the inner and outer raceway surface waviness orders are an integer multiple of the number of balls; the exciting frequency corresponding the waviness orders of outer raceway is kzfc and that of the inner raceway is kzfc+fs; the even waviness orders of ball working surface has an exciting effect on the bearing vibration; the vibration produced by rotating ring is more severe than that of fixed ring; the bearing vibration increases greatly with increase in radial loads or rotating speed.
Key words:deep groove ball bearing; low-noise; surface waviness; vibration
航空发动机所用深沟球轴承除长寿命要求外,振动、噪声要求亦较高。噪声由轴承运转过程中产生振动以声波形式经周围介质(如空气)传播所致,故振动为轴承噪声根源。轴承振动涉及其结构参数、工况条件、润滑剂及工艺误差等诸多因素,产生机理非常复杂。目前有关滚动轴承振动研究大多基于轴承加工工艺参数引起的振动激励机理[1-5]。夏新涛等[6]通过研究轴承工作表面谐波分布与轴承振动关系,提出控制轴承套圈加工谐波参数以达到降低振动;邓四二等[7]提出轴承套圈光饰强化方法,通过减小轴承套圈滚道波纹度幅值实现减振降噪目的;Wardle等[8-9]从理论、试验两方面研究并验证滚道表面波纹度是产生轴承振动激振力根源;Aktürk[10]对轴承内、外滚道接触表面及钢球接触表面波纹度阶次与轴承振动频率关系进行研究。所有研究均基于轴承加工参数波纹度量与振动量的关系分析,缺乏对低噪音轴承结构参数对振动影响系统研究。鉴于此,本文在深沟球轴承动力学分析基础上,建立含轴承零件接触面加工波纹度的深沟球轴承动力学数学模型,理论研究低噪音深沟球轴承振动特性,并对低噪音深沟球轴承结构参数与振动关系进行分析。可为低噪音深沟球轴承结构参数选取及加工工艺参数控制提供理论依据。
1低噪音深沟球轴承动力学数学模型
1.1轴承接触表面波纹度数学模型

图1 内外滚道波纹度模型 Fig.1 Waviness model of inner and outer raceway
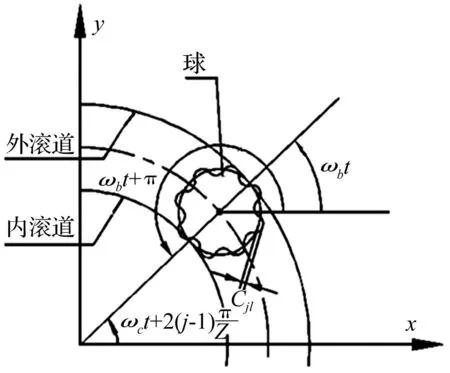
图2 钢球波纹度模型 Fig.2 Waviness model of ball
深沟球轴承内、外滚道与钢球接触处表面形貌及保持架工作面形貌直接影响内、外滚道与钢球间相互作用力,从而影响其振动特性。轴承内、外套圈及保持架工作表面存在非常复杂的三维形貌,需扫描获得三维实体形貌图后据其进行数学建模,过程较复杂。为研究方便,本文对轴承工作表面形貌简化处理,主要考虑内、外滚道及钢球工作表面,略去保持架工作表面形貌,对内、外滚道仅考虑钢球与滚道接触点法向平面内波纹度,见图1。钢球为球体,在任一截面上钢球波纹度设为一致,见图2。
钢球与内、外沟道接触处各零件接触表面波纹度可用余弦函数表示[11-12]。
外圈滚道接触处表面波纹度为
2πl(j-1)/Z+α1l]
(1)
内圈滚道接触处表面波纹度为
2πl(j-1)/Z+α2l]
(2)
钢球与外滚道接触处钢球表面波纹度为
(3)
钢球与内滚道接触处钢球表面波纹度为
(4)
式中:l为表面谐波数;q为总谐波数;A1l,A2l分别为某l次谐波对应的外、内圈滚道表面波纹度幅值,单位μm;Cjl为第j个钢球某l次谐波对应的钢球表面波纹度幅值,单位μm;ω1,ω2,ωc,ωb为轴承外内圈、保持架及钢球自转角速度,对应转速分别为n1,n2,nc,nb,关系分别为ω1=2πn1,ω2=2πn2,ωc=2πnc,ωb=2πnb;α1l,α2l分别为某l次谐波对应的外、内圈滚道表面波纹度函数初始相位角;γjl为第j个钢球某l次谐波对应的钢球表面波纹度函数初始相位角;Z为轴承钢球数。
1.2轴承元件间相互作用力数学模型
深沟球轴承主要承受径向载荷,但使用时一般均在轴向施加一较小预负荷,目的为提高其使用寿命、降低振动,因此深沟球轴承动力学分析可按小接触角角接触球轴承动力学分析方法进行。深沟球轴承钢球受力见图3,保持架受力见图4,钢球与沟道间相互作用后接触角、变形及位移几何关系见图5,相关符号含义见表1,求解见文献[13]。
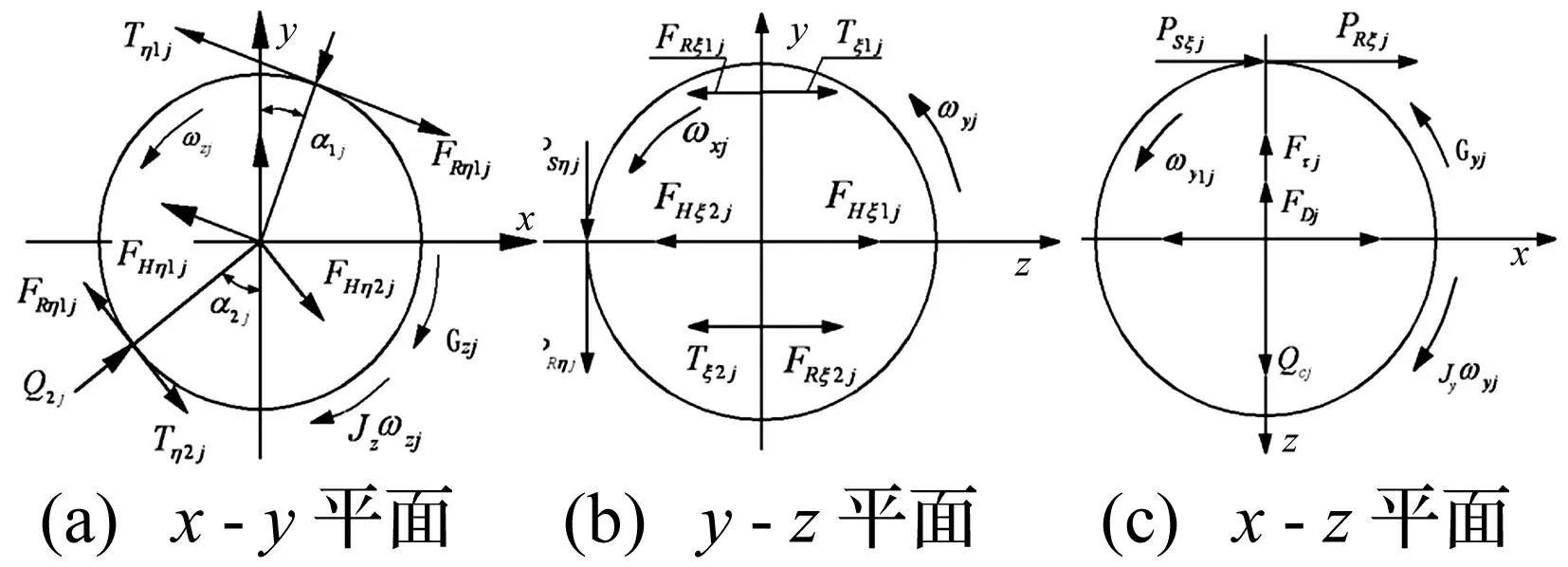
图3 钢球受力示意图 Fig.3 Schematic diagram of ball forces
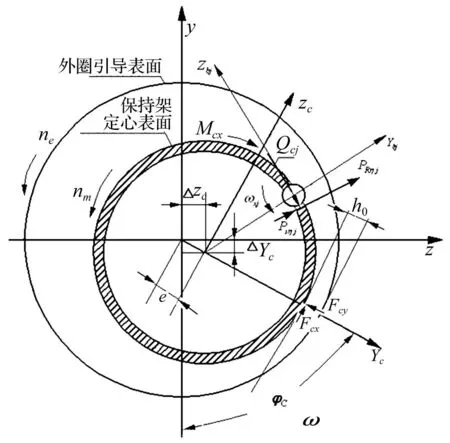
图4 保持架平衡状态 Fig.4 Equilibrium state of cage
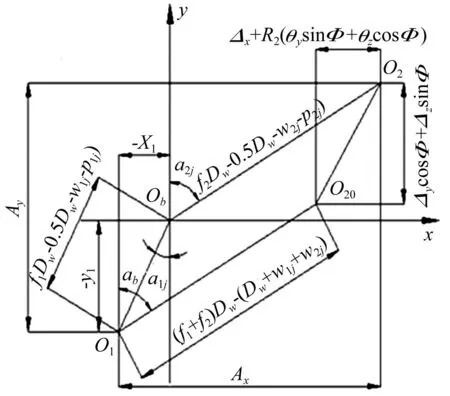
图5 接触角、变形和位移的几何关系 Fig.5 Geometrical relationship of contact angle, distortion and displacement

作用力含义Tη1j钢球-外滚道接触面上的拖动力Tη2j钢球-内滚道接触面上的拖动力FRη1j钢球-外滚道接触入口区的流体动压摩擦力FRη2j钢球-内滚道接触入口区的流体动压摩擦力FHη1j作用于钢球中心的流体动压合力水平分量FHη2j作用于钢球中心的流体动压合力水平分量Q1j钢球与外滚道作用力Q2j钢球与内滚道作用力FNj钢球惯心力分量FDj油-气混合物对钢球的空气动力阻力Tξ1j钢球-滚道接触面上的拖动力Tξ2j钢球-滚道接触面上的拖动力FRξ1j钢球-滚道接触入口区的流体动压摩擦力FRξ2j钢球-滚道接触入口区的流体动压摩擦力FHξ1j作用于钢球中心的流体动压合力水平分量FHξ2j作用于钢球中心的流体动压合力水平分量PRηj作用于兜孔表面流体动压摩擦力PSηj接触面入口区流体动压摩擦力PRξj接触面入口区的流体动压摩擦力PSξj接触面入口区的流体动压摩擦力Qcj法向接触力Fτj钢球惯心力分量ωxj编号为j的钢球X轴角速度分矢量ωyj编号为j的钢球Y轴角速度分矢量ωzj编号为j的钢球Z轴角速度分矢量Jx,Jy,Jz转动惯量X,Y,Z轴分量F'cy作用于保持架的合力Fc的y轴分量F'cz作用于保持架的合力Fc的z轴分量M'cx由体动压油膜的分布压力引起的摩擦力矩Δyc,Δzc保持架质心偏离坐标值α1j,α2j准动力学平衡条件下的工作接触角mb钢球质量x··j,y··j,z··j分别为钢球在x,y,z方向上的加速度
据滚动体、保持架受力情况,建立深沟球轴承动力学微分方程组。
1.2.1滚动体动力学微分方程组
Q2jsinα2j-Q1jsinα1j+Tη2jcosα2j-
Tη1jcosα1j-FRη2jcosα2j+FRη1jcosα1j+
(5)
Q2jcosα2j-Q1jcosα1j-Tη2jsinα2j+Tη1jsinα1j+
FRη2jsinα2j-FRη1jsinα1j-FHη2jsinα2j+
(6)
Tξ1j-Tξ2j-FRξ1j+FRξ2j+FHξ1j-
(7)
0.5(Tξ1j-FRξ1j)DWcosα1j-0.5(PSηj+PRηj)DW+
(8)
0.5(FRξ1j-Tξ1j)DWsinα1j-0.5(PSξj+PRξj)DW+
(9)
0.5(Tη1j-FRη1j)DW+0.5(Tη2j-FRη2j)DW-
(10)
1.2.2保持架动力学微分方程组


(13)
式中:Fcy,Fcz,Mcx为
(14)
式中:
(15)
式(15)中内圈引导为+,外圈引导为-。
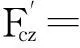
(16)
式(16)中内圈引导为-,外圈引导为+。
1.2.3位移(Δ)-变形(δ1(2)j)相容条件
由图5可得
Ax=[(f1+f2)Dw-(Dw+w1j+w2j)]sinα0+
[Δx+RZ(θysinφ+θzcosφ)]=
[f1Dw-(0.5Dw+w1j)-p1j+δ1j]sinα1j+
[f2Dw-(0.5Dw+w2j)-p2j+δ2j]sinα2j
(18)
Ay=[(f1+f2)Dw-(Dw+w1j+w2j)]cosα0+
[Δycosφ+Δzsinφ]=
[f1Dw-(0.5Dw+w1j)-p1j+δ1j]cosα1j+
[f2Dw-(0.5Dw+w2j)-p2j+δ2j]cosα2j
(19)
式中: α0为轴承原始接触角(输入参数),rad;
(20)
(f2-0.5)Dw-w2j-p2j(m)
(21)
α1j=arctg(x1/y1)(rad)
(22)
α2j=arctg[(Ax-x1)/[Ay-y1]](rad)
(23)
1.2.4轴承内圈动力学微分方程组
(24)
(25)
(26)
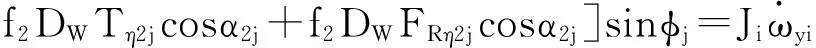
(27)
(28)
式中:
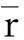
(29)
2深沟球轴承动力学性能分析


表2 轴承结构参数
2.1结构参数对球轴承振动影响
设轴承在环境温度下工作,各零件接触表面为理想真圆,内圈转速10 000 r/min,轴承径向平面内Y轴向径向载荷1 200 N,径向平面内Z轴向径向载荷0 N,轴向载荷(X轴向)0 N。分析结果取轴承内圈质心Y轴向径向振动加速度级描述整个轴承振动水平。
2.1.1径向游隙对轴承振动影响
在0组径向游隙范围内轴承径向游隙值与振动关系见图6。由图6看出,径向游隙对轴承振动影响较大,且呈非线性特性,存在一个使轴承振动最小的合理径向游隙。随径向游隙从5~20μm变化,轴承振动呈先减小后增大趋势,径向游隙为11 μm时轴承振动最小。
2.1.2外沟曲率半径系数对轴承振动影响
径向游隙取11 μm时外沟曲率半径系数与轴承振动关系见图7。由图7看出,随外沟曲率半径系数从0.51变化到0.57,轴承振动呈先减小后增大趋势,f1取值0.530.54时有利于轴承减振降噪。
2.1.3内沟曲率半径系数对轴承振动影响
径向游隙取11 μm时内沟曲率半径系数与轴承振动关系见图8。由图8看出,内沟曲率半径系数选取对轴承振动影响较大。f2>0.52时轴承振动逐渐加剧,本文f2适宜取0.51。
2.1.4宽度对轴承振动影响
轴承宽度与轴承振动关系见图9。由图9看出,随宽度逐渐增大轴承振动越来越小。因此,轴承设计时在其使用空间许可范围内,可通过增大宽度实现轴承减振降噪。
2.1.5保持架兜孔间隙对轴承振动影响
低噪音深沟球轴承保持架类型较多,应用最广的有浪型保持架、尼龙保持架两种,结构见图10。其中,浪型保持架材料为GCr15,尼龙保持架材料为PA66。保持架兜孔间隙对轴承振动影响关系见图11。由图11看出,对两种不同保持架,轴承振动随保持架兜孔间隙增大呈先减小后增大趋势。保持架兜孔间隙取0.1~0.15 mm值时,轴承振动相对较小。从降低轴承振动角度,采用浪型保持架较尼龙保持架好,因尼龙保持架为半开口非对称结构,保持架质心偏离轴承中心截面,相当于为保持架施加一不平衡量,激励轴承产生振动。
对冲压浪型保持架,一般有椭圆形球兜孔与圆形球兜孔两种形状。圆形球兜孔保持架球兜孔半径与深度相等;而椭圆形球兜孔保持架球兜孔半径与深度不相等。本文将保持架球兜孔半径与深度差值定义为保持架球兜孔偏心距,用符号e表示(图10(b))。保持架球兜孔偏心距与轴承振动关系见图12。由图12看出,具有一定球兜孔偏心距的保持架能有效降低轴承振动。随偏心距逐渐增大轴承振动呈先减小后增大趋势。该型号轴承保持架球兜孔偏心距最佳值为0.04 mm。

图6 轴承径向游隙对轴承振动的影响Fig.6Effectofbearingradialclearancesonvibrationvalue图7 外滚道沟曲率半径系数对轴承振动的影响Fig.7Effectofoutergroovecurvatureradiuscoefficientsonvibrationvalue图8 内滚道沟曲率半径系数对轴承振动的影响Fig.8Effectofinnergroovecurvatureradiuscoefficientsonvibrationvalue图9 轴承宽度对轴承寿命的影响Fig.9Effectofbearingwidthonvibrationvalue
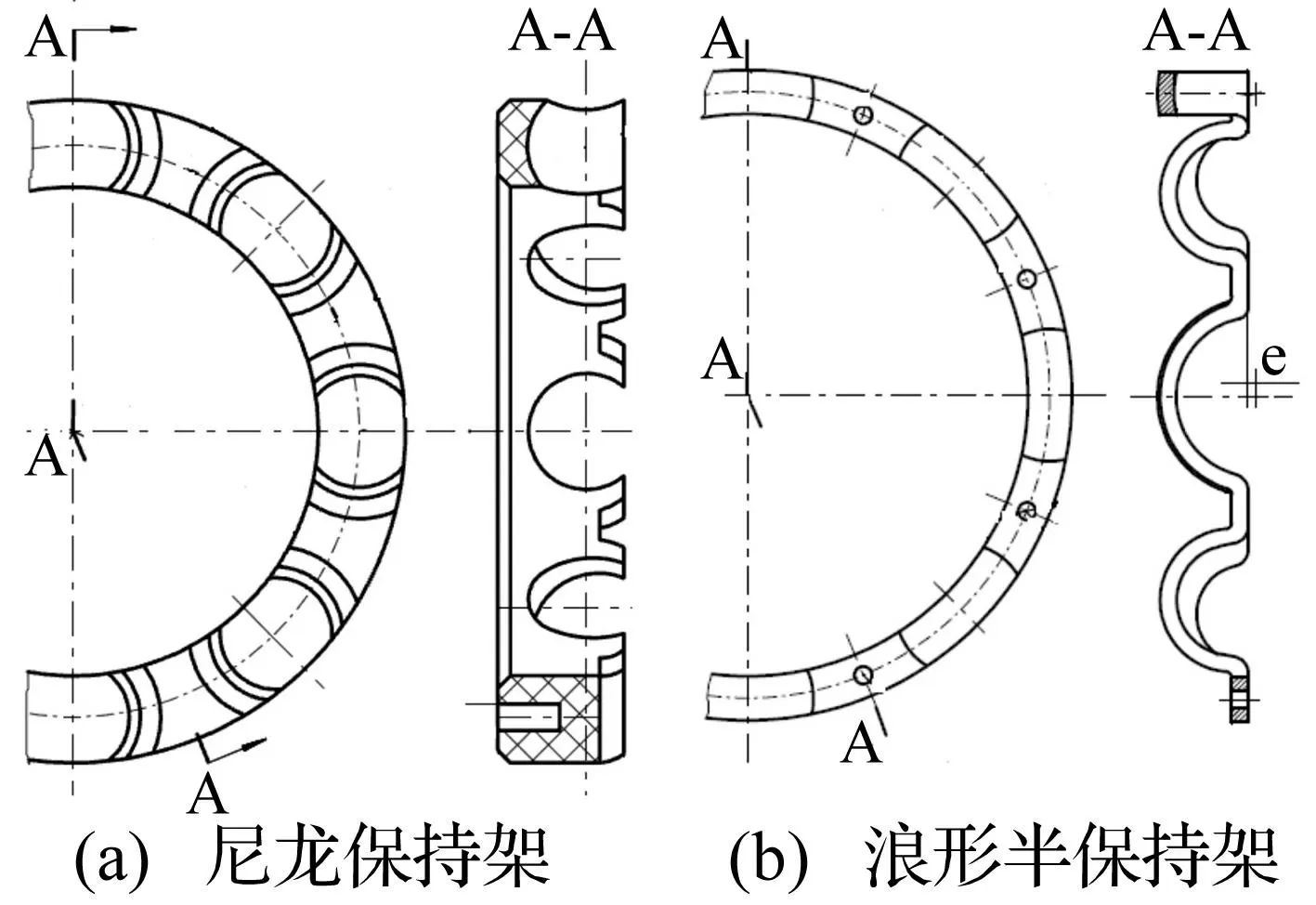
图10 保持架结构图 Fig.10 Diagram of cage structure
2.2工况参数对球轴承振动影响
设轴承内圈旋转、外圈静止,轴承径向游隙取11μm,采用冲压浪型保持架。
2.2.1轴向预载荷对轴承振动影响
在内圈转速n2=11 000 r/min、径向平面内Y轴向轴承径向载荷1 200 N工况下轴向预载荷与轴承振动关系见图13,与轴承寿命关系见图14。由图13看出,对深沟球轴承施加一定轴向预载荷可有效降低轴承振动,且轴向预载荷与轴承额定动负荷之比在0.53%0.89%之间时,轴承振动最小。此分析与文献[14]结论一致。由图14看出,对深沟球轴承施加一定轴向预载荷利于提高轴承疲劳寿命,且轴向预载荷与轴承额定动负荷之比在0.05%0.4%之间时,轴承疲劳寿命最长。综合图13、图14知,对深沟球轴承,轴向预载荷能有效降低轴承振动、提高其疲劳寿命,但较难确定能同时使轴承寿命最大、振动最低的最佳轴向预载荷,低噪音深沟球轴承轴向预载荷选取可在满足使用寿命下使轴承振动最低的合理轴向预载荷。


图11 保持架兜孔间隙对轴承振动的影响Fig.11Effectofthecagepocketclearanceonvibrationvalue图12 保持架球兜孔偏心距对振动的影响Fig.12Effectofthecagepocketeccentricityonvibrationvalue图13 轴承轴向载荷与轴承振动的关系Fig.13Effectofaxialloadsonvibrationvalue图14 轴承轴向载荷与轴承寿命的关系Fig.14Effectofaxialloadsonbearinglife
2.2.2径向载荷对轴承振动影响
内圈转速11 000 r/min、轴向载荷为0 N情况下在径向平面内Y轴向径向载荷与轴承振动关系见图15。由图15看出,随载荷逐渐增大轴承振动越大。
2.2.3转速对轴承振动影响
平面内Y轴径向载荷1 200 N、Z轴径向载荷0 N、轴向载荷0 N工况下轴承转速与振动关系见图16。由图16看出,随转速增大轴承振动呈先增大后减小再增大趋势,转速与振动值之间呈现非线性关系。对低噪音深沟球轴承,存在一个合理的使用转速范围。
2.2.4冲击载荷对轴承振动影响
轴承在使用过程中,会伴随外载荷或转速的瞬时变化。瞬时冲击载荷会激励轴承振动。轴承外载冲击变化量与轴承振动关系见图17。由图17看出,轴承振动随外载冲击量增加而增大。外载冲击变化量与轴承内圈幅频见图18。由图18可知,轴承以593.7 Hz为主要频率,对应的倍频幅值逐渐递减,该主频与理论计算的变刚度频率fvc(fvc=zfc=597.4 Hz)较接近,误差仅0.6%。因此,外载荷变化不会改变轴承振动频率。
轴承转速冲击变化量与振动关系见图19。由图19可知,轴承振动随转速冲击量增大快速增大,轴承振动与转速冲击量之间呈指数关系。轴承转速冲击变化量与振动频率及振幅关系见图20。由图20可知,轴承以648.8 Hz为主要频率,对应的倍频幅值逐渐递减,该主频数值与0.5(fvc1+fvc2)=0.5(597.4+716.8)=657.1较接近,误差仅1.2%。其中fvc1,fvc2为速度变化前后轴承变刚度频率,计算方法同前。
2.3工艺谐波参数对振动影响
设轴承内圈转速10 000 r/min,外圈静止,径向游隙取11 μm,采用冲压浪型保持架;轴承径向平面内Y轴径向载荷1 200 N, Z轴径向载荷0 N,轴向载荷0 N。分别对不同谐波参数下轴承进行动态仿真分析,获得各零件接触表面谐波参数对轴承振动影响关系。
2.3.1外滚道表面波纹度对轴承振动影响
设轴承内滚道及钢球表面为理想几何形状,仅外滚道表面存在加工形状误差。外滚道谐波阶次对轴承振动影响见图21。由图21可知,谐波阶次及幅值对轴承振动均有较大影响。谐波阶次一定时,幅值越大轴承振动越剧烈;随谐波阶次逐渐增大,轴承振动值呈递增趋势;谐波阶次为钢球数目整数倍时,轴承振动明显增大。与文献[4,15]结论一致。(z+1)次谐波与(z-1)次谐波对轴承振动影响基本相同。外滚道波纹度激励的轴承振动频率见图22。由图22知,当外滚道谐波阶次为9时,激励频率为592 Hz,与理论计算的变刚度频率fvc=zfc=597.36 Hz较接近,误差为0.9%;当外滚道谐波阶次为18时,激励频率为1 184.1 Hz,是变刚度频率的2倍。因此可得,外滚道谐波阶次l1=kz时,激励的轴承振动频率f=kfvc=kzfc,k=1,2…。


图15 轴承径向载荷与轴承振动的关系Fig.15Effectofradialloadsonvibrationvalue图16 轴承转速与轴承振动的关系Fig.16Effectofbearingrotatingspeedonvibrationvalue图17外载冲击变化量与轴承振动的关系Fig.17Effectofloadsimpactonvibrationvalue图18 外载冲击下内圈幅频图Fig.18Spectrumoftheinnerringatloadsimpact
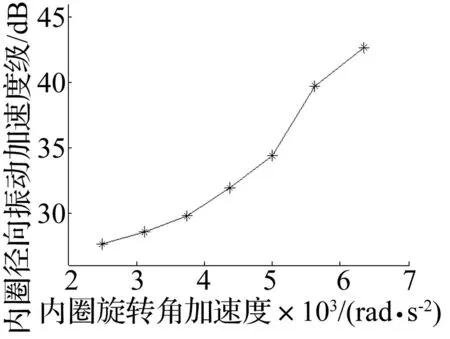
图19 转速冲击量与轴承振动的关系 Fig.19 Effect of speed impact on vibration value

图20 转速冲击下内圈频谱图 Fig.20 Spectrum of inner ring at impact of speed
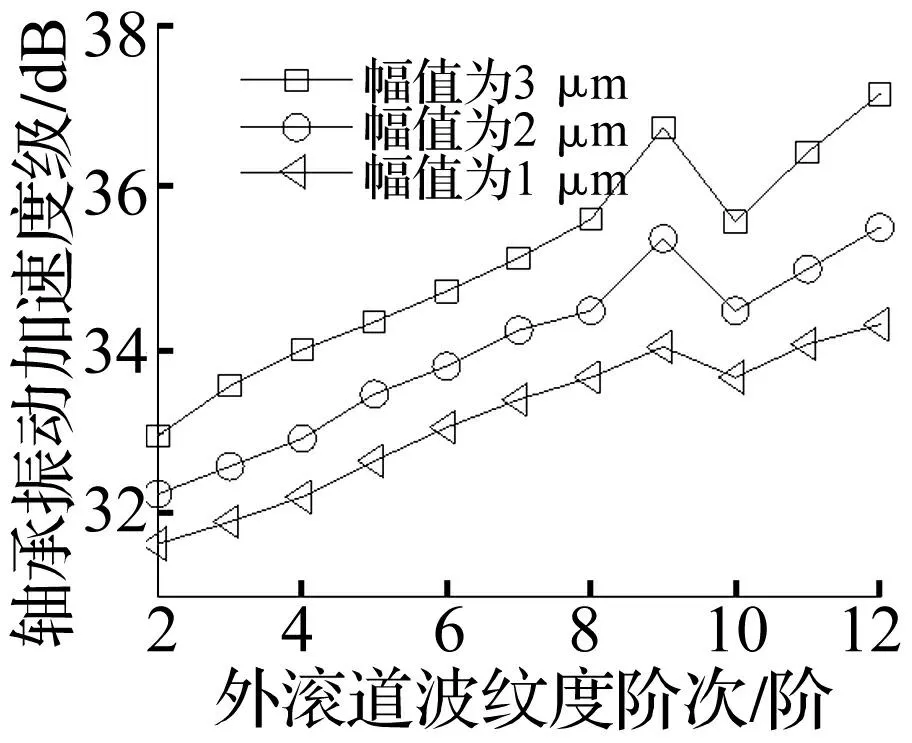
图21 外圈滚道波纹度对振动的影响 Fig.21 Effect of outer raceway surface waviness on vibration value
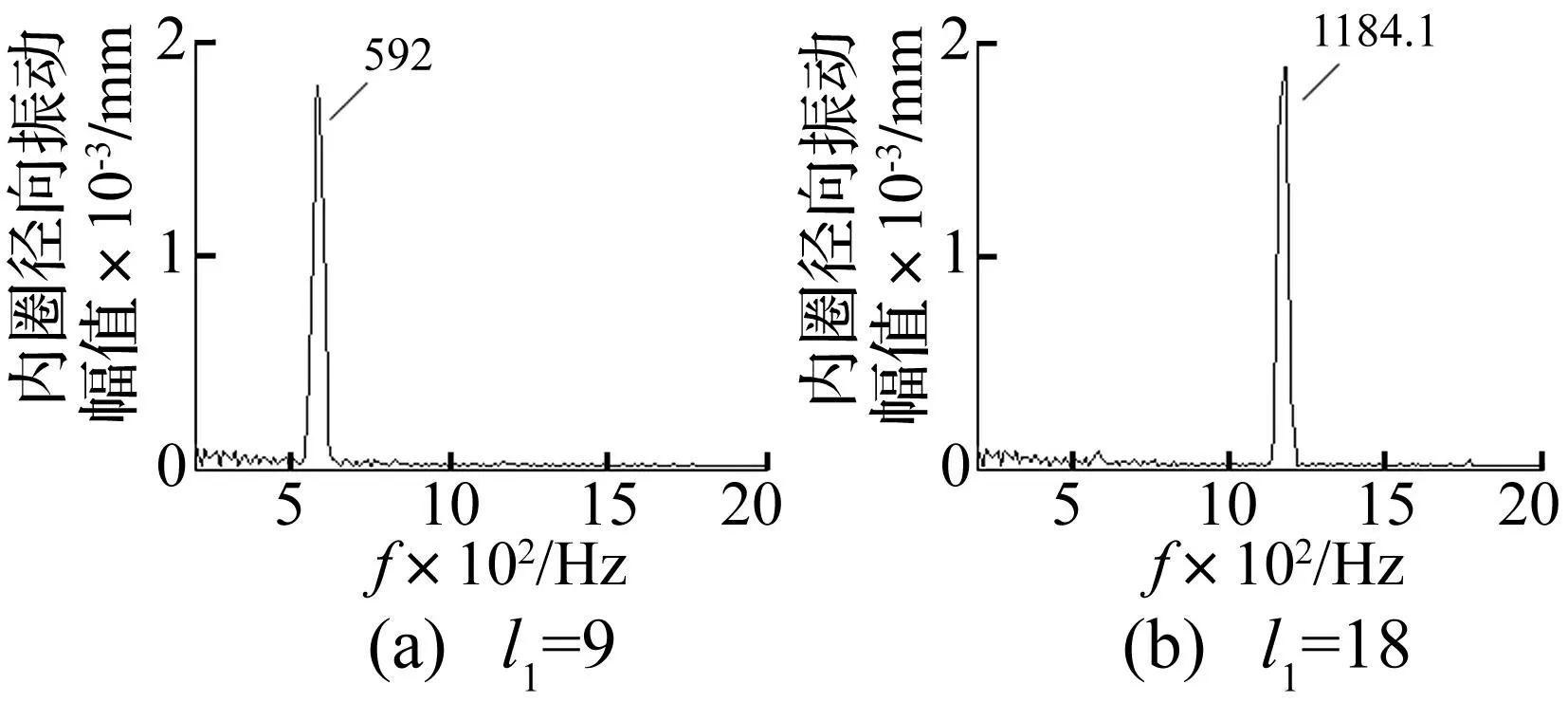
图22 外滚道波纹度频谱图 Fig.22 Spectrum of outer raceway surface waviness
2.3.2内滚道表面波纹度对轴承振动影响
设轴承外滚道及钢球表面为理想接触表面,内滚道波纹度阶次对轴承振动影响见图23。由图23可知,内滚道波纹度对振动影响规律与外滚道基本一致。图24为内滚道波纹度激励的轴承振动频率。可见当内滚道谐波阶次为9、激励频率756.8 Hz时,与fvc+fs=764.02 Hz较接近,误差仅0.94%,其中内圈旋转频率fs=n2/60;当内滚道谐波阶次为18、激励频率为1 342.8 Hz时,与2fvc+fs=1 361.5 Hz较接近,误差仅1.3%。因此可得,内滚道谐波阶次l2=kz时激励的轴承振动频率f=kfvc+fs,k=1,2…。
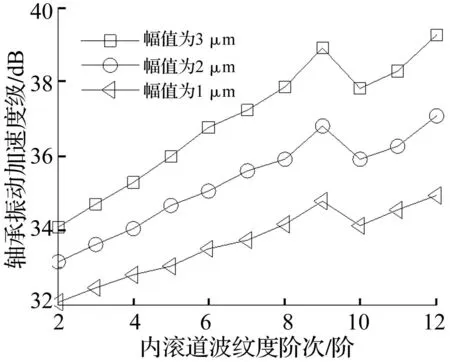
图23 内圈滚道波纹度对振动的影响 Fig.23 Effect of inner raceway surface waviness on vibration value
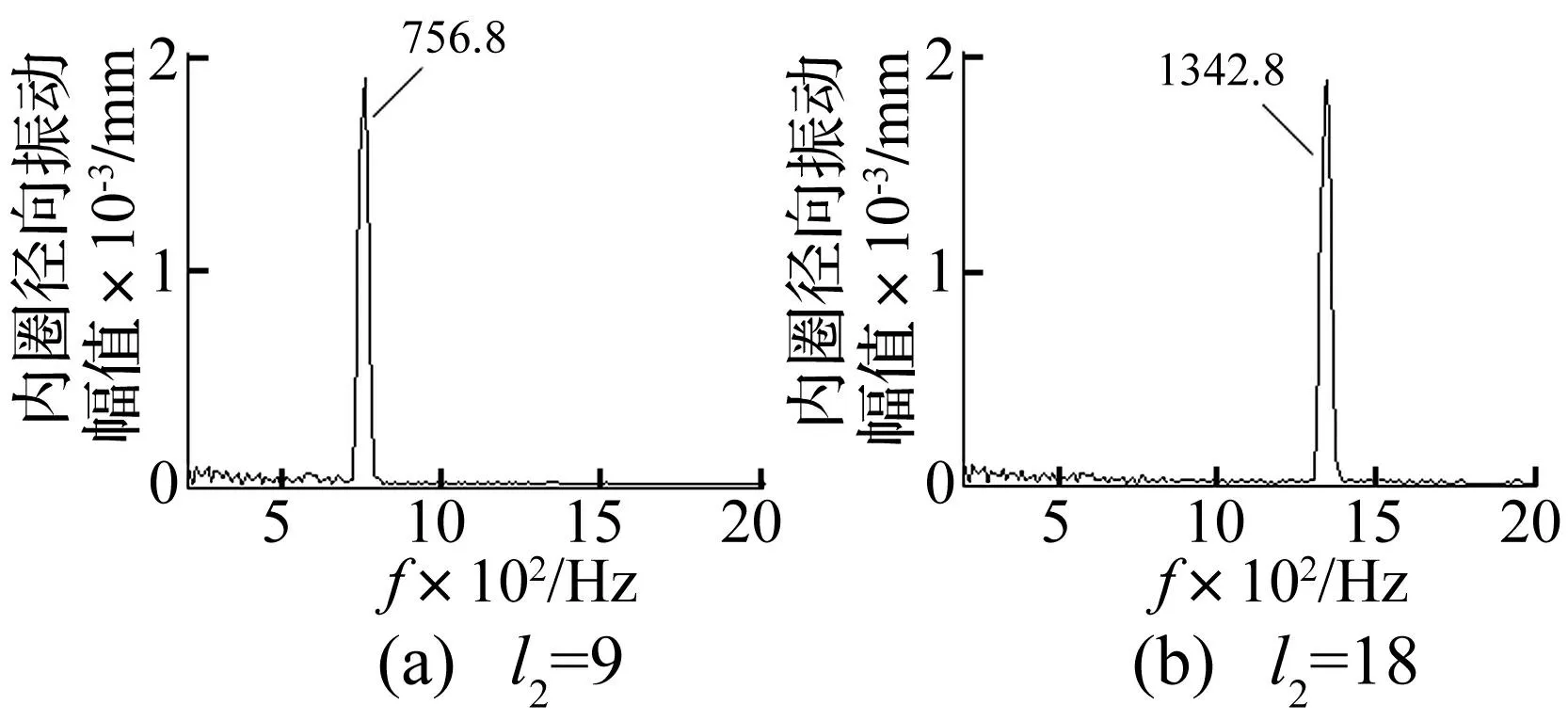
图24 内滚道波纹度频谱图 Fig.24 Spectrum of inner raceway surface waviness
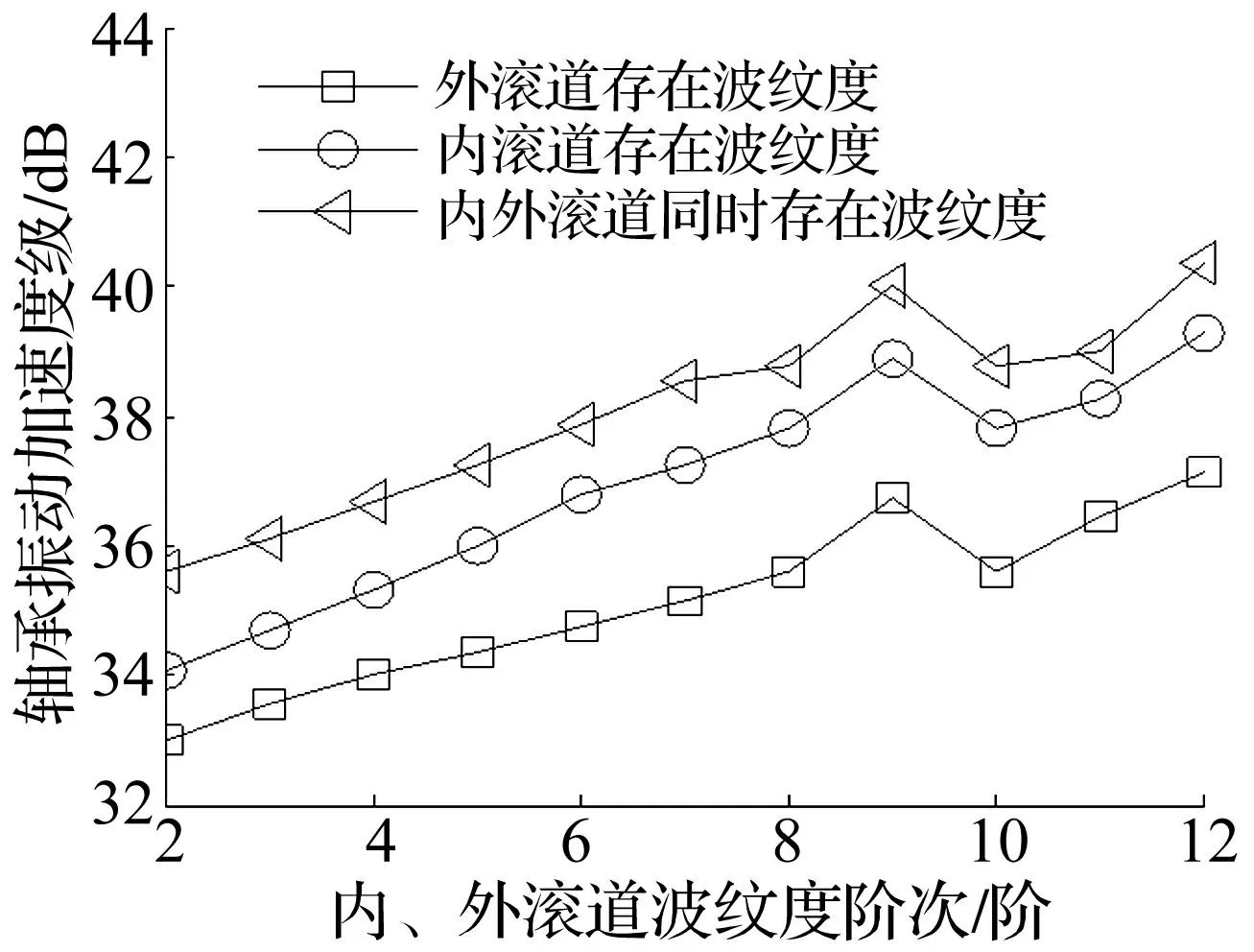
图25 内、外滚道波纹度对振动的影响 Fig.25 Effect of inner and outer raceway surface waviness on vibration value

图26 内、外滚道波纹度频谱图 Fig.26 Spectrum of inner and outer raceway surface waviness
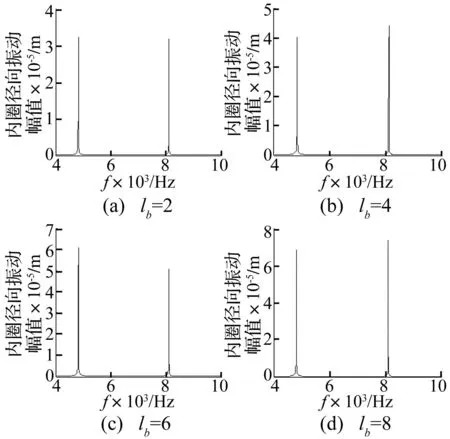
图27 钢球表面波纹度频谱图 Fig.27 Spectrum of ball surface waviness
2.3.3内、外滚道联合波纹度对轴承振动影响
设轴承钢球表面为理想接触表面,内、外滚道波纹度阶次对轴承振动影响见图25。由图25可知,轴承内、外滚道同时存在波纹度,轴承振动值较单一滚道波纹度激励的振动值大,内滚道更大。因内滚道与钢球均有6个自由度,且内圈为动圈。
内、外滚道同时存在波纹度时,激励的轴承振动频率见图26。由图26知,当l1=l2=kz,k=1,2时,轴承同时存在两种频率成分,即变刚度频率f=kfvc,k=1,2及内滚道波纹度激励出的派生频率f=kfvc+fs,k=1,2。
2.3.4钢球表面波纹度对轴承振动影响
设轴承内外滚道接触表面为理想表面,每个钢球表面波纹度分布一致。钢球表面谐波幅值为0.05 μm时谐波阶次(lb=2k,k=1,2,3…)对轴承径向振动幅值(一阶、二阶固有频率下)影响规律见图27。由图27看出,钢球表面谐波阶次不改变轴承一、二阶固有频率值,而振幅值随谐波阶次增加逐渐增大。
3结论
(1) 合理优化轴承结构参数,能从设计角度降低轴承振动、噪声。如选择具有对称结构的浪形保持架较尼龙保持架更利于降低轴承振动值;浪型保持架所具有的偏心距能进一步降低轴承振动值。
(2)对低噪音深沟球轴承施加一定轴向载荷,可有效降低轴承振动值,轴向载荷取(0.53%~0.89%)Cr为宜。
(3)轴承旋转套圈激励的轴承振动值更大,内、外滚道谐波阶次等于钢球数目整数倍时,轴承振动会明显加剧。内、外滚道激励谐波对应的激励频率为kzfc+fs及kzfc。故轴承加工过程中应控制谐波阶次产生。
参考文献
[1]赵联春. 球轴承振动的研究[D]. 杭州:浙江大学, 2003.
[2]Aktürk N,Uneeb M,Gohar R.The effects of number of balls and preload on vibrations associated with ball bearings[J]. Tribology, 1997, 119: 747-753.
[3]Wardle F P,Poon S . Rolling bearing noise,cause and cure[J].Chartered Mechanical Engineer, 1983, 30(7): 36-40.
[4]张耀强,陈建军,邓四二,等. 考虑表面波纹度的滚动轴承-转子系统非线性动力特性[J]. 航空动力学报, 2008, 23(9): 1731-1736.
ZHANG Yao-qiang,CHEN Jian-jun,DENG Si-er,et al. Nonlinear dynamic characteristics of a rolling bearing-rotor system with surface waviness[J]. Journal of Aerospace Power, 2008, 23(9): 1731-1736.
[5]Harsha S P. The effects of surface waviness and radial internal clearance[J]. Computational Methods in Engineering Science and Mechanics, 2006, 7: 91-111.
[6]夏新涛,颉潭成,邓四二,等. 基于谐波控制理论的滚动轴承噪声声压的函数[J].中国机械工程, 2002,13(15): 1277-1280.
XIA Xin-tao, JIE Tan-cheng, DENG Si-er, et al. Sound-pressure-level function of rolling bearing noise based on harmonic control theory[J].China Mechanical Engineering, 2002,13(15): 1277-1280.
[7]邓四二,腾弘飞,马付建,等. 航空发动机主轴轴承滚道表面光饰强化处理[J]. 航空动力学报, 2006, 21(3): 545-549.
DENG Si-er,TENG Hong-fei,MA Fu-jian,et al. Luster polish strengthening for race surface of the main shaft bearings of aeroenginc[J]. Journal of Aerospace Power, 2006, 21(3): 545-549.
[8]Wardle F P,Poon S Y. Vibration forces produced by waviness of the rolling surfaces of thrust loaded ball bearing,part 1:theory[J]. Proceedings of the Insitute of Mechanical Engineers, 1988, 202(C5): 305-312.
[9]Wardle F P. Vibration forces produced by waviness of the rolling surfaces of thrust loaded ball bearing,part 2:experimental validation[J]. Proceedings of the Insitute of Mechanical Engineers, 1988, 202(C5): 313-319.
[10]Aktürk N.The effect of waviness on vibrations associated with ball bearings[J]. ASME Journal of Tribology, 1999, 121: 667-677.
[11]Jang G, Jeong S W. Vibration analysis of a rotating system due to the effect of ball bearing waviness [J].Journal of Sound and Vibration, 2004,269:709-726.
[12]邓四二,李兴林,汪久根. 角接触球轴承摩擦力矩波动性分析[J]. 机械工程学报, 2011, 47(19): 49-57.
DENG Si-er,LI Xing-lin,WANG Jiu-gen. Analysis on the friction torque fluctuation of angular contact ball bearings[J]. Journal of Mechanical Engineer, 2011,47(19): 49-57.
[13]邓四二,梁波.双半套圈球轴承分析与设计研究报告[R].洛阳:洛阳轴承研究所,2005.
[14]杨晓蔚,李红涛.滚动轴承振动与噪声的相关性解析[J]. 轴承, 2011, 7: 53-56.
YANG Xiao-wei,LI Hong-tao. Analysis on correlation between vibration and noise of rolling bearings[J]. Bearing, 2011, 7: 53-56.
[15]Jang G, Jeong S W. Analysis of a ball bearing with waviness considering the centrifugal force and gyroscopic moment of the ball[J]. Tribology, 2003, 125: 487-498.


