谐波干扰下海上风机结构工作模态识别

第一作者董霄峰男，博士生，1986年8月生

通信作者练继建男，教授，博士生导师，1965年8月生

谐波干扰下海上风机结构工作模态识别

董霄峰，练继建，杨敏，王海军(天津大学水利工程仿真与安全国家重点实验室，天津300072)

摘要：针对海上风力发电机组高转速叶轮对风机结构会造成强烈的周期性激励，而该强谐波作用往往会淹没响应中的结构模态信息，增加识别结构工作模态参数难度问题，以某海上风电试验样机振动响应原型观测信号为研究对象，采用基于改进特征系统实现法(Eigensystem Realization Algorithm，ERA)与概率密度函数法(Probability Density Function，PDF)结合的工作模态识别方法及判定思路，剔除不同工况下转频、倍频谐波成分干扰，实现风机结构多阶工作模态参数有效识别。该方法不仅能有效避免谐波干扰以获取结构的真实工作模态，同时对海上风机结构运行安全性实时在线监测、评估具有较好的工程适用性。

关键词：海上风电；工作模态识别；谐波干扰；改进ERA；概率密度函数

基金项目：国家国际科技合作专项资助(2012DFA70490)；国家高技术研究发展计划(863计划)资助(2012AA051702)；天津市应用基础及前沿技术研究计划(青年基金项目)资助(12JCQNJC04000)；国家创新研究群体科学基金资助(51021004)

收稿日期：2014-03-19修改稿收到日期：2014-04-30

中图分类号:TK8文献标志码：A

Operational modal identification of an offshore wind turbine structure under harmonic interference

DONGXiao-feng,LIANJi-jian,YANGMin,WANGHai-jun(State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)

Abstract:It is difficult to identify the operational modal parameters of an offshore wind turbine structure accurately because the structural modal information in its responses is buried by the strong recurring harmonic excitation induced from the wind turbine’s impeller with high rotating speed. In order to solve the problem of structural operational modal identification, a method combining the modified eigensystem realization algorithm (ERA) with the probability density function (PDF) was proposed here. Subsequently, the interference coming from the rotating frequencies and frequency multiplication was eliminated and the effective identification for the multi-operational modal parameters of a certain offshore wind turbine test prototype was achieved based on the measured signals under different operational conditions. It was shown that this approach can not only avoid the strong harmonic interference so as to obtain the real structural operational modes effectively, but also has a better engineering applicability in online real-time monitoring and evaluation of the structural operational security for offshore wind turbine structures.

Key words:offshore wind power; operational modal identification; harmonic interference; modified eigensystem realization algorithm (ERA); probability density function (PDF)

结构工作模态参数可用于表征结构运行工况体现的与该工作状态相匹配的动态特性，是判断结构运行安全性的重要动态指标[1]。对配有旋转设备的运行结构而言，结构工作模态与其固有模态间存在一定差别[2]。因此，正确掌握结构工作模态特性有助于提高激振力与结构间共振问题判断的准确程度，进而避免出现结构运行安全隐患。

对高转速运行下海上风机结构工作模态的识别，主要难点在于如何既能剔除与结构模态频率相近的谐波成分在结构系统特征矩阵中产生的干扰，又能在模态识别中区分高阶模态信息与未知的谐波倍频成分。因此，本文考虑海上风机结构在高转速工况下谐波激励对振动响应影响特性，假设风机在短时运行状态下谐波频率具有稳定时不变特性，采用基于改进特征系统实现法(ERA)与概率密度函数法(PDF)联合多阶模态识别方法并首次应用在海上风机结构的工作模态参数识别中。基于实测信号确定响应中存在的主要干扰谐波频率，采用改进ERA法完成模态初步识别，实现真实模态与谐波模态同时提取；通过所得多阶模态频率对应时域信息的概率密度函数分布特征区分真实工作模态与谐波倍频成分引起的虚假模态。该工作模态联合识别方法不仅能有效避免强烈转频谐波成分干扰，准确获得结构工作模态信息，对高阶模态与未知谐波虚假模态的分辨也有显著效果。

1理论方法与识别流程

1.1考虑谐波影响的改进ERA法

据文献[9]，基于自然激励法(NExT)及ERA法对受环境激励的大型工程结构进行模态识别时，可利用实测结构两测点间响应信号的互相关函数代替脉冲响应函数构建Hankel矩阵。k时刻相应的Hankel矩阵[10]可写为

H(k)=

(1)

据文献[11]，不同测点信号间互相关函数可表示为以各阶结构模态频率与阻尼比为参数进行衰减的不同正弦信号叠加，其中也应包括受稳定持续谐波激励影响而产生的谐波模态及倍频模态信息。当环境荷载激励下结构随机振动中混有频率已知且临近结构模态信息的谐波成分，且谐波成分在Hankel矩阵中占较大比重时，结构自身模态信息会淹没于谐波干扰中，使据ERA法原理在对式(1)进行分解处理后所得结构振动系统特征矩阵中结构模态信息出现混淆，影响工作模态识别的准确性。

为在工作模态识别过程中充分体现谐波成分而实现在特征矩阵中与结构模态信息分离目的，需在传统ERA法基础上分别构造谐波Hankel矩阵Hh(0)及Hh(1)，并将其作为矩阵的延长项与式(1)中原始Hankel矩阵进行重构，所得新的扩展Hankel矩阵为

(2)

式中：H(0)，H(1)为原始Hankel矩阵在0，1时刻的体现，可由实测结构不同位置振动响应间互相关函数构成，矩阵维度m×n；Hh(0)，Hh(1)为原始Hankel矩阵的延长矩阵，代表响应中已知的主要谐波成分。

考虑谐波模态具有零阻尼比特性，谐波成分在响应中稳定无衰减，因此延长矩阵可写为标准正弦及余弦函数形式[11]，即

(3)

Hh(1)=

(4)

式中：h为响应中已知谐波数量。

对经加入谐波成分后延长的扩展Hankel矩阵，所含结构模态信息不会发生变化，因此对重构的Hankel矩阵He(0)进行奇异值分解，得

He(0)=UeΣeVeT=QeWe

(5)

式中：Σe为(m+2h)×n维奇异值对角矩阵；Ue，Ve分别为(m+2h)×(m+2h)维、n×n维正交矩阵，分别为左右奇异值向量矩阵。矩阵Qe，We可写为

Qe=UeΣe1/2，We=Σ1/2eVeT

(6)

若定义结构振动系统自由度为dof，谐波频率个数为h，则结构振动系统重构后的总自由度数应为N=dof+h，将上式中各矩阵按2N行或列截断，可得新矩阵为

(7)

式中：Qe2N，We2N分别为截断后新观测矩阵及控制矩阵；Ue2N，Ve2N分别为Ue，Ve前2N阶列矩阵；Σe2N为Σe前2N阶方阵，含系统矩阵中有用信息。

由系统最小实现理论可得体现不同模态信息特征矩阵Are的求解方程式，即

He(1)=Qe2NAreWe2N

(8)

基于以上各式，可得结构振动系统完整的特征矩阵Are，对其进行特征值求解所得模态信息既包括结构自身模态成分也应该包括来自叶轮转动引起的转频谐波成分。

1.2概率密度函数法

概率密度函数法的理论基础为随机响应与谐波响应具有不同的统计特性，其概率密度分布函数曲线具有较明显有效的分辨能力。对随机振动响应而言，任意独立同分布的随机变量X1，X2，…，Xn之和对应的分布函数[12]可表示为

(9)

由上式知，当任意结构受到足够多的独立随机荷载激励时(如风、浪等环境荷载对风机结构的联合作用)，结构总体响应可认为是多个随机激励下产生响应的线性叠加，其概率密度函数近似服从高斯分布，在函数分布曲线中仅存在一个明显峰值。对谐波响应的概率密度分布，设已知谐波响应y=g(x)=asin(ωx)，将x的概率密度视为不变值fX，则谐波响应概率密度函数为

(10)

当y→±a时，零均值谐波响应的概率密度函数将趋近于∞，分布曲线中会出现两个不同峰值。若谐波响应幅值恒定，则对任意频率ω式(10)均成立。据随机、谐波响应在概率密度函数分布特性的差异，完成工作模态识别后可利用带通滤波原理构造适宜滤波器，以各阶识别频率平均值作为中心频率，各阶识别频率范围作为通带宽度，将各阶识别模态所对应频域内的时域信息进行分离，进而通过不同频率对应的概率密度函数分布形式判断所得结构各阶模态的真伪。

1.3强谐波影响下结构工作模态识别流程

基于以上理论介绍，据实测高转速工况下短时谐波激励对海上风机结构振动响应影响特性，可确定该结构强谐波激励影响下工作模态参数识别流程，即:①选取风机高转速运行典型工况，假定振动信号中全部频分为结构模态成分，利用NExT法获取测点间互相关函数，构造用于模态识别的Hankel矩阵；②确定影响结构振动的主要已知谐波频率成分，构造扩展谐波Hankel矩阵并加入②中建立考虑谐波影响的Hankel矩阵；③通过改进ERA法求解结构振动系统完整的特征矩阵，同时获得结构模态参数与谐波模态信息；④采用概率密度函数法对识别各阶模态对应的时域信号进行分辨，以区分结构高阶模态信息与谐波模态成分。

该识别流程可将改进ERA法与概率密度函数法结合，剔除、分辨谐波干扰成分，实现结构工作模态参数的准确识别。

2工程概况与结构频响特性

2.1工程概况

图1　现场测点布置示意图 Fig.1 Layout of the field testing

以某海上风电试验样机为例说明本文采用模态识别与判定方法的适用性。测试风电样机基础采用复合式筒型基础形式[13-14]，风机机组为额定功率2.5 MW三叶片直驱型机组，叶轮额定转速18 r/min。风机轮毂高度80 m，塔筒总长77.5 m，分三段式安装，机舱与塔筒及相邻塔筒间均设有工作平台。按塔筒内部沿高度方向布置5个测点，具体位置见图1。测试选DPS型地震式低频振动位移传感器，频响范围最低达0.1 Hz，为三向测振，满足采集结构低频多向振动信号试验目的。信号采样频率200 Hz，每组工况在叶轮转速稳定条件下测试60 s。

2.2结构频响特性

风速9.0 m/s时海上风机结构停机状态塔筒顶部1#测点Z向动态位移时程与功率谱密度曲线见图2。由图2看出，停机状态下结构振动响应主频率约0.33 Hz。考虑此时风机叶轮未转动，风机结构仅受包括风、浪等环境荷载激励作用，结构响应中的频率特征应为结构自身的振动属性，因此可确定该风电样机的一阶结构模态频率约为0.33 Hz。

叶轮转速为16 r/min及18 r/min时，风机塔筒顶部1#测点运行状态Z向动态位移时程线及功率谱密度曲线见图3、图4。由二图看出，转速为16 r/min时结构振动主频率为0.267 Hz，而转速增加到18 r/min时响应主频则变为0.30 Hz。两种转速下结构顶部振动优势频率恰与该工况叶轮转频相同而非结构模态频率。说明风力发电机达到高转速运行时，风机结构振动响应体现的信息主要是其在叶轮强制作用影响下做受迫振动对应的频率。而持续环境激励下体现的结构模态频率信息由于与谐波频率较接近，且较谐波频率能量小而被埋没于后者的频带范围内，结构自身模态信息无法从频谱中获得。因此，通过有效方法从结构振动响应中提取、区分真实工作模态信息具有重要意义。

图2 停机状态下位移时程及功率谱Fig.2DisplacementhistoryandPSDcurveatstandstill图3 16r/min时位移时程及功率谱Fig.3DisplacementhistoryandPSDcurvein16r/min图4 18r/min时位移时程及功率谱Fig.4DisplacementhistoryandPSDcurvein18r/min

3海上风机结构工作模态识别

2.2节中两种运行工况为海上风机受强谐波激励影响下结构振动典型工况。由于响应信号中仅有一种主要频率且频带较窄，则可近似认为风机所受谐波激励在运行时段内具有稳定不变特性。为说明本文所用方法的适用性，以位于塔筒底部振动最弱的5#测点为参考点，通过NExT法计算1#与5#测点Z向振动信号间互相关函数作为工作模态识别中构造Hankel矩阵的基本信息[15]；再以振动响应频谱中的叶轮转频作为主要谐波影响成分加入Hankel矩阵中，分别采用改进前后ERA法完成结构工作模态的初步识别；利用概率密度函数法区分、剔除高阶模态信息及未知谐波倍频成分进，以保证识别结构模态的准确性。

叶轮转速为16 r/min及18 r/min时，应用改进前后的ERA法识别所得结构一阶模态频率随Hankel矩阵行数变化示意图见图5、图6。由二图看出，塔筒顶部1#测点响应频域特性(实线)表现出结构所受强迫振动的叶轮激励频率；方块为通过传统ERA法识别所得模态频率，表明所受该工况下谐波频率严重影响，一阶频率与叶轮转频较接近，远远偏离结构自身模态频率位置(0.33 Hz附近)。因此对高转速下振动响应信号，忽视谐波频率影响直接采用传统ERA方法进行模态识别将无法获得结构准确的真实模态信息。

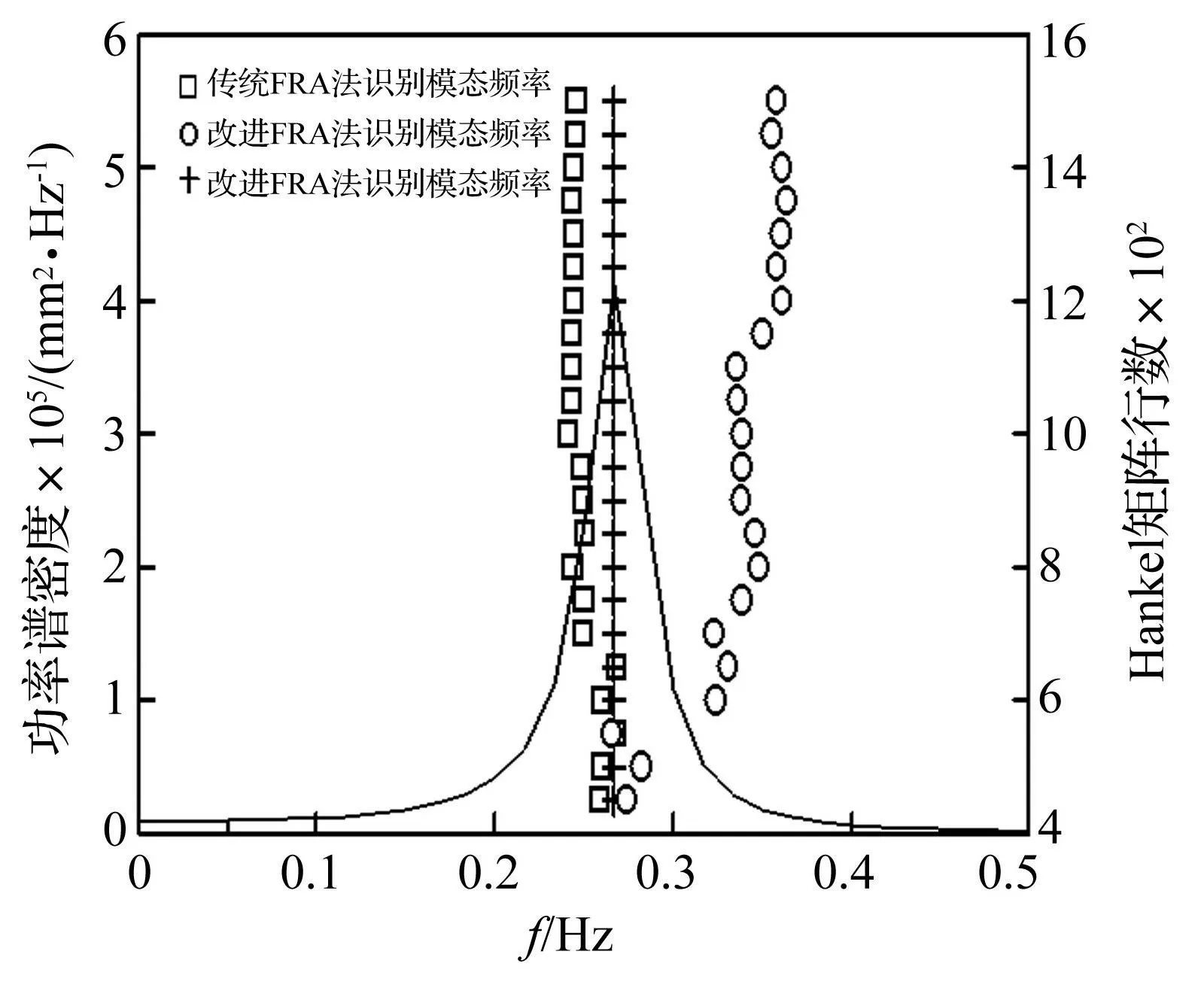
图5　转速16 r/min时识别一阶模态频率稳定图 Fig.5 Stabilization diagram of first modal frequency in 16 r/min

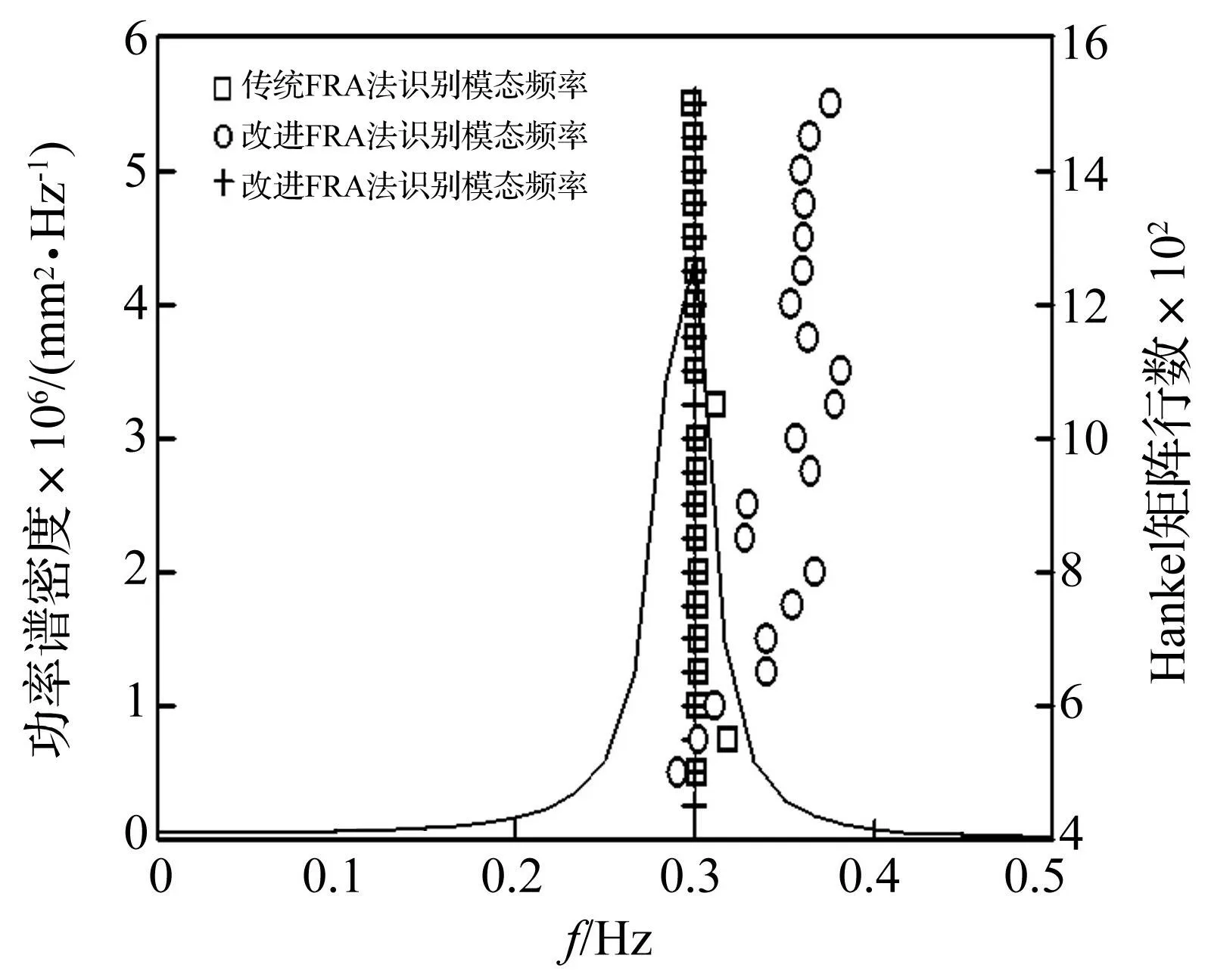
图6　18 r/min时识别一阶模态频率稳定图 Fig.6 Stabilization diagram of first modal frequency in 18 r/min

在已知主要干扰谐波频率前提下，采用考虑谐波影响、改进ERA法识别结果则能较有效区分响应中主要谐波模态与结构一阶工作模态成分。图5、图6中圆圈即为通过改进ERA方法识别所得结构一阶模态频率。随Hankle矩阵行数变化，频率识别值均接近且多数大于理论值0.33 Hz，虽行数在600以下时识别结果略有偏差，但工作模态识别结果整体稳定可靠。该结果不仅验证结构工作模态与固有模态间存在差异，且与转频间偏差较大，结构运行无共振隐患。二图中十字为通过改进ERA法识别所得谐波模态频率，与实测信号响应中混有的谐波成分保持一致，识别阻尼比满足谐波模态零阻尼比特征。

表1为两种运行工况下识别获得前四阶工作模态参数信息。由表1看出，0.267 Hz与0.30 Hz应为风机运行引起强谐波激励出现的谐波模态，其频率与叶轮转动频率保持一致且对应的阻尼比为零。通过改进ERA法所得5种模态成分，相应频域范围分别为0.33～ 0.38 Hz、0.92～0.93Hz、1.33～1.40 Hz、2.11～2.16 Hz及2.21～2.26 Hz，各阶模态真伪性尚需通过概率密度函数曲线特性判断。

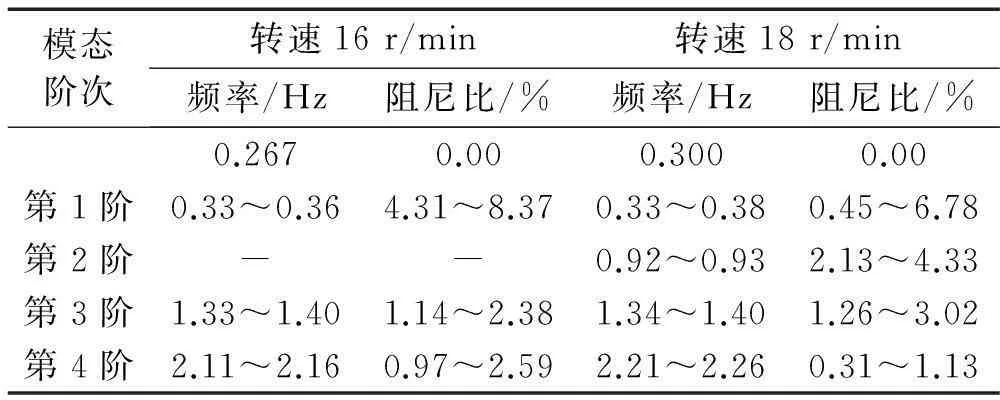
表1　两种运行工况下改进ERA法识别所得各阶模态信息汇总表

风机叶轮转速稳定在16 r/min时模态识别获得各阶频率区域所对应时域滤波信号概率密度分布函数曲线见图7。由图7看出，频率在2.13～2.16 Hz范围对

应的概率密度分布函数曲线呈两个较明显的峰值分布特征，说明此阶模态的产生与响应中谐波成分有关，为由转频谐波的倍频成分所致虚假模态。其余两阶模态频率对应的概率密度分布函数曲线基本保持高斯分布特性，即具有一个明显分布峰值，可判定此两阶频率对应模态为海上风机结构真实工作模态。

基于概率密度函数的模态分辨方法，可判断出风机叶轮运行转速稳定在18 r/min时，识别获得第一、三阶工作模态符合结构随机振动特性，识别模态频率应为结构自身工作模态频率。而对第二、四阶模态主要体现谐波响应的振动特性，说明该两阶模态为由谐波倍频成分激励引起的谐波模态。识别所得第二阶模态频率范围0.92～0.93 Hz正好对应该工况下叶轮转频的3倍频，而四阶2.25 Hz则可能为由多倍转频引起的虚假模态。

图7　16 r/min时各模态对应概率密度分布函数曲线 Fig.7 PDF curve corresponding to each order modes in 16 r/min

4结论

本文针对高转速运行状态的海上风机结构受叶轮转动所致强谐波激励影响、造成无法准确获得结构工作模态问题，以某海上风力发电试验样机原型观测振动数据为研究对象，引入基于改进ERA法与概率密度函数法的联合方法实现结构工作模态的准确识别，结论如下：

(1)在主要干扰谐波频率已知条件下，通过改进ERA法能有效分离已知谐波模态与结构真实模态。对结构工作模态频率与谐波干扰频率较接近的海上风机结构尤为适用。

(2)据随机振动响应与谐波响应统计特征，利用两者在概率密度函数分布特性上的差异判断识别模态中倍频谐波成分具有较好实用性，已在工程实践中获得验证。

(3)由本文方法识别出海上风机结构前两阶工作模态频率范围为0.33～0.38及1.33～1.40，结构阻尼比均在合理范围，可保障风机结构运行安全性。说明该方法对海上风机多阶结构工作模态信息实时识别及结构运行安全性在线监测与评估精度及工程适用性均较好。

参考文献

[1]Carne T G,James G H. The inception of OMA in the development of modal testing technology for wind turbines[J]. Mechanical Systems and Signal Processing,2010,24:1213-1226.

[2]Hansen M H, Thomsen K, Fuglsang P,et al. Two methods for estimating aeroelastic damping of operational wind turbine modes from experiments [J]. Wind Energy,2006, 9: 179-191.

[3]Peeters B,Cornelis B,Janssens K. Removing disturbing harmonics in operational modal analysis[C]. In Proc. IOMAC,Copenhagen Denmark,2007.

[4]Jacobsen N J, Andersen P, Brincker R. Eliminating the influence of harmonic components in operational modal analysis [C]. IMAC XXV Conference, 2007.

[5]张义民,张守元,李鹤,等.运行模态分析中固有模态和谐波模态区分方法研究[J].振动与冲击,2009, 28(1):64-67.

ZHANG Yi-min, ZHANG Shou-yuan,LI He,et al. Study on method of distinguishing the natural modes from harmonic modes in operational modal analysis[J]. Journal of Vibration and Shock, 2009, 28(1):64-67.义民,张守元,李鹤,等.运行模态分析中固有模态和谐波模态区分方法研究[J].振动与冲击,2009, 28(1):64-67.

ZHANG Yi-min, ZHANG Shou-yuan,LI He,et al. Study on method of distinguishing the natural modes from harmonic modes in operational modal analysis[J]. Journal of Vibration and Shock, 2009, 28(1):64-67.

[6]Brincker R, Andersen P, MØller N. An indicator for separation of structural and harmonic modes in output-only modal testing[C]. International Modal Analysis Conference (IMAC XVIII), San Antonio, TX, Society for Engineering Mechanics, Bethel, CT, 2000: 1649-1654.

(下转第172页) T G,James G H. The inception of OMA in the development of modal testing technology for wind turbines[J]. Mechanical Systems and Signal Processing,2010,24:1213-1226.

[2]Hansen M H, Thomsen K, Fuglsang P,et al. Two methods for estimating aeroelastic damping of operational wind turbine modes from experiments [J]. Wind Energy,2006, 9: 179-191.

[3]Peeters B,Cornelis B,Janssens K. Removing disturbing harmonics in operational modal analysis[C]. In Proc. IOMAC,Copenhagen Denmark,2007.

[4]Jacobsen N J, Andersen P, Brincker R. Eliminating the influence of harmonic components in operational modal analysis [C]. IMAC XXV Conference, 2007.

[5]张义民,张守元,李鹤,等.运行模态分析中固有模态和谐波模态区分方法研究[J].振动与冲击,2009, 28(1):64-67.

ZHANG Yi-min, ZHANG Shou-yuan,LI He,et al. Study on method of distinguishing the natural modes from harmonic modes in operational modal analysis[J]. Journal of Vibration and Shock, 2009, 28(1):64-67.义民,张守元,李鹤,等.运行模态分析中固有模态和谐波模态区分方法研究[J].振动与冲击,2009, 28(1):64-67.

ZHANG Yi-min, ZHANG Shou-yuan,LI He,et al. Study on method of distinguishing the natural modes from harmonic modes in operational modal analysis[J]. Journal of Vibration and Shock, 2009, 28(1):64-67.

[6]Brincker R, Andersen P, MØller N. An indicator for separation of structural and harmonic modes in output-only modal testing[C]. International Modal Analysis Conference (IMAC XVIII), San Antonio, TX, Society for Engineering Mechanics, Bethel, CT, 2000: 1649-1654.

[7]Mohanty P,Rixen D J. Identifying mode shapes and modal frequencies by operational modal analysis in the presence of harmonic excitation [J].Society for Experimental Mechanics, 2005, 45(3): 213-220.

[8]Mohanty P,Rixen D J. Modified SSTD method to account for harmonic excitations during operational modal analysis[J]. Mechanism and Machine Theory, 2004, 39: 1247-1255.

[9]练继建,李火坤,张建伟. 基于奇异熵定阶降噪的水工结构振动模态ERA识别方法[J].中国科学E辑,2008,38(9):1398-1413.

LIAN Ji-jian, LI Huo-kun, ZHANG Jian-wei. ERA modal identification method for hydraulic structures based on order determination and noise reduction of singular entropy[J]. Science in China Series E: Technological Sciences, 2008, 38(9): 1398-1413.

[10]Li P, Hu S L J, Li H J. Noise Issues of modal identification using eigensystem realization algorithm[J]. Procedia Engineering, 2011, 14:1681-1689.

[11]Mohanty P,Rixen D J. Modified ERA method for operational modal analysis in the presence of harmonic excitations[J]. Mechanical Systems and Signal Processing, 2006, 20:114-130.

[12]李怀鹏.运行模态分析中周期性激励识别方法研究[D].南京：南京航空航天大学，2010.

[13]Lian Ji-jian, Sun Li-qiang, Zhang Jin-feng et al. Bearing capacity and technical advantages of composite bucket foundation of offshore wind turbines [J]. Transactions of Tianjin University, 2011, 17: 132-137.

[14]Lian Ji-jian, Ding Hong-yan, Zhang Pu-yang,et al. Design of large-scale prestressing bucket foundation for offshore wind turbines[J].Transactions of Tianjin University,2012,18:79-84.

[15]练继建,张建伟,李火坤,等. 泄洪激励下高拱坝模态参数识别研究[J].振动与冲击,2007, 26(12):101-105.

LIAN Ji-jian, ZHANG Jian-wei, Li Huo-kun,et al. Study on modal parameter identification of high arch dam under flood discharge excitation[J]. Journal of Vibration and Shock, 2007, 26(12):101-105. P,Rixen D J. Identifying mode shapes and modal frequencies by operational modal analysis in the presence of harmonic excitation [J].Society for Experimental Mechanics, 2005, 45(3): 213-220.

[8]Mohanty P,Rixen D J. Modified SSTD method to account for harmonic excitations during operational modal analysis[J]. Mechanism and Machine Theory, 2004, 39: 1247-1255.

[9]练继建,李火坤,张建伟. 基于奇异熵定阶降噪的水工结构振动模态ERA识别方法[J].中国科学E辑,2008,38(9):1398-1413.

LIAN Ji-jian, LI Huo-kun, ZHANG Jian-wei. ERA modal identification method for hydraulic structures based on order determination and noise reduction of singular entropy[J]. Science in China Series E: Technological Sciences, 2008, 38(9): 1398-1413.

[10]Li P, Hu S L J, Li H J. Noise Issues of modal identification using eigensystem realization algorithm[J]. Procedia Engineering, 2011, 14:1681-1689.

[11]Mohanty P,Rixen D J. Modified ERA method for operational modal analysis in the presence of harmonic excitations[J]. Mechanical Systems and Signal Processing, 2006, 20:114-130.

[12]李怀鹏.运行模态分析中周期性激励识别方法研究[D].南京：南京航空航天大学，2010.

[13]Lian Ji-jian, Sun Li-qiang, Zhang Jin-feng et al. Bearing capacity and technical advantages of composite bucket foundation of offshore wind turbines [J]. Transactions of Tianjin University, 2011, 17: 132-137.

[14]Lian Ji-jian, Ding Hong-yan, Zhang Pu-yang,et al. Design of large-scale prestressing bucket foundation for offshore wind turbines[J].Transactions of Tianjin University,2012,18:79-84.

[15]练继建,张建伟,李火坤,等. 泄洪激励下高拱坝模态参数识别研究[J].振动与冲击,2007, 26(12):101-105.

LIAN Ji-jian, ZHANG Jian-wei, Li Huo-kun,et al. Study on modal parameter identification of high arch dam under flood discharge excitation[J]. Journal of Vibration and Shock, 2007, 26(12):101-105.