基于非圆弧理论的平整机轧制力简化模型

基于非圆弧理论的平整机轧制力简化模型

王东城1,2王芸红1

1.燕山大学国家冷轧板带装备及工艺工程技术研究中心，秦皇岛，0660042.燕山大学亚稳材料制备技术与科学国家重点实验室，秦皇岛，066004

摘要：针对目前带钢平整机轧制力模型的缺点，综合考虑带材的弹性变形与塑性变形，基于非圆弧轧辊理论的大量计算结果，回归得到一套冷带钢平整机轧制力简化模型。该模型可用于干平整或湿平整轧机设计、轧制规程制定。4个典型算例的计算结果表明，简化模型与非圆弧轧辊理论计算结果一致。最终通过2套平整轧机的实测轧制力验证了简化模型的正确性。

关键词：带钢；平整机；轧制力；非圆弧理论；简化模型

中图分类号：TG335

收稿日期：2015-01-06

基金项目：河北省高等学校科学技术研究项目(ZD2014034)；燕山大学青年自主研究计划资助项目(14LGA003)

作者简介：王东城，男，1981年生。燕山大学国家冷轧板带装备及工艺工程技术研究中心、燕山大学亚稳材料制备技术与科学国家重点实验室副教授。主要研究方向为板带轧制理论。获得省部级一等奖3项。发表论文20余篇。王芸红，女，1988年生。燕山大学国家冷轧板带装备及工艺工程技术研究中心硕士研究生。

Simplified Rolling Force Model for Temper Rolling Mill Based on Non Circular Arc Theory

Wang Dongcheng1,2Wang Yunhong1

1.National Engineering Research Center for Equipment and Technology of Cold Rolling Strip，

Yanshan University，Qinhuangdao，Hebei，066004

2.State Key Laboratory of Metastable Materials Science and Technology，

Yanshan University，Qinhuangdao，Hebei，066004

Abstract:In view of the disadvantages of the rolling force model for temper rolling mill, considering the strip’s elastic and plastic deformation, a simplified rolling force model for cold temper rolling mill was put forward based on a lot of calculation results of non circular arc theory. The simplified rolling force model could be used to mill designing and developing procedures for both dry and wet temper rolling mill. The results of 4 typical examples show that the simplified rolling force model is in well agreement with the non circular arc theory. Finally, the simplified model’s correctness was verified by the measured rolling force of 2 temper rolling mills.

Key words: strip; temper rolling mill; rolling force; non circular arc theory; simplified model

0引言

平整轧制是带钢生产的重要工序，国内外学者针对平整轧制进行了大量研究，其主要工作包括辊型优化[1]、板形控制[2]、表面粗糙度控制[3]、色差控制[4]等。由于平整轧制的压下量很小，其变形机理与普通轧制存在很大不同，因此普通的轧制力模型很难精确预报平整轧制力[5]。于是，国内外学者对平整机轧制力模型也进行了大量研究。Roberts[6]提出专用于干平整的轧制力显式模型，该模型物理意义明确、计算简单，获得了大量应用。连家创[7]考虑弹性变形区与轧辊弹性压扁的特殊性，建立了冷轧薄板轧制压力模型(可用于计算平整轧制力[8])。Fleck等[9]提出了非圆弧轧辊理论，以之为基础建立了冷轧极薄带材的轧制力模型。该模型得到大量引用，并被用于平整轧制力[10-11]。杜凤山等[12]采用有限元方法分析了平整轧制；魏立群等[13]采用神经网络建立了平整机轧制力模型；白振华等[14]、薛栋梁等[15]通过理论建模与参数自学习相结合的方式，建立了平整机轧制力在线模型。

总体而言，平整轧制力的建模方法可以分为三类：机理方法[6-12]、智能方法[13]、机理或智能模型与参数自学习相结合的方法[14-15]。上述三类建模方法各有优缺点。第一类方法的普适能力最强，但通常需要进行复杂的迭代计算，计算时间长，容易发散。第二类方法需要大量的生产数据作为训练样本。当样本收集不全时，很难拓展应用。同时，平整轧制力实测数据的分散性较大(当全部的输入参数相同或相近时，实际采集到的轧制力可能相差较大)，对神经网络进行训练时很难收敛。第三类方法通常是在传统轧制力模型结构的基础上给定一个或者多个待定参数，通过大量实际生产数据不断对待定参数进行自适应和自学习，适合于在线应用。但模型结构与平整轧制机理相差较大时，自适应后的物理参数可能会被无限的放大或缩小，失去了原有的物理意义。

从轧制力在线设定的角度而言，第三类方法是最为合适的，也是目前生产实际中主要采用的方法。从轧机设计、轧制规程制定的角度而言，第一类方法是最为合适的，但第一类方法的建模过程需要很强的专业知识，模型的推广应用受到限制。在第一类方法中，Roberts模型的全部公式都是显式的，使用十分方便。但Roberts模型的推导和验证是基于大延伸率(大于2%)干平整的，对于目前工业上常见的小延伸率平整，尤其是小延伸率湿平整，其计算精度无法满足要求。

综上所述，目前进行平整机设计与轧制规程制定时，仍然缺乏简单精确的轧制力模型。基于这一现状，本文综合考虑带材的弹性变形与塑性变形，基于非圆弧轧辊理论的大量计算结果，回归得到一套冷轧带钢平整机轧制力简化模型，可用于干平整或湿平整轧机设计、轧制规程制定。

1基本模型

平整轧制力为

(1)

式中，σs为变形抗力；B为带材宽度；L为变形区长度；x为坐标，变形区入口坐标为0，变形区出口坐标为L；Q(x)为应力状态系数，是x的函数。

(2)

1.1变形区长度

变形区长度基本回归方程如下：

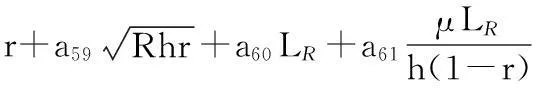
(3)

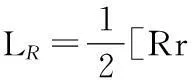
(4)

式中，a0～a61为回归系数；x1～x7分别为轧辊半径、摩擦因数、变形抗力、带材来料厚度、延伸率、入口张力与变形抗力比值，出口张力与变形抗力比值；R为轧辊原始半径；h为带材来料厚度；r为延伸率；μ为摩擦因数；LR为采用Roberts公式计算得到的变形区长度。

式(3)中，等号右边的前3项为7个输入参数二次多项式的完全形式，后5项是考虑到轧辊弹性变形机理并参考Roberts公式得到的特殊项。考虑到式(3)中的参数太多，实际使用非常不方便，为减少参数量，采用逐个减少参数的办法，将对相关系数影响很小的项逐个剔除，最终得到变形区长度的表达式：

L=b0+b1h+b2μ+b3r+b4σs+b5σ0/σs+

b6σ1/σs+b7Rσs+b8μσs+b9hr+b10h2

(5)

式中，b0～b10为回归系数；σ0、σ1分别为入口张应力与出口张应力。

式(5)的等号右边包含1个常数项、6个线性项和4个二次项，相较于式(3)，减少了51个参数，但对回归精度影响很小，复相关系数达到0.9887。回归得到的具体参数见表1，回归前后变形区长度对比如图1所示。由图1可知，回归式与原始数据吻合很好，对绝大部分样本而言，回归式与原始数据的相对误差为-10%～10%。

表1　变形区长度回归系数

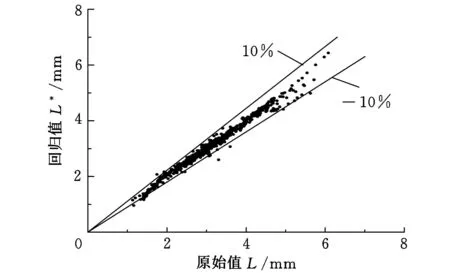
图1　变形区长度对比图

1.2平均应力状态系数

平均应力状态系数基本回归方程式如下：

(6)

式(6)中，等号右边的前3项与式(3)相同，后3项是参考Roberts公式得到的特殊项，需要注意的是，式(6)中的L为采用式(5)计算得到的变形区长度，而非式(4)计算得到的变形区长度。式(6)中参数同样太多，为减少参数量，仍然采用逐个减少参数的办法，将对相关系数影响很小的项逐个剔除，最终得到的应力状态系数的表达式为

(7)

式中，c0～c4为回归系数。

式(7)的等号右边包含1个常数项、2个线性项和2个特殊项，相较于式(6)，减少了55个参数，尽管回归系数很少，复相关系数仍然达到0.9632。回归得到的具体参数见表2，回归前后应力状态系数对比如图2所示。由图2可知，回归式与原始数据吻合很好，对绝大部分样本而言，回归式与原始数据的相对误差为-10%～10%。

表2　应力状态回归系数

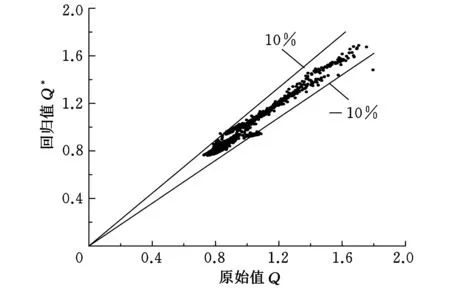
图2　应力状态系数对比图

2结果对比

采用式(5)与式(7)计算了4个典型算例，并将其与非圆弧轧辊理论的计算结果进行了对比，4个算例的计算参数与结果如表3、图3所示。表3中，L*、Q*分别为回归模型计算的变形区长与平均应力状态系数。由表3、图3可知，回归式计算的应力状态系数和变形区长度与原始值吻合较好。

表3　计算参数与结果

(a)例1

(b)例2

(c)例3

(d)例4 图3　变形区长度与应力状态综合计算结果

3模型分析

平整轧制时，轧制力随轧制速度变化非常显著，造成这一现象的主要原因有两个：一是变形抗力随着应变速度发生变化，二是摩擦因数随着轧制速度发生变化。文献[6]指出，随着轧制速度的增大，干平整的摩擦因数有增加的趋势；文献[10]指出，与普通冷轧类似，随着轧制速度的增加，湿平整的摩擦因数有降低的趋势。摩擦因数随轧制速度的定量变化规律，由于实际测量的困难，目前仍然没有一套成熟的理论，因此本文不作深入研究。

3.1变形抗力

关于变形抗力随应变速率的变化，文献[16]给出了一个使用比较广泛的表达式：

(8)

为考虑应变速率对变形抗力的影响，需要计算应变速率，其表达式可采用文献[6]的简化表达式：

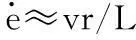
(9)

式中，v为轧制速度。

将式(5)与式(8)、式(9)综合考虑，发现变形区长度与变形抗力存在互为因果的关系，因此需要进行迭代计算。通过简单的理论分析可知，随着变形抗力的增加，变形区长度会增加；随着变形区长度的增加，应变速率变小，变形抗力变小，因此这一迭代过程从理论上说是绝对收敛的。

当考虑轧制速度对变形抗力影响时，采用本文模型计算轧制力的计算流程如图4所示。

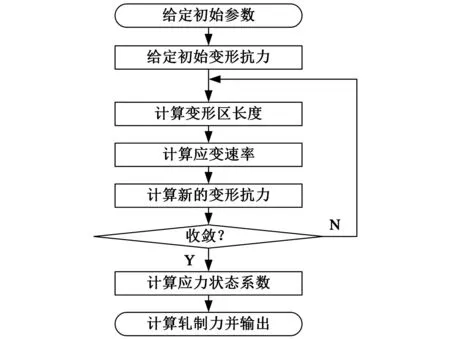
图4　轧制力计算流程图

3.2精度评估

由第2节可知，变形区长度与应力状态系数模型均存在一定程度的误差，同时，非圆弧轧辊理论本身也必然存在一定程度的误差，因此有必要通过实测数据对本文模型的精度进行评估。精度评估采用了两套平整机(900mm与1500mm平整机)的实测数据，其中，900mm轧机采用的平整模式为干平整，主要平整材料为Q195与Q215；1500mm轧机采用的平整模式为湿平整，主要平整原料为CQ、DQ与DDQ。对两套轧机的典型规格带材采用本文模型计算了轧制力，并与实测值进行了对比，结果见表4、表5。由表4、表5可知，对于典型规格产品，本文模型计算值与实测值偏差大部分在-15%～15%，少部分偏差超过20%。

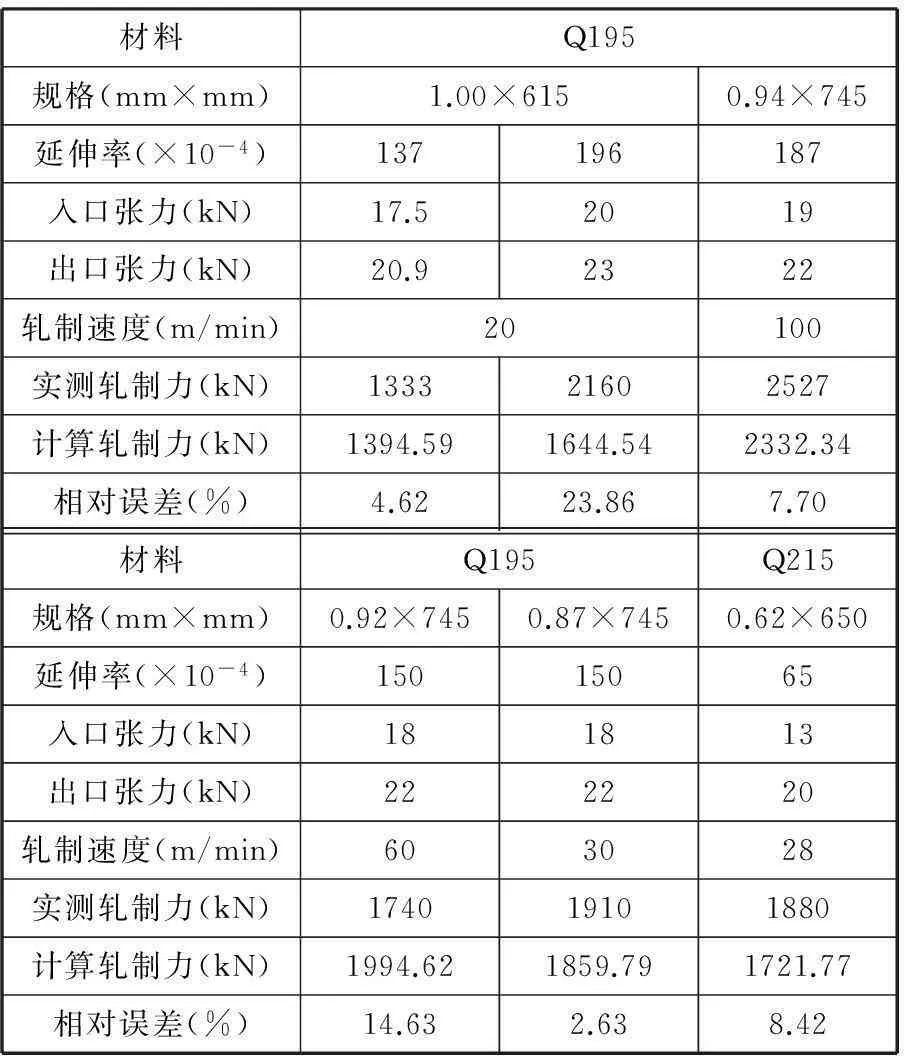
表4　900mm轧机轧制参数

表5　1500mm轧机轧制参数

4结论

(1)基于非圆弧轧辊理论，回归得到一套冷轧带钢平整机轧制力简化模型。该模型可用于干平整或湿平整轧机设计，轧制规程制定或轧制力在线设定。

(2)对于典型规格产品，本文模型计算值与实测值偏差大部分在-15%～15%，少部分偏差超过20%。

参考文献：

[1]白振华, 冯宪章, 蒋岳峰. 极薄带钢平整轧制过程辊型改造方案的研究[J]. 中国机械工程，2007，18(23)：2887-2889.

Bai Zhenhua，Feng Xianzhang，Jiang Yuefeng. Research on Reform Program of Roll Shape in Skin Rolling Process of Super Thin Strip[J]. China Mechanical Engineering，2007，18(23)：2887-2889.

[2]刘志亮，李文强，王英杰. 动态板形辊平整机板形控制机理模型研究[J]. 中国机械工程，2011，22(13)：1624-1628.

Liu Zhiliang，Li Wenqiang，Wang Yingjie. Research on Shape Control Model for DSR Skin Mill[J]. China Mechanical Engineering，2011，22(13)：1624-1628.

[3]于孟，张清东，李瑞，等. R2 级表面镀锡基板平整轧制过程表面粗糙度控制[J]. 钢铁，2010，45(12)：44-49.

Yu Meng，Zhang Qingdong，Li Rui，et al. Control of Surface Roughness for R2 Grade Tin Mill Black Plate in Two-stand Temper Mill Rolling[J]. Iron and Steel，2010，45(12)：44-49.

[4]李秀军, 白振华, 李亮亮, 等. 带钢平整轧制过程中色差综合控制技术的研究[J]. 钢铁，2009，44(11):60-63.

Li Xiujun，Bai Zhenhu，Li Liangliang，et al. Study of Color Aberration Combination Controlling Technique for Sheet Strip in Temper Rolling Processing[J]. Iron and Steel，2009，44(11):60-63.

[5]刘志亮，邱格君. 提高2030平整机预测精度的实用方法[J]. 钢铁，2006，41(7)：61-64.

Liu Zhiliang，Qiu Gejun. Practical Method of Precise Prediction on 2030 Skin Mill[J]. Iron and Steel，2006，41(7)：61-64.

[6]Roberts W L. 李裕华，译. 平整的近似理论[J]. 重型机械，1973(4)：41-59.

[7]连家创. 冷轧薄板轧制压力和极限最小厚度的计算(Ⅰ) [J]. 重型机械, 1979(2):20-37.

Lian Jiachuang. Calculation of Rolling Pressure and Minimum Rollable Thicknes for Cold-rolled Sheet[J]. Heavy Machinery，1979(2):20-37.

[8]白振华, 刘宏民, 李秀军, 等. 平整轧制工艺模型[M]. 北京: 冶金工业出版社，2010.

[9]Fleck N A，Johnson K L. Cold Rolling of Foil[J]. Proc. In-st. Mech. Eng., 1992, 206: 119-131.

[10]Domanti S A，Edwards W J. 箔材轧制模型在极薄带及平整轧制中的应用[C]//第六届国际轧钢会议译文集3. 北京：中国金属学会轧钢学会，1994：180-188．

[11]王东城, 彭艳, 刘宏民. 冷轧带钢平整机高精度高速度轧制力模型开发[J]. 塑性工程学报，2008，15(1)：172-177.

Wang Dongcheng，Peng Yan，Liu Hongmin. A High-resolution High-speed Rolling Force Model for Cold Strip Temper Rolling Mill[J]. Journal of Plasticity Engineering，2008，15(1)：172-177.

[12]杜凤山, 孙静娜, 李学通. 冷轧平整过程轧制压力分布非线性有限元研究[J]. 塑性工程学报，2008，15(3)： 186-190.

Du Fengshan，Sun Jingna，Li Xuetong. Finite Element Analysis of Normal Pressure Distributions in Temper Rolling[J]. Journal of Plasticity Engineering，2008，15(3)：186-190.

[13]魏立群, 卢冬华. 基于BP网络的平整轧制压力计算[J]. 钢铁，2002，37(12)：33-35.

Wei Liqun，Lu Donghua. BP Network Based Skin Rolling Force Calculation[J]. Iron and Steel, 2002,37 (12): 33-35.

[14]白振华, 康晓鹏, 龙瑞兵, 等. 工程实用平整轧制压力模型及其自学习技术研究[J]. 钢铁, 2008,43(10): 51-54.

Bai Zhenhua，Kang Xiaopeng，Long Ruibing，et al. Practical Temper Rolling Force Model and It’s Self Study Technology[J]. Iron and Steel, 2008,43(10): 51-54.

[15]薛栋梁, 王骏飞, 顾廷权, 等. 热镀锌机组平整机轧制力预设定模型研究[J]. 重型机械, 2010(6): 18-21.

Xue Dongliang，Wang Junfei，Gu Tingquan，et al. Study on Rolling Force Presetting Model for Skin Pass Mill in Hot Galvanizing Unit[J]. Heavy Machinery, 2010(6): 18-21.

[16]Roberts W L. 冷轧带钢生产[M]. 北京：冶金工业出版社，1985.

(编辑张洋)