基于RCSA的深孔内圆磨床主轴端点频响函数预测

基于RCSA的深孔内圆磨床主轴端点频响函数预测

李孝茹朱坚民张统超王健

上海理工大学，上海，200093

摘要：基于响应耦合子结构分析法预测了深孔内圆磨床主轴端点的频响函数。首先对磨床主轴进行子结构划分，计算各子结构自由状态下的频响函数矩阵，然后顺序刚性耦合各子结构的频响函数矩阵，对轴承支撑点使用结构修改法修改轴承约束下的已耦合子结构频响函数矩阵，直至耦合到最后一个子结构，得到主轴端点的频响函数。以某深孔内圆磨床为研究对象，分别基于该方法和有限元法，对其主轴端点的频响函数进行预测，并对其进行实验测试。实验及分析结果表明：该方法预测精度高于有限元分析方法预测精度、计算速度快，便于深孔内圆磨床主轴系统的结构优化。

关键词：深孔内圆磨床；主轴端点；频响函数预测；响应耦合子结构分析；结构修改法

中图分类号：TH113；TG581.2

收稿日期：2015-04-28

基金项目：国家自然科学基金资助项目(50975179)；上海市教委科研创新项目(11ZZ136)；上海市科委科研计划资助项目(13160502500)；沪江基金资助项目(D14005)

作者简介：李孝茹，女，1980年生。上海理工大学机械工程学院博士研究生。主要研究方向为精密检测、机床动力学等。朱坚民(通信作者)，男，1968年生。上海理工大学机械工程学院教授、博士研究生导师。张统超，男，1990年生。上海理工大学机械工程学院硕士研究生。王健，男，1989年生。上海理工大学机械工程学院硕士研究生。

Frequency Response Prediction of Deep Hole Internal Grinder Spindle

Endpoint Based on Receptance Coupling Substructure Analysis

Li XiaoruZhu JianminZhang TongchaoWang Jian

University of Shanghai for Science and Technology，Shanghai，200093

Abstract：Based on RCSA, this paper predicted the frequency response function of the endpoint of a deep hole internal grinder spindle. At first, the method separated the model of grinder spindle into several subsections to calculate their free-state frequency response function (FRF) matrices, then rigidly coupled the FRF matrices of each substructure sequentially, revised the FRF matrices of the coupled substructure with structural modification method at the support points of bearings, coupled till to the last substructure, then the FRF of the endpoint of grinder spindle was calculated．With a deep hole internal grinder spindle system as the research object, the paper predicted the FRF of the spindle endpoint through proposed method and finite element method, meanwhile a group of FRF data were collected by experiments．Experimental results indicate that this method, with higher prediction precision and faster calculation speed, is better in the structure optimization of the deep hole internal grinder spindle system.

Key words：deep hole internal grinder; spindle endpoint; frequency response characteristic prediction; receptance coupling substructure analysis(RCSA); structural modification method

0引言

深孔内圆磨床主轴系统的动态特性是磨床整机动态性能的重要组成部分，主轴端点的频响函数是主轴系统动态特性的直接反映，对磨床的磨削稳定性、极限磨削速度、加工精度、可靠性和寿命等有显著影响[1-2]。深孔内圆磨床主轴由于长径比大、支撑刚性差等原因，其端点的动态性能往往低于其他类型磨床并容易产生磨削颤振。因此在深孔内圆磨床主轴系统的设计阶段，准确、快速地预测其端点的频响函数，对于主轴结构及其参数的优化设计具有重要意义。

目前，有限元法是预测磨床主轴端点频响函数的主要方法。文献[3]运用ANSYS对超高速磨床主轴系统进行了建模和动力学分析，对其固有频率、振型和临界转速进行了预测；文献[4]考虑轴承刚度参数和螺栓联结结合面参数，建立了某高速外圆磨床电主轴系统的有限元模型，通过理论模态分析了主轴系统的固有频率和模态振型，并通过实验模态测试验证了有限元分析结果的正确性；文献[5]在ANSYS中建立了某轧辊数控磨床主轴系统的有限元模型，通过模态分析和谐响应分析得到了主轴系统的频响函数。以上研究使用有限元法预测磨床主轴系统的频响函数时，有限元法建模过程复杂、计算效率低，且模型一旦建立则不便在其结构参数的优化中动态修改，故难以用于深孔内圆磨床主轴系统的结构优化。

响应耦合子结构分析(receptance coupling substructure analysis，RCSA)是铣刀刀尖点频响函数预测的最有效方法，它将铣床主轴系统划分为若干子结构(各子结构的频响函数矩阵可通过梁模型简化理论计算、有限元模型计算或实验模态测试等方法获得)，再通过响应耦合各子结构频响函数矩阵预测出刀尖点的频响函数[6-8]。由于该方法预测精度高、计算简单，国内外学者对其进行了大量研究[9-11]。深孔内圆磨床主轴长径比大，其几何结构和铣床主轴-刀柄-铣刀系统类似，都可视为多段梁结构耦合而成，因此可基于RCSA预测其端点的频响函数。本文据此提出了基于RCSA的深孔内圆磨床主轴端点频响函数预测新方法，以某深孔内圆磨床为研究对象，基于本文方法和有限元法分别对其主轴端点的频响函数进行预测和实验测试，得到了预期的结果。

1深孔内圆磨床主轴端点频响函数预测原理

1.1主轴系统各子结构自由状态下的响应耦合分析

深孔内圆磨床主轴系统的典型结构如图1所示，细长的主轴安装在壳体中，主轴左端、右端分别由一组面对面安装的角接触轴承支撑。砂轮安装在主轴的左端点O1(O1为砂轮安装点，O2为皮带轮安装点)处，主轴在该点的频响函数反映了整个主轴系统的动态特性，与机床的磨削精度、速度和稳定性直接关联，本文研究此端点处频响函数的预测方法。

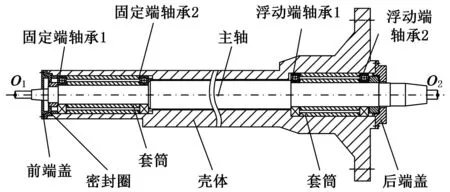
图1　深孔内圆磨床主轴系统的典型结构

图1中，深孔内圆磨床主轴由多段均匀圆柱梁和两段梯形圆柱梁结构组成，可将其按照圆柱梁的段数划分为相同数目的子结构，即子结构A～子结构K，如图2所示。

图2　深孔内圆磨床主轴系统子结构划分

圆柱梁子结构的频响函数矩阵直接由梁模型计算得到。为了计算梯形圆柱梁子结构的频响函数矩阵，可根据等质量法将其简化为等直径圆柱梁。图2中，假设梯形圆柱梁B两端圆截面的直径分别为d1和d2，则其等效的等直径圆柱梁直径为

(1)

通过这种简化后，主轴的每个子结构均为等直径圆柱梁。下面以图2中两圆柱梁A和B为例，说明主轴系统子结构之间的耦合过程。

如图3所示，子结构A和子结构B响应耦合构成子结构A-B。考虑平动和转动两个自由度，子结构A的频响函数矩阵表示为

(2)

式中，Hij、Lij、Nij和Pij分别为位移/力、位移/力矩、转角/力以及转角/力矩的频响函数，i，j=A1，A2；xi、θi分别为子结构A在i点的位移和转角响应；fj、mj分别为施加在子结构A在j点的作用力和作用力矩。

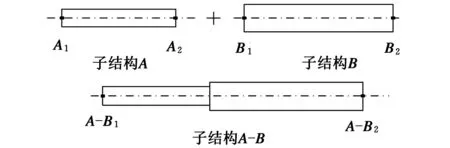
图3　响应耦合子结构分析法原理图

子结构A的频响函数矩阵Aij(i=j时为原点频响函数，i≠j时为跨点频响函数)可统一表示为

(3)

式(3)中，每个子矩阵Aij包含对应点的频响函数，例如梁A的A1点频响函数矩阵为

(4)

同理，子结构B的频响函数矩阵可表示为

(5)

对于由子结构A和B刚性耦合而成的子结构A-B，设其频响函数矩阵为

(6)

则子结构A-B的频响函数矩阵与子结构A、B的频响函数矩阵之间的关系为[12]

C11=A11-A12(A22+B11)-1A21

(7)

C12=A12(A22+B11)-1B12

(8)

C21=B21(A22+B11)-1A21

(9)

C22=B22-B21(A22+B11)-1B12

(10)

由式(7)～式(10)可知，耦合后子结构的频响函数矩阵可通过各子结构频响函数矩阵的数学运算得到。将图2中的子结构A～子结构K按顺序刚性耦合，即子结构A与子结构B耦合构成的结构AB，再与子结构C耦合，构成ABC，…，直至耦合到子结构K，可得到主轴在自由状态下其端点的频响函数。

1.2主轴系统各子结构频响函数计算

子结构A～子结构K在自由状态下各自的频响函数矩阵可通过EB梁模型或Timoshenko梁模型计算得到[13-14]。EB梁模型计算简单、可靠，适用于细长梁的频响函数计算，但文献[15-16]的研究表明：EB梁模型假设梁只产生弯曲变形，忽略了转动惯量和剪切变形，当梁的长径比较小时，EB梁的计算频响函数误差较大。Timoshenko梁模型考虑横向剪切变形的影响，对于长径比较小的梁，Timoshenko梁的计算频响函数具有较高的计算精度。尽管深孔内圆磨床主轴的整体结构长径比较大，但划分子结构后各子结构长径比较小，因此本文基于Timoshenko梁模型计算主轴各子结构的频响函数[17]。两端自由的Timoshenko梁的特征方程为

(11)

D11=(α-λ)(cosα-coshβ)

(12)

(13)

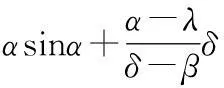
(14)

D22=λα(coshβ-coshα)

(15)

(16)

(17)

(18)

式中，ρ、E、G分别为梁材料的密度、弹性模量和剪切模量；A、I、L分别为梁的截面积、截面惯性矩和长度；k′为梁的剪切系数，k′=6(1+υ)/(7+6υ)；υ为梁材料的泊松比。

根据特征方程(式(11))，可以获得梁的r阶弹性模态以及相应模态的量纲一频率参数αr、βr，并由此确定梁的平动振型函数：

(19)

同理可得梁的转动振型函数:

(20)

(21)

(22)

根据振型函数的正交性可得

(23)

令r=s=1, 2, …,n，可求出常数Ar。

(24)

(25)

以圆柱梁的左截面中心为坐标原点，梁轴线方向为x轴，建立图4所示的坐标系。

图4　两端自由的Timoshenko梁坐标定义

图4中，两端自由的Timoshenko梁模型的频响函数为

(26)

(27)

(28)

(29)

j,k=1,2

将式(19)、式(24)和式(25)代入式(26)～式(29)，j=k=1，可得图4中端点1的原点频响函数：

(30)

(31)

(32)

(33)

同理，当j=1，k=2时，可得端点1的跨点频响函数；当j=k=2时，可得端点2的原点频响函数；当j=2，k=1时可得端点2的跨点频响函数。

1.3主轴在轴承支撑下各子结构频响函数矩阵的耦合

以上通过RCSA得到深孔内圆磨床主轴自由状态下其端点的频响函数。实际的磨床主轴由前后4个轴承支撑(如图1所示)，并且轴承的支撑刚度对主轴端点的频响函数有较大的影响，因此必须考虑轴承的支撑约束，建立轴承支撑下的主轴端点的频响函数。

本文考虑轴承的刚度和阻尼对主轴系统动态特性的影响，使用结构修改法[18]建立轴承支撑下的主轴端点频响函数预测模型。将轴承对主轴的支撑简化为若干个平动和转动弹簧-阻尼单元，根据结构修改法对主轴阶梯梁重新进行子结构划分，如图5所示，图中，U为转动弹簧-阻尼单元，V为平动弹簧-阻尼单元。

图5　具有轴承支撑的主轴系统子结构划分

图6所示为图5中子结构A～D耦合成子结构R后，再引入轴承约束U、V，通过修改子结构R的频响函数矩阵确定新的子结构R′频响函数矩阵的原理。

图6　结构修改法耦合原理

图6中，假设子结构R的质量矩阵、刚度矩阵及阻尼矩阵分别为M、K和C，在简谐力F的作用下子结构R的位移和转角响应为

x=(K-ω2M+iωC)-1F

(34)

子结构R的频响函数矩阵可以表示为

α=(K-ω2M+iωC)-1

(35)

假设子结构R′的频响函数矩阵为

ξ=[(K+ΔK)-ω2(M+ΔM)+iω(C+ΔC)]-1

(36)

式中，ΔM、ΔK、ΔC分别为子结构R的质量、刚度和阻尼的变化量。

式(35)、式(36)两边求逆得

ξ-1=α-1+D

(37)

D=ΔK-ω2ΔM+iωΔC

(38)

式中，D为动态结构修改矩阵。

式(37)的两边左乘α、右乘ξ可得

α=ξ+αDξ

(39)

由式(39)解得修改后的频响函数矩阵：

ξ=(I+αD)-1α

(40)

(41)

(42)

式中，ky、kθ、cy、cθ分别为轴承的径向刚度、转动刚度、径向阻尼和转动阻尼的动态结构修改参数。

根据式(7)～式(10)，依次将子结构A～D偶合成子结构R，将子结构R的频响函数矩阵记为

(43)

修改频响函数矩阵P中的元素排列顺序为[18]

(44)

则子结构R′的频响函数矩阵为

αP′=(I+αPD)-1αP

(45)

式中，I为单位矩阵。

对图5所示的磨床主轴系统，首先对主轴进行子结构划分，按照式(26)～式(29)确定各子结构的频响函数矩阵；根据式(7)～式(10)将各子结构顺序刚性耦合，耦合过程中，遇到轴承支撑时，把对应轴承参数Ky和Kθ代入式(41)，将式(41)、子结构R频响函数矩阵元素重排后的新矩阵(式(44))及单位矩阵I代入式(45)，可得到轴承约束下的耦合子结构频响函数矩阵，然后按照同样方法，继续根据式(7)～式(10)与其余各子结构顺序刚性耦合，最后得到整个主轴端点的频响函数矩阵，确定主轴砂轮安装点的位移/力频响函数H11。

2主轴端点频响函数预测实例

2.1本文方法预测

图7　磨床主轴测试实物图

以图7所示的某深孔内圆磨床为研究对象，应用本文方法对其主轴端点的频响函数进行预测。

首先对该磨床主轴进行子结构划分，根据主轴系统的结构特征划分成子结构A～子结构L，如图5所示。子结构B和子结构K是梯形圆柱梁，其梯度比较小，分别为0.1°和0.144°，可以根据式(1)将其简化为等直径圆柱梁，简化后各子结构的几何尺寸如表1所示。

表1　主轴各子结构的几何尺寸

主轴的材料为钢，其密度ρ=7800kg/m3，弹性模量E=200GPa，泊松比υ=0.3，阻尼因子γ=0.003。主轴固定端支撑轴承的径向刚度为880MN/m，浮动端支撑轴承的径向刚度为520MN/m，角接触轴承具有自动调节功能，其转动刚度和阻尼均为0。

根据本文方法得到磨床主轴砂轮安装点的频响函数矩阵，其中位移/力频响函数的实部和虚部如图8所示。

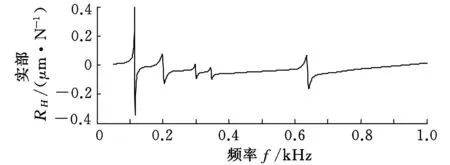
(a)实频特性曲线

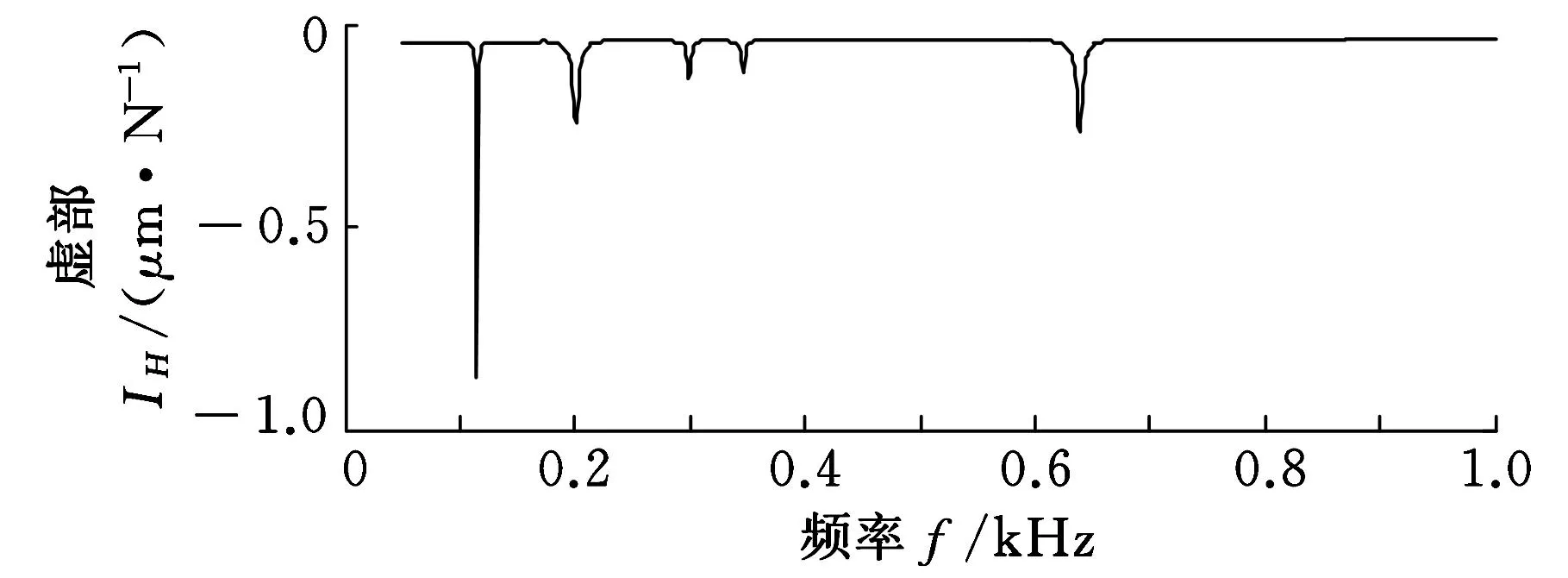
(b)虚频特性曲线 图8　本文方法预测的主轴端点频响函数曲线

2.2有限元法预测

2.2.1主轴系统有限元模型的建立

为了与本文方法预测结果进行对比，使用有限元法对磨床主轴左端点处的频响函数进行预测。在SolidWorks软件中建立主轴系统的实体模型，导入HyperMesh软件中建立主轴系统的有限元模型。

(1)实体模型简化。为了使有限元网格划分生成的单元形状合理，提高计算分析的精度和效率，在建立有限元模型前，对实体模型作以下简化：对模型中的倒角、倒圆均作直线化处理；忽略主轴两端的联结螺纹，以等直径圆柱梁代替；忽略有限元计算结果影响小的壳体、套筒、端盖等零件。

(2)网格化分。整个模型的单元类型均选择ANSYS中的Solid95实体单元(20节点六面体单元，具有较高的计算精度)。在HyperMesh软件中通过体分割进行网格划分，共划分约35.5万个Solid95单元。

(3)轴承结合部建模。轴承结合部的刚度是影响主轴系统有限元计算结果正确性的关键因素。采用ANSYS软件提供的自定义MATRIX27刚度单元，忽略轴承阻尼对固有频率的微小影响，根据轴承刚度模拟结合部的接触特性。将轴承内圈固定在主轴上，使用MPC184单元将轴承内外圈分别刚性耦合到2个独立的节点上，再使用2个刚度单元将2个节点在轴向、径向分别联结，建立的轴承结合部模型如图9所示，主轴系统轴承的固定端径向刚度为880MN/m，浮动端径向刚度为520MN/m。

图9　轴承结合部的建模

(4)边界条件。根据主轴系统的实际约束情况，对所有轴承外圈表面的节点施加了全约束。

2.2.2主轴系统理论模态分析

考虑材料阻尼因子，在ANSYS中使用QRDamped法进行模态求解，获得主轴系统前6阶模态振型和固有频率，分别如图10和表2所示。

(a)第1阶模态振型

(b)第2阶模态振型

(c)第3阶模态振型

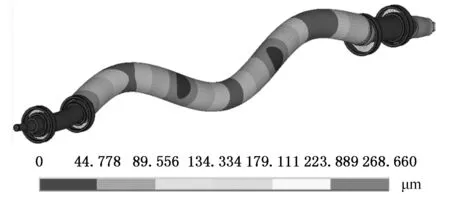
(d)第4阶模态振型

(e)第5阶模态振型

(f)第6阶模态振型 图10　主轴系统前6阶模态振型

本文方法(Hz)有限元法(Hz)实测(Hz)本文方法误差(%)有限元法误差(%)1115108.3113.11.74.22206181.2197.64.38.33299-293.71.8-4347325342.61.35.15--561.9--66416456341.11.77-947.9926-2.4

由图10可知，主轴系统第1阶模态振型为1阶弯曲振动，第2阶模态振型为扭转振动，第3阶模态振型为2阶弯曲振动，第4阶模态振型为3阶弯曲振动，第5阶模态振型为主轴右端弯曲振动，第6阶模态振型为4阶弯曲振动。

2.2.3主轴系统谐响应分析

为了获得主轴端点的频响函数，对主轴系统进行谐响应分析。在主轴端点沿Z向(竖直向下)施加作用力Fz=1N，在ANSYS中使用Modalsuperposition法进行谐响应分析，并提取主轴端点Z方向的位移Dz，经过计算得到主轴端点的频响函数曲线，如图11所示。

(a)实频特性曲线

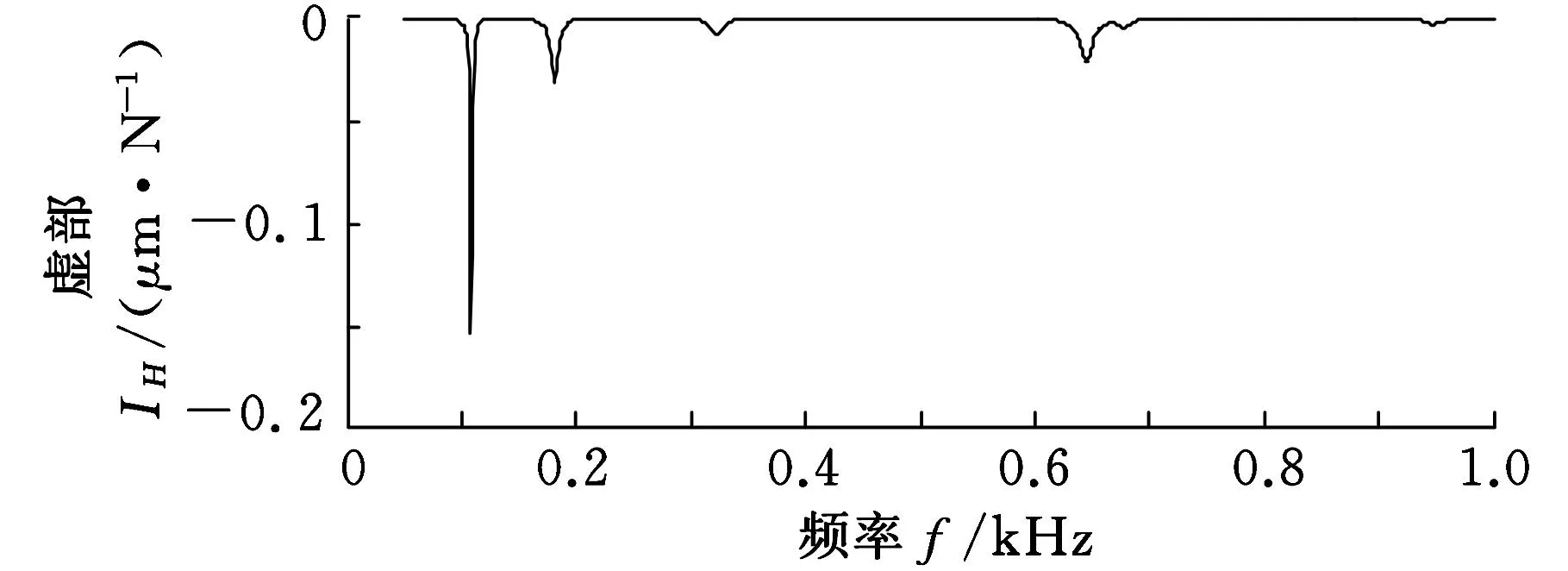
(b)虚频特性曲线 图11　有限元法预测的主轴端点频响函数曲线

3实验研究

3.1实验模态测试

为了验证本文方法和有限元法预测结果的正确性，使用锤击法对磨床主轴砂轮安装点进行模态测试，获得其实测频响函数。实验中使用Kistler9724A型激振力锤对主轴砂轮安装点施加激励力，使用BK4525B型三向加速度传感器拾取主轴端点振动信号，通过搭载NI-9234动态信号采集模块的NIcDAQ-9172数据采集系统对激励力以及主轴端点的加速度信号进行同步采集，使用ModalVIEW模态分析软件进行模态分析，模态测试原理如图12所示。

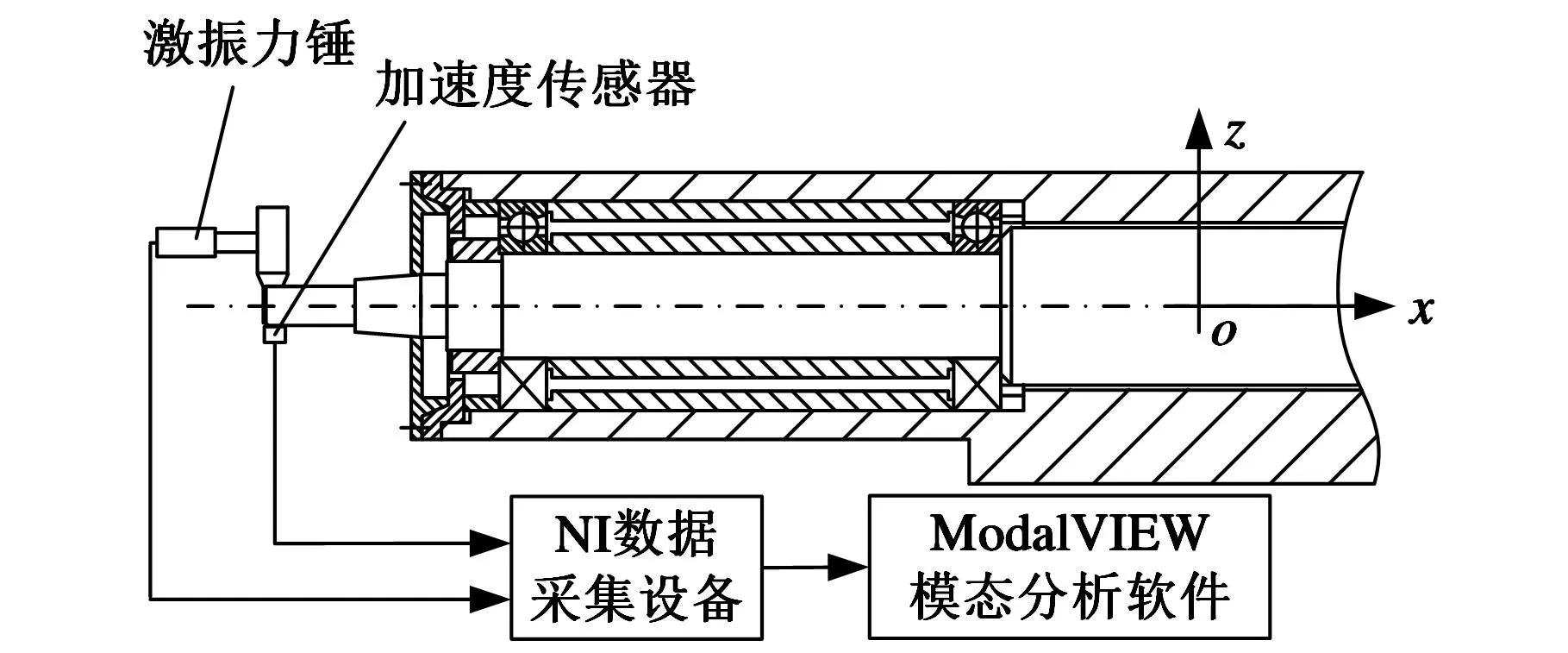
图12　实验模态测试原理图

在ModalVIEW软件中通过最小二乘复频率法对实测加速度频响函数进行曲线拟合和模态参数识别。为了便于与前述预测频响函数进行对比，根据HD(ω)=-HA(ωw)/ω2将实验模态测试得到的加速度频响函数转换为位移频响函数，其中，HA(ω)、HD(ω)分别为磨床主轴砂轮安装点处的加速度频响函数、位移频响函数。最终得到的主轴端点实测位移频响函数曲线，如图13所示。

(a)实频特性曲线

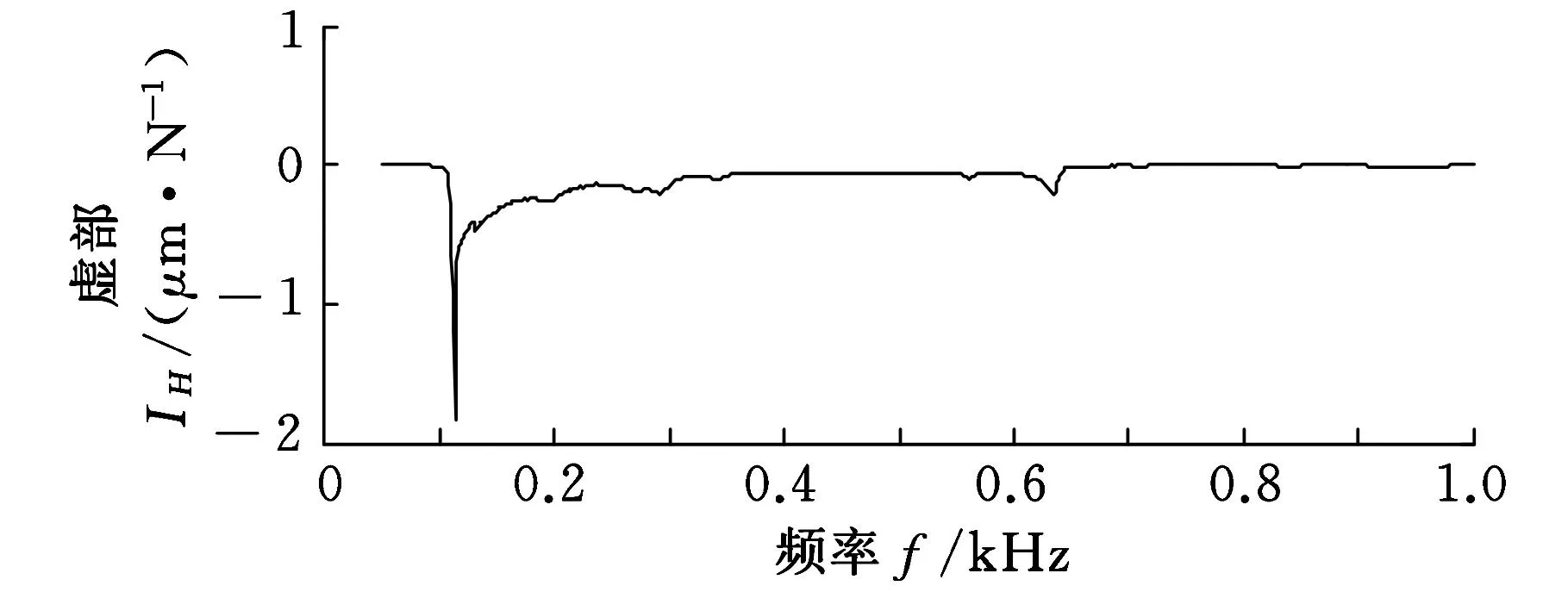
(b)虚频特性曲线 图13　实测的主轴端点频响函数曲线

3.2结果分析

将本文方法得到的预测频响函数曲线、有限元法得到的预测频响函数曲线与实测的频响函数曲线放在同一个图中进行对比，如图14所示。

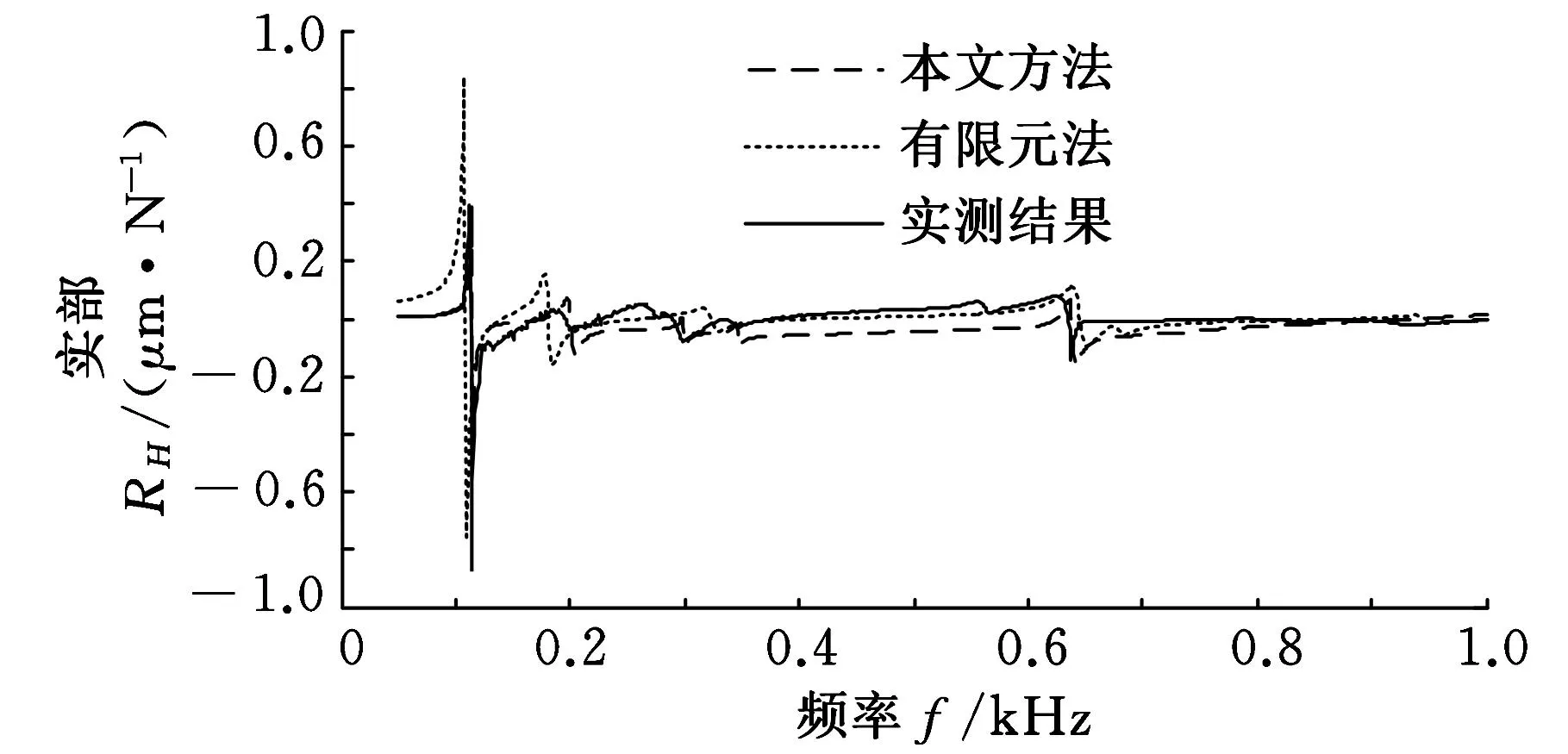
(a)实频特性曲线

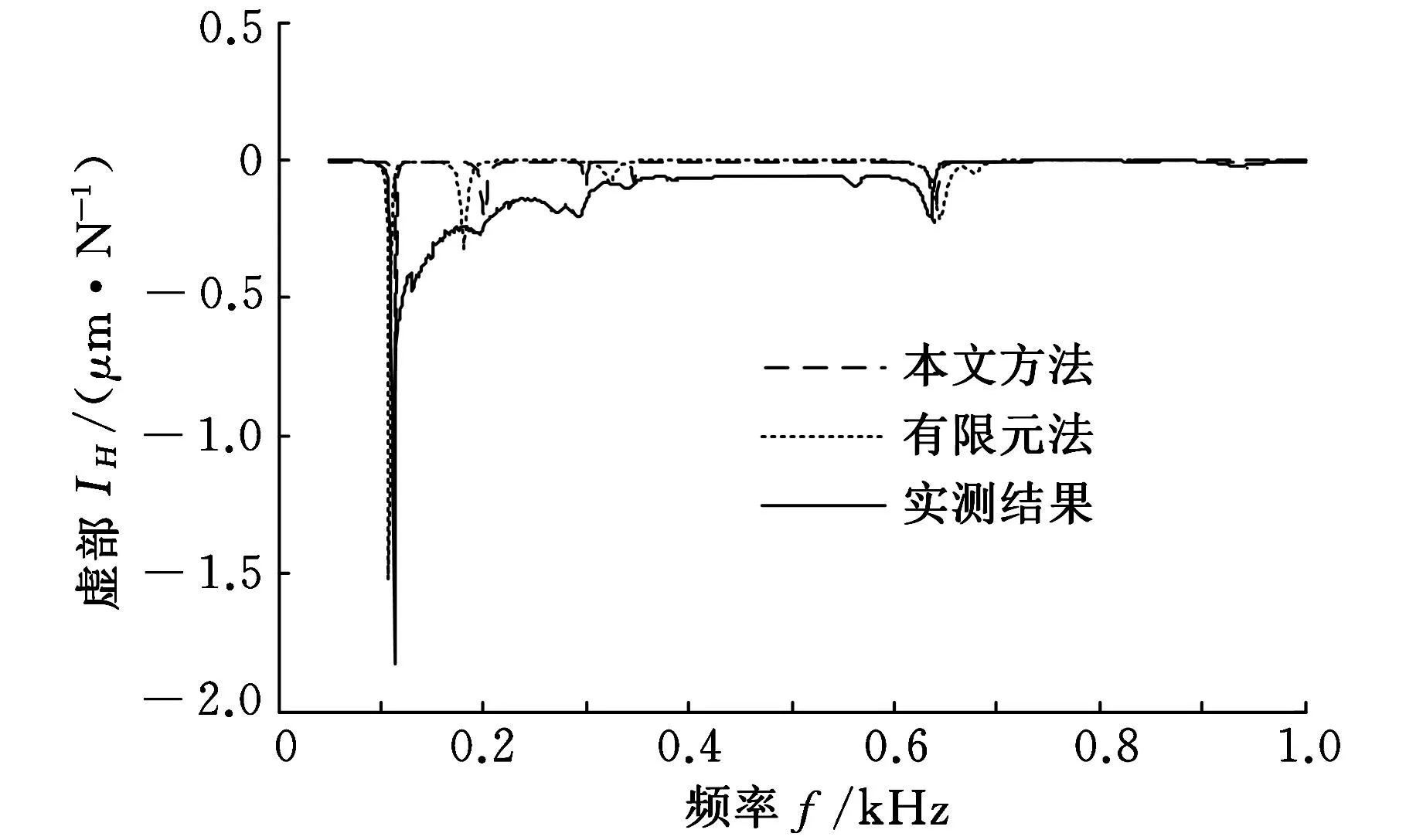
(b)虚频特性曲线 图14　主轴端点的预测、实测频响函数对比

从图14a可以看出，本文方法、有限元法和实测得到的实频特性曲线整体上一致。在第1阶固有频率处，本文方法获得的频响函数比有限元法获得的频响函数更加接近实测结果。在其余几阶固有频率处，有限元法得到的频响函数比本文方法得到的频响函数更接近实测频响函数。实际磨削加工过程中，主轴系统的第1阶固有频率对加工性能的影响最大，而其余几阶固有频率对加工性能的影响相对较小。从图14b可以看出，本文方法和有限元法得到的虚频特性曲线也比较接近，但是均与实测虚频特性曲线有一定的差异，引起这种差异的主要原因是本文实测得到的是加速度频响曲线，为了与有限元法和本文方法预测的位移频响曲线进行对比，需要对加速度频响函数进行两次积分，正是两次积分中的积分误差导致了实测结果与预测结果的偏差。

为了进一步分析本文方法预测的频响函数的准确性，比较本文方法、有限元法和实测频响函数的前7阶固有频率。从表2可知，本文方法和有限元法得到的频响函数均存在模态丢失，如本文方法得到的固有频率丢失了第五、第七阶模态。由于实际磨削加工往往重点关注前三阶固有频率，故可忽略本文方法中的模态丢失。有限元法得到的频响函数丢失了第三、第五阶模态。本文方法确定的固有频率和实测固有频率最大相对误差为4.3%，有限元法和实测得到的固有频率最大相对误差为8.3%。

综上所述，可认为本文方法确定的预测频响函数比有限元法更接近实测频响函数。

此外，本文使用ANSYS13.0对磨床主轴左端点处的频响函数(0～1000Hz，频率间隔0.5Hz)进行计算，计算工作站使用Intel(R)Xeon(R)CPU，2个处理器(每个处理器具有6核)的主频都是2.93GHz，内存48GB，计算所用时间大约为4min。在相同的计算条件下，运用本文方法计算磨床主轴左端点处的频响函数耗时不到30s。可以看出，本文方法的计算效率较高。

另外，有限元法采用的是数值计算方法，为非解析方法，只能利用数值计算得到预测结果。本文方法推导了频响函数的解析解，可在任意结构参数下直接利用相关公式计算频响函数，且计算简单，结构参数易于修改，便于深孔内圆磨床主轴的改进设计和动态性能优化。

4轴承刚度对主轴端点动态特性的影响

轴承支撑作为主轴的重要边界条件，其径向刚度是影响磨床主轴端点动态特性的关键因素之一。基于本文方法建立的深孔内圆磨床主轴端点频响函数预测模型可以方便地分析出轴承刚度对主轴端点频响函数的影响。由于轴承阻尼很小且不影响固有频率，故本文只研究轴承刚度的变化对主轴端点动态特性的影响。

4.1固定端轴承径向刚度的影响

根据上文可知，深孔内圆磨床主轴系统主要由固定端和浮动端两处轴承支撑，首先研究固定端轴承径向刚度对主轴端点动态特性的影响。保持浮动端轴承的径向刚度kyr=5.2×108N/m不变，固定端轴承径向刚度分别在原刚度kyf=1.76×109N/m基础上增加50%和减小50%，即取2.64×109N/m和8.8×108N/m，轴承径向刚度变化前后预测的频响函数曲线如图15所示。

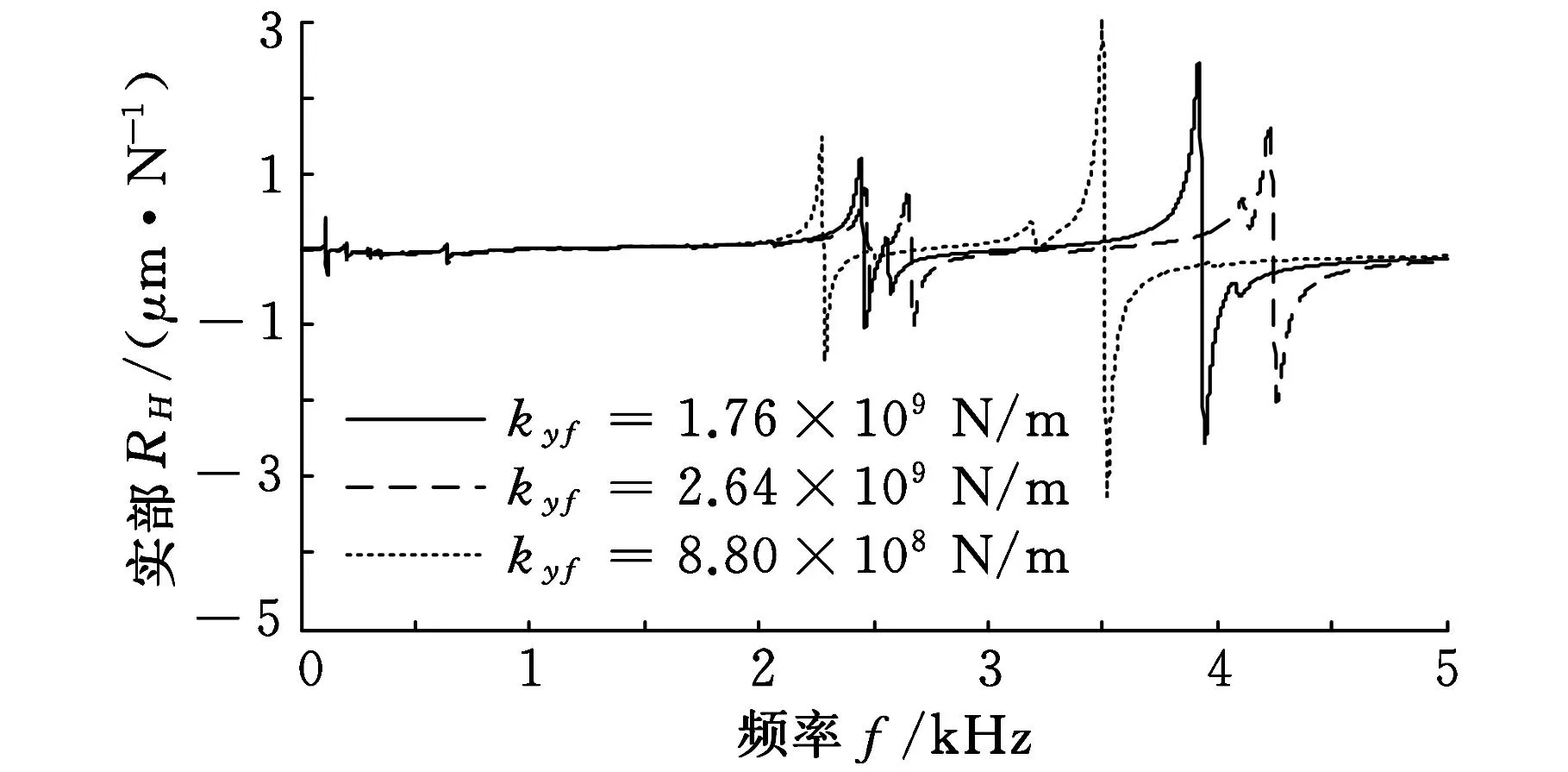
(a)实频特性曲线

(b)虚频特性曲线 图15　固定端轴承径向刚度对主轴端点频响影响

由图15可知，在轴承径向刚度增大50%时，系统前三阶固有频率分别增加了0、0.5%和0.7%。随着模态阶次的增加，轴承径向刚度对固有频率的影响逐渐增大；前三阶固有频率处的实部幅值分别减小10%、增加7%、增加7%，且随着模态阶次的增加，其实部幅值先减小后增大。第1阶固有频率处的实部幅值随轴承径向刚度的增加而明显减小，因此提高固定端轴承的径向刚度有利于提高机床的磨削稳定性。当轴承径向刚度减小到原轴承径向刚度的50%时，固有频率及其实部幅值与刚度增大时的变化趋势相反。

4.2浮动端轴承径向刚度的影响

保持固定端轴承径向刚度kyf=1.76×109N/m不变，浮动端轴承径向刚度在原刚度kyr=5.2×108N/m基础上分别增加50%和减小50%，即取7.8×108N/m和2.6×108N/m，轴承径向刚度变化前后预测的频响函数对比如图16所示。

(a)实频特性曲线

(b)虚频特性曲线 图16　浮动端轴承径向刚度对主轴端点频响影响

由图16可知，随着主轴浮动端轴承径向刚度的增大，系统前三阶固有频率分别减小3%、3.5%和3%。相对固定端轴承，浮动端轴承刚度对固有频率的影响较大。第一阶固有频率处实部幅值减小5%，第二、第三阶固有频率处幅值基本没有变化。因此，浮动端轴承径向刚度的增加会减小系统第一阶固有频率，不利于机床磨削稳定性的提高。

5结论

(1)提出了一种基于RCSA的深孔内圆磨床主轴端点频响函数的预测新方法。该方法首先根据磨床主轴的结构进行子结构划分，并基于Timoshenko梁模型计算各子结构的频响函数矩阵；然后使用结构修改法引入轴承的刚度；最后将各子结构进行刚性耦合，得出主轴端点的频响函数。

(2)以某深孔内圆磨床为研究对象，基于本文方法、有限元法分别对主轴端点的频响函数进行了预测，并与实测结果进行对比分析。结果表明：本文方法得到的预测频响函数曲线与实测频响函数曲线总体趋势一致，与有限元法相比，本文方法更加接近实测频响函数曲线，且可在任意结构参数下直接利用公式得到频响函数，计算更加简单快速。

(3)基于本文方法预测模型分析了轴承径向刚度对主轴端点频响特性的影响，分析结果表明：固定端轴承径向刚度对主轴端点的固有频率影响较小，对频响函数的幅值影响较大；浮动端轴承径向刚度对主轴端点的固有频率影响较大，对频响函数的幅值影响较小。

参考文献：

[1]胡如夫，孙庆鸿，陈南，等．高精度内圆磨床结构动态优化设计研究[J]．中国机械工程，2002，13(18)：1542-1544.

HuRufu，SunQinghong，ChenNan，etal．ResearchonStructureDynamicOptimizationDesignofHigh-precisionofInternalGrinder[J].ChinaMechanicalEngineering，2002，13(18)：1542-1544.

[2]周晓玲，汪中厚，陈琪华，等．基于Pro/MECHANICA的深孔内圆磨床内圆磨具的精确建模及模态分析[J]. 制造业信息化，2006(1)：42-44.

ZhouXiaoling，WangZhonghou，ChenQihua，etal．AccurateModelingandModalAnalysisofDeepHoleGrindingToolsBasedonPro/MECHANICA[J]．JournalofManufacturingAutomation,2006(1)：42-44.

[3]于天彪，王学智，关鹏，等．超高速磨削机床主轴系统模态分析[J]．机械工程学报，2012，48(17)：183-188.

YuTianbiao，WangXuezhi，GuanPeng，etal．ModalAnalysisofUltra-high-speedGrindingSpindle[J]．JournalofMechanicalEngineering，2012，48(17)：183-188.

[4]刘杰，李蓓智，杨建国，等．高速外圆磨床电主轴系统的有限元建模和动态性能分析[J]．东华大学学报，2012，38(5)：542-545.

LiuJie，LiBeizhi，YangJianguo，etal．FEMModelingandDynamicPerformanceAnalysisofElectricSpindleSystemofHighSpeedCylinderGrindingMachine[J]．JournalofDonghuaUniversity，2012，38(5)：542-545.

[5]中国机械工程学会设备与维修工程分会．设备状态监测与故障诊断技术及其工程应用[M]．北京：机械工业出版社，2010．

[6]FilizS，ChengCH，PowellKB，etal．AnImprovedToolHolderModelforRCSATool-pointFrequencyResponsePrediction[J]．PrecisionEngineering，2009，33(1)：26-36.

[7]MovahhedyMR，GeramiJM．PredictionofSpindleDynamicsinMillingbySub-structureCoupling[J].InternationalJournalofMachineToolsandManufacture，2006，46(3/4)：243-251.

[8]SchmitzTL，DuncanGScot．Three-componentReceptanceCouplingSubstructureAnalysisforToolPointDynamicsPrediction[J].JournalofManufacturingScienceandEngineering，2005，127(4)：781-790.

[9]柴银刚，孟德浩，龙新华，等．高速主轴-夹具-刀具系统动态特性分析[J]．噪声与振动控制，2013，33(6)：25-30．

CaiYingang，MengDehao，LongXinhua，etal．AnalysisofDynamicCharacteristicsofHighSpeedSpindle-holder-toolSystem[J].NoiseandVibrationControl，2013，33(6)：25-30.

[10]WangEr-hua，WuBo，HuYou-min，etal．DynamicParameterIdentificationofTool-spindleInterfaceBasedonRCSAandParticleSwarmOptimization[J]．ShockandVibration，2013，20(1)：69-78.

[11]NamaziM，AltintasY，AbeT，etal．ModelingandIdentificationofToolHolder-spindleInterfaceDynamics[J]．InternationalJournalofMachineToolsandManufacture，2007，47(9)：1333-1341.

[12]ErtürkA，BudakE，ÖzgüvenHN．AnalyticalModelingofSpindle-toolDynamicsonMachineToolsUsingTimoshenkoBeamModelandReceptanceCouplingforthePredictionofToolPointFRF[J]．InternationalJournalofMachineToolsandManufacture，2006，46(15)：1901-1912.

[13]LeeJ，SchultzWW．EigenvalueAnalysisofTimoshenkoBeamsandAxisymmetricMindlinPlatesbythePseudospectralMethod[J]．JournalofSoundandVibration，2004，269 (3/5)：609-621.

[14]GeistB，McLaughlinJR．AsymptoticFormulasfortheEigenvaluesoftheTimoshenkoBeam[J]．JournalofMathematicalAnalysisandApplications，2001，253(2)：341-380.

[15]KivancEB，BudakE．StructuralModelingofEndMillsforFormErrorandStabilityAnalysis[J]．InternationalJournalofMachineToolsandManufacture，2004，44(11)：1151-1161.

[16]SchmitzTL，DaviesMA，KennedyMD．ToolPointFrequencyResponsePredictionforHigh-speedMachiningbyRCSA[J].JournalofManufacturingScienceandEngineering，2001，123 (4)：700-707.

[17]Aristizabal-OchoaJD．TimoshenkoBeam-columnwithGeneralizedEndConditionsandNonclassicalModesofVibrationofShearBeams[J].JournalofEngineeringMechanics，2004，130 (10)：1151-1159.

[18]ÖzgüvenHN．StructuralModificationsUsingFrequencyResponseFunctions[J]．MechanicalSystemsandSignalProcessing，1990，4 (1)：53-63.

(编辑张洋)