有限长轴承支撑的转子系统非线性动力学分析

有限长轴承支撑的转子系统非线性动力学分析

黑棣1,2吕延军2张永芳2

1.陕西铁路工程职业技术学院，渭南，7140002.西安理工大学，西安，710048

摘要：基于π油膜假设，运用变分约束原理和分离变量法求得了有限长动压轴承非线性油膜力的近似解析表达式。通过计算比较可知，该方法和有限元法的计算结果非常接近，而且可以节约大量计算时间。在此基础上，以转子的角速度、圆盘处的偏心量及转轴的刚度为控制参数，运用Newmark法分析了轴承-转子系统的非线性动力学行为。数值结果揭示系统具有周期运动、倍周期运动、准周期运动、六周期运动、十周期运动等复杂丰富的非线性动力学特征。

关键词：非线性动力学；轴承-转子系统；有限长轴承；稳定性；分岔

中图分类号：TH133

收稿日期：2015-01-04

基金项目：国家自然科学基金资助项目(51375380)；陕西铁路工程职业技术学院常规项目(2013-19)

作者简介：黑棣，男，1983年生。陕西铁路工程职业技术学院机电系讲师，西安理工大学机械与精密仪器工程学院博士研究生。主要研究方向为非线性动力学及控制、润滑理论及新型轴承技术。发表论文10余篇。吕延军，男，1972年生。西安理工大学机械与精密仪器工程学院教授、博士研究生导师。张永芳，女，1975年生。西安理工大学印刷与包装工程学院副教授。

Analysis of Nonlinear Dynamics of Rotor System Supported by Finite Long Bearing

Hei Di1,2Lü Yanjun2Zhang Yongfang2

1.Shaanxi Railway Institute, Weinan，Shaanxi，714000

2.Xi’an University of Technology，Xi’an，710048

Abstract:Based on the assumption of π oil film, an approximation expression of nonlinear oil film force of finite hydrodynamic bearing was obtained by variational constraint principal and the separation of variables. The results calculated by the proposed method are in good agreement with the oil film forces by the finite element method, and the computing cost is reduced greatly. Based on the nonlinear oil film force, the speed of rotor, eccentricity of disk and stiffness of shaft were taken as control parameters, nonlinear dynamic behaviors of bearing-rotor system were analyzed by Newmark method. Numerical results reveal periodic, double-periodic, quasi-periodic, 6-periodic, 10-periodic of rich and complex nonlinear behaviors of the system.

Key words: nonlinear dynamics；bearing-rotor system；finite long bearing；stability；bifurcation

0引言

大型旋转机械广泛用于燃气轮机、航空发动机、工业压缩机及各种电动机等机械装置中，是国家基础设施和基础工业中最关键、最核心的设备之一，在电力、航空、冶金、石化、纺织、机械、动力、运输等行业中有着举足轻重的地位。轴承-转子系统是旋转机械的核心部件，且在高速、精密旋转机械中的应用日益广泛，所以对轴承-转子系统非线性动力学特性的研究十分重要。

轴承-转子系统的非线性动力学行为和稳定性的研究主要是基于无限短轴承模型[1-6]和无限长轴承模型[7-10]。当轴承的长径比非常小的时候(无限短轴承假设)，油膜力沿轴承周向的分布就可以忽略。相反，当轴承的长径比非常大的时候(无限长轴承假设)，油膜力沿轴承轴向的分布也可以忽略。

无限短和无限长轴承模型是非常简单的模型，并不能反映实际的情况。为了更准确地计算油膜力，学者们提出了许多计算油膜力的方法。Zheng等[11]提出了一个里兹模型来计算油膜力，这种方法可以节约大量的计算时间。Xiao等[12]基于变分不等式理论提出了一个快速有效的计算油膜力的算法，此算法将油膜力及其Jacobis的计算转化为求解一组线性代数方程。基于多参数法，Vignolo等[13]给出了无限长轴承假设下油膜力的近似解析解，并运用此方法求得了静态油膜力。Hirani等[14]、Bastani等[15]运用不同的无限短和无限长轴承模型的组合来近似求解有限长轴承油膜力。Wang等[16]基于动态π油膜假设得到了有限长轴承油膜力的解析解。

本文运用变分原理和分离变量法求得了有限长轴承油膜力的近似解析解，即在求解雷诺方程的时候，将雷诺方程中的压力分布函数看作是2个独立函数的乘积(一个函数仅仅是轴承周向坐标的函数，另一个函数仅仅是轴承轴向坐标的函数)。在求得有限长轴承油膜力的近似解析解之后，针对柔性对称转子，分析了此轴承-转子系统的非线性动力学行为。

1转子系统的动力学方程

有限长滑动轴承支撑的对称柔性转子模型如图1所示。

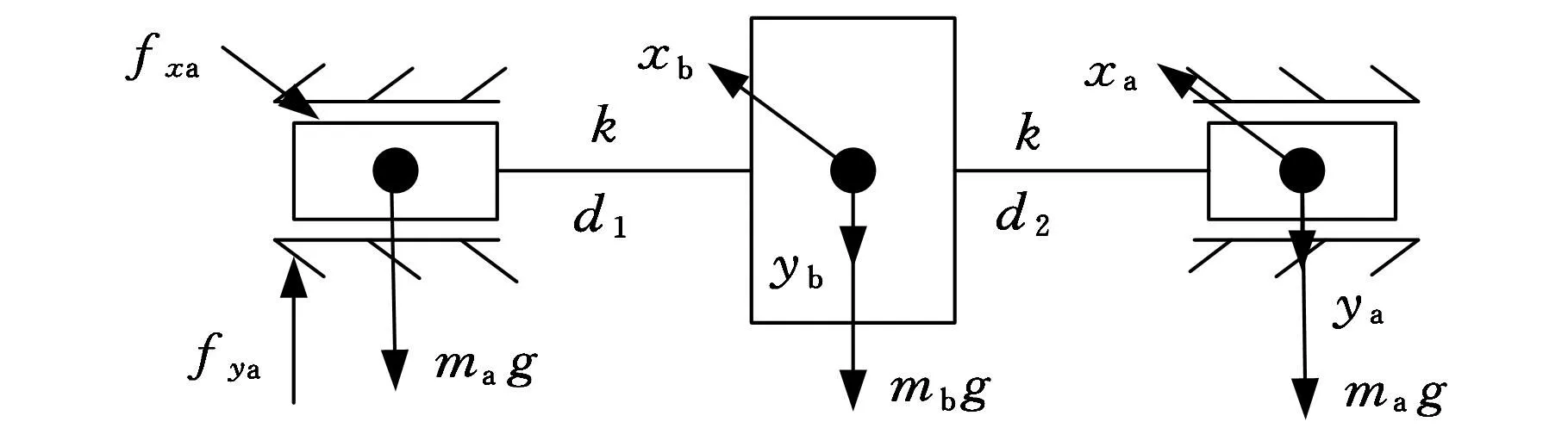
图1　有限长滑动轴承—柔性转子系统示意图

有限长滑动轴承支承的对称柔性转子系统动力学方程可写为

(1)

2ma+mb=m

式中，M、K分别为转子的质量矩阵和刚度矩阵；f为轴承的非线性油膜力；Q为施加在转子上的周期激励力(与角速度同步的不平衡激励或气动力激励)；x为转子的位移；m为转子总质量；ma、mb分别为集中到2个轴颈及圆盘处的质量；E、I分别为转子的弹性模量及转子截面的赤道惯性矩；l为两个轴承的中心距；ω为转子角速度；g为重力加速度；eji(i=x，y；j=a，b)为轴承及圆盘处不平衡质量偏心距在x、y方向的分量；fxa、fya分别为2个轴承在x轴和y轴负方向的非线性油膜力分量。

对于轴承-转子系统，为了理论推导和计算方便，引入如下量纲一变量：

式中，X、Y分别为轴颈中心x、y方向的位移分量；e为偏心量；c为轴承半径间隙；m′为转子质量的一半；σ为Sommerfeld数(Sommerfeld数是表征系统载荷的参数)；B为轴承宽度；η为润滑油动力黏度；R为轴承半径。

为了研究方便，引入系统参数：

该参数对于具体的轴承-转子系统，是一个常量。

2有限长轴承的油膜力计算

2.1油膜力的计算方法

图2给出了有限长动压轴承示意图及其计算坐标。图2中，Ob为轴承中心，Oj为轴颈中心，Φ为从y轴负方向顺时针转至油膜位置的角度，θ为偏位角，φ为从OjOb延长线顺时针方向转至油膜位置的角度，fr、ft分别为作用在轴颈上的非线性油膜力径向和切向分量，fx、fy分别为作用在轴颈上的非线性油膜力在x轴和y轴负方向的分量，h为油膜厚度，r为轴颈半径，W为轴承载荷。

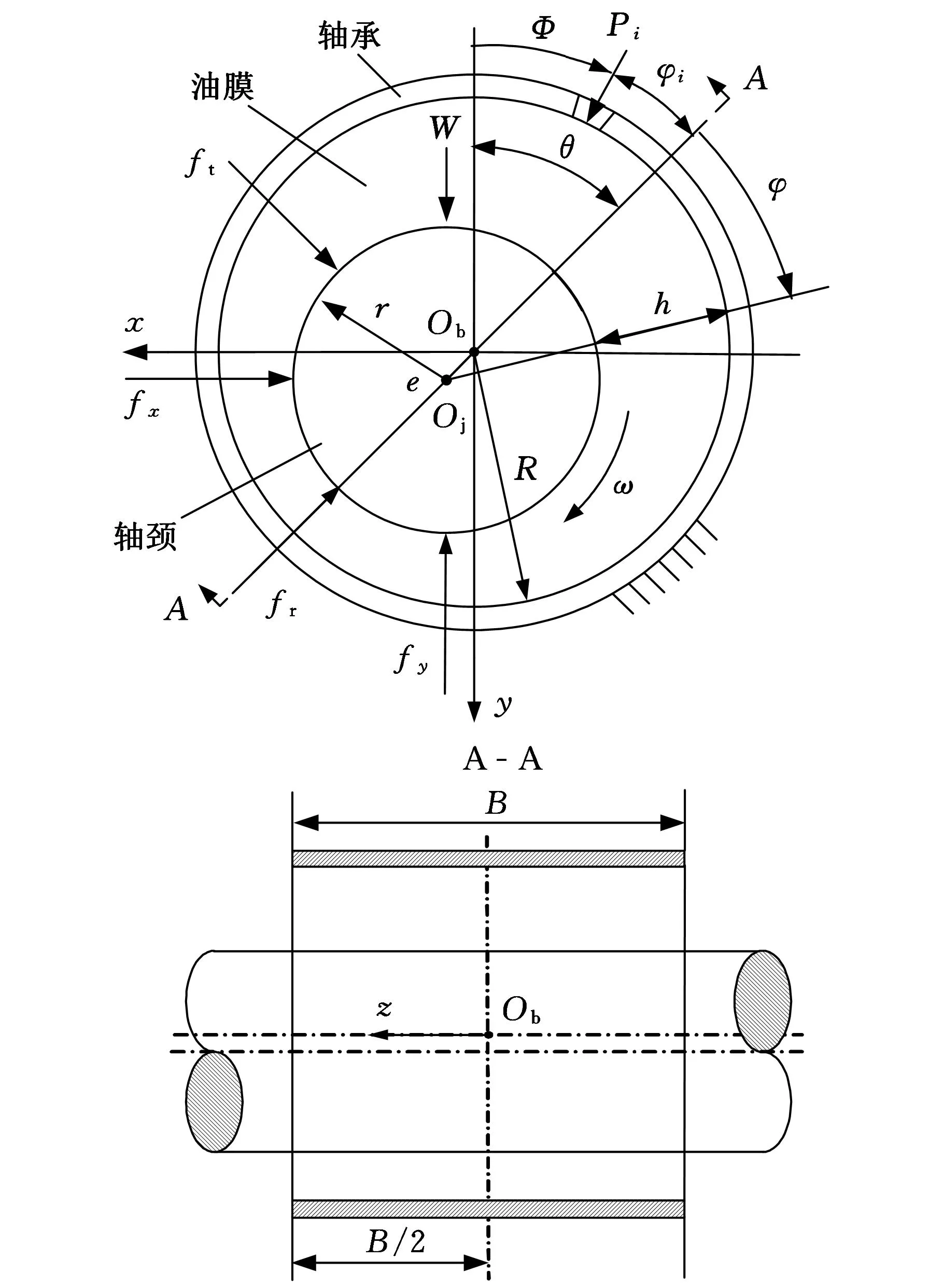
图2　有限长轴承图

对于径向滑动轴承，将润滑油膜视为不可压缩的流体，则其一般的Reynolds方程为

(2)

h=c+αcosφ

式中，Gφ、Gz为紊流因子；p为油膜的压力；γ为轴承周向坐标；z为轴承轴向坐标；U为轴颈的周向速度；α为偏心距。

引入以下量纲一变量：

λ=2z/Bε=α/cτ=ωtP=p/p0

p0=2ωη/ψ2H=1+εcosφ

式中，λ为量纲一轴向坐标；τ为量纲一时间；H为量纲一油膜厚度；ε为偏心率；ψ为间隙比；P为量纲一的油膜压力。

将式(2)代入式(1)可得

(3)

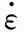
本文基于π油膜假设，运用变分原理和分离变量法对式(3)进行求解，求得非线性油膜压力分布的近似解析解。求解过程中，所用到的边界条件：油膜起始边处的油膜压力为0，即φ=0，P=0；油膜终止边处的油膜压力为0，即φ=π，P=0；油膜在终止边处连续，即φ=π，∂P/∂φ=0。

为了表达方便，将式(3)改写为

E(P)=f

(4)

式(4)定义在平面(φ，λ)的有界区域Ω上，边界为Γ，设H1(Ω)是Soblev空间，B(u，v)：H1(Ω)×H1(Ω)→R是强制对称连续双线性泛函，其中

(5)

u,v∈H1(Ω)

f(v)是H1(Ω)上的线性连续泛函：

f(v)=∬ΩfvdΩ

(6)

定义二次泛函：

J(v)=B(u，v)/2-f(v)

(7)

根据润滑力学第一变分原理，如果P是式(4)的解，那么P也同时满足如下泛函的极值问题：

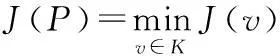
(8)

其中，检验函数集K是H1(Ω)中的非空闭凸集。

油膜压力只存在于油膜收敛区，则式(8)只在0≤φ≤π和-1≤λ≤1范围内成立。假设非线性油膜压力试验函数是2个独立函数的乘积即P(φ，λ)=P*(φ)ζ(λ)，其中，P*(φ)是关于φ的未知函数，ζ(λ)是λ的未知函数。要想求得油膜压力试验函数P(φ，λ)，则需分别求解2个独立函数P*(φ)和ζ(λ)。

将试验函数P(φ，λ)=P*(φ)ζ(λ)代入式(7)可得

(9)

对式(9)取一阶变分，由极值条件得

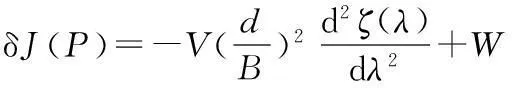
(10)

由于P*(φ)符合一阶变分条件，故有W=-K，则式(10)可写为

(11)

由式(11)即可求解出

(12)

通过以上方法可以求出独立函数ζ(λ)的表达式，由于非线性油膜压力试验函数P(φ，λ)=P*(φ)ζ(λ)，所以要想得到油膜压力试验函数P(φ，λ)的表达式，则还需求出独立函数P*(φ)的表达式。基于无限长轴承假设，P*(φ)的表达式可以通过以下的方法求出。

无限长轴承是基于轴承宽度B远大于轴承直径d这个假设，即B≫d。当B≫d时，油膜力沿轴向的变化率较其沿周向的变化率可以忽略不计(∂p/∂z≪∂p/∂φ)，即λ方向的压力梯度可忽略，也就是说无限长轴承的油膜压力函数仅仅是关于轴承周向坐标φ的函数。由于P*(φ)也仅仅是关于轴承周向坐标φ的函数，所以可以将无限长轴承油膜压力分布函数作为P*(φ)。

基于无限长轴承假设，式(3)可以写为

(13)

对式(13)积分两次，即可求得

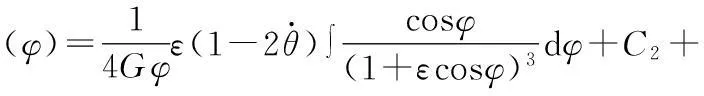
(14)

通过对P(φ，λ)积分，我们可以求出径向、切向的量纲一油膜力Fr和Ft：

(15)

由Fr、Ft可以求出x、y方向的油膜力分量Fx和Fy：

(16)

2.2油膜力的计算结果

2.1节提出了求解有限长轴承油膜力近似解析解的方法，为了验证此方法的可行性，将本文提出方法的计算结果、无限长轴承模型的计算结果和FEM计算结果进行比较。对比参数如下：偏心率ε=0.5，x、y方向速度分别为vx=0.01，vy=0，有限长滑动轴承宽径比B/d=1.0。图3给出了3种方法的计算结果。

(a)三种方法计算的F x

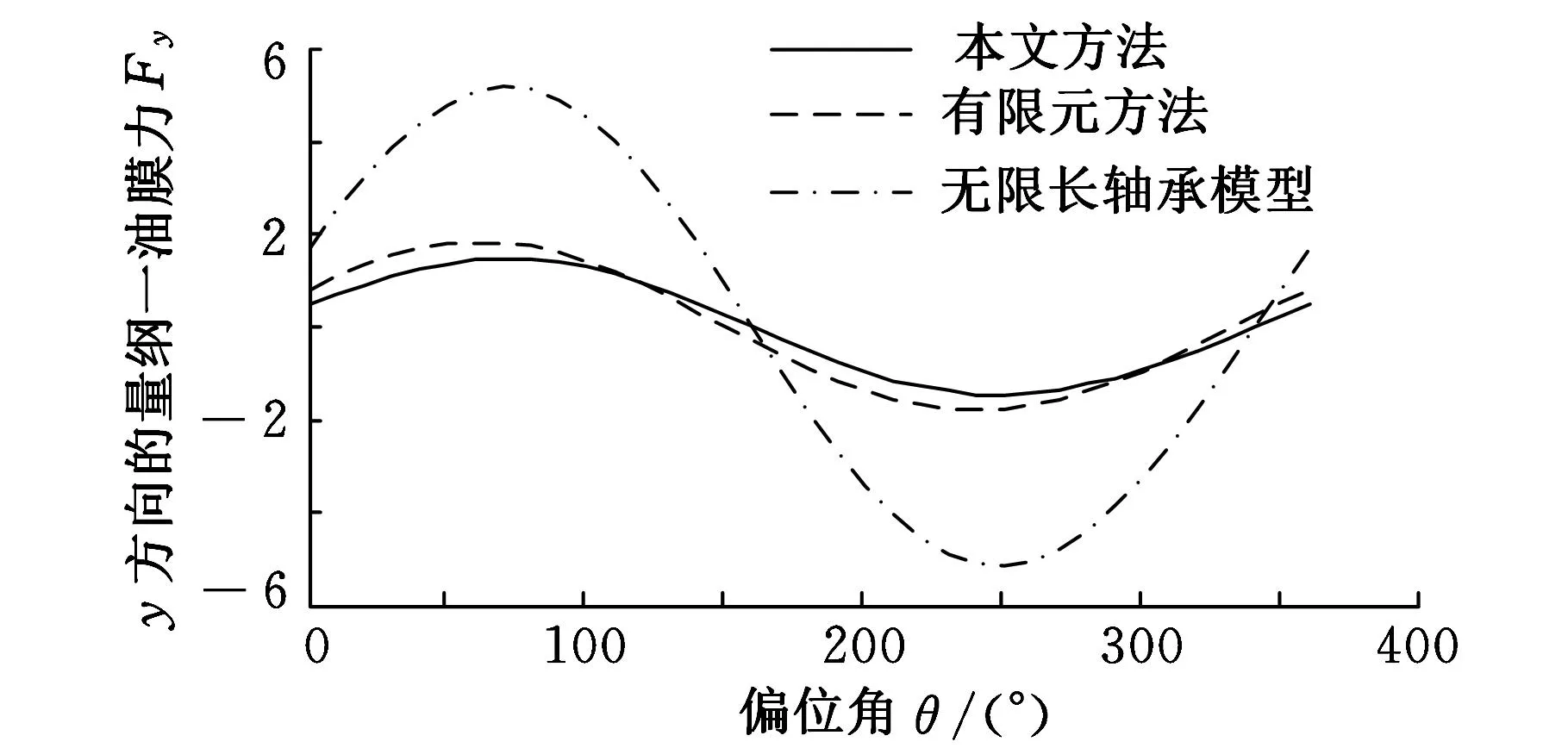
(b)三种方法计算的F y 图3　三种方法计算的油膜力的比较

从图3可以看出，本文提出方法的计算结果与FEM的计算结果吻合得非常好，无限长轴承模型计算的结果与FEM的计算结果相差较大。

图4给出了本文提出方法的计算速度和FEM的计算速度。从图4可以看出，本文提出方法的计算速度远高于FEM的计算速度，即本文提出的方法可以节约大量的计算时间。

图4　本文方法与FEM方法的计算速度

3数值算例

3.1以量纲一角速度为控制参数

(a)轴承处

(b)圆盘处 图5　不同转速下转子轴承处和圆盘处y方向的分岔图

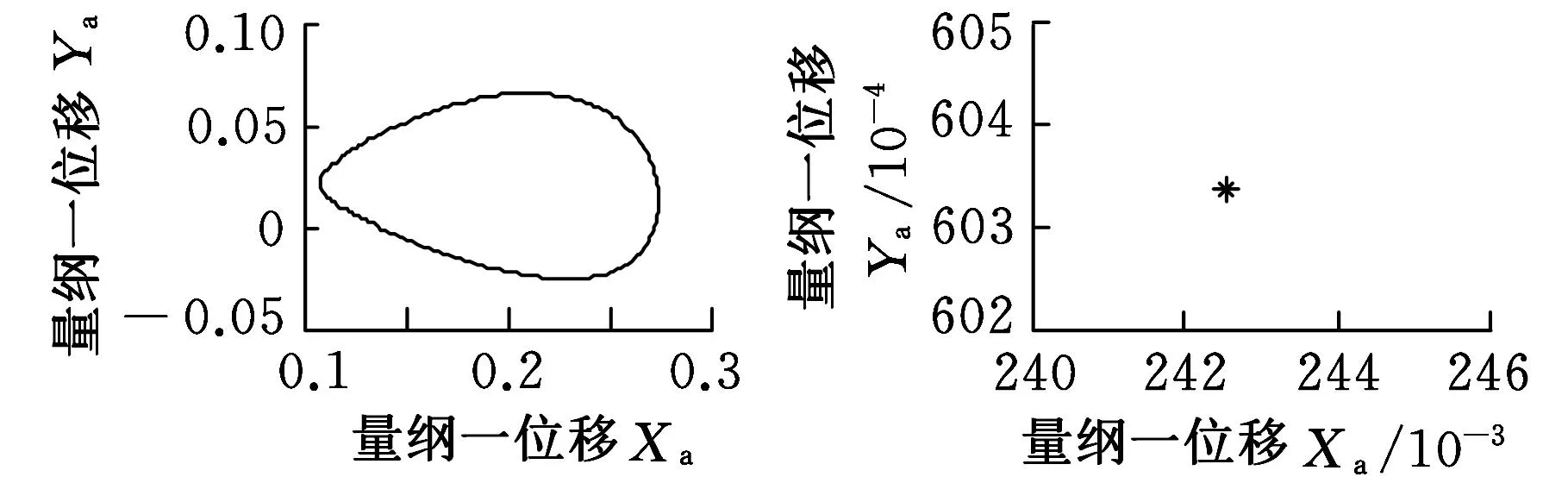
(a)周期轨迹(b)Poincaré映射点列 图6　转子轴承处的周期轨迹和 Poincaré映射点列( =0.95)

(a)准周期轨迹

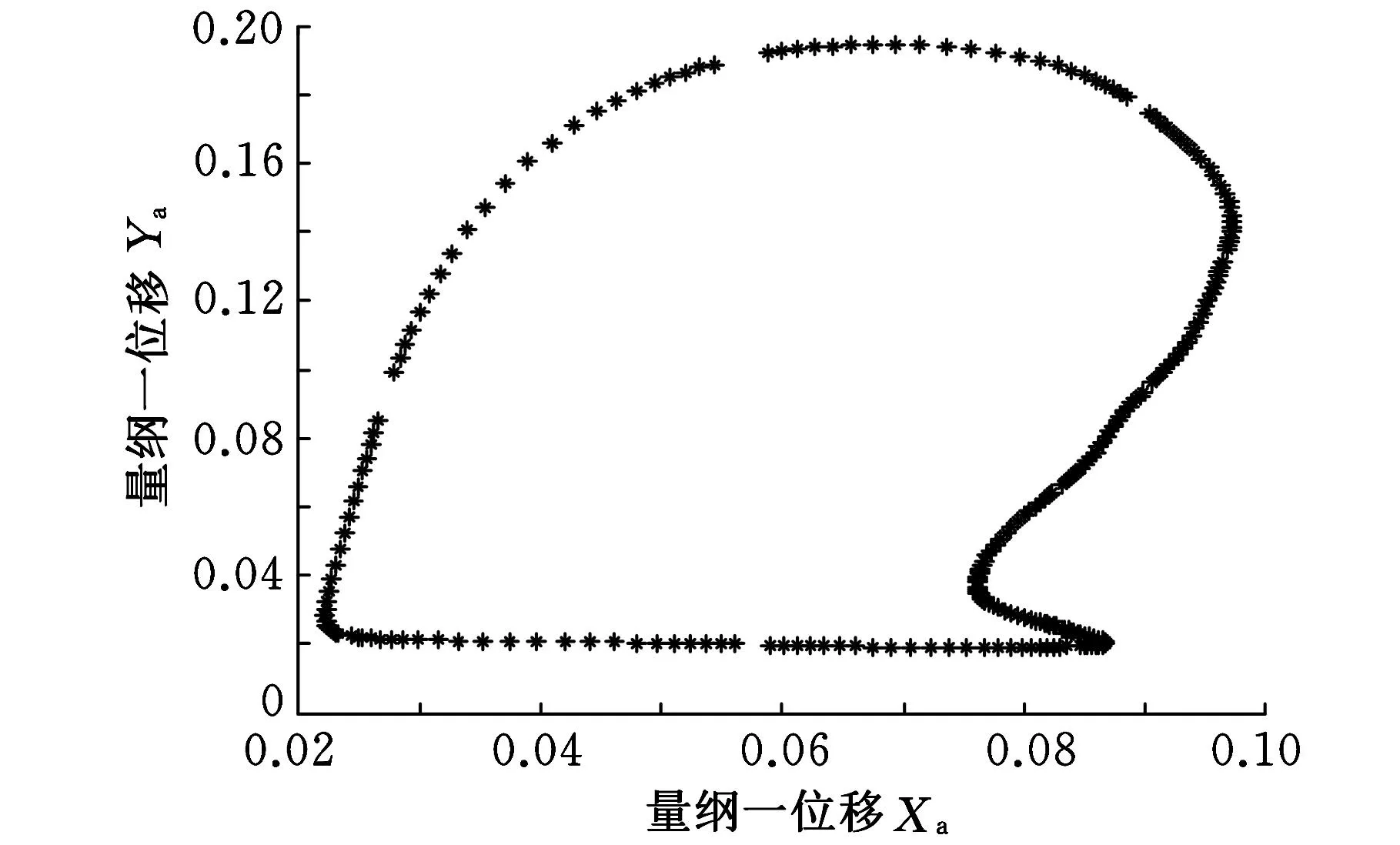
(b)Poincaré映射点列 图7　转子轴承处的准周期轨迹和 Poincaré映射点列( =1.05)

(a)十周期轨迹

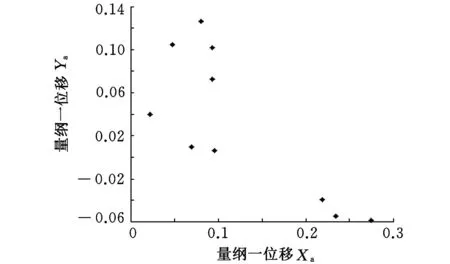
(b)Poincaré映射点列 图8　转子轴承处的十周期轨迹和 Poincaré映射点列( =1.10)

3.2以转轴量纲一刚度为控制参数

图9为轴承处和圆盘处转子中心y方向的位移随转轴量纲一刚度变化的分岔图。由图9可以看出，转子的运动非常复杂，当转轴的量纲一刚度从2变化到6时，转子所经历的运动分别为周期运动、准周期运动、周期运动、倍周期运动。由此可以看出，刚度对转子系统的运动影响较大。图10所示为转轴的量纲一刚度k=2.5时，转子轴承处转子的运动轨迹和Poincaré映射点列。随着转轴刚度的增加，系统将发生拟周期分岔。图11为k=3.7时，转子轴承处准周运动轨迹、Poincaré映射图。随着转轴刚度继续增加，系统将发生倒分岔，即由准周期运动变为周期运动。当转轴刚度再继续增加，系统将会发生倍周期分岔，即由原来的周期运动转化为倍周期运动。图12为k=5.2时，轴承处转子的倍周期运动轨迹、Poincaré映射图。从图12b可以看出，倍周期轨迹在穿越Pioncaré截面时为2个不动点。转轴的刚度继续增加，系统将再次发生倒分岔，即由原来的倍周期运动变为周期运动。

(a)轴承处

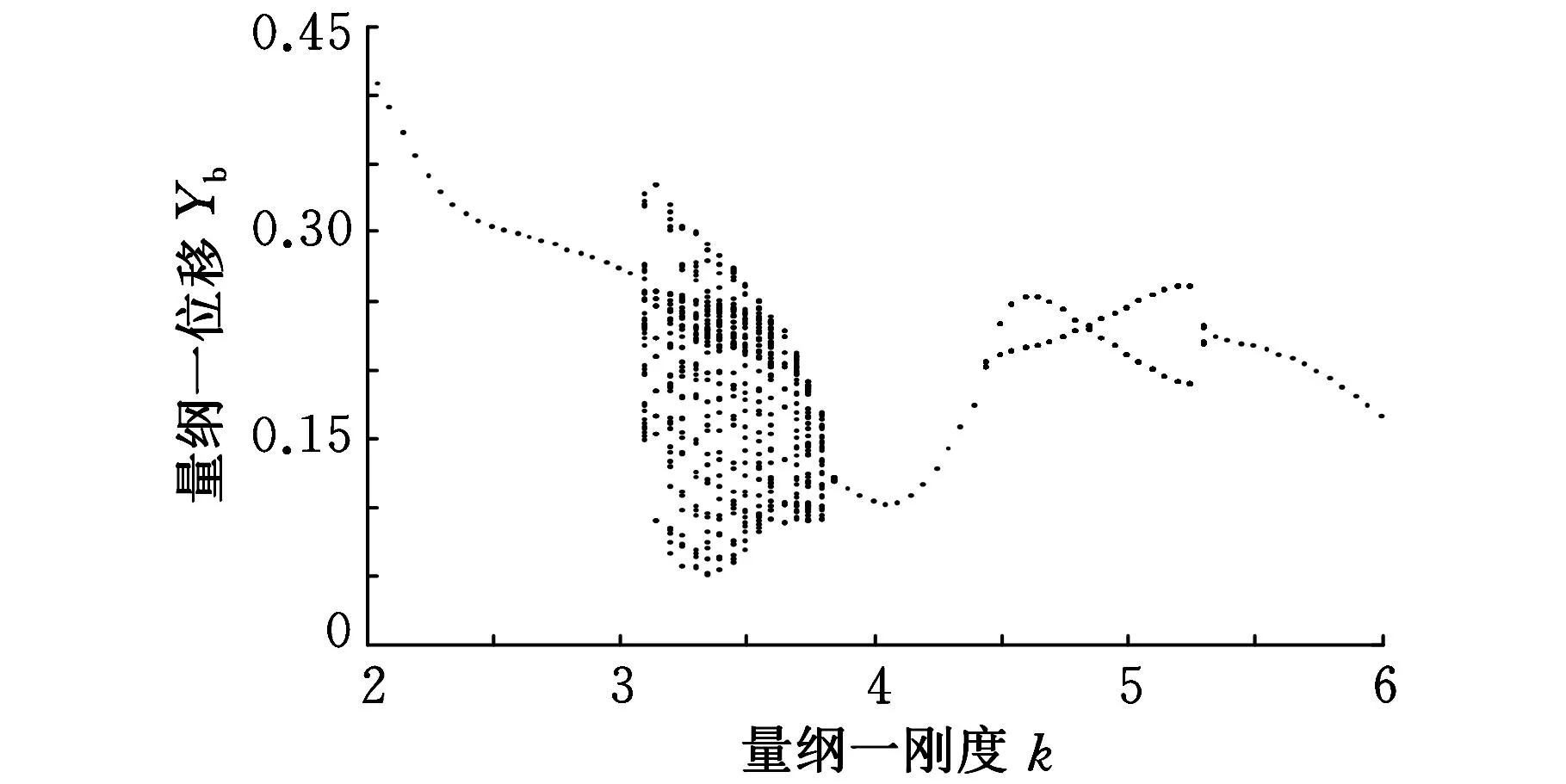
(b)圆盘处 图9　不同刚度下转子轴承处和圆盘处y方向的分岔图

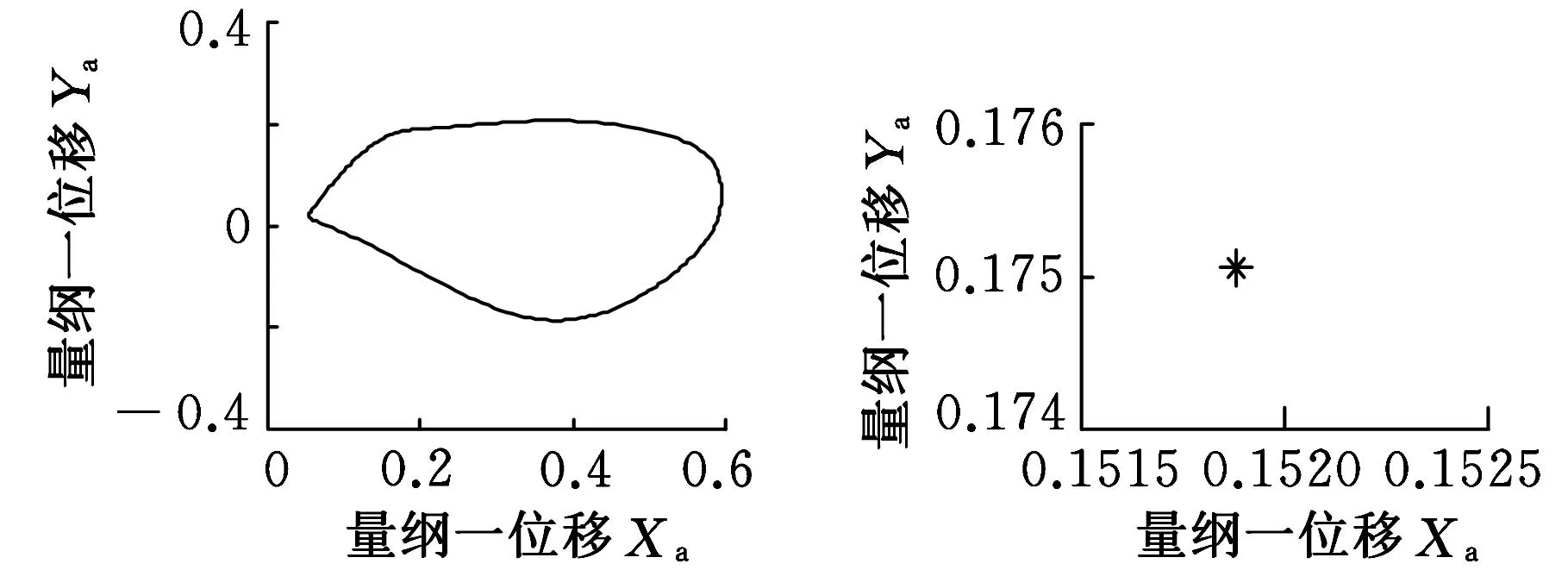
(a)周期轨迹(b)Poincaré映射点列 图10　转子轴承处的周期轨迹和 Poincaré映射点列(k=2.5)

(a)准周期轨迹

(b)Poincaré映射点列 图11　转子轴承处的准周期轨迹和 Poincaré映射点列(k=3.7)

(a)二周期轨迹

(b)Poincaré映射点列 图12　转子轴承处的二周期轨迹和 Poincaré映射点列(k=5.2)

3.3以圆盘处量纲一偏心量为控制参数

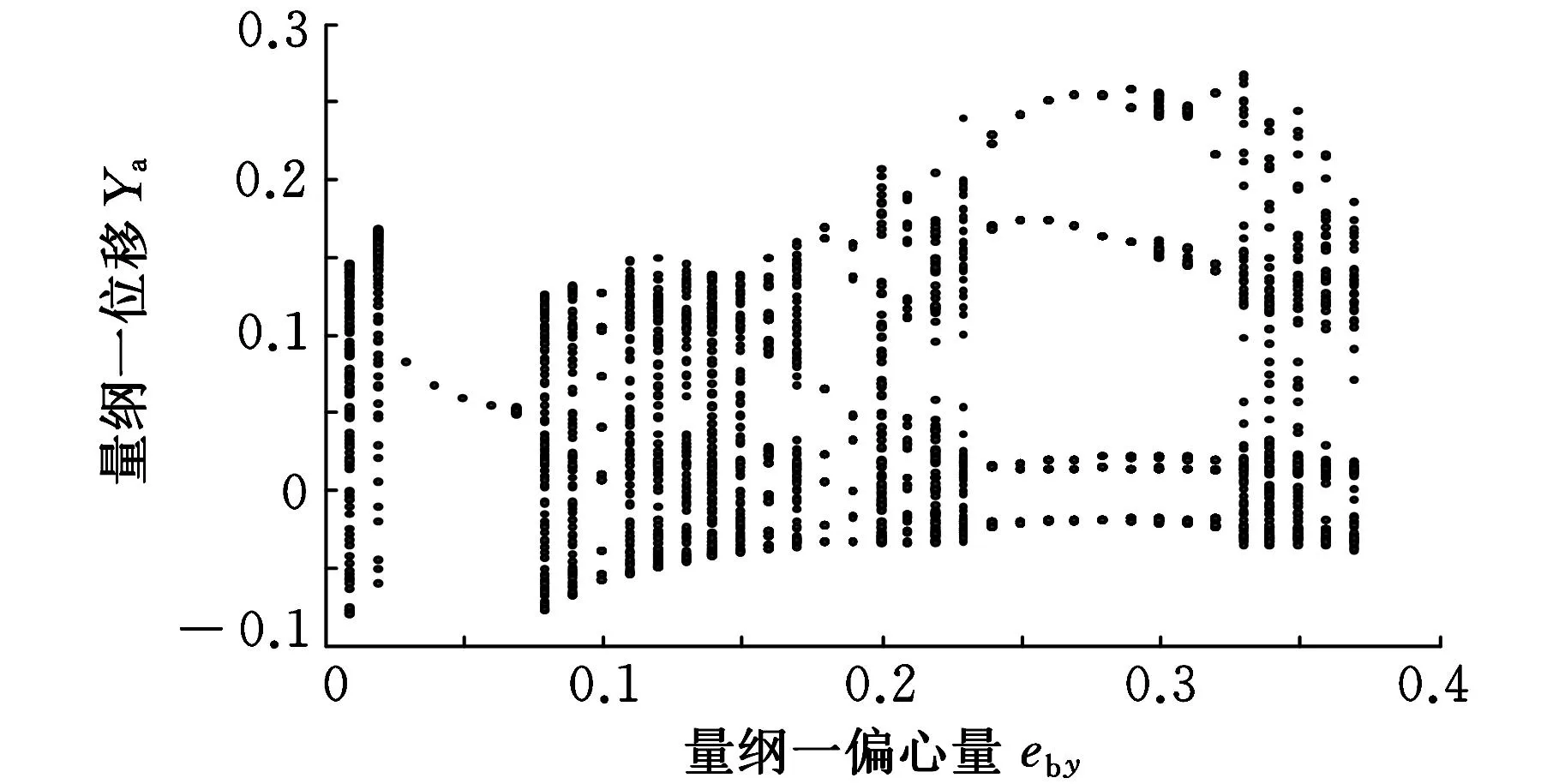
(a)轴承处

(b)圆盘处 图13　转子轴承处和圆盘处y方向的分岔图

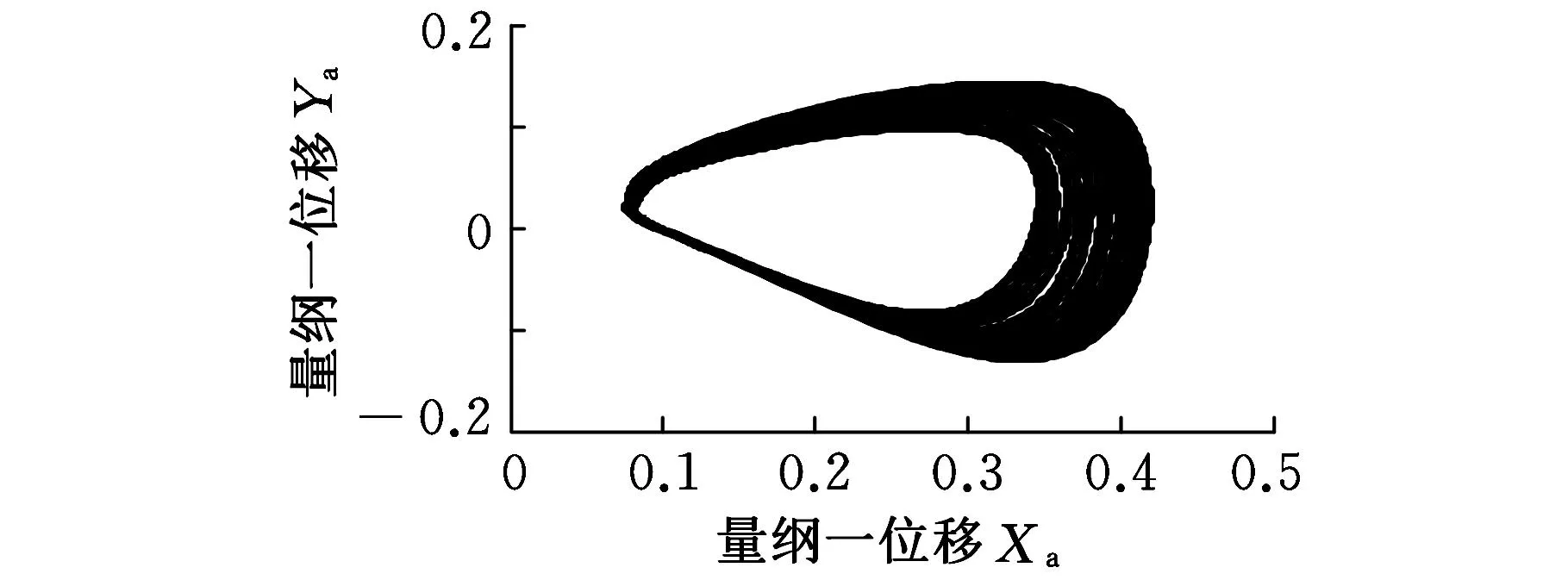
(a)准周期轨迹

(b)Poincaré映射点列 图14　转子轴承处的准周期轨迹和 Poincaré映射点列( =0.01)

(a)六周期轨迹

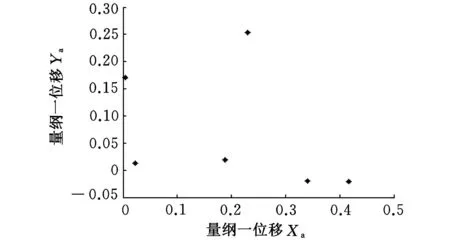
(b)Poincaré映射点列 图15　转子轴承处的六周期轨迹和 Poincaré映射点列( =0.27)

4结语

首先，本文基于有限长轴承模型假设，运用变分原理和分离变量法求得了有限长轴承的近似解析解。在求解雷诺方程的时候，将油膜压力分布函数P(φ，λ)看成是两个独立函数P*(φ)、ζ(λ)的乘积，其中，P*(φ)是关于φ的周向函数，ζ(λ)是关于λ的轴向函数。周向函数P*(φ)用无限长轴承假设下的油膜压力分布来代替，轴向函数ζ(λ)通过变分原理求得。在求得P*(φ)和ζ(λ)之后便可以求出有限长轴承油膜力的近似解。将本文提出方法的计算结果与有限元和无限长轴承模型的计算结果进行比较可知，本文提出的方法与有限元的计算结果非常接近，而且计算速度要比有限元方法的计算速度快很多，即本文提出的油膜力计算方法不仅能够保证计算的精确度，而且还能够提高计算效率，节约大量计算时间。

在求得有限长轴承油膜力近似解的基础上，分别以转轴的角速度、转轴的刚度和圆盘的偏心量为控制参数，运用轨迹图、Poincaré映射图、时间历程和分岔图分析了对称柔性转子-轴承系统的非线性动力学行为。从计算的结果可以看出，转子的非线性运动行为是非常丰富复杂的，呈现出周期、倍周期、准周期、六周期、十周期等非线性动力学现象。

参考文献：

[1]Wang Ligang，Cao Dengqin，Huang Wenhu. Nonlinear Coupled Dynamics of Flexible Blade-rotor-bearing Systems[J]. Tribology International，2010，43(4)：759-778.

[2]Castroa H F，Cavalca K L，Nordmann R. Whirl and Whip Instabilities in Rotor-bearing System Considering a Nnonlinear Force Model[J]. Journal of Sound and Vibration，2008，317(1/2)：273-293.

[3]Xie Wenhui, Tang Yougang, Chen Yushu. Analysis of Motion Stability of the Flexible Rotor-bearing System with Two Unbalanced Disks[J]. Journal of Sound and Vibration, 2008, 310(1/2): 381-393.

[4]Jing Jianping, Meng Guang, Sun Yi, et al. On the Non-linear Dynamic Behavior of a Rotor-bearing System[J]. Journal of Sound and Vibration, 2004, 274(3/5): 1031-1044.

[5]Wang Junguo, Zhou Jianzhong, Dong Dawei, et al. Nonlinear Dynamic Analysis of a Rub-impact Rotor Supported by Oil Film Bearings[J]. Archive of Applied Mechanics, 2013, 83(3): 413-430.

[6]Wang Jianke, Khonsari M M. Bifurcation Analysis of a Flexible Rotor Supported by Two Fluid-film Journal Bearings[J]. ASME Journal of Tribology, 2006, 128(3): 594-603.

[7]Li Dexin, Xu Jianxue. A Method to Determine the Periodic Solution of the Non-linear Dynamics System[J]. Journal of Sound and Vibration, 2004, 275(1/2): 1-16.

[8]Chang Jian，CaiWan. Non-linear Dynamic Analysis of Dual Flexible Rotors Supported by Long Journal Bearings[J]. Mechanism and Machine Theory, 2010, 45(6): 844-866.

[9]Wang Jianke, Khonsari M M. Effects of Oil Inlet Pressure and Inlet Position of Axially Grooved Infinitely Long Journal Bearings, Part I: Analytical Solutions and Static Performance[J]. Tribology International, 2008, 41(2): 119-131.

[10]Wang Jianke, Khonsari M M. Effects of Oil Inlet Pressure and Inlet Position of Axially Grooved Infinitely Long Journal Bearings, Part II: Nonlinear Instability Analysis[J]. Tribology International, 2008, 41(2): 132-140.

[11]Zheng Tiesheng, Yang Shuhua, Xiao Zhonghui, et al. A Ritz Model of Unsteady Oil-film Forces for Nonlinear Dynamic Rotor-bearing System[J]. ASME Journal of Applied Mechanics, 2004, 71(2): 219-224.

[12]Xiao Zhonghui, Wang Liping, Zheng Tiesheng. An Efficient Algorithm for Fluid Force and Its Jacobian Matrix in Journal Bearing[J]. ASME Journal of Triboogy, 2006, 128(2): 291-295.

[13]Vignolo G G, Barilá D O, Quinzani L M. Approximate Analytical Solution to Reynolds Equation for Finite Length Journal Bearings[J]. Tribology International, 2011, 44(10): 1089-1099.

[14]Hirani H, Athre K, Biswas S. Dynamically Loaded Finite Length Journal Bearings: Analytical Method of Solution[J]. ASME Journal of Tribology, 1999, 121(4): 844-852.

[15]Bastani Y, Queiroz M D. A New Analytic Approximation for the Hydrodynamic Forces in Finite-length Journal Bearings[J]. ASME Journal of Tribology, 2010, 132(1): 014502-1-9.

[16]Wang Yongliang, Liu Zhansheng, Kang Weijia, et al. Approximate Analytical Model for Fluid Film Force of Finite Length Plain Journal Bearing[J]. IMechE, Part C: Journal of Mechanical Engineering Science, 2012, 226(5): 1345-1355.

(编辑张洋)