基于KPCA-FSVM的液压泵可靠性寿命分布识别

基于KPCA-FSVM的液压泵可靠性寿命分布识别

景涛曹克强胡良谋高斌

空军工程大学，西安，710038

摘要：为了准确快速识别出液压泵的可靠性寿命分布模型，提出了一种基于核主元分析和模糊支持向量机的可靠性寿命分布模型识别方法。该方法充分利用核主元分析非线性特征提取的优势和模糊支持向量机良好的分类能力，建立了适合可靠性寿命分布识别的模糊支持向量机模型，并将其应用于液压泵可靠性寿命分布模型识别。仿真实验结果表明，该模型能够降低计算的复杂度，具有良好的泛化能力，能够准确地识别出液压泵无故障工作时间数据所属的寿命分布类型。

关键词：核主元分析；模糊支持向量机；寿命分布模型；液压泵；无故障工作时间

中图分类号：V24

收稿日期：2015-04-28

作者简介：景涛，男，1992年生。空军工程大学航空航天工程学院硕士研究生。主要研究方向为飞机液压系统可靠性。发表论文1篇。曹克强，男，1960年生。空军工程大学航空航天工程学院教授。胡良谋，男，1979年生。空军工程大学航空航天工程学院博士后研究人员。高斌，男，1992年生。空军工程大学航空航天工程学院硕士研究生。

Identification of Reliability Life Distribution of Hydraulic Pump Based on KPCA and FSVM

Jing TaoCao KeqiangHu LiangmouGao Bin

Air Force Engineering University，Xi’an，710038

Abstract:Aiming at identifying the reliability life distribution model of the hydraulic pump accurately and efficiently, an algorithm of KPCA and FSVM was brought forward. The recognition model of the reliability life distribution model was designed by making full use of advantages of the KPCA nonlinear feature extraction and the FSVM classification capacity, and might be used for identifying the reliability life distribution model of the hydraulic pump. The simulation results show that, the proposed method can reduce computation complexity, has good ability for generalization, and identify the life distribution type of life on time between failures of hydraulic pump accurately.

Key words：kernel principal component analysis(KPCA); fuzzy support vector machine(FSVM); life distribution model; hydraulic pump; time between failures

0引言

液压泵是飞机液压传动与控制系统中的能源部件[1]，是飞机液压系统的核心，随着液压系统日益高速化、复杂化及高精度化，人们对液压泵的安全性、可靠性要求越来越高[2]。

通过寿命分布模型来描述液压泵的可靠性是一种常用的数学方法，准确识别液压泵的寿命分布模型，是可靠性建模成败的关键，因此，研究液压泵可靠性寿命分布模型是极为重要的。

判断一组可靠性数据所属的寿命分布类型，主要有两类方法。传统的方法主要有解析法和图分析法，但在实际应用中，常常会出现几种分布同时满足要求，从而无法直接判断样本属于何种分布最佳。近年来，智能识别方法飞速发展，朱家元等[3-4]和韩强等[5]将其应用于可靠性寿命分布模型识别，实现了对常用的指数分布、威布尔分布、Г分布、对数正态分布、正态分布、Beta分布、均匀分布等的分类识别，识别率在90%以上。

为了简化计算的复杂度，进一步提高分类精度，本文提出了一种基于核主元分析(kernel principal component analysis，KPCA)[6-10]和模糊支持向量机(fuzzy support vector machine，FSVM)可靠性寿命分布模型识别方法。KPCA方法是Scholkopf等[11]对线性主元分析方法(principal component analysis，PCA)进行核化得到的一种新的多变量统计方法。由于核函数的应用，KPCA较PCA具有更多优势，尤其在非线性特征提取方面。FSVM能够克服SVM在解决多分类问题时存在的不可分区域问题，具有更好的分类性能。本文将KPCA与FSVM相结合，将经KPCA特征提取得到的主成分分量作为FSVM的输入建立寿命分布识别模型，并将该模型应用于液压泵可靠性寿命分布模型识别。

1基本原理

1.1核主元分析原理

核主元分析方法是在经典的主元分析的基础上，通过引入核函数，将数据映射到高维的特征空间，在高维空间使用PCA对其进行降维，以改善PCA在非线性数据情况下分析结果不理想的状况[6-10]。

对于原始数据样本集Xi(i=1，2，…，M)通过非线性映射Φ将Xi映射到新的特征空间F的像φ(xi)中。

定义映射数据的M阶对称方阵K的元素Kij为核函数：

Kij=φ(xi)φ(xj)i,j=1,2,…,M

(1)

式中，xi、xj为样本集Xi的两个样本；φ(*)为非线性映射函数。

若映射数据为非零均值，则需对核函数进行中心化处理：

(2)

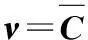
(3)

(4)

(5)

存在系数αj使得

(6)

成立。将式(4)、式(6)代入式(5)有

(7)

(8)

νk·νk=1

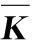
最后通过求累计方差贡献率来确定主元特征个数。累计方差贡献率定义为

(9)

1.2模糊支持向量机

SVM在解决多分类问题时，存在部分样本无法确切地属于某一类，从而产生不可分区域现象[12]。在“一对多”的情况下，假设第g类和其他类相区分开的第g个决策函数为

Dg(x)=wg·x+bg

(10)

式中，w为权向量；b为阀值；x为输入向量。

Dg(x)=0时，分类面为最优分类超平面。属于第g类的支持向量将满足Dg(x)=1，而属于其他类的支持向量将满足Dg(x)=-1。对于输入向量x，如果其中仅有一个类别满足D(x)>0，那么x将被划分到该类别中；但是当有多个类别同时满足式(10)或没有一个类别满足式(10)时，那么x是不可分的，从而形成不可分区域。

针对SVM在“一对多”模式中产生不可分区域问题，文献[13]提出了FSVM算法，在输入向量x满足不止一个类别，但却得到相同分类结果的情况下引入了一维成员函数。在垂直于分类超平面Dh(x)=0的方向上设置一维成员函数mgh(x)：

(1)当g=h时

(11)

(2)当g≠h时

(12)

g，h=1，2，…，n

利用mgh(x)，定义第g类隶属函数：

(13)

最终，一个待识别样本X所属的类别可由下式得到：

(14)

2基于KPCA-FSVM的寿命分布识别方法

本文提出的基于KPCA-FSVM的寿命分布模型识别方法步骤如下：

(1)确定初始样本集。选定所需的分布类型以及该分布函数的参数，根据分布类型及参数产生随机数，求出随机数组的数字特征并进行规则化处理，将处理后的数据作为初始样本集。

(2)核主元特征提取。通过KPCA对初始样本集进行核主元分析，当累积方差贡献率大于90%时，确定核主元特征个数，提取相应的主元特征向量作为FSVM模型的训练样本集。

(3)FSVM模型的训练及测试。设置FSVM的初始参数，将训练样本集输入到模型中进行训练，判断模型对训练样本集的识别率η，修改初始参数，直到模型对训练样本集识别率达到要求时停止训练。按照步骤(1)、步骤(2)产生测试样本集，将先测试样本集在主元方向上进行投影，提取主元向量并输入到模型中进行分类，得到模型对测试样本集的识别率。若识别率不满足要求，则重新调整FSVM的初始参数，直到满足规定要求，即得到FSVM寿命分布识别模型。

(4)实例应用。对未知分布类型的样本数据进行数字特征计算并进行规则化处理，将处理后的结果进行KPCA特征提取，构成待识别样本。将样本输入到模型中进行分类识别，即得到该组数据所属的分布类型。

基于KPCA-FSVM的可靠性寿命分布识别流程如图1所示。

3仿真实验及结果分析

3.1确定初始样本集

采用KPCA-FSVM模型对寿命分布进行识别，首先需要确定寿命分布模式。目前，在可靠性工程研究中所用的理论寿命分布类型很多，针对机械产品寿命这种连续型的随机变量，常用的分布形式主要有指数分布、正态分布、对数正态分布和两参数威布尔分布[14]。分析这4种分布在不同参数下概率密度函数的形状，然后对每种分布进行参数细分，共分为80种分布模式。细分后的分布模式如表1所示。

数字特征的选取对模型识别效果有着十分重要的影响。针对寿命分布模型的识别这类问题，通常是将提取样本集的峰度、偏度、离散系数、分位数等数字特征作为模型识别的特征，文中选择峰度、偏度、离散系数和7个分位数作为特征。

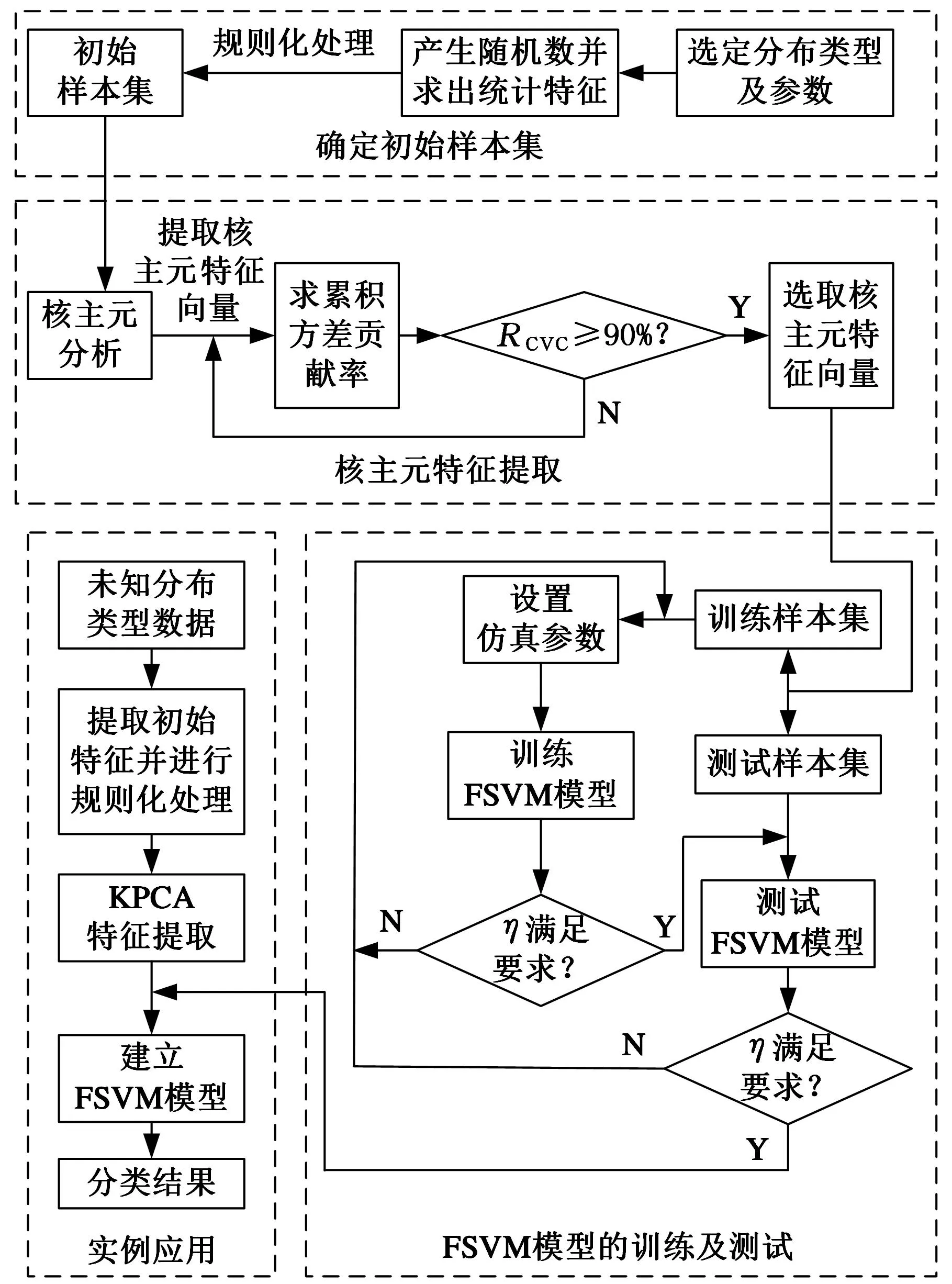
图1　基于KPCA-FSVM的寿命分布识别流程图

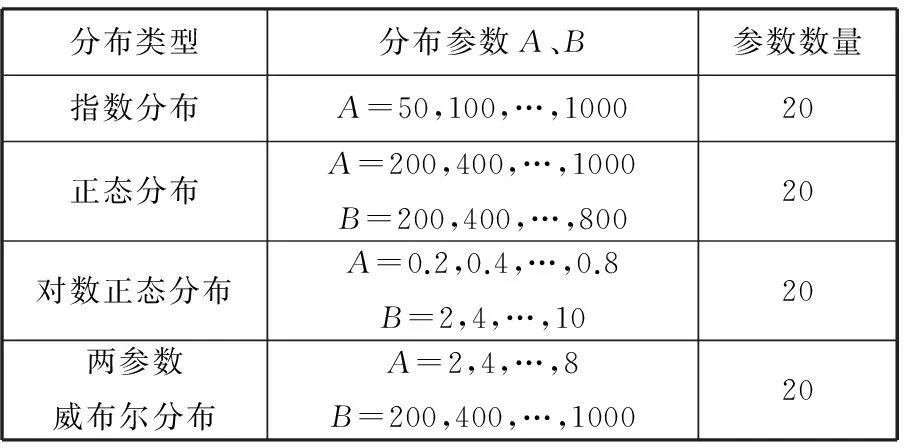
分布类型分布参数A、B参数数量指数分布A=50,100,…,100020正态分布A=200,400,…,1000B=200,400,…,80020对数正态分布A=0.2,0.4,…,0.8B=2,4,…,1020两参数威布尔分布A=2,4,…,8B=200,400,…,100020

用MATLAB产生以上80种不同分布模式的100个随机数组序列，求出该序列的数字特征并进行规则化处理，构建初始样本集，部分初始样本集如表2所示。

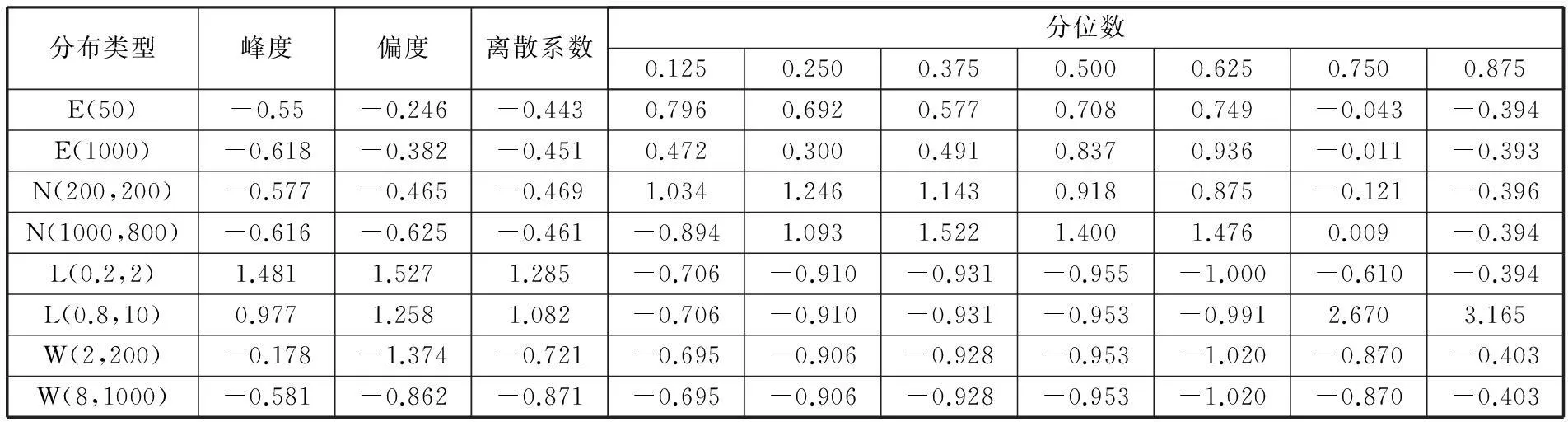
表2　部分初始样本集

注：E代表指数分布，N代表正态分布，L代表对数正态分布，W代表威布尔分布。

3.2核主元特征提取

对初始样本集进行核主元特征提取，首先对样本集进行核主元分析，核函数选择高斯径向基核函数：

(15)

经过多次取值试验，当σ取100时，前3个主元的累积方差贡献率大于95%，如图2所示。故核主元个数为3，将初始样本集在主元方向对应的特征向量作为FSVM模型的训练样本集。根据表1所列的4种分布，选择不包含表1中参数的4种分布(每种分布各10个)，通过产生随机数组序列，提取其数字特征，进行规则化处理，并在主元方向上进行投影，将投影后的结果作为FSVM模型的测试样本集。

图2　KPCA累计方差贡献率

3.3FSVM模型的训练及测试

本文通过编写FSVM的程序，构建FSVM寿命分布识别模型(规则化参数C=1000，总类别数为4)。核函数选取高斯径向基核函数

(16)

其中，x、x′为样本集的样本，参数σ=1。

将训练样本集和测试样本输入到FSVM模型中进行训练，调整模型参数，训练样本集和测试样本集满足识别率要求时停止训练，得到模型。本研究中规定，当模型对训练样本集和测试样本集的准确识别率均达到90%时，停止训练及测试。对于初始设定的参数，模型对训练样本集和测试样本集的识别率如图3、图4所示。

图3　KPCA-FSVM的训练样本集识别结果 (识别率为100%)

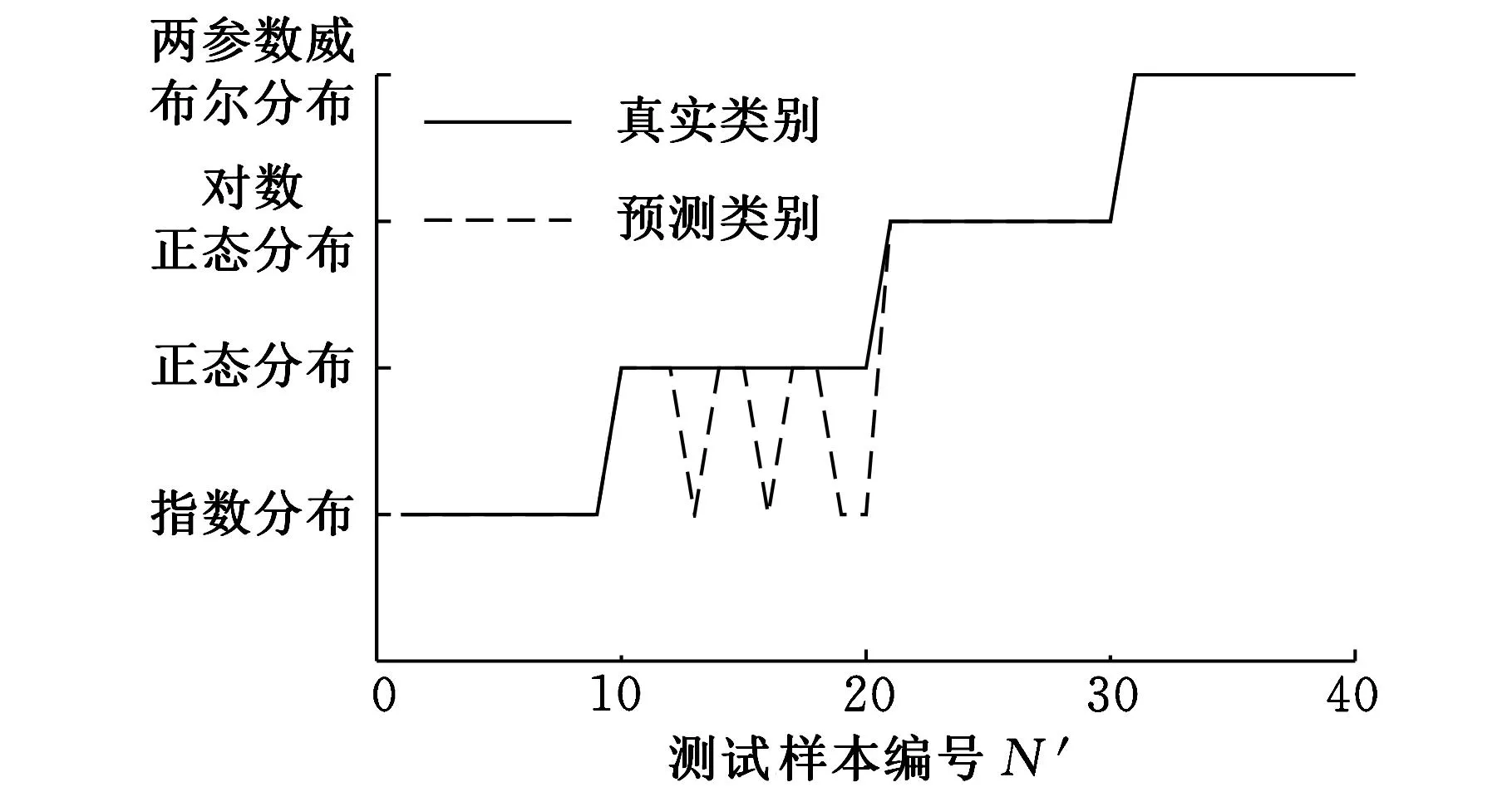
图4　KPCA-FSVM的测试样本集识别结果 (识别率为90%)

使用KPCA处理后的数据建立FSVM模型，模型对训练样本集和测试样本集的识别结果如图3、图4所示。模型对训练样本集识别率达到100%，对测试样本集的识别率达到90%，证明KPCA-FSVM模型具有良好的学习能力和推广性能，可以将该模型用于寿命分布模型识别。

为验证KPCA的性能，对未经KPCA处理的初始样本集进行训练，同时将产生的测试样本集输入到模型中进行分类识别，得到的结果如图5所示。

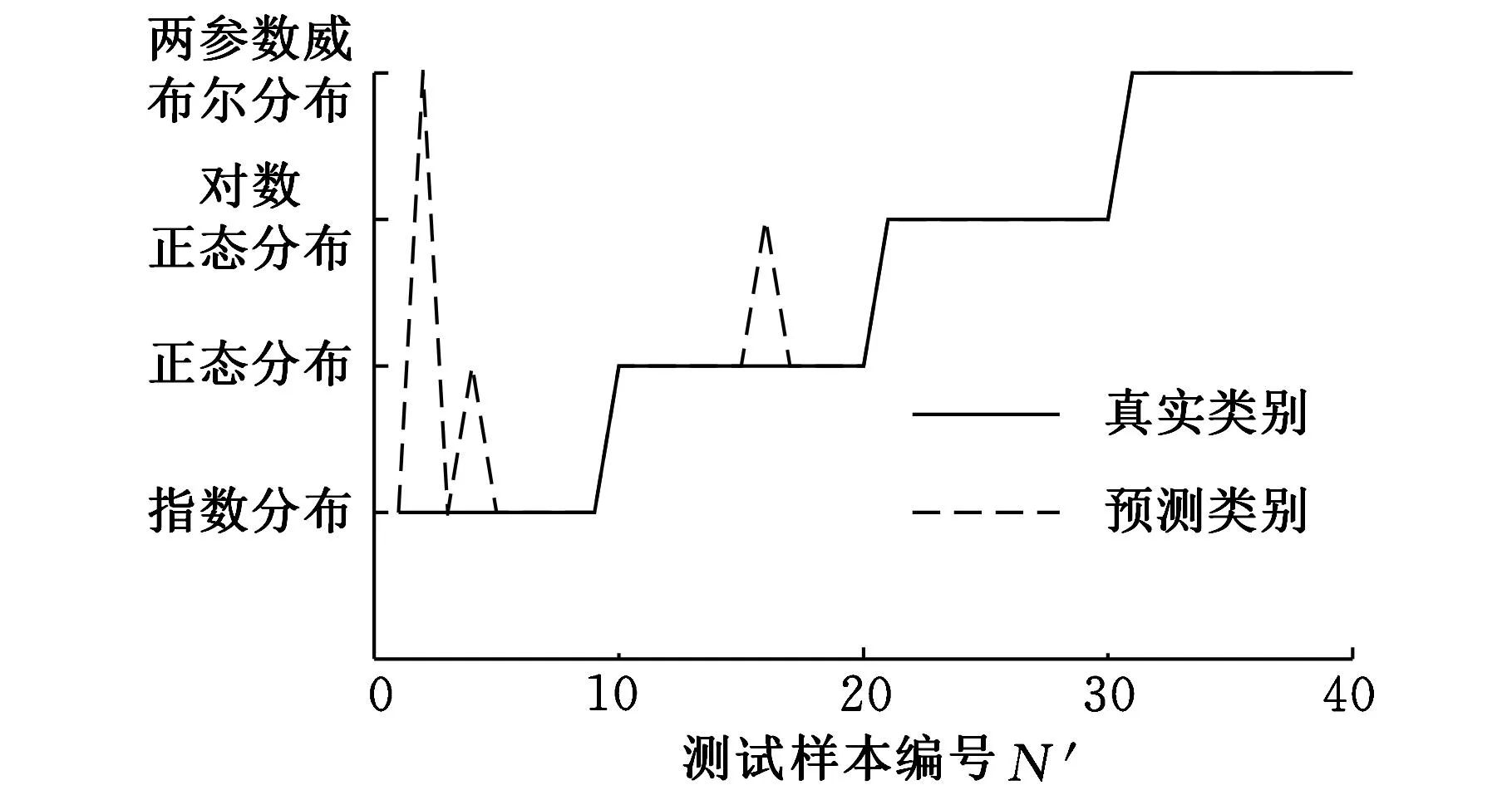
图5　FSVM的测试样本集识别结果 (识别率为92.5%)

图4、图5为KPCA-FSVM模型和FSVM模型对各自测试样本集的识别结果，准确识别率均在90%以上，表明KPCA-FSVM模型具有与FSVM模型相当的识别性能，使用KPCA对初始样本集进行核主元分析，提取核主元特征向量，保持了模型对样本的识别能力，同时经KPCA处理的初始样本集由高维降低为3维，大大简化了计算的复杂度。

仿真实验结果表明，KPCA可以对初始样本集数据进行非线性特征提取，有效降低了初始样本集的维数，使用提取的主元特征向量数据并结合FSVM可建立准确的寿命分布识别模型。KPCA-FSVM和FSVM两种方法建模的分类结果对比表明，KPCA-FSVM方法有效简化了计算，同时保证了识别的准确率，是一种更为有效的可靠性寿命分布识别方法。

4实例应用

对31台某型柱塞式液压泵进行寿命试验直至全部失效，首次失效时间依次为93h、100h、100h、100h、200h、200h、300h、300h、400h、400h、466h、500h、600h、600h、625h、700h、700h、800h、900h、900h、1000h、1000h、1100h、1206h、1402h、1622h、1700h、1900h、2000h、2200h、2400h。求出该组数据的数字特征并进行规则化处理。该液压泵的数字特征为-0.619、-0.394、-0.511、0.96、0.709、0.646、0.641、0.574、-0.136、-0.236。对该组数字特征进行核主元提取，将提取后的特征输入到模型中进行分类预测，分类结果如图6所示。

图6　液压泵寿命分布识别结果

实验预设样本的寿命分布类型为指数分布；通过模型进行预测分类得到的结果为指数分布。

对液压泵的无故障工作时间数据按置信度为95%进行极大似然估计，求出不同假设分布的参数，并使用k-s检验法判断该分布类型是否合理可用，其结果如表3所示。

表3　极大似然估计和k-s检验结果

对比传统方法和KPCA-FSVM判断该型液压泵寿命分布模型可知，使用传统假设检验方法时，通过k-s检验的分布有指数分布、正态分布、两参数威布尔分布，需要进一步进行判断才能得出准确的分布模型，而使用KPCA-FSVM方法对该型液压泵的无故障工作时间进行分类识别，可快速精确地得到该型液压泵的寿命分布模型属于指数分布。

5结语

基于KPCA-FSVM的寿命分布模型识别方法充分利用了KPCA提取非线性特征的优势，实现了对特征的降维处理。同时利用FSVM在处理多分类问题上的良好性能，建立了KPCA-FSVM寿命分布模型。该模型计算复杂度低、分类效果好，能够快速有效地实现对指数分布、正态分布、对数正态分布和两参数威布尔分布的分类识别。使用KPCA-FSVM方法对某型未知寿命分布模型的柱塞式液压泵寿命数据进行分类预测，得到的结果相比传统假设检验方法更为精确，证明了该方法的可靠性，具有一定的实用价值，便于工程应用。

参考文献：

[1]沈燕良.飞机系统原理[M]. 北京：国防工业出版社，2010.

[2]何庆飞，陈桂明，陈小虎，等. 基于灰色支持向量机的液压泵寿命预测方法[J]. 润滑与密封，2012，37(4)：75-77.

He Qingfei, Chen Guiming, Chen Xiaohu, et al. Life Prediction Method of Hydraulic Pump Based on Grey Support Vector Machines[J]. Lubrication Engineering, 2012，37(4)：75-77.

[3]朱家元，张恒喜，田松，等. 基于复合神经网络的数据分布模式仿真识别[J]. 系统工程与电子技术，2002，24(10):96-99.

Zhu Jiayuan, Zhang Hengxi, Tian Song, et al. Data Distribution Simulation Identification Using Combined Structure Neural Networks[J]. Systems Engineering and Electronics，2002，24(10):96-99.

[4]朱家元，张恒喜，张喜斌. 基于智能复合结构的可靠性分布模式自动识别[J]. 航空学报，2003，24(3)：207-211.

Zhu Jiayuan, Zhang Hengxi, Zhang Xibin. Reliability Distributions Automatic Identification Based on Intelligent Combined Structure Model[J]. Journal of Aviation， 2003，24(3)：207-211.

[5]韩强，祝华远，孙明礼，等. 基于支持向量机的小样本数据概率分布模式自动识别[J]. 科学技术与工程，2009，9(10)：2766-2769.

Han Qiang, Zhu Huayuan, Sun Mingli, et al. Modeling Distributions Identification for Small Samples Based on SVM[J]. Science Technology and Engineering, 2009，9(10)：2766-2769.

[6]郝惠敏, 汤晓君, 白鹏, 等. 基于核主成分分析和支持向量回归机的红外光谱多组分混合气体定量分析[J]. 光谱学与光谱分析，2008，28(6)：1286-1289.

Hao Huimin, Tang Xiaojun, Bai Peng, et al. Quantitative Analysis of Multi-component Gas Mixture Based on KPCA and SVR[J]. Spectroscopy and Spectral Analysis, 2008，28(6)：1286-1289.

[7]彭涛，杨慧斌，李建宝，等. 基于核主元分析的滚动轴承故障混合域特征提取方法[J]. 中南大学学报(自然科学版)，2011，42(11)：3385-3391.

Peng Tao，Yang Huibin，Li Jianbao，et al. Mixed—domain Feature Extraction Approach to Rolling Bearings Faults Based on Kernel Principle Component Analysis[J]. Journal of Central South University(Science and Technology), 2011，42(11)：3385-3391.

[8]宋平，文妍，谭继文. KPCA和遗传BP神经网络在滚珠丝杠故障诊断中的应用研究[J]. 机床与液压，2014，42(9)：159-162.

Song Ping，Wen Yan，Tan Jiwen. Application Research of KPCA and GA-BP Network in Ball Screw Fault Diagnosis[J]. Machine Tool & Hydraulic，2014，42(9)：159-162.

[9]周欣，吴瑛. 基于KPCA和LDA的信号调制识别[J]. 系统工程与电子技术，2011，33(7):1611-1616.

Zhou Xin, Wu Ying. Signal Modulation Recognition Based on KPCA and LDA[J]. Systems Engineering and Electronics, 2011，33(7):1611-1616.

[10]张曦，阎威武，刘振亚，等. 基于核主元分析和邻近支持向量机的汽轮机凝汽器过程监控和故障诊断[J]. 中国电机工程学报，2007，27(14)：56-61.

Zhang Xi，Yan Weiwu，Liu Zhenya，et al. Process Monitoring and Fault Diagnosis of Condenser Using KPCA and PSVM[J]. Proceeding of the CSEE, 2007，27(14)：56-61.

[11]Scholkopf B, Smola A, Muller K-R. Nonlinear Component Analysis as a Kernel Eigenvalue Problem[J]. Neural Computation, 1998，10(5)：1299-1319．

[12]陈家德，吴小俊. 自适应模糊支持向量机算法研究[J]. 计算机工程与应用，2010，46(25): 191-194.

Chen Jiade，Wu Xiaojun. Study on Adaptive Fuzzy Support Vector Machine Algorithm[J]. Computer Engineering and Applications, 2010，46(25): 191-194.

[13]Inoue T, Abe S. Fuzzy Support Vector Machines for Pattern Classification[C]//International Joint Conference on Neural Networks. Killarney，Ireland，2001：1449-1454.

[14]吴月明，王毅群，李莉. BP神经网络与广义RBF神经网络在产品寿命分布模型识别中的应用研究[J]. 中国机械工程，2006，17(20)：2140-2143.

Wu Yueming, Wang Yiqun, Li Li. Application Study on BP Network and Generalized RBF Network in Estimating Distribution Model of Mechanical Products[J]. China Mechanical Engineering, 2006，17(20)：2140-2143.

(编辑张洋)