复杂表面多轴数控加工精度控制

田 梅

(吉林工程技术师范学院机械工程学院，吉林长春130052)

数控加工技术的发展越来越迅速，特别是加工复杂表面技术，因其在航空航天、模具制造等领域的应用比较广泛，因此人们对其加工精度的要求也越来越高。在传统的加工方法中，不同的工序需在不同的设备上进行加工，多轴加工可以省去这个步骤，在节省加工时间的同时还能提高加工效率和加工精度。

1 复杂曲面多轴数控加工误差影响因素

1.1 多轴数控铣削加工误差产生原因

数控机床加工过程实际上是插补的过程，即把想要加工的曲线分割成很多小部分，然后用基本线型(一般为直线插补和圆弧插补)去拟合想要加工的曲线或曲面。加工前先根据零件图纸上的几何信息和工艺信息编写相应的程序。将加工程序输入数控机床中，再由数控装置控制机床主运动的变速、启动、停止、进给运动的方向、速度和位移量，以及刀具选择交换，工件装夹和冷却润滑的开关等动作［1］。加工曲面时由于要求的曲面精度不同，加工时会将其离散成一系列的微平面，因为加工过程中曲面上各点法矢量是变化的，所以刀轴矢量也是不断变化的，致使刀具接触点轨迹不同于先离散的曲线段，进而产生误差。

1.2 数控加工系统中的误差累积

在复杂表面加工过程中，对其精度产生影响的因素和误差来源有很多，比如工艺系统精度、机床运动精度、工艺系统的振动、热变形因素、数控编程技术、刀具类型、切削容差和切削间距、起刀点和进退刀方式、走刀方式等。而误差累积到一定程度就会严重影响待加工零件的表面质量，因此，应想办法减少累积的误差，直到满足精度要求。

2 加工误差自适应补偿方法及算法

2.1 补偿方法

加工误差补偿实际上是通过插补来实现的。数控装置根据输入的零件程序的信息，将程序段所描述的曲线的起点、终点之间的空间进行数据密化，从而形成要求的轮廓轨迹，对于复杂的形状，若直接生成算法会变得很复杂，计算机的工作量也会很大［2］。多轴数控加工过程中产生的插补误差属于非线性的。减小误差的方法有很多，比如线性加密法、刀位点自适应法等。为使加工过程中产生的误差在允许的公差范围之内，采用刀位点自适应补偿法使得刀位点的密化不过于复杂。

2.2 补偿算法

以转动轴为A、B轴的五轴数控铣床为例进行分析计算，并将其应用到后续的补偿算法中。

图1中，设(pw0，uw0)和(pw1，uw1)为相邻的刀位数据，对应于(pw0，uw0)的各联动控制轴的运动位置为(X0，Y0，Z0，A0，B0)，对应于(pw1，uw1)的运动位置分别为(X1，Y1，Z1，A1，B1)，则各轴运动为

图1 非线性误差示例

当机床做插补运动时，刀位点P的运动轨迹pw(t)为

［pw(t)，1］T=Qw，t［X(t)，Y(t)，Z(t)，A(t)，B(t)］·［pt，1］T.

记编程直线pwL(t)的方向矢量为

则pw(t)上任意点到pw(t)的距离ε(t)为

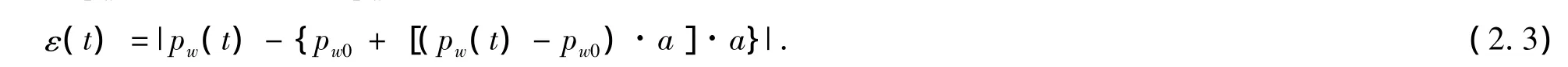
将ε(t)对时间t求导，即可得到最大误差εmax，若其比允许值大，则需在两刀位点中点处插入新的刀位点，然后再按照上述方法计算，校验误差是否在允许的范围内，若仍然不在范围内，则需再插入新的刀位点，直到达到精度要求。

3 复杂表面多轴数控加工精度建模

3.1 球头铣刀螺旋刃几何模型［3］

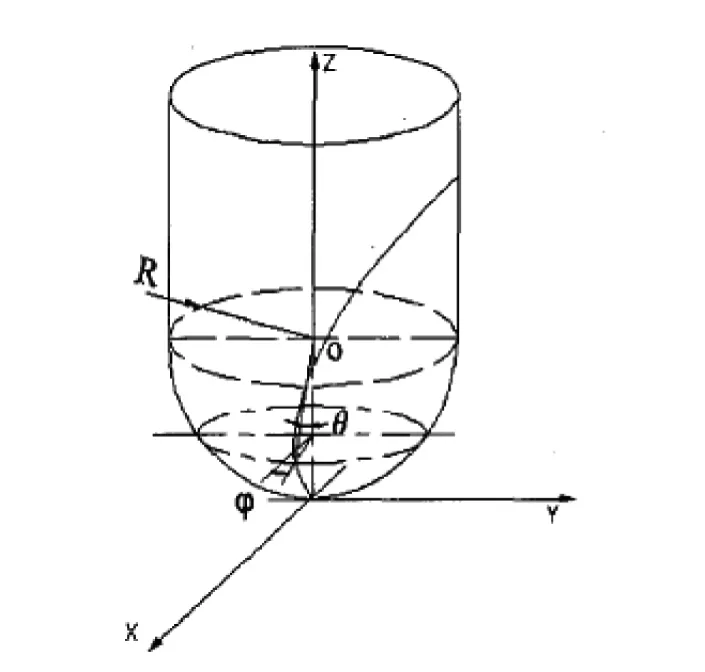
图2 球头铣刀

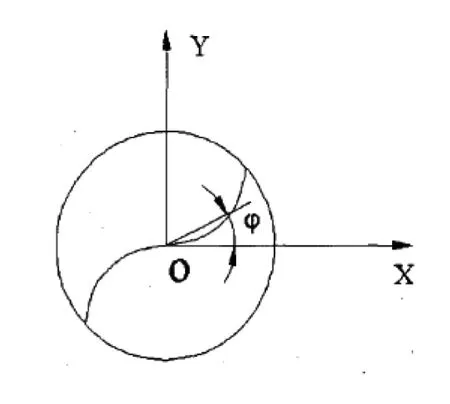
图3 二维刀头图

正交螺旋面方程的坐标为

球面方程的坐标系公式为

其中，R为铣刀球刃半径;θ为刀刃点和球心连线与刀具轴线夹角;φ为螺旋滞后角;P为螺旋面导程;Rc为刀刃点到刀具轴线间的距离。

由等距螺旋面与球面的交线得到铣刀的刃线方程，将方程(3.1)和(3.2)联立得到

φ =tanβ0(1－cosθ).

由此可见，当cosθ=0时，φ取得最大值φ0=tanβ0.

得到球头铣刀的刃线方程

4 应用实例

为了对比自适应补偿前后工件加工误差的大小是否发生变化，做两组实验。设计曲面的截面为正弦曲线，进行刀具路径规划、确定切削参数后，在第一组实验中使用CAXA制造工程师中自动生成的NC代码，在第二组实验使用进行误差补偿后改写的NC代码，得到的加工面如图4和图5所示。

图4 补偿前加工面图

图5 补偿后加工面

应用三坐标测量仪进行表面加工误差进行测量，测量前进行路径规划，得到采用误差补偿算法前后加工表面偏差如表1所示。从表1数据可以看出，采用补偿算法后的各项偏差值都在一定程度上得到了降低，达到了提高加工精度的目的。

表1 使用补偿算法前后零件的精度比较

5 结语

本文分析了复杂表面数控加工误差的影响因素，其中编程误差对加工精度的影响较大。结合实例得到采用误差补偿算法前后工件的加工的最大偏差值由+0.161/－1.041mm降到+0.145/－0.089mm，平均偏差值由 +0.054/－0.046mm 降到 +0.051/－0.028mm，标准偏差值由0.100mm 降到0.052mm，由此证明本文中提出的算法以及建立的模型是可行的、有效的。

［1］杨家坤.经济型数控机床的设计［J］.中小企业管理与科技:中旬刊，2014(6):248－249.

［2］于春海.机床数控系统插补算法的研究［J］.职业，2013(26):147.

［3］闫兵，徐安平，张大卫，等.一种新的螺旋刃球头铣刀铣削力模型［J］.中国机械工程，2002(2):160－163.