一类延迟微分方程Rosenbrock方法的数值Hopf分支

岳 双，张永坡，冯 雪

(空军航空大学基础部，吉林长春130022)

1 提出问题

延迟微分方程是泛函微分方程的一个重要分支，近年来很多学者研究了常微分方程的离散化格式对原连续的系统动力学性质的保持性，而对延迟微分方程相关内容的研究较少.英国V.Wulf等采用了Poincaré规范形进行计算［1］，目前很多学者将这种方法应用到各种模型中.张春蕊等证明了显式Euler方法对一类二维延迟微分系统Hopf分支结构的保持［2］;王秋宝等研究了Runge－Kutta方法对一类延迟微分系统Hopf分支性质的保持［3－4］.

考虑如下时滞为τ的延迟微分方程(其中时滞τ＞0，y∈Rd，是连续的初始函数):

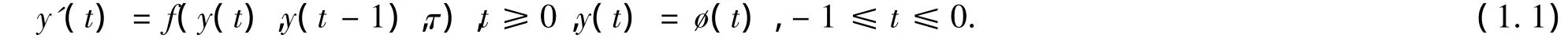
本文将讨论延迟微分系统(1.1).

将S级Rosenbrock方法:

应用于系统(1.1)，得到数值离散格式:

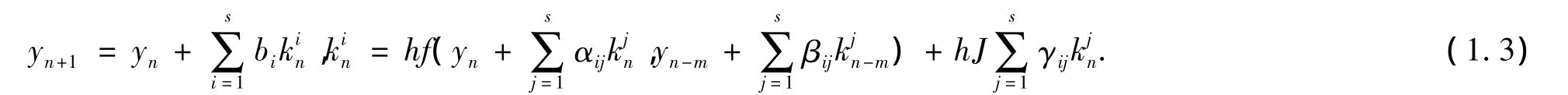
下列条件将保证在τ=τ*处系统(1.1)的零平衡点经历一个非退化的Hopf分支［1］.

(A1)f(0，0，τ)=0，当τ∈N(τ*)，N(τ*)是τ*的一个邻域(条件(A1)保证了对所有的τ∈N(τ*)，系统(1.1)的零点是平衡点);

(A2)当 τ∈ N(τ*)时，对于函数 f(x，y，τ)有

(A3)系统(1.1)在零点处的线性化的特征方程为(记μ=lnλ)

当 τ∈ N(τ*)时，该特征方程有一对简单的复共轭根 λ1，2= η(τ)e±iω(τ)，并且存在0 ＜ r ＜ 1，使得所有其他根的模小于r;

(A4)对于 τ= τ*，有 η(τ*)=1，ω(τ*)= ω0＞ 0;

(A5)η'τ(τ*)＞ 0;

(A6)非退化条件成立.

若假设(A3)～(A6)成立，则系统(1.1)经历一个Hopf分支;则零解在τ经过τ*时不是渐进稳定的(不失一般性，当从左到右时，由条件(A5)可知有一个小振幅的吸引周期轨出现(超临界Hopf分支)或一个排斥轨消失(下临界Hopf分支)).

2 数值Hopf分支的分支方向与分支不变曲线的稳定性

延迟微分方程Hopf分支分析的方法来自于Hassard等人众所周之的思想［5］.令τ=s+τ*，则可将系统(1.2)变换为 C=C(［－ 1，0］，Rd)上的延迟微分方程.

定义

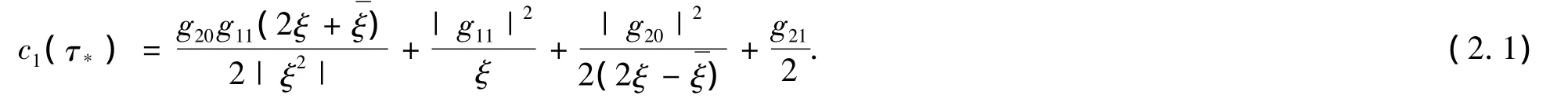
由文献［6］可知，Re c1(τ*)的符号确定了分支周期解的稳定性.

3 数值试验

为了验证得出的结论，考虑下列方程［7］:

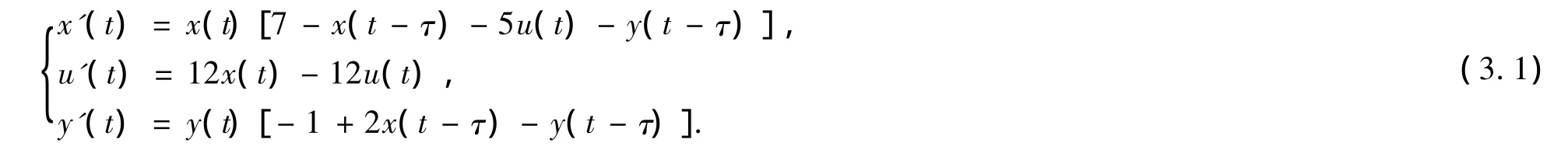
此系统有唯一的正平衡点E*(1，1，1)，可求出分支点τ*=1.0663，且有

(1)当τ＜τ*时，E*是稳定的(图1);(2)当τ经过τ*时，E*失去稳定性，经历Hopf分支，分支出周期解，且Hopf分支是超临界的，分支方向为τ＞τ*，且分支周期解是稳定的(图2).

图1 τ=0.9 ＜ τ*，平衡点E*(1，1，1)是渐近稳定的

图2 τ=1.2＞τ*，平衡点E*(1，1，1)处产生分支周期解，并且是渐进稳定的

将2级2阶Rosenbrock方法应用到方程(3.1)，其中，b1=0，b2=1，2，经计算可知其满足定理2.6的条件.得到相图如图3与图4所示，数值Hopf分支保持了分支方向与分支不变曲线的稳定性.

图3 应用2阶Rosenbrock方法，τ=0.9 ＜ τ*，h=0.01 时平衡点 E*(1，1，1)渐进稳定

图4 应用2阶Rosenbrock方法，τ=1.2 ＞ τ*，h=0.01时平衡点E*(1，1，1)处产生分支周期解，并且是渐进稳定的

［1］Ford NJ，Wulf V.Numerical Hopf bifurcation for the delay logistic equation［R］.Manchester Center for Computational Mathematics:Technical Report，1998，323.

［2］Zhang Chunrui，Liu Mingzhu，Zheng Baodong.Hopf bifurcation in numerical approximation of a class delay differential equations［J］.Appl Math Comput，2003，146:335 －349.

［3］Qiubao Wang，Dongsong Li.Numerical Hopf bifurcation of Runge – Kutta methods for a class of delay differential equations［J］.Chaos，Solitons and Fractals，2009，42:3087 －3099.

［4］M.Z.Liu，Qiubao Wang.Numerical Hopf bifurcation of linear multistep methods for a class of delay differential equations［J］.Applied Mathematics and Computation，2009，208:462 －474.

［5］Hassard BD，Kazarinoff ND，Wa YH.Theory and applications of Hopf bifurcation［M］.Cambridge:Cambridge University Press，1981.

［6］Wulf V，Ford NJ.Numerical Hopf bifurcation for a class of delay differential equations［J］.J Comput Appl Math，2000，115:601－616.

［7］马占平.几类非线性生物数学模型的动力学行为研究［D］.兰州:兰州理工大学，2008.