含股指期货的多资产价格动力学模型

王 婧

(伊犁师范学院数学与统计学院，新疆伊宁835000)

近几年，关于资产定价中有关异质代理商模型的研究受到很多学者的关注.大多数学者考虑两类资产，一支无风险资产，一支风险资产，主要探索影响期望收益和风险资产价格波动的因素，如 Gaunerdorfer［1］，Chiarella et al.［2］.大多数文献主要从两方面考虑问题:首先是制定均衡价格，做市商机制和Walrasian均衡机制，利用做市商机制更能体现真实市场的情况.如Chiarella et al.［3］利用做市商机制来出清市场价格.Mei Zhu和Chiarella［4］研究了在做市商机制中，当做市商扮演不同角色时，对市场的稳定的影响.其次是交易者更新信念的法则，其中二阶信念的应用更加广泛，并且对于在异质代理商模型中，处理多风险资产的问题也越来越多，如 Bhm and Chiarella et al.［5］，Wenzelburger［6］.

Chiarella et al［7］说明了趋势判断和时变信念的方差、协方差对价格与收益波动的影响.而且，风险或收益信念的改变可以引起一个风险资产到另一个风险资产的波动溢出.但其仅考虑了两种风险资产，没有考虑到两种资产的市场分数及其基本价格是由外生因素给定的.本文中，我们参考Chiarella et al［8］，考虑两类投资者，即基本面分析者与追风者，假定他们关于收益的一阶和二阶分布具有时变的信念，并考虑以一支风险资产为其标的股指期货与其本身之间外生相关性的联合影响.

1 模型

参考 Chiarella，Dieci，He［8］中的定理 1，有

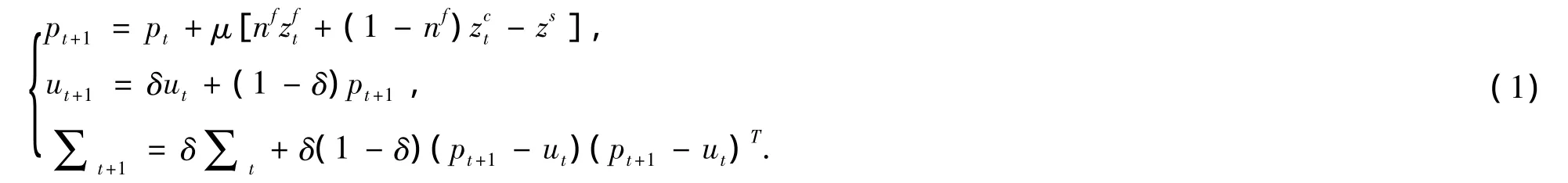
这里，我们也假设金融市场上有一种风险资产(i=1)和一种无风险资产，但同时加入以这种风险资产为标的的股指期货(i=2)，并且假定投资者对红利的期望值相同而股指期货的红利为零.对于基本面分析者来说，假设Eft(ct+1)=g(pt).股指期货定价模型参考Cornell和French［11］首次提出的当融资成本和股息收益用连续复利表示时的持有成本模型，那么指数期货定价公式为

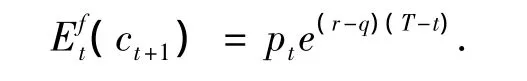
其中，ct为期货合约在t时的价值，pt为期货合约标的资产(股票指数)在t时的价值，r为无风险收益率，q为股息收益率，T为期货合约到期时间，t为现在的时间.

对于技术分析者来说，我们假设Ect(ct+1)=ct+d(ct－τ2，t).

参考 He［12］和 Chiarella et al.［7］，假设样本均值、方差过程遵循几何衰减过程:

τi，t+1= ωτi，t+(1－w)pi，t+1，vi，t+1= ωvi，t+ ω(1－ω)(pi，t+1－τi，t)2，(i=1，2).

本文假定外部供给为零，即zs=0.由此得到含股指期货的多资产价格动态模型

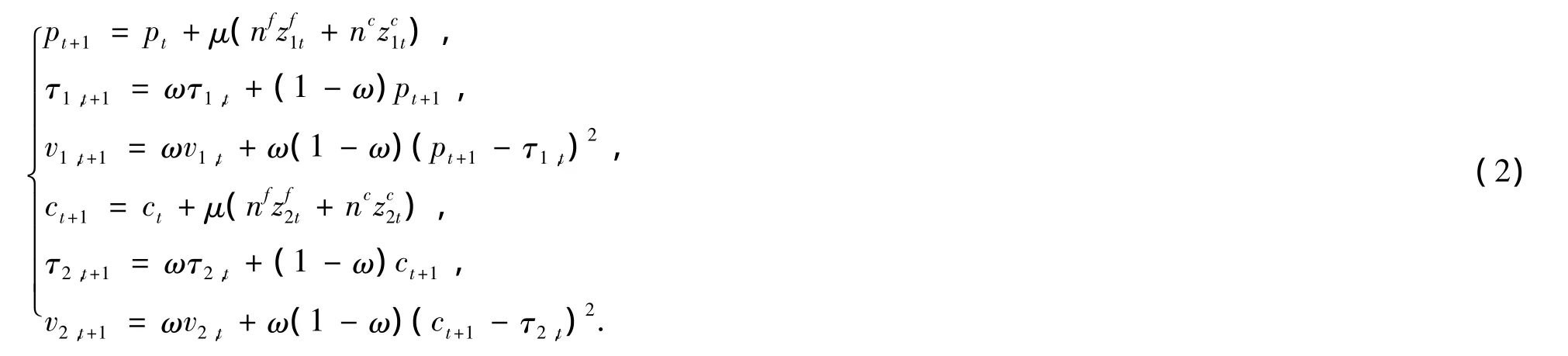
其中，

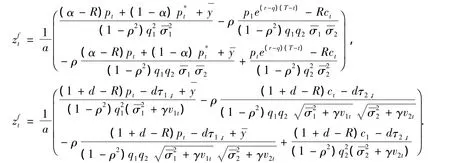
2 非线性系统的稳定性分析

6 维确定性动力系统由映射 J:(p，τ1，v1，c，τ2，v2)→ (p'，τ1'，v1'，c'，τ2'，v2')给出.

下面，我们讨论上述系统(3)的平衡点的存在性、稳定性、稳定性区域及分支情况.

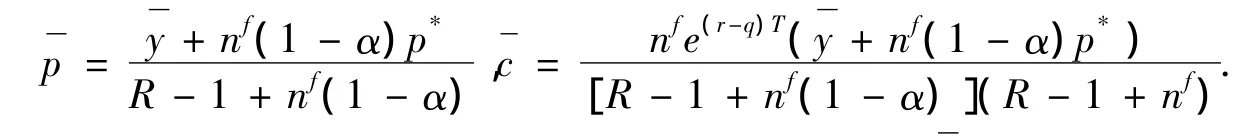
将p*代入上式，得到

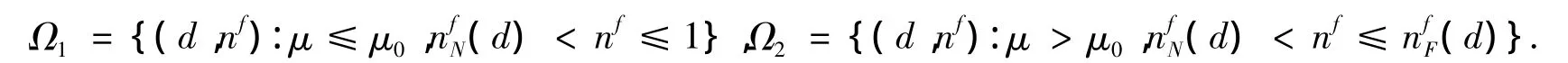
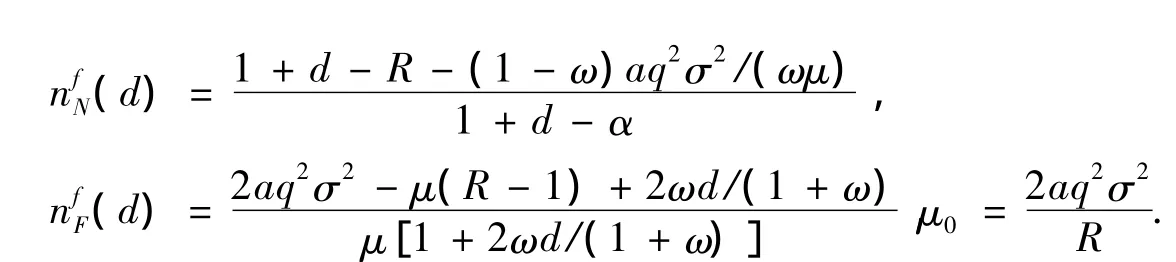
Γ(λ)=(λ － ω)2［λ2－(A+ω +B － ωB)λ +ωA］［λ2－(D+ω +E － ωE)λ +ωD］=(λ－ω)2Γ1(λ)× Γ2(λ).

λ1= λ2= ω是其特征根，其它特征根λi(i=3，…，6)满足Γ1(λ)× Γ2(λ)=0，由Jury’s判据知，特征根在单位圆内，即|λi|＜1，基本平衡点是稳定的，因0＜ω ＜1，所以只需计算λi(i=3，…，6)在单位圆内的参数范围.则需满足以下条件:①Γ1(1)＞0;②Γ1(－1)＞0;③|ωA|＜1.

①Γ1(1)=(1－ω恒成立，因R ＞1，0≤α≤1.

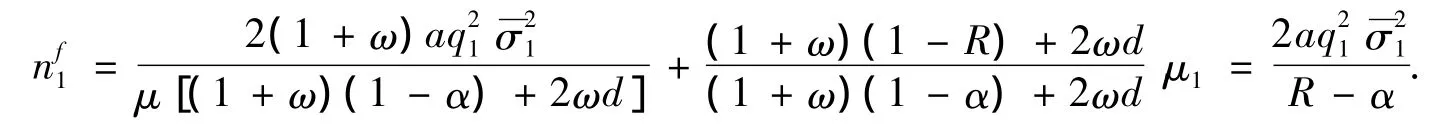
那么，Γ1(λ)的特征根在单位圆内的取值范围为nf2＜nf≤1，μ ＜ μ1，或nf2＜nf≤nf1，μ≥μ1，

同样，Γ2(λ)的特征根在单位圆内的取值范围为nf5＜ nf≤1，μ ＜ μ3，或nf5＜ nf≤nf4，μ ≥μ3，其中，nf4=

n f )］ .N(d)=1+d－R －(1－ ω)a q2σ2/(ω μ)F(d)=2 a q2σ2－ μ(R－1)+2 ω d μ/(1+ ω)μ［1+2 ω d/(1+ ω+d－a ，nf1

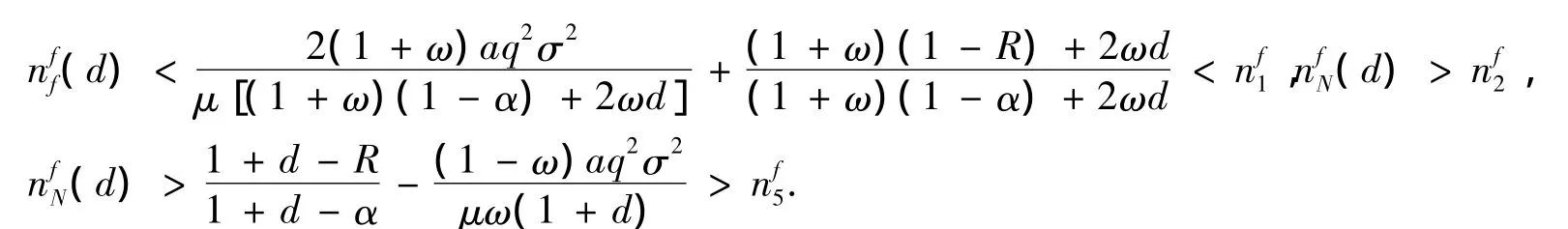
综上，Γi(λ)(i=1，2)的特征根在单位圆内同时成立，得到

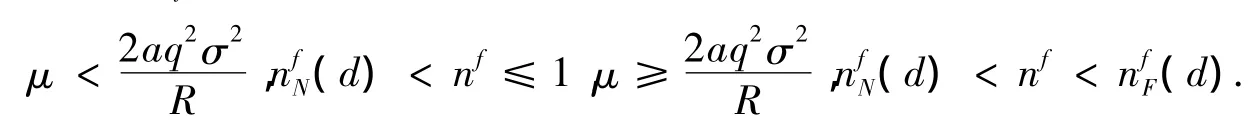
另外，当nf=nfF(d)时，Γ(λ)=0中一个特征根为－1;当nf=nfN(d)时，有一对共轭复根.因此，当μ=μ0时，在 nf=nfF(d)边界上产生Flip分支;在nf=nfN(d)边界上产生Hopf分支.

图1 (d，nf)平面上稳定区域Ⅰ

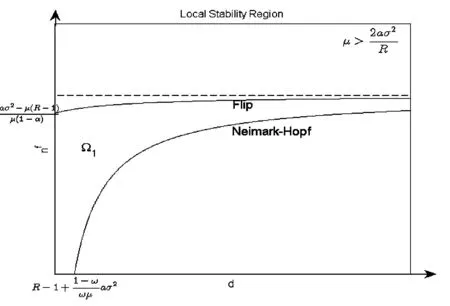
图2 (d，nf)平面上稳定区域Ⅱ

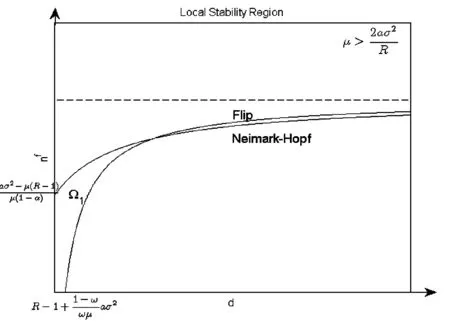
图3 (d，nf)平面上稳定区域Ⅲ

图1、图2和图3画出了(d，nf)平面上的三个稳定区域，参数选择如下:R=1.0002;r=0.05;σ21=0.9;q2=1;σ22=1.6;ω =0.5;α =0.75;a=0.05.其中，μ 分别为0.07，0.1，0.18.随着 μ 的增大，Flip 分支边界与Hopf分支边界会相交，稳定区域也会逐渐减小.因为我们考虑的是追风者，即d＞0的情形.令nfF(d)=nf(d)，解得 d=N，只要满足d＞0，即只要Flip分支边界与Hopf分支边界就会相交。

3 结语

本文在做市商机制下，多资产模型的基础上，建立了一支风险资产以及与其标的的股指期货两类资产定价模型.运用差分系统稳定性理论，讨论特殊情形下系统的稳定区域与分支情况.由此得到做市商的调整速度、基本面分析者的调整速度等主要参数对系统稳定区域的影响以及分支的变化情况.

［1］Gaunersdorfer，A.Endogenous fluctuations in a simple asset pricing model with heterogeneous agents［J］.Joutnal of Economic Dynamics and Control，2000(24):799 －831.

［2］Chiarella C，Dieci R，Gardini L.Speculative behaviour and complex asset price dynamics:a global analysis［J］.Journal of E-conomic Behavior＆ Organization，2002，49(2):173 －197.

［3］Chiarella C，He X Z.Heterogeneous beliefs，risk and learning in a simple asset pricing model with a market maker［J］.Macroeconomic Dynamics，2003(7):503 －536.

［4］Zhu，M.，Chiarella，C.，He，X.，et al.Does the market maker stabilize the market［J］.Physica ，2009，388:3164 －3180.

［5］Bhm.，Chiarella，C.Mean variance preferences，expectations formation and the dynamics of random asset prices［J］.Mathematical Finance，2005，15(1):61 －97.

［6］Wenzelburger，J.Learning to predict rationally when beliefs are heterogeneous［J］.Joutnal of Economic Dynamics and Control，2004，28(10):2075 －2104.

［7］Chiarella C，Dieci R，Gardini L.The dynamic interaction of speculation and diversification［J］.Applied Mathematical Finance，2005，12(1):17 －52.

［8］Chiarella C，Dieci R，He X Z.Heterogeneous expectations and speculative behavior in a dyn－amic multi－ asset framework［J］.Journal of EconomicBehavior＆ Organization，2007，62:408 －427.

［9］Brock，W.，＆ Hommes C.H.Heterogeneous beliefs and routes to chaos in a simple asset pricing model［J］.Journal of Economic Dynamic ＆ Control，1998(22):1235 －1274.

［10］Chiarella C，He X Z.Heterogeneous beliefs，risk and learning in a simple asset pricing model［J］.Computational Economics，2001(19):95－132.

［11］Cornell B，French K.R.The pricing of stock index futures［J］.Journal of Futures Markets，1983，3(1):1 －14.

［12］He X.Asset pricing，volatility and market behaviour:a market fraction approach［M］.Sydney:School of finance and Economics，University of Technology，2003.

［13］王联，王暮秋.常差分方程［M］.乌鲁木齐:新疆大学出版社，1991:202－204.