一类广告扩散模型的Hopf分岔分析
丁学利
(阜阳职业技术学院 基础教学部,安徽 阜阳 236031)
1 引言
对分岔问题的研究可以追溯到十八世纪,人们对天体力学、流体力学、弹性力学和非线性振动中的一些失稳现象的探讨,因此分岔问题有着深刻的应用背景.目前在物理学、化学、生物学、工程技术以及经济学和社会学中都有着广泛的应用[1,2].
Hopf分岔是一类很重要的分岔问题,它不仅有着重要的理论价值,而且在实际问题中有着广泛的应用.本文利用分岔理论详细讨论了一类广告扩散模型平衡点的稳定性和Hopf分岔,并且给出了发生Hopf分岔的参数条件,最后数值仿真验证了理论推导的正确性.这对研究广告扩散模型的实际应用,提供了理论依据.
2 广告扩散模型平衡点的稳定性
考虑如下的广告扩散模型[3,4]:

其中β,ε,k均为正常数,设置 α 为分岔参数.系统(1)有唯一的平衡点,在平衡点E0处的Jacobian矩阵为
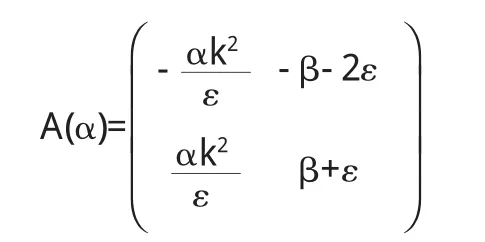
其特征方程为
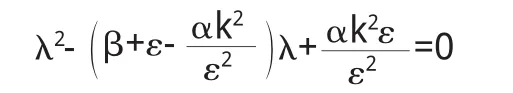
即 λ2-trA(α)λ+detA(α)=0,因此令 μ(α0)=0,得
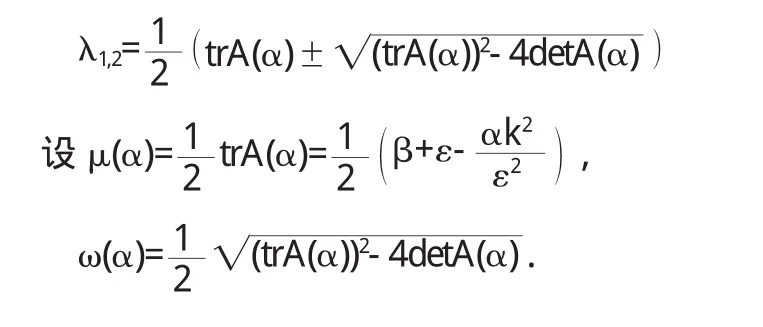
且 ω2(α0)=detA(α0)=(β+ε)ε>0.
定理 1 (1)当 α>α0时,若(trA(α))2-4detA(α)>0(<0),则特征方程的根为两个相异的负实根(一对具有负实部的共轭复根),从而系统(1)的平衡点是稳定的结点;
(2)当 0<α<α0时,若(trA(α))2-4retA(α)>0(<0),则特征方程的根为两个相异的正实根(一对具有正实部的共轭复根),从而系统(1)的平衡点是不稳定的焦点,即有可能发生Hopf分岔.
3 广告扩散模型的Hop f分岔
定理 2 当0<α<α0时,系统(1)发生Hopf分岔.
证明 根据文献[3],只需要验证两个条件,即μ'(α0)≠0(横截条件)和 l1(α0)≠0(非退化条件为第一李雅普诺夫系数).
首先横截条件很容易证明:
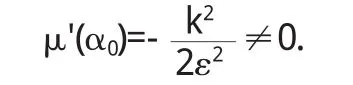
下面计算第一李雅普诺夫系数.
在α=α0处,平衡点E0的坐标为
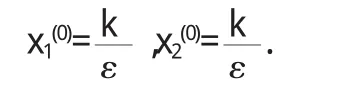
作坐标变换
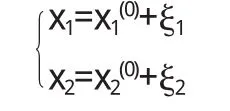
这样就把平衡点E0变到坐标原点,系统(1)化成:
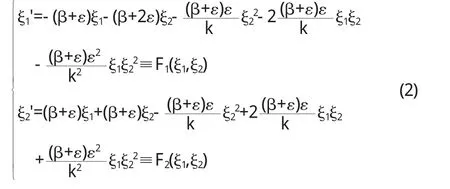
系统(2)可表示为下面的形式:
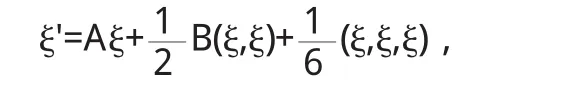
其中A=A(α0),多线性函数B和C'是关于平面向量ξ=(ξ1,ξ2)T,η=(η1,η2)T,ζ=(ζ1,ζ2)T的函数,其值为

满足 Aq=iωq,ATq=-iωq,且〈p,q〉=1.
第一李雅普诺夫系数为

其中

所以满足非退化条件 l1(α0)≠0.因此,在 0<α<α0处发生Hopf分岔,产生稳定的极限环.由于l1(α0)<0,所以是超临界Hopf分岔.
4 数值仿真
下面我们将用Matcont软件来分析广告扩散模型的动力学行为,其参数使用为β=0.5,ε=k=9.5,α为分岔参数.
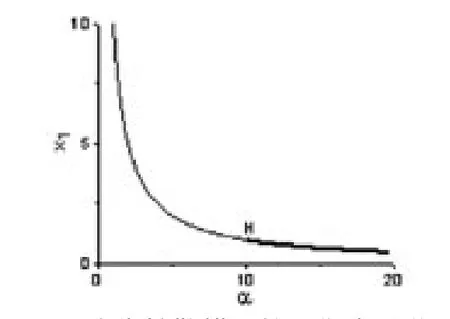
图1 广告扩散模型的平衡点分岔图
图1是广告扩散模型的平衡点分岔图,粗实线表示稳定的结点,细实线表示不稳定的焦点,H表示Hopf分岔点,此时α0=10是发生Hopf分岔的临界点.
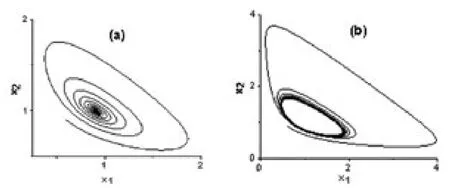
图2 广告扩散模型的相图.(a)α=11>α0;(b)α=9.5<α0
图2是广告扩散模型的相图.当α=11>α0时,系统的平衡点是渐进稳定的(图 2(a));当 α=9.5<α0时,系统产生稳定的极限环(图 2(b)),即发生了 Hopf分岔.
5 讨论与结论
本文对广告扩散模型平衡点的稳定性进行了研究,并且证明了系统发生Hopf分岔的参数条件.结果表明在一定条件下,系统发生Hopf分岔是超临界的.最后,数值仿真验证了理论推导的正确性.此外,系统还有一些性质需要进一步的分析,如极限环如何消失,是否发生同宿轨分岔,以及能否出现混沌等.
〔1〕刘秉正,彭建华.非线性动力学[M].北京:高等教育出版社,2004.
〔2〕张琪昌,王洪礼,等.分岔与混沌理论及应用[M].天津:天津大学出版社,2005.
〔3〕KUZNETSOV.Yuri A.Elements of applied bifurcation theory[M].New York:Springer,1997.
〔4〕FEICHTINGER.G.Chaotic behavior in an advertising diffusion model[J].Internation Journal of Bifurcation and Chaos:1995.

