非高斯噪声驱动下捕食——食饵模型的平均首次穿越时间研究
张晓燕
(西安建筑科技大学 数学系,陕西 西安 710055)
1 引言
近年来,考虑噪声对非线性生物系统的影响引起一些研究者的关注.在生物系统的研究中随机共振、噪声诱导相变等噪声的影响效应也陆续被发现[1-5].
捕食-食饵模型被用于分析带免疫细胞的癌细胞增长模型.Fiasconaro等人[3]考虑了带免疫响应的癌细胞增长系统并分析了噪声强度对平均首次穿越时间与首次穿越时间的不同影响.之前的研究中,多数情况下主要考虑高斯噪声对生物系统的影响.但是许多实验表明在生物系统中其噪声源应该是非高斯噪声[6-7].因此,本文主要研究基于非高斯噪声激励的捕食-食饵模型在加性噪声与乘性噪声之间为白关联情形下的平均首次穿越问题.
2 捕食-食饵模型中的平均首次穿越时间
考虑有如下方程所描述的由非高斯噪声影响下的捕食-食饵模型:
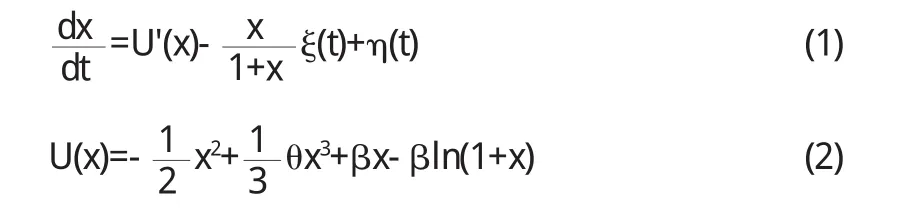
U(x)为系统确定性势函数,当 θ<1,0<β<(1+θ)2/4θ 时,该系统是双稳的,且有一个不稳定态x0和两个稳定定态x+,x-,分别为:
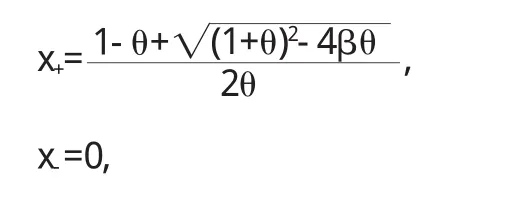

若取 θ=0.1,β=2.8,则 x+=6,x-=0,x0=3.
在(1)式中,η(t)为高斯白噪声,ξ(t)为非高斯噪声并满足如下方程:
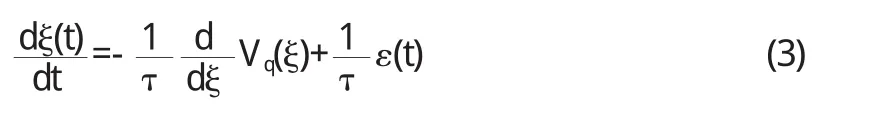
并且

这里ε(t)为高斯白噪声,η(t)和ε(t)之间满足的统计性质为:

其中D和α分别表示乘性和加性白噪声强度.λ为ε(t)和η(t)之间的关联强度.参数q表示ξ(t)偏离高斯分布的程度,由文献[7]可以得到ξ(t)的一二阶矩为:

应用路径积分法,可以得到,
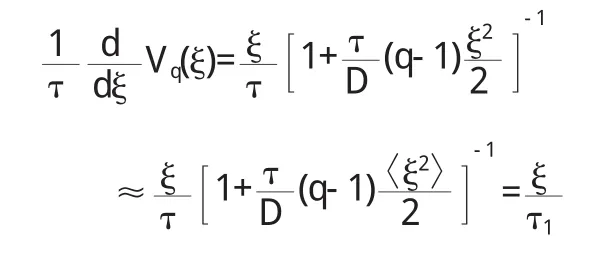
其中

若q→1,则非高斯噪声ξ(t)就退化高斯色噪声.它的有效关联时间为τ1,相应的有效关联强度为

由(7)和(8)式可知,当 q→1时,有 τ1→τ和 D1→D.
因此,方程(3)可写为:

并且

根据上述分析,可以得到系统相应的近似的福克-普朗克方程(FPE)如下:

其中,

根据(11)式,可以得到系统的稳态概率密度函数为:

其中,N是方程(12)的归一化常数,U軒(x)为广义势函数,其表达式如下:

根据平均首次穿越时间的定义以及最速下降法[8],我们可以得到两个不同方向的平均首次穿越时间T+(x+→x-)与T-(x-→x+),下文中将“T+(x+→x-)”与“T-(x-→x+)”分别简化为“T+”和“T-”,它们的表达式如下所示:
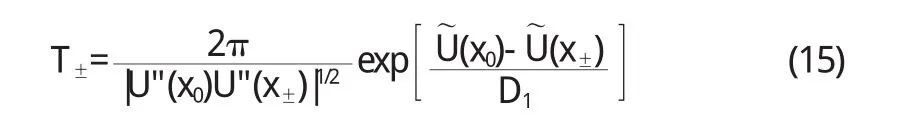
3 噪声对平均首次穿越时间的影响
根据(15)式,可以讨论关联非高斯与高斯噪声对两个方向平均首次穿越时间的影响.
图1和图2描述了平均首次穿越时间T+和T-作为乘性噪声强度D的函数随着不同的噪声互关联强度λ变化的曲线.从两图可以看出,乘性噪声强度与噪声互关联强度对两个方向的平均首次穿越时间T+和T-的影响是类似的.当噪声互关联强度取值为负时(λ=-0.7,-0.3),T+与T-随着乘性噪声强度的增加单调减小;而当噪声互关联强度取值为正时(λ=0.3,0.7),T+与T-随着乘性噪声强度的增加先增加再减小,有极大值出现,两曲线都存在共振峰,并且随着λ的增加共振现象越发明显.共振现象表明系统稳定性增强不易发生相变.

图1 T+作为乘性噪声强度D的函数随着噪声关联强度λ变化的曲线
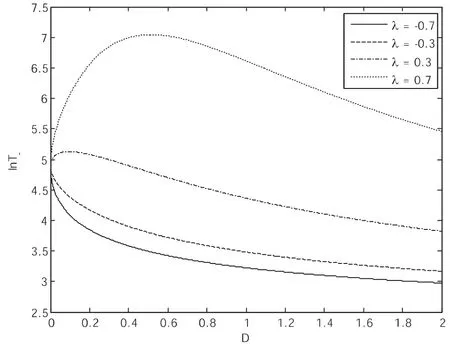
图2 T-作为乘性噪声强度D的函数随着噪声关联强度λ变化的曲线
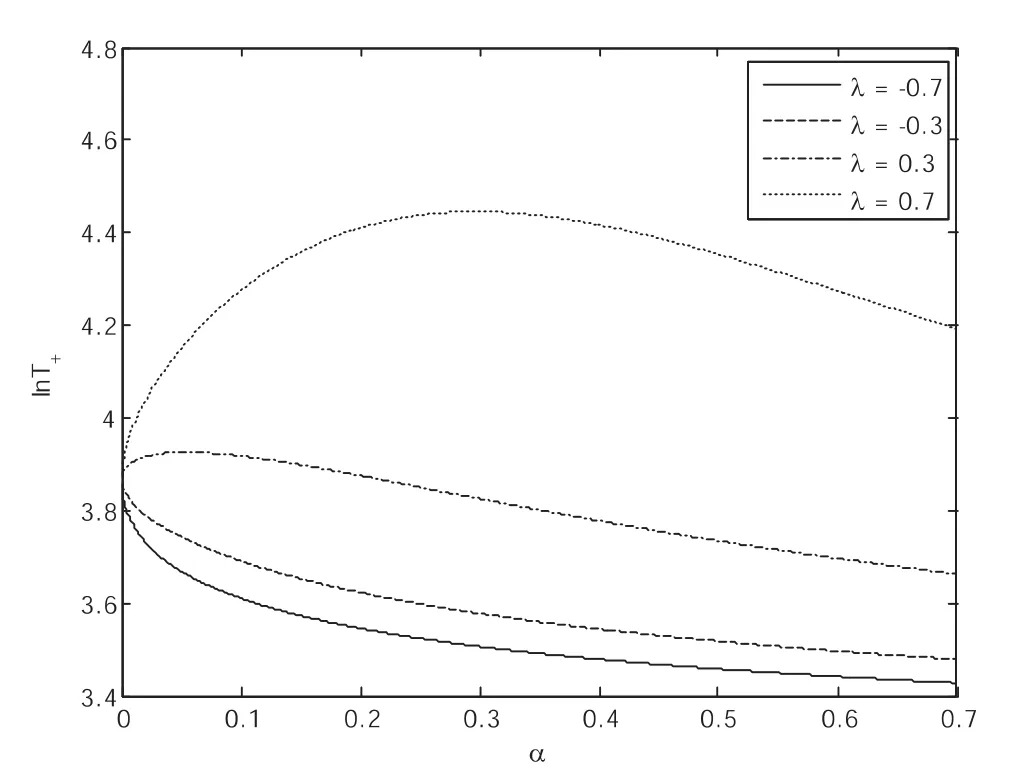
图3 T+作为加性噪声强度α的函数随着噪声关联强度λ变化的曲线
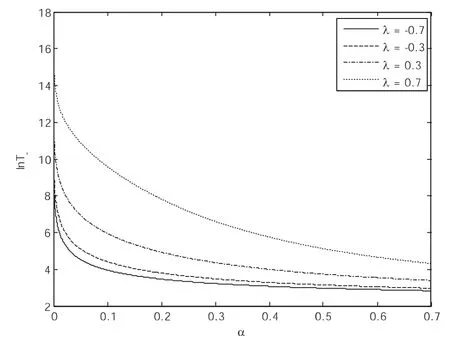
图4 T-作为加性噪声强度α的函数随着噪声关联强度λ变化的曲线
图3与图4分别给出了平均首次穿越时间T+与T-作为加性噪声强度α的函数随着不同的噪声互关联强度λ变化的曲线.从两图可以看出,当噪声互关联强度取值为负时(λ=-0.7,-0.3),加性噪声强度对两个方向的平均首次穿越时间Τ+与T-的影响是类似的,都随着α增加单调减小;而当噪声互关联强度取值为正时(λ=0.3,0.7),两图曲线有显著不同:T+随着加性噪声强度的增加先增加再减小,出现共振现象,此时系统稳定性增强;而T-曲线随着加性噪声强度的增加是单调减小的.
本文考虑了白关联高斯噪声与非高斯噪声对捕食食饵模型的影响.通过分析系统的平均首次穿越时间表达式,可得如下结论:乘性噪声强度与噪声互关联强度对两个方向的平均首次穿越时间T+和T-的影响是类似的;且当噪声互关联强度取值为正值时,两个方向的平均首次穿越时间曲线都出现了极大值,即共振现象.当噪声互关联强度取值为正时,加性噪声强度对两个方向平均首次穿越时间曲线的影响有显著不同,其中T+曲线出现极大值,而T-则随着加性噪声强度的增加单调减小.
〔1〕杨建华,刘先斌.色交叉关联噪声作用下癌细胞增长系统的平均首通时间[J].物理学报,2010,59 3727.
〔2〕Wang C J 2012 Acta. Phys. Sin. 61 010503.
〔3〕Fiasconaro A, Spagnolo B, Marcinek A O and Nowak E G 2006 Phys. Rev. E 74 041904.
〔4〕施锦,朱士群.虫口模型中的关联色噪声[J].苏州大学学报,2005,21 55.
〔5〕施锦.捕食-食饵模型中的随机共振[J].淮阴师范学院学报,2005,4 287.
〔6〕Fuentes M A, Tessone C J, Wio H S and Toral R 2003 Fluctuation and Noise Letter 3 L365.
〔7〕Bouzat S and Wio H S 2005 Physica A 351 69.
〔8〕Goswami G, Majee P, Ghosh P K and Bag B C 2007 Physica A 374 549.

