伴随置信度的线性回归模型

刘兆君

（山东工商学院数学与信息科学学院，山东烟台264005）



伴随置信度的线性回归模型

刘兆君

（山东工商学院数学与信息科学学院，山东烟台264005）

摘要：针对正态余项的线性回归模型，研究伴随置信度的线性回归模型。在一定概率下，设计随机变量以均值为中心的置信区间，建立机会约束规划，并在一定置信度下转化为确定性规划，应用LINGO 11优化软件求解，构造出伴随置信度的线性回归模型，实现对随机变量观测值信息的动态应用，可以实现伴随置信度的预测。实证分析表明，该模型可以依置信度不同程度地反映观测数据的多方面信息，选择最佳线性回归方程，更好满足需要。该模型有异于线性分位数回归模型的优点，丰富了线性回归分析的研究内容。

关键词：线性分位数回归模型；机会约束规划；线性回归方程；置信度；非线性规划

一、引 言

一般地，做统计数据分析比较常用的线性模型有传统的均值模型［1］391－415、最小一乘（线性中位数）回归模型［2］、线性分位数回归模型等［3－8］。为讨论问题方便，我们事先约定，所谓的传统均值模型是指随机余项是以零为均值的正态同方差分布，并且讨论中所有模型的因变量都是连续型随机变量。很明显，上述三种常用的线性模型，依据它们随机误差余项之间的关系，容易判定其有如下关系：从均值模型、最小一乘（线性中位数）回归模型到线性分位数回归模型是特例到一般的关系，即均值模型是最小一乘（线性中位数）回归模型的特例，最小一乘（线性中位数）回归模型是线性分位数回归模型的特例。尤其是以零均值正态同方差分布为随机误差余项的均值模型，由于正态分布为关于均值对称的分布，其均值与中位数相等，因此既可将其看成是均值模型，也可认为是线性中位数回归模型的特例，所以可以用最小一乘法研究均值模型，并且从这个意义上讲，最小二乘法也是研究特殊的线性中位数回归模型的一种方法。至此，我们关注的是上述三者关系链的两端，即均值模型与线性分位数回归模型的对比研究问题。实际上，线性分位数回归模型就是用一定累积概率下随机因变量取值的最大值来预测随机因变量的可能取值，由此设想，也可以用一定概率下随机因变量取值的均值来预测随机因变量的可能取值。事实上，按照均值中心论的思想，可以将随机变量的一组观测值，视为随机变量在其均值附近，在一定概率水平下取值的反映。因此，可以建立一定概率水平下的机会约束规划，并将它转化为一定置信度下的等价的确定性规划，运用LINGO 11优化软件编程求解，得到伴随一定置信度的线性回归方程，依置信度不同程度地反映随机变量的多方面信息，帮助我们从优、按需选择伴随置信度的线性回归方程，实现伴随置信度的预测，有利于科学决策。

二、伴随置信度的线性回归模型

设随机变量与一般变量之间的线性关系式为：其中x1，x2，…，xn为可以精确测量或可以控制的一般变量，Y是可观测其值的随机变量，a0，a1，…，an是未知参数，ε是不可观测其值的随机变量，假设ε ～N（0，σ2）。

为了估计的需要，做了m次独立观测试验，得到m组独立观测样本值：将上述样本值代入式（1）可得：其中ε1，ε2，…，εm相互独立，都服从N（0，σ2i），称为n元线性回归模型。

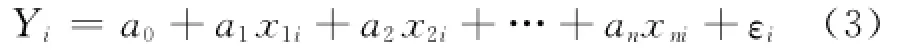
显然，式（3）的观测值是yi，i＝1，2，…，m。

本文的目的就是在给定置信度αi＜1下，利用观测样本值式（2），估计未知参数a0，

a1，…，an，σi，得到估计，确定n元线性回归方程：

称为伴随置信度α（0＜α＜1）的n元线性回归方程。给定概率αi，0＜αi＜1，由式（4）得：

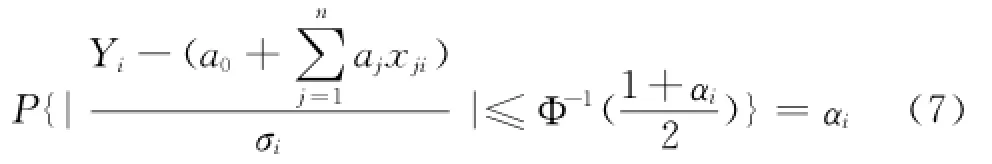
整理得：

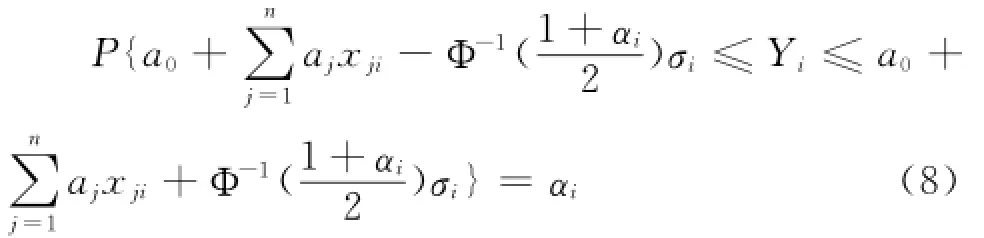
因此，对Yi的观测值yi，可以有置信度α下的确定性规划等价式：

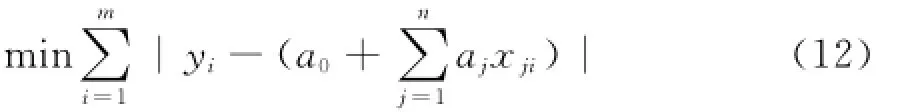
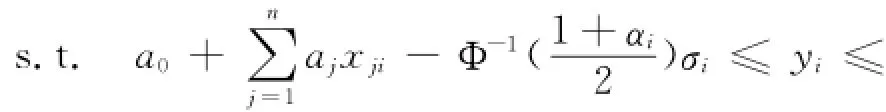
其中第一目标函数式（12），可转变为线性规划问题［9］，可以运用多目标加权化单目标法，求解上述多目标线性规划，应用LINGO 11优化软件，编程求解一个单目标线性规划，得到未知参数a0，a1，…，an，σi的估计值从而确立置信度为α的n元线性回归方程式（5）。

实际应用中，有时会出现诸αi或诸σi相等的情况，我们只须对式（9）～（11）以及式（12）～（14）进行适当调整即可。而当αi与σi同时相等时，如αi＝β，σi＝σ，为方便应用，仅对式（12）～（14）进行适当调整，有置信度α＝βm下的确定性规划等价式：

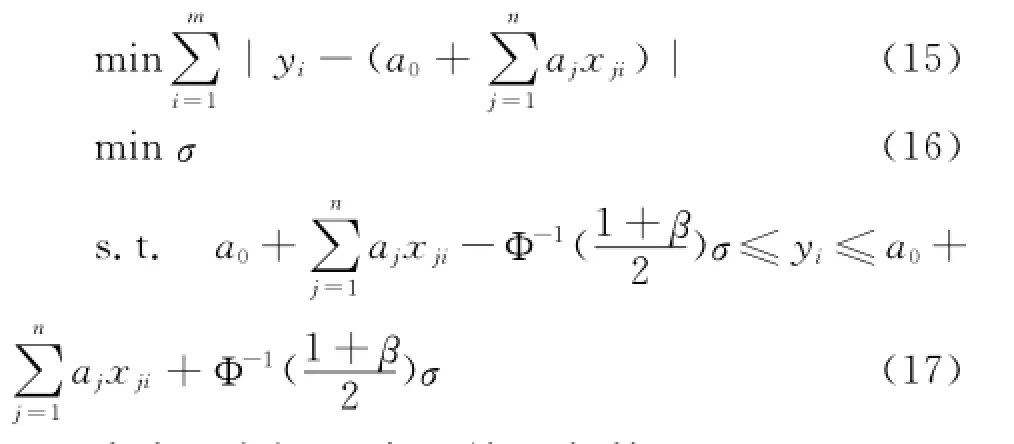
为实用方便，一般取诸αi相等。

三、实证分析

大气污染近年来为人们所关注，能够较科学地预测未来废气排放的情况，对治理大气污染至关重要。本文以某省工业废气排放量及各影响因素的统计数据（如表1所示）为依据［10］，建立该省工业废气排放量与各影响因素的伴随置信度的线性回归模型，更好满足实际需要。

表1　某省工业废气排放量及影响因子数据

假设y表示废气排放量，x1表示工业总产值，x2表示能耗，x3表示治理设备数。

设置信度α1＝0.9510，建立伴随置信度的线性回归模型：

εi～N（0，σ2），1≤i≤10，且相互独立，为求伴随置信度和回归模型，对于置信度为建立下列非线性规划模型：

minσ （20）

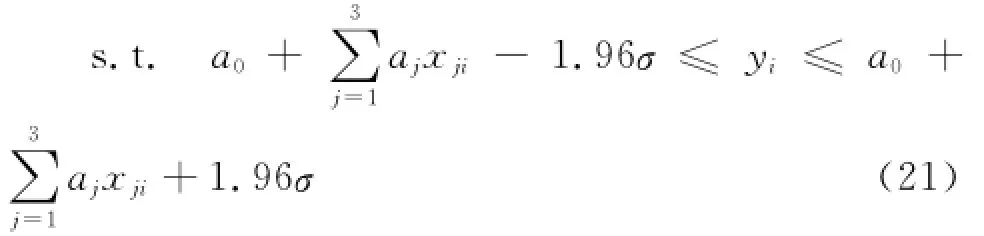
将表1中有关数据代入式（19）、（21），将两个单目标式（19）、（20）同取权重0.5，相加得单目标函数，并利用LINGO 11编程求解，可得：

得伴随置信度α1＝0.9510的线性回归方程：

由式（22）计算回归值的平均相对误差3.03%，结果如表2所示。

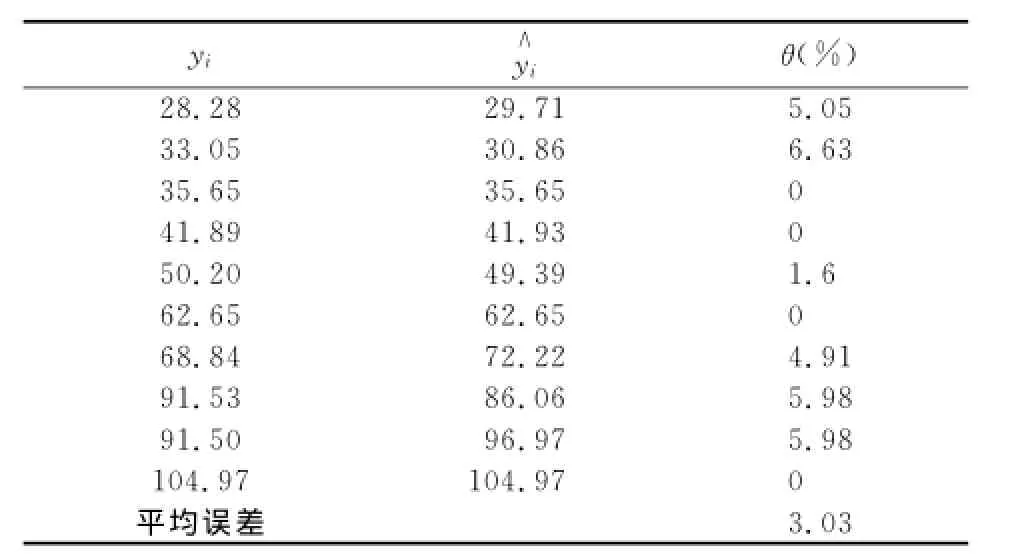
表2　伴随置信度α1＝0.9510的线性回归估计效果

同理，对于伴随置信度α2＝0.5010，α3＝0.7010，α4＝0.9010，也可以分别按上述过程求线性回归方程，分别为：

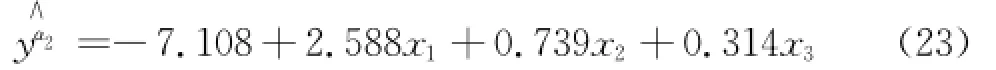
计算回归值，得到平均相对误差分别为3.05%、3.05%和3.03%，得到的σ估计值分别为7.947、5.248和3.328。

利用传统最小二乘法确定的线性回归方程为［10］：

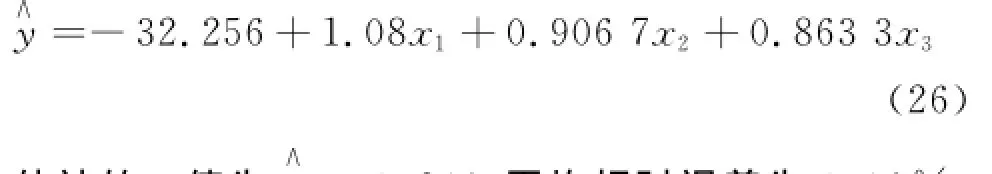
估计的σ值为σ＝3.246，平均相对误差为3.91%。

利用一般的最小一乘法确定的线性回归方程为：

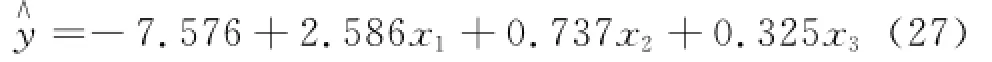
平均相对误差为3.04%。

经过简单对比可以发现，传统最小二乘法确定的线性回归方程式（26）和伴随置信度的线性回归方程式（22）、（23）、（24）与（25）相比，其预测效果明显较差，σ估计值比置信度α1＝0.9510估计的σ∧α1明显大，由此可以推测传统最小二乘法确定的线性回归方程的质量较差。一般的最小一乘法确定的线性回归方程式（27）的预测效果也略差于置信度α1＝0.9510的线性回归方程式（22）的预测效果，况且一般最小一乘法尚不具备方差估计及伴随置信度的功能。

从伴随不同置信度的线性回归方程的对比分析中可以发现，置信度增高，其线性回归方程的预测平均相对误差有变小趋势，预测效果趋好；置信度越高，因变量Y的根方差σ的估计值越小，其线性回归方程的预测稳定性越好。如果把平均相对误差与根方差σ做为评价线性回归方程的预测质量指标，则表明置信度增高，其线性回归方程的预测质量变好。

更重要的是，从伴随不同置信度的线性回归方程式（23）、（24）、（25）与（22）的对比分析中可以发现，随着置信度的提高，线性回归方程预测质量的提升，影响工业废气排放量的因素x1的系数逐渐变大，而因素x2与因素x3的系数却逐渐变小，这说明随着数据分析的逐渐深入、预测质量的提升，不同因素对工业废气排放量的影响作用越来越清楚地显现出来，因素x1的影响作用在提升，而因素x2与因素x3的影响作用在下降，因此因素x1的影响作用是主要的，而因素x2与因素x3的影响作用次之。这种动态实证分析过程不是一个线性回归方程所能比拟的，这就为我们控制工业废气排放量指明了方向，即在现有生产技术及废气治理技术条件下，因素x1工业总产值是控制的主要因素。

当然，实用中我们可以根据实际需要选用不同置信度的回归方程。最有意义的是清楚了所使用的线性回归方程及其预测结果的置信度，为科学决策提供了依据。

四、伴随置信度线性回归模型特性分析

很明显，机会约束规划式（9）、（10）和（11）的建立方法具有一般性，我们也可以按最小二乘法设立目标函数，建立机会约束规划。只是由于最小一乘法具有较好的稳健性，所以选择以最小一乘法建立机会约束规划。

伴随置信度的线性回归模型，是遵循以一定概率下随机因变量取值的均值，来预测随机因变量可能取值的研究思想得到的研究成果。伴随的置信度就是对线性回归模型及其以均值做为预测结果的不确定性风险的刻划。而线性分位数回归模型实质是研究利用一定累积概率下随机因变量取值的最大值来预测随机因变量的可能取值，虽然也具备一定的不确定性风险意义，但由于是累积概率，过于抽象，在实际应用中无法刻划具体预测的不确定性风险。因此，伴随置信度的线性回归模型中置信度的变化，一方面可以调整预测的效果，另一方面又可以调整预测值的可靠度；而线性分位数回归模型中概率的变化是为了全面刻划因变量分布的特征，得到较全面的分析结果［4］。这就是两种线性回归模型的区别，也是伴随置信度的线性回归模型的优点所在。

与传统的均值模型相比，伴随置信度的线性回归模型，除了具有能对预测结果的不确定性风险进行刻划的优点外，还具有借助不同置信度对随机观测值所含有的信息加以动态的不同程度利用的特点，通过伴随不同置信度的回归方程可知，由于不同程度的信息挖掘得到伴随不同风险的预测结果。

伴随置信度的线性回归模型，由于模型要求在一定置信度下，将随机变量所有观测值做为具有最小方差的正态分布的均值附近，因此适合分析的样本数据分布特征与传统的均值模型基本相同，一般适合样本数据比较集中、少有最好没有离群的异常点的数据，否则会导致回归方程向离群点的不良倾斜，影响预测的稳健性。

五、结 论

伴随置信度的线性回归模型，就是在一定置信度下，将随机变量所有观测值做为具有最小方差的正态分布的均值附近，依据此概率思想，按最小一乘法建立关于均值的机会约束规划，求得回归方程。因此，该模型具有最小一乘法估计的性质，即较好的稳健性、线性回归方程通过至少n＋1个样本点与渐近正态性。又由于该模型确定的线性回归方程是拥有最小方差的正态分布的均值，故此线性回归方程的预测效果较好，具有较好的预测稳定性。

参考文献：

［1］魏宗舒.概率论与数理统计教程［M］.北京：高等教育出版社，1983.

［2］陈希孺.最小一乘线性回归（下）［J］.数理统计与管理，1989（6）.

［3］陈建宝，丁军军.分位数回归技术综述［J］.统计与信息论坛，2008，23（3）.

［4］张涛.工资收入差异的解释：基于分位数回归的经验研究［J］.统计与信息论坛，2011，26（11）.

［5］姜励卿，钱文荣.公共部门与非公共部门工资差异的分位数回归分析［J］.统计研究，2012，29（1）.

［6］刘鑫，赵涛.基于分位数回归的天津市二氧化碳排放影响因素研究［J］.环境卫生工程，2014，22（1）.

［7］寿晖，张永安.基于分位数回归商业银行系统性风险研究［J］.技术经济与管理研究，2014（9）.

［8］张雨，刘倩，曾林蕊.生长曲线模型的分位数回归［J］.应用概率统计，2014，30（3）.

［9］王新宇，赵绍娟.基于分位数回归模型的沪深股市风险测量研究［J］.中国矿业大学学报，2008，37（3）.

［10］郑敏敏，肖秀钦，陈庆华，等，福建省工业废气排放量的因子分析与灰色预测［J］.环境科学与管理，2012，37（4）.

（责任编辑：崔国平）

【统计理论与方法】

Model of Linear Regression with Confidence Degree

LIU Zhao－jun
（School of Mathematics and Information Science，Shandong Institute of Business and Technology，Yantai 264005，China）

Abstract：For linear regression model with normal remainder，we studied linear regression model with confidencedegree.Underacertainprobability，bydesigningrandomvariablemean－centeredconfidenceinterval，book=7,ebook=8we set up a chance constrained programming，then turned it into a certain programming with a confidence degree and made use of Lingo11optimization software to solve the certain programming.At last we structured linear regression model with confidence degree and realized the dynamic application for random variable observed values information，we can predict with confidence degree.Empirical analysis shows the model can reflect in varying degrees on multifaceted information at observed data according to confidence degree and help us to select the best linear regression equation and better meet our needs.The model has the advantages of different from the linear quantile regression model，it enriches the content of linear regression analysis.

Key words：linear quantile regression model；chance constrained programming；linear regression equation；confidence degree；nonlinear programming

收稿日期：2015－02－26

文章编号：1007－3116（2015）07－0003－05

文献标志码：A

中图分类号：O212∶F222.3

作者简介：刘兆君，男，山东龙口人，教授，研究方向：不确定性的数学理论。